Top2Bary — a Complete Set of Routines
to Refer a Terrestrial Location
to the Solar System Barycenter
Pia Astone1, Kazimierz M. Borkowski2, Piotr Jaranowski3,
Andrzej Królak4 and Maciej Piętka3
1 Istituto Nazionale di Fisica Nucleare, (INFN)-Rome I, 00185 Rome, Italy
2 Centre for Astronomy, Nicolaus Copernicus University, Toruń, Poland
3 Institute of Theoretical Physics, University of Białystok, Białystok, Poland
4 Institute of Mathematics, Polish Academy of Sciences, Warsaw, Poland
-
Abstract:
This document describes a set of FORTRAN
procedures Top2Bary, worked out in the years 2000 to 2006 for
referencing of terrestrial astronomical observations to the Solar
System Barycenter in general and of data collected from the cryogenic
gravitational wave detector of the Roma group, named Explorer, in
particular. Algorithms employed, program structure and usage are detailed.
The referencing relies on calculation with very high precision
of the position and velocity of the observatory location at the time
of measurement with respect to the Earth barycenter and position
and velocity of this center with respect to Solar System
mass center as embodied in the JPL Planetary and Lunar Ephemerides,
DE405/LE405. These positions and velocities are expressed in the
rectangular equatorial coordinates of the ICRS, which correspond
to the reference frame defined by the equator and equinox of
the standard epoch of J2000.0. Presently the package is designed to
cover the period of 21 years beginning with 1990, the limits being set
solely by the time range of an ephemeris file compiled for the purpose.
1. Inroduction
The Gravitational Wave Detector (ROG) group at the National Institute
for Nuclear Physics - Frascati National Laboratories (INFN-LNF) has
constructed and operates resonant bar gravitational wave detector named
EXPLORER and located at CERN near Genova. The large amount of high
quality data have been collected and are being subjected to various
analyses. We have developed a set of analysis tools for an all-sky
search for continuous gravitational-wave signals in these data
(Astone et al. 2002, 2003, 2005).
This report describes algorithms and procedures incorporated into one
of the mentioned tools, the Top2Bary package or module. This set
of FORTRAN subroutines when called for given time and geographical
location returns corresponding vectors of position and velocity
of the location with respect to the Earth barycenter and of this
barycenter with respect to the Solar System Barycenter (SSB).
The sum of these vectors represent the location position and velocity
referred to the SSB. Thus Top2Bary is quite general
and as such could be used for a variety of other scientific purposes.
The Top2Bary has been developed initially by April 2001 (version 1.0)
and subsequently improved considerably through removal of bugs and by
introducing a few more subtle corrections (such as the Celestial Ephemeris
Pole offsets and the correction to the Equation of Equinoxes).
While the first version of this set has been created in Poland, our Italian
part have developed similar but completely independent tool, the
PSS_astro package (Astone 2003), based on the
NOVAS package (Kaplan 1989).
A comparison of outputs from both these tools allowed us to fix their bugs
with the result that differences now remain at the level of round-off
errors.
Furthermore, making extensive use of the SOFA package (Wallace 2004) we have
ad hoc composed yet two programs (T2C2kA and T2C2kB, see
Appendix), based on a new International Astronomical Union (IAU)
nutation-precession theory and reference
systems officially implemented in astronomy and space geodesy since 2003
(Capitaine et al. 2002, McCarthy & Petit 2003, Borkowski 2003, Wallace
2004), with the purpose of checking our geocentric outputs against those
obtainable from the best and most recent theories and algorithms available.
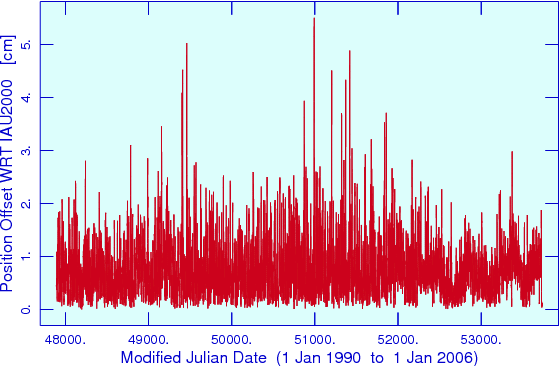
We have found that our rectangular celestial coordinates
are in agreement with the new system below 3 cm level in each coordinate and
6 cm in absolute position displacement (Fig. 1). These offsets
correspond to 1 to 2 mas (milliarcseconds) in spherical coordinates.
This good agreement could have been achieved only after supplementing our
packages with such fine corrections as for the celestial pole offsets and
the equation of equinoxes. The mentioned 6 cm satisfactorily compare with
the accuracy inherent in interpolated positions of the JPL ephemerides,
which is said to be not worse than 1 to 25 m or (for inner planets) 1 mas.
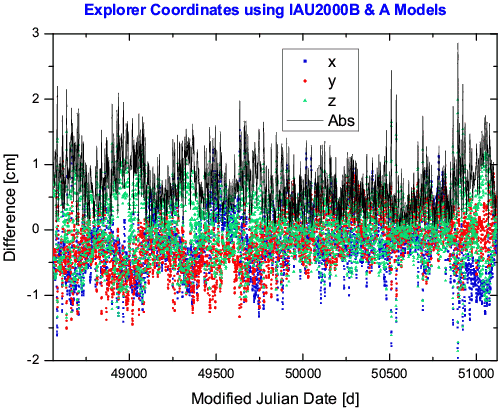
We note also that the new simplified IAU theory of nutation,
NU2000B, seems to be of the same order of accuracy (see Fig. 3).
|
Fig. 1.
Absolute difference between the Explorer location referred to the
geocentric ICRF computed with two packages: the Top2Bary and
T2C2kA, the latter incorporating full precision software based
on the 1997-2000 IAU astronomical reference systems, time scales, and Earth
rotation models. The data plotted were sampled every 14 UTC hours over
16 years (10019 points starting at MJD = 47892.0). The differences
in x, y and z coordinate over 1990.0 – 2006.0 averaged to 0.07, –0.14 and
0.00 cm, respectively, with overall rms of only 0.96 cm and the global absolute
maximum of 5.50 cm at MJD = 50991.8333 (to get these estimates a denser set
of 70130 samples spaced 2 hours has been generated and analysed).
|
The present version 2.1 of the Top2Bary is that of January 2006, and
from the user point of view differs from the version 2.0 (of February 2005)
only in that the user has now a few options easily settable in an auxiliary
file and the location position can be supplied directly in rectangular
coordinates (thus independent of the Earth ellipsoid parameters).
2. Overview of transformations involved
Introductory remarks on reference systems and frames
These remarks are based on most recent recommendations of IAU (Kaplan 2005).
Reference data for positional astronomy, such as the data in barycentric planetary
ephemerides, are now specified within the International
Celestial Reference System (ICRS). The ICRS is a coordinate system whose
origin is at the solar system barycenter and whose axis directions are effectively
defined by the adopted coordinates of 212 extragalactic radio sources which are
assumed to have no observable intrinsic angular motions. Thus, the ICRS is
a “space-fixed” system (more precisely, a kinematically non-rotating system) without
an associated epoch. However, the ICRS closely matches the conventional dynamical
system defined by the Earth’s mean equator and equinox of J2000.0; the alignment
difference is at the 0.02 arcsecond level, negligible for many applications.
The list of radio source positions that define ICRS for practical purposes is
called the International Celestial Reference Frame (ICRF).
The position and velocity 3-vectors taken from the JPL DE405/LE405
ephemeris are in equatorial rectangular coordinates referred
to the solar system barycenter. The reference frame for the DE405
is the ICRF; the alignment onto this frame, and therefore onto the ICRS,
has an estimated accuracy of a few milliarcseconds, at least for
the inner-planet data.
The DE405 was developed using Teph,
a barycentric coordinate time (Standish 1998). Teph is rigorously
equivalent to Barycentric Coordinate Time (TCB) in a mathematical
sense, differing only in rate: the rate of Teph matches the average
rate of TT (Terrestrial Time, or TDT), while the rate of TCB is defined
by the SI system. The IAU time scale, Barycentric Dynamical Time
(TDB), often (but erroneously) considered to be the same as Teph,
is a quantity that cannot be physically realized, due to its flawed
definition. So, in fact, the use of the name TDB actually refers to
quantities based on or created with Teph (because of this,
the IAU Working Group on Nomenclature for Fundamental Astronomy
has recommended changing the definition of TDB to be consistent
with that of Teph).
Astronomical constants obtained from ephemerides based on Teph
(or TDB) are not in the SI system of units and must therefore be scaled
for use with TCB or other SI-based time scales.
J2000.0 is the epoch 2000 January 1, 12h TT (JD 2451545.0 TT)
at the geocenter (“J2000.0 system” is shorthand for the celestial
reference system defined by the mean dynamical equator and equinox
of J2000.0.). The coordinate system defined by the “equator and equinox
of J2000.0”, can be thought of as either barycentric or geocentric.
It is also worth noting that the recent IAU resolutions do not describe
the proper reference system of the observer – the local, or topocentric,
system in which most measurements are actually taken. The resolutions
as adopted apply specifically to Einstein's theory of gravity, i.e.,
the general theory of relativity.
Time scales
It is assumed that the time, associated with observational data we are
dealing with, is the Coordinated Universal Time (UTC)
as disseminated by international time services. The UTC scale since 1972
is essentially uniform, except for occasional 1 second steps (leap seconds)
introduced internationally to compensate for the variable
Earth rotation. By 1 January 2006 there were 33 leap seconds. Earlier,
1961 to 1971, the adjustments were continuous. UTC devoid of these
adjustments is called the International Atomic Time, TAI. The TAI - UTC
differences are available in
tabular form.
Our tai_ut function reads similar file
and returns the difference calculated for given UTC Julian Date.
So, this difference added to UTC converts it to TAI which is uniform.
TAI in turn differs from the Terrestrial (Dynamical) Time, TDT or TT
(normally used to describe celestial phenomena by astronomers),
only by a constant term:
In principle, the time argument of the JPL positions and
velocities of celestial objects is Teph or the barycentric coordinate
time. This time scale in practice can be equated with the Barycentric
Dynamical Time, TDB (in spite of already noted inadequacy in definition).
The TDB differs from the TDT only by small periodic terms, which to
sufficient accuracy are usually simplified to only two largest terms:
|
TDB - TDT = 0.001658sin(g) + 0.000014sin(2g) seconds, |
|
where g = 357.53 + 0.9856003 (JD - 2451545.0) degrees
and JD is the Julian Date equal to MJD + 2400000.5, MJD being the Modified
Julian Date. So essentially, for many practical purposes, the two scales
do not have to be distinguished and could be assumed equal, TDB = TDT
(this possibility can be made effective in our procedures by setting the
iTDB option, in the useTop2B.cfg configuration file, to 0).
One can thus relate given UTC with barycentric positions of all the
major celestial bodies of the Solar System as obtainable from the JPL
ephemeris. These relations are
incorporated into the Top2Bpv subroutine, which also calls
the tai_ut function that reads a file with the UTC adjustments.
However, to relate the position of a point on the Earth to the geocentric
ICRF (i.e. the same frame as the barycentric ICRF except for the origin
of axes which is now at the barycenter of the Earth)
one has to use yet another time scale — the rotational time scale UT1,
which is nonuniform and is determined from astronomical observations.
The difference UT1 - UTC, the value of which is
presently maintained by international services within
±0.90 s, is taken from the IERS tabulations
of daily values available as eopc04.yy files,
where yy stands for a two digit year number (e.g. 99
for 1999, and 06 for 2006), at the
IERS Internet site.
The UTC to UT1 conversion takes
place in the sitePV subroutine, which calls a polar motion routine,
polmot. The latter returns the UT1 - UTC difference
interpolated (between nearest midnight values read from proper eopc04
file) to the UTC given, along with other Earth axis motion parameters
(terrestrial and celestial pole offsets) similarly interpolated. The UT1 time
can be readily converted to the Earth rotational angle or the sidereal time.
This last conversion is made in the sid function, which is a function
of UT1 and the location geographical longitude corrected for the polar motion.
Location coordinates and velocities with respect to Earth barycenter
To be able to express coordinates of a point on the Earth surface in
the Earth centered ICRF it is necessary to know orientation of
the Earth in space.
The primary effects that should be taken into account are: diurnal
(variable) rotation, precession and nutation of the Earth rotational
axis and polar motion. The precession is accounted for by applying
standard astronomical theories. We use the
new1 IAU theory
(Lieske 1979). The nutation could be also computed basing on a theory,
but the DE405 has it in numerical form, so we just read the nutation
angles, Dy and De.
These nutation angles are not the same as defined
in the newest IAU nutation theory, so when highest
precision is required the celestial pole offsets,
dy and de,
must also be added to these angles (in the past the magnitude of these
offsets remained below 0.1 arcsecond). For past years, since 1962, these
two offsets are included in the already mentioned eopc04.yy files.
The remaining two effects, the Earth variable
rotation and polar motion, are unpredictable for a longer
future, so also observational data must be used. The data necessary for
reduction are taken from the eopc04.yy files as well.
The polar motion can be taken into account by modifying the conventional
geographical coordinates of a point on the Earth (see Eqs. 5.1 in
Astone et al., 2002) or rectangular coordinates corresponding
to these conventional geographical coordinates:
where fo is the conventional geographical latitude,
lo – the conventional longitude,
h – the height above the Earth ellipsoid,
y = arctan(b tanfo /a)
– the reduced latitude,
ro = a cosy + h cosfo is the equatorial
component of the radius vector, and a = 6378.140 km and
b = a(1 - 1/f) are the semiaxes of the ellipsoid
(here the flattening f is taken equal to 298.257 or
1/0.00335281, which are the IAU or NOVAS value, respectively).
We have adopted the latter possibility using the following relations:
where Px and Py are the IERS coordinates of the pole,
with respect to the Conventional International Origin (to which
the 'conventional' geographical coordinates refer), converted to radians.
These (x,y,z) coordinates are expressed in the terrestrial reference
frame with the x axis directed toward the Greenwich meridian. To relate
them to the celestial frame, the ICRF, the rotational angle of the Earth
must be taken into account. This is done through conversion of UTC to UT1
(as described in the preceding section). The UT1 serves to calculate
the apparent (or true)
local sidereal time q
(returned by the sid function), which
includes the nutational component (nutation in longitude corrected for the
corresponding IERS celestial pole offset also taken from the IERS eopc04
files). With respect to the mean Greenwich sidereal time the apparent local
time is advanced by the true location longitude (calculated as l = arctan(y/x) with proper choice of one of the four quadrants) and the mentioned
nutational component. This component is equal to the so called equation of
equinoxes (Dy
+ dy) cose plus a very
small correction to this equation (which amounts to less than
0.003˘˘ and depends on the mean
longitude of the ascending node of the Moon). Our configuration file allows
the user to neglect this small correction or even use the mean sidereal time
instead. So computed local sidereal time is finally used to find rectangular
coordinates of the location in the IERS celestial reference frame:
where re = Ö{x2 + y2}
is the equatorial component.
At this point the location velocity due to Earth rotation can be
computed. The location motion relative to
the Earth barycenter is represented by a vector of constant length
(in principle vo = 2pre
per sidereal day = Wre)
and directed always towards the East in the topocentric reference frame.
This diurnal velocity vector has the following Cartesian components:
| |
|
|
vocos(q + p/2) = -vosinq, |
| |
| |
|
|
vosin(q + p/2) = +vocosq, |
| | (4) |
| |
|
| |
|
where the numerical value of vo in our program is
calculated with the NOVAS constant of the Earth angular rotation speed,
W = 2p/(sidereal day in
TAI seconds) = 7.2921151467×10-5
rad/s. This constant corresponds to NOmega (a parameter listed
in the configuration file) set to 1, and can be changed to the IERS
value of 7.292115×10-5 (NOmega =
0) or to 2p/(24×3600)×1.002737909350795 =
7.2921158553×10-5 (NOmega = 2).
All the above conversions are done in the sitePV subroutine,
whose listing is given below.
subroutine sitePV(sCJD,Xlat,Ylong,Zheigh,xyz)
c This subroutine calculates Cartesian coordinates and velocity of an
c observer at given geographical location with respect to the Earth
c barycenter in the reference frame of date |sCJD| (and not J2000.0).
c sCJD - (signed) Julian Date (UTC time scale)
c Xlat, Ylong, Zheigh - geodetic coordinates (rad) and altitude (m);
c if sCJD<0, these are the Cartesian coordinates Xlat=X, Ylong=Y, Zheigh=Z (km)
c xyz - 6-vector of Earth-centered rectangular coordinates (km) and velocity (km/s)
c Subroutines called:
c polmot(CJD,Px,Py,UT1_C,dpsi,deps) - returns polar motion, offsets and UT1-UTC
c sid(dj1,along) - calculates local sidereal time (apparent or mean)
implicit real*8 (a-h,o-z)
dimension xyz(6)
data a,frec/6378.140d0,298.257d0/,pi/3.141592653589793d0/
common /options/ iUT1_C,iPM,iTDB,NutSid,NutRem,NovF,NOmega,iSunV
common /nuta/ pnut(4)
CJD = dabs(sCJD)
c If appropriate, convert geographical to rectangular coordinates
if(sCJD.gt.0d0) then ! angular coordinates given
deg = pi/180d0
b = a - a/frec
if(NovF.eq.1) b = a - a*0.00335281d0 ! NOVAS value
psi = datan(b*dtan(Xlat*deg)/a)
ro = a*dcos(psi) + Zheigh*1d-3*dcos(Xlat*deg)
along = Ylong*deg
zo = b*dsin(psi) + Zheigh*1d-3*dsin(Xlat*deg)
xo = ro*dcos(along)
yo = ro*dsin(along)
else ! Cartesian coordinates given
xo = Xlat
yo = Ylong
zo = Zheigh
endif
c Polar motion data: Px,Py, UT1 - UTC and pole offsets interpolated from EOPC04.yy
call polmot(CJD,Px,Py,UT1_C,ddpsi,ddeps)
if(NutSid.eq.2) then ! add celestial pole offsets
pnut(1) = pnut(1) + ddpsi*pi/(3600*180)
pnut(2) = pnut(2) + ddeps*pi/(3600*180)
endif
conv=1d0/206264.8062470964D0
c Cancel out the Earth orientation parameters, if requested
if(iUT1_C.eq.0) UT1_C = 0
if(iPM.eq.0) conv = 0
Px = Px*conv
Py = Py*conv
c Compute observer's vectors with respect to Earth barycenter;
C wobble rotation follows
x = xo - Px*zo
y = yo + Py*zo
zo = zo + Px*xo - Py*yo
ro = dsqrt(x*x + y*y)
along = datan2(y,x) ! longitude corrected for polar motion
dj1 = CJD + UT1_C/86400d0 ! 'Rotational' Julian Date
alst = sid(dj1,along) ! local sidereal time
xyz(1) = ro*dcos(alst) ! Site position X component
xyz(2) = ro*dsin(alst) ! Site position Y component
xyz(3) = zo ! Site position Z component
vo = ro*7.292115d-5 ! mean Earth rotation rate (IERS 1992/2000)
if(NOmega.eq.1) vo = ro*7.2921151467d-5 ! NOVAS value [rad/s]
if(NOmega.eq.2) vo = 2*pi*ro/(24*3600)*1.002737909350795d0 != ro*7.2921158553d-5
xyz(4) = -vo*dsin(alst) ! Site velocity Vx component
xyz(5) = +vo*dcos(alst) ! Site velocity Vy component
xyz(6) = 0d0 ! Site velocity Vz component
end |
Since our approach is essentially classical these Cartesian coordinates
(X,Y,Z) and velocities (Vx,Vy,Vz)
are naturally referred to the frame of equator and equinox of date.
Therefore they are further nutated and precessed (in this order) back to
the standard epoch J2000.0, and this is performed in the
Top2Bpv subroutine by calling
the RemNut and prexyz procedures, separately for
the position vector and velocity vector.
Barycentric coordinates of the Earth (JPL ephemeris)
For computing the coordinates of the Earth barycenter, relative to
the Solar System barycenter, use is made of the fundamental Solar System
ephemerides from the Jet Propulsion Laboratory (JPL).
The latest JPL Planetary and Lunar Ephemerides, "DE405/LE405" or
just "DE405", were created in 1997 and are described in detail by
Standish (1998). They represent an improvement over their predecessor,
DE403, and are available via the Internet
(anonymous ftp) or on CDrom (from the publisher:
Willmann-Bell, Inc.).
As mentioned, the DE405 ephemeris is based upon the ICRF
(an earlier popular ephemeris DE200, which has been the basis of
the Astronomical Almanac since 1984, is within 0.01 arcseconds
of the ICRF frame).
It constitutes of a set of Chebyshev polynomials fit with
full precision to a numerical integration over 1600 AD to 2200 AD.
Over this interval the interpolating accuracy is no worse than 25
meters for any planet and no worse than 1 meter for the Moon.
The JPL package allows a professional user to obtain the rectangular
coordinates of the Sun, Moon, and nine major planets anywhere
between JED (i.e. Julian Ephemeris Date) 2305424.50 (1599 DEC 09) to
JED 2525008.50 (2201 FEB 20).
Besides coordinates it includes nutations and librations. Our routines
do make use of the JPL nutation in longitude and in obliquity after
correction for (addition of) the IERS celestial pole offsets.
In the application described in this document we have used only
a 21-year (1990 to 2010) subset of the original ephemeris.
The ephemeris gives separately the position and velocity of the
Earth-Moon
barycenter and the Moon's position and velocity relative to this barycenter.
The Earth position and velocity vectors are thus calculated as a fraction
(involving the masses of the two bodies) of the Moon's ones and opposite
to the latter. For example, the x-coordinate of Earth barycenter with
respect to the SSB is obtained as:
|
xEarth = xEM - xM/82.30056, |
|
where EM and M subscripts refer to the Earth-Moon barycenter
and the Moon, respectively, and the numerical denominator is equal to
the Earth-plus-Moon to Moon ratio of masses taken from the JPL ephemeris.
Since the DE405/LE405 coordinates are given in the J2000.0 reference frame
the position and velocity of the Earth barycenter so obtained need
not be nutated nor precessed.
Finally, the velocity vector of the Sun motion towards its apex (with
the speed of 20 km/s) can be optionally added to the Earth barycenter
velocity. The direction of solar
apex is assumed at 18h in right ascension and 30o
in declination in the frame of equator and equinox of J1900.0. Therefore this
direction is first precessed from that epoch to J2000.0. Since catalogue
sky positions in astronomy are not corrected for the apex motion this component
is actually only optionally included in the presented programs
(corresponding iSunV option is set to 0 in the code). If desired,
the iSunV option can be changed by the user just by setting
a nonzero value in the configuration file, useTop2B.cfg. In this
case the velocity vector towards the apex is added to the Earth velocity
vector (position remaining unaffected).
The position and velocity vectors of the Earth are computed
by calling the EarthPV subroutine, which in turn calls
the original JPL STATE routine slightly modified for our needs.
This subroutine reads and interpolates the JPL planetary ephemeris file
named DE405'90.'10.
3. The Top2Bary module
The described algorithms were implemented in an easily callable
subroutine package or module named Top2Bary consisting of
about 900 lines of FORTRAN code.
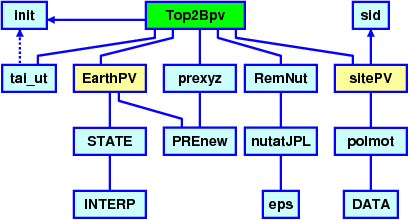
The module consists of the following subprograms:
Top2Bpv — main subroutine
init — sets some constants and parameters
sitePV — computes location geocentric vectors
EarthPV — computes Earth barycentric vectors
STATE — modified JPL STATE that reads the DE405
INTERP — original JPL subprogram
prexyz — precesses rectangular coordinates using PREnew
PREnew — computes general precession (the new IAU
theory1)
RemNut — eliminates nutation from rectangular equatorial vector
nutatJPL — returns JPL nutation angles and the mean obliquity
eps — calculates the mean obliquity
sid — computes local sidereal time (mean or apparent)
tai_ut — calculates the difference of TAI - UTC
polmot — interpolates IERS UT1 - UTC and offsets of poles
DATA — finds Gregorian or Julian calendar date from the JD number
|
|
Fig. 2. Block diagram of the
Top2Bary module |
The overall structure of the module is shown in Fig. 2.
The module expects the presence of the following data files:
-
DE405'90.'10 — JPL DE405 ephemeris file spanning 1990 to 2010 (binary)
tai-utc.dat — TAI - UTC table (ASCII)
eopc04.yy — IERS files, one per yy-year, for desired years (ASCII)
useTop2B.cfg — optional configuration file (ASCII)
Except for the last file which is looked for in the current directory, all
the other files must be placed in the /Top2Bary/EphData subdirectory.
All the ASCII files MUST be formatted in Windows style (i.e. the lines
must be terminated with CR/LF) and not UNIX style with LFs only. This is
important for a user who updates or modifies existing files or downloads
new eopc04.yy files from the IERS site, where they are stored in
the UNIX format.
The user is expected to append whole the Top2Bary code to his program
and call the Top2Bpv subroutine only, although, of course, he is free
to call any subprogram function or subroutine of the package as well. The source
code of this main procedure is reproduced verbatim below. A calling program must
avoid opening of devices (for reading or printing) with the logical numbers
11, 12, 15 and 16 which are used within the Top2Bary module by procedures tai_ut, STATE, polmot and init, respectively.
subroutine Top2Bpv(sCJD,clat,clong,height,pve,pvo)
c Procedure to calculate position (km) and velocity (km/s) of an observatory
c located at given geographical position (conventional coordinates in degrees
c and height above an Earth ellipsoid in meters, or corresponding Cartesian
c coordinates) at given Julian Date. It requires a JPL ephemeris file plus
c IERS time and Earth rotation data files.
c Argument description:
c sCJD - signed Julian Date representing the Coordinated Universal Time
c If sCJD is negative it signifies rectangular coordinates x,y,z below
c clat - observatory conventional geographical latitude (deg), or x (km)
c clong - observatory conventional geographical longitude (deg), or y (km)
c height- observatory height above the Earth ellipsoid (m), or z (km)
c pvo - 6 element array (3 elements for position vector in km, and 3 for
c velocity, km/s) of the observatory relative to Earth barycenter
c pve - 6 element array (3 elements for position vector in km, and 3 for
c velocity, km/s) of the Earth barycenter relative to Solar System Barycenter
c Subroutines and functions called:
c init - sets a few parameters and constants
c tai_ut(CJD) - returns the TAI - UTC difference
c sitePV(CJD,glat,glong,height_km,oxyz) - returns site vectors of date (CJD epoch)
c earthPV(TDB_JD,pve) - returns JPL Earth barycenter vectors (ICRF)
c RemNut(TDB_JD,pvo) - nutates a 3-vector from CJD back to J2000.0
c prexyz(TDB_JD,2451545d0,pvo) - precesses a 3-vector back to J2000.0
implicit real*8 (a-h,o-z)
double precision pvo(6),pve(6)
common /options/ iUT1_C,iPM,iTDB,NutSid,NutRem,NovF,NOmega,iSunV
data ifirst,pi/0,3.141592653589793d0/
if(ifirst.eq.0) call init
ifirst = ifirst + 1
CJD = dabs(sCJD)
EJD = CJD + (tai_ut(CJD) + 32.184d0)/86400d0
TDB = EJD
if(iTDB.eq.0) go to 6 ! No conversion to barycentric time
c TDB = TT + 0.001658 sin(g) + 0.000014 sin(2g) seconds, where
c g = 357.53 + 0.9856003 (JD - 2451545.0) degrees and JD is the Julian Date.
g = (357.53d0 + 0.9856003d0*(CJD - 2451545.d0))*pi/180
TDB_EJD = (0.001658*dsin(g) + 0.000014*dsin(2*g))/86400d0
TDB = EJD + TDB_EJD
6 call earthPV(TDB,pve) ! Earth SSB position & velocity (J2000.0 frame)
c Get observer's Cartesian coordinates and velocity (frame of date, UTC)
call sitePV(sCJD,clat,clong,height,pvo)
c Rotate these vectors to the J2000.0 frame (nutate and precess)
if(NutRem.ne.0) then
call RemNut(TDB,pvo) ! remove nutation from position
call RemNut(TDB,pvo(4)) ! remove nutation from velocity
endif
call prexyz(TDB,2451545d0,pvo) ! precess position to J2000.0
call prexyz(TDB,2451545d0,pvo(4)) ! precess velocity to J2000.0
end
|
On the first call this subroutine calls the init one where certain
parameters and constants are defined (either these coded there explicitely
or read from the useTop2B.cfg file described in the following
section). The ephemeris files required by the module,
i.e. DE405'90.'10 (if not changed by the user), tai-utc.dat
and yearly eopc04.yy, must be kept in the directory
\Top2Bary\EphData on the current disk.
4. Configuration file
If in the root directory of a program using the Top2Bary module
there is a file named useTop2B.cfg the init subroutine
opens it and reads some parameters therefrom. The file that originally
comes with the module has the following selfexplanatory content:
This is configuration file for the Top2Bary module.
These first four lines contain comments only. Each of the 8 following lines
start with a 1-digit parameter being read by the init subroutine. The second
column below shows data assumed by the module when it cannot find this file.
1 1 iPM 0/1 without/with polar motion
1 1 iUT1_C 0/1 without/with UTC to UT1 conversion
1 1 iTDB 0/1 without/with TDT to TDB conv. when calling JPL ephem.
2 2 NutSid 0/1/2 mean/apparent sid. time/+IERS corrections (CEP,EqEq)
1 1 NutRem 0/1 without/with nutation of calculated vectors
1 1 NovF 0/1 without/with NOVAS Earth flattening factor
1 1 NOmega 0/1/2 IERS/NOVAS/my mean Earth rotation speed
0 0 iSunV 0/1 without/with solar motion towards apex
DE405'90.'10 binary JPL ephemeris file (originally: DE405'90.'10)
|
If the user decides on using predefined settings, he may remove this file
altogether or, equivalently, rename it to e.g. NEVERuseTop2B.cfg.
5. Two practical examples
SSB2Det program
The program presented here has been used to generate coordinates
and velocities required for searches of the Explorer data described
in Astone et al. (2003 and 2005). During compilation
(we have used the Lahey Compiler LF90) the main module, which is
the subject matter of this document, is appended to this
small program, as specified in the last line.
Program SSB2Det
c Modifications to the version of June 13, 2000:
c Oct. 5, 2005: added storing obliquity value in the file epsilon.dat
c Jan. 15, 2006: enabled direct use of rectangular site coordinates
c USAGE: ssb2det MJD,clat,clong,height,step,N
c Special usage: ssb2det -MJD, x, y, z, step, N
c where the command line arguments are:
c MJD - (signed) Modified Julian Date (UTC based) of the first sample;
c if MJD is negative it signifies rectangular coordinates x,y,z (see below)
c clat - site conventional geodetic latitude (deg), or x (km)
c clong - site geographical longitude, East positive (deg), or y (km)
c height - site height above the Earth ellipsoid (m), or z (km)
c step - sampling interval (s)
c N - number of samples
c The program returns four vectors for each sample in four separate files
c (in units of km for positions and km/s for velocities):
c 1. Position vector of the location relative to the Earth barycenter
c 2. Position vector of the Earth barycenter relative to the SSB
c 3. Velocity vector of the location relative to the Earth barycenter
c 4. Velocity vector of the Earth barycenter relative to the SSB
c ascribed to disk devices as the logical units 1 to 4, respectively.
c In a separate file the true obliquity in radians is saved
implicit real*8 (a-h,o-z)
real*8 pvo(6),pve(6) ! arrays for site (pvo) and Earth (pve) vectors
character cline*127 ! max 127 characters for command line arguments
call getcl(cline)
if(cline.eq.' ') then
print*,' No command line arguments given. Running a test ...'
c cline=' 48002.0123456789, 53.1,18.55, 127, 7200.9001,25'
cline='-48002.0123456789, 3638.473270,1220.947798,5077.337129,'//
& ' 7200.9001,25' ! equivalently with rectangular site coordinates
endif
read(cline,*) sMJD,clat,clong,height,step,N
UTCJD0 = 2400000.5d0 + dabs(sMJD) ! UTC Julian Date of first sample
TDTJD0 = UTCJD0 + (tai_ut(UTCJD0) + 32.184d0)/86400d0 ! TDT/TT JD
open(1,file='rDet.dat')
open(2,file='rSSB.dat')
open(3,file='vDet.dat')
open(4,file='vSSB.dat')
open(5,file='epsilon.dat')
do 1 i = 0, N-1
UTCoff = i*step/86400d0
sCJD=dsign(UTCJD0 + UTCoff,sMJD)
call Top2Bpv(sCJD,clat,clong,height,pve,pvo)
write(1,'(3f13.6)') (pvo(j),j=1,3)
write(2,'(3f16.3)') (pve(j),j=1,3)
write(3,'(3f10.6)') (pvo(j),j=4,6)
write(4,'(3f11.6)') (pve(j),j=4,6)
call nutatJPL(TDTJD0 + UTCoff,dpsi,deps,eps)
write(5,'(1x,f11.9)') eps + deps
1 continue
end
include '\Top2Bary\Top2B\Top2Bary.for' ! append the module
|
The program executable SSB2Det.exe can be called by the user
(or another application) with arguments explained in comments of the program
itself (see source code printout above). When run without the command line
arguments, it assumes values specified in the code itself so that the generated
output files can be used as a check of proper functioning of the module.
Each of these test files has 25 rows and 3 columns (corresponding
to x, y and z components of a vector), except epsilon.dat
which is one-column file. For convenience of the user their content
is reproduced here in full.
rDet.dat rSSB.dat
-2370.863732 -3021.495059 5075.246433 -129159430.774 -70544670.345 -30593308.915
-537.331241 -3800.569169 5076.958017 -129052968.952 -70714470.051 -30666939.416
1439.726282 -3555.536358 5078.769834 -128946244.113 -70884127.158 -30740508.024
3027.590156 -2352.420792 5080.193682 -128839256.472 -71053641.303 -30814014.579
3798.410052 -515.402274 5080.845909 -128732006.243 -71223012.127 -30887458.920
3544.488337 1460.534056 5080.550786 -128624493.644 -71392239.268 -30960840.889
2334.244294 3042.971616 5079.387847 -128516718.892 -71561322.364 -31034160.325
493.778532 3805.522174 5077.670463 -128408682.206 -71730261.054 -31107417.066
-1480.994958 3542.716287 5075.861388 -128300383.807 -71899054.976 -31180610.955
-3057.972903 2325.367067 5074.448079 -128191823.914 -72067703.768 -31253741.829
-3812.238159 481.489600 5073.811345 -128083002.752 -72236207.068 -31326809.528
-3540.553738 -1492.082837 5074.122744 -127973920.542 -72404564.513 -31399813.893
-2316.125091 -3063.570583 5075.298359 -127864577.511 -72572775.740 -31472754.762
-468.874852 -3809.535862 5077.021417 -127754973.883 -72740840.389 -31545631.975
1503.454916 -3528.978132 5078.827644 -127645109.886 -72908758.095 -31618445.372
3069.419410 -2297.493750 5080.230362 -127534985.748 -73076528.496 -31691194.792
3807.069070 -446.906540 5080.851624 -127424601.699 -73244151.228 -31763880.073
3517.644005 1524.142279 5080.524043 -127313957.970 -73411625.931 -31836501.057
2279.129876 3084.553044 5079.335893 -127203054.792 -73578952.239 -31909057.582
425.244656 3813.872637 5077.607318 -127091892.400 -73746129.791 -31981549.488
-1544.481760 3515.585687 5075.804070 -126980471.030 -73913158.222 -32053976.613
-3099.306063 2270.065688 5074.412013 -126868790.915 -74080037.172 -32126338.799
-3820.280424 412.918317 5073.806217 -126756852.294 -74246766.275 -32198635.883
-3513.138094 -1555.447571 5074.149897 -126644655.407 -74413345.170 -32270867.707
-2260.638656 -3104.655266 5075.350444 -126532200.494 -74579773.493 -32343034.110
vDet.dat vSSB.dat epsilon.dat
0.220342 -0.172545 0.000208 14.766243 -23.590229 -10.229470 0.409146859
0.277153 -0.038842 0.000256 14.802784 -23.570451 -10.220886 0.409146865
0.259285 0.105327 0.000235 14.839294 -23.550623 -10.212280 0.409146870
0.171553 0.221116 0.000151 14.875775 -23.530745 -10.203651 0.409146875
0.037595 0.277325 0.000026 14.912226 -23.510817 -10.195001 0.409146879
-0.106492 0.258809 -0.000106 14.948647 -23.490838 -10.186328 0.409146882
-0.221885 0.170557 -0.000209 14.985037 -23.470809 -10.177633 0.409146884
-0.277491 0.036348 -0.000256 15.021397 -23.450730 -10.168915 0.409146886
-0.258327 -0.107655 -0.000234 15.057726 -23.430601 -10.160175 0.409146887
-0.169557 -0.222650 -0.000149 15.094025 -23.410421 -10.151413 0.409146887
-0.035099 -0.277652 -0.000024 15.130292 -23.390192 -10.142629 0.409146886
0.108816 -0.257841 0.000108 15.166529 -23.369911 -10.133823 0.409146885
0.223411 -0.168554 0.000211 15.202734 -23.349581 -10.124994 0.409146882
0.277807 -0.033850 0.000257 15.238907 -23.329200 -10.116143 0.409146878
0.257349 0.109974 0.000233 15.275050 -23.308769 -10.107269 0.409146874
0.167547 0.224166 0.000147 15.311160 -23.288287 -10.098373 0.409146868
0.032600 0.277957 0.000021 15.347238 -23.267755 -10.089455 0.409146862
-0.111131 0.256851 -0.000110 15.383284 -23.247172 -10.080515 0.409146854
-0.224918 0.166538 -0.000212 15.419298 -23.226539 -10.071552 0.409146846
-0.278100 0.031350 -0.000257 15.455279 -23.205856 -10.062567 0.409146836
-0.256349 -0.112285 -0.000232 15.491228 -23.185122 -10.053560 0.409146825
-0.165524 -0.225664 -0.000145 15.527143 -23.164338 -10.044531 0.409146814
-0.030099 -0.278239 -0.000019 15.563026 -23.143504 -10.035479 0.409146801
0.113436 -0.255841 0.000112 15.598875 -23.122619 -10.026405 0.409146787
0.226406 -0.164508 0.000213 15.634691 -23.101684 -10.017309 0.409146772 |
Orb program
Here we present another application, that we have used just for check-up of less
accurate data describing the Earth orbit in space. The executable Orb.exe
generates rectangular coordinates of the Earth center of mass with
respect to the SSB (JPL DE405 frame, thus ICRF) according to user
specifications in the command line or in response to a program prompt.
Results of computations
are written to a file (with the name composed of 'Orb' and the Modified
Julian Date value of the first sample rounded to three decimal places)
in a 4-column table. The table colums contain the time offset
(relative to the first sample) in TAI/UTC days and the three Cartesian
coordinates of the Earth expressed in astronomical units (AU). The source
program listing below includes a numerical example of input arguments and
the resulting output.
Program Orb ! computes coordinates of Earth wrt SSB
c USAGE: Orb MJD,step,N
c where the command line arguments are as follows:
c MJD - Modified Julian Date (UTC based) of the first sample
c step - sampling interval [UTC/TAI seconds]
c N - number of samples
c The program returns rectangular coordinates of the Earth (in AU) referred to SSB
c (frame: ICRF or J2000.0) in a file 'orb00000.000' where zeroes stand for MJD;
c the first column of the file gives time offset in days for each sample
implicit real*8 (a-h,o-z)
real*8 MJD,pve(6),pvo(6)
character cline*127,outfil*12
data AU/0.1495978706910d+09/,clat,clong,height/0d0,0d0,0d0/
call getcl(cline)
if(cline.eq.' ') then
print*,' No command line arguments given. Type-in MJD,step,N: '
read(*,*) MJD,step,N
write(cline,*) MJD,step,N
print*,' Input data: '//cline(1:65)
endif
read(cline,*) MJD,step,N
write(outfil,'(a,f9.3)') 'Orb',MJD
open(1,file=outfil)
do 1 j = 0, N-1
T = j*step/86400d0
call Top2Bpv(2400000.5d0 + MJD + T,clat,clong,height,pve,pvo)
1 write(1,'(f14.9,3f19.15,3f11.4)') T,(pve(k)/AU,k=1,3) ! position
c & ,(pve(k)/AU*1d5*86400d0,k=4,6) ! velocity in 1E-5 AU/d (for AA test)
print'(a,a,f12.5,a,i6)',' Output in the file "'//outfil,
& '" step [s] =',step,' N =',N
end
include '\Top2Bary\Top2B\Top2Bary.for'
c Test example
c Input (typed on prompt or in command line): 48580.790850744, 86400, 3
c Content of the output file "Orb48580.791":
c 0.000000000 0.524712484382844 0.771327942103784 0.334341141730002
c 1.000000000 0.509759571077188 0.779499088435775 0.337884390296571
c 2.000000000 0.494651799591344 0.787432883266874 0.341324852639191
|
6. New in version 2.2
The Modified Julian Date based on UTC does not allow to set uniquely the time
of a leap second since it would be numerically indistinguishable from the time
of the second immediately following it. To have a way to generate data also
within the leap second one can revert to using the MJD based on TT (TDT) time
instead of UTC as an input argument. This possibility has been implemented
in Top2Bary, v. 2.2. It requred to considerably modify the tai_ut
subprogram in order that it is able to accept also JD(TT) as its input argument
and to detect moments when the JD falls within the range of a leap second.
For the user to work with MJD(TT) he just advances the value of iTDB
option in useTop2B.cfg file by 2 (to make it 2 or 3,
depending on previous value).
The usual UTC based MJD can be converted to TT based MJD with the formula:
MJD(TT) = MJD(UTC) + (TAI – UTC + 32.184)/86400,
where the TAI – UTC difference (since 1972 it is an integer number of TAI seconds)
can be taken from our tai-utc.dat file (remembering that within the leap
second itself the difference is the same as prior to it). E.g., the most recently
introduced leap second at the end of 2005 begins at MJD = 53736.0 and lasts till
another numerically the same MJD but 1 UTC/TAI second later. Since TAI – UTC in 2005
equalled to 32 s, these two moments expressed in ET equal to 53736 + 64.184/86400 and
53736 + 65.184/86400 at the beginning and end of the leap second, respectively.
The new option allows for direct comparison of certain computations with
data in astronomical yearbooks (which frequently contain ephemerides, whose
argument is the ephemeris time ET, which is equivalent or close to TDT, or TT,
or Teph). As an example, having set iTDB = 3, we have used
the Orb (with the line following the label 1 there
uncommented to have velocities as well) supplying the following input data:
53004, 864000, 3, which mean requesting starting date of
January 0, 2004 (i.e. December 31, 2003), at 0.0 hours of TT, step of 10 round
days, and generating 3 samples. The output, lines here interleaved with
the corresponding data taken from the Astronomical Almanac for the year
2004 (AA), looks like this:
Earth position in AU wrt SSB (Day,X,Y,Z) at 0h TT (T_eph in AA)
0.000000000 -0.147440491730541 0.888923036138659 0.385320984472414
Jan 0 AA: -0.147440492 0.888923036 0.385320984
10.000000000 -0.316918997408260 0.850456482944105 0.368637656795466
Jan 10 AA: -0.316918997 0.850456483 0.368637657
20.000000000 -0.476535025262845 0.785575371003839 0.340512466873750
Jan 20 AA: -0.476535025 0.785575371 0.340512467
|
As expected, our positional data agree exactly with those published in
the AA. Likewise, the corresponding velocities (in 10–5
AU/d) turned out to be numerically identical with those of the AA,
where they are printed in the same format:
Day X_dot Y_dot Z_dot
0 -1727.5341 -248.0625 -107.6159
10 -1653.6985 -519.1662 -225.0970
20 -1530.1763 -775.5049 -336.1788
|
|
___________________________ |
Appendix: T2C2kA module implementing the new IAU2000 system
Modules T2C2k serve to transform position and velocity vectors
from terrestrial to celestial geocentric frame of reference according
to most recent developments in the field.
subroutine T2C2k(CJD,clat,clong,height,pvo) ! the 'A' variety
c Main subroutine for transformation of site coordinates from the terrestrial
c (ITRF) to celestial (ICRF) reference frame according to the new IAU algorithms.
c It returnes position (km) and velocity (km/s) of an observatory located
c at given geographical position (conventional coordinates in degrees and
c height above the Earth ellipsoid in m) at given Julian Date (UTC).
c Performs similar job as does Top2Bpv described in the main text except that
c no Earth barycenter vectors wrt SSB are computed.
c Argument description:
c CJD - Julian Date representing the Coordinated Universal Time
c clat - observatory conventional geographical latitude (deg)
c clong - observatory conventional geographical longitude (deg)
c height- observatory height above the Earth ellipsoid (m)
c pvo - 6-element array (3 elements for position vector in km, and 3 elements
c for velocity, km/s) of the observatory relative to Earth barycenter
implicit real*8 (a-h,o-z)
double precision pvo(6),xyz(6),RPOM(3,3),RBPN(3,3),RT2C(3,3)
common /options/ iUT1_C,iPM,iTDB,NutSid,NutRem,NovF,NOmega,iSunV
call DAT(CJD, tai_utc, J)
EJD = CJD +( tai_utc + 32.184d0)/86400d0
c Get interpolated Earth orientation and rotation data from EOPC04.yy file
call polmot(CJD,Px,Py,UT1_C,dpsi,deps)
c Convert or possibly neglect the Earth orientation parameters
conv = 1d0/206264.8062470964D0
if(iPM.eq.0) conv = 0
if(iUT1_C.eq.0) UT1_C = 0
Px = Px*conv
Py = Py*conv
c (step 1) Get the s' quantity
date1 = dint(EJD)
date2 = EJD - date1
SP = sp2000(DATE1,DATE2)
* DATE1,DATE2 d TT date (JD = DATE1+DATE2)
* SP2000 d the quantity s' in radians
c (step 2) Form the polar motion (wobble) matrix (given pole coord.)
call POM2000(Px, Py, SP, RPOM)
* Px,Py d coordinates of the pole (radians)
* SP d the quantity s' (radians)
* RPOM d(3,3) polar-motion matrix
c (step 3) Earth Rotation Angle (UT1 required)
UT1 = CJD + UT1_C/86400d0
DJ1 = dint(UT1)
DJ2 = UT1 - DJ1
ERA = ERA2000(DJ1, DJ2)
* DJ1,DJ2 d UT1 date (JD = DJ1 + DJ2)
call XYS2000A(DATE1, DATE2, X, Y, S)
* DATE1,DATE2 d TT as a 2-part Julian Date
* X,Y d Celestial Intermediate Pole
* S d the quantity s
c (step 4) Bias-precession-nutation matrix for intermediate system
c to GCRS transformation
call BPN2000(X, Y, S, RBPN)
* X,Y d CIP coordinates
* S d the quantity s (radians)
* RBPN d(3,3) intermediate-to-celestial matrix ("Q")
c (step 5) Compose final terrestrial to celestial system rotation matrix
c for the CEO-based transformation
call T2C2000(RPOM, ERA, RBPN, RT2C)
* RPOM d(3,3) polar motion matrix (W)
* ERA d Earth Rotation Angle (radians, giving matrix R)
* RBPN d(3,3) intermediate-to-celestial matrix (Q)
* RT2C d(3,3) returned terrestrial-to-celestial matrix
c (step 6) Get observer's xyz coordinates and velocities
deg = 180/3.141592653589793d0
along = clong/deg
alat = clat/deg
call OBSxyz(alat,along,height/1000d0,xyz)
c This routine returns (in xyz) conventional rectangular coordinates and velocity
c of site similarly as does sitePV of the Top2Bary but without accounting for
c polar motion and sidereal time (i.e. as if they were all equal to 0).
c (step 7) Rotate the xyz vectors according to the RT2C matrix (Sofa routine)
call iau_RXP(RT2C, xyz, pvo) ! position vector
call iau_RXP(RT2C, xyz(4), pvo(4)) ! velocity vector
return
end
c Other required subroutines appended to or INCLUDEd in the T2C2kA:
c subroutine OBSxyz(Xlat,Ylong,Zheigh,obs) - see above (modified sitePV)
c subroutine init - taken from Top2Bary
c subroutine data(JD,L,M,N,J1G0) - taken from Top2Bary
c subroutine polmot(dj,px,py,pUTC,pdpsi,pdeps) - taken from Top2Bary
c All the following subprograms come from the SOFA package (www.iau-sofa.rl.ac.uk):
c DOUBLE PRECISION FUNCTION ERA2000 ( DJ1, DJ2 ) - Earth Rotation Angle
c DOUBLE PRECISION FUNCTION SP2000 ( DATE1, DATE2 ) - s' quantity
c DOUBLE PRECISION FUNCTION iau_ANPM ( A ) - normalizes A to -pi <= A < +pi
c SUBROUTINE DAT ( CJD, DELTAT, J ) - this is iau_DAT modified by KMB
c (to have CJD as input instead of date +)
include '\Top2Bary\SOFA\SofaMatr.for' ! matrix calculus grouped in one file
include '\Top2Bary\SOFA\POM2000.f' ! Polar Motion matrix
include '\Top2Bary\SOFA\BPN2000.f' ! Bias+Precession+Nutation matrix
include '\Top2Bary\SOFA\XYS2000A.f' ! Celestial Intermediate Pole IAU2000
include '\Top2Bary\SOFA\T2C2000.f' ! Terrestrial to Celestial final matrix
|
As seen from the included partial listing of T2C2kA code, it is composed
of ready FORTRAN subprograms publicly available in the
SOFA package
and of a few subroutines adapted or adopted
from the Top2Bary module. Another variety of this program, T2C2kB
has similar structure but is built using the classical equator and equinox paradigm
(however in this case it is made entirely equivalent to the new paradigm, i.e.
using the new nutation-precession theory that does not require the subtle
corrections) and
employing the shorter nutation procedure (NU2000B.f, which is much faster
but also considerably less accurate than the one built into XYS2000A.f file).
|
|
Fig. 3.
Differences between Cartesian coordinates of the Explorer referred
to the geocentric ICRF as computed with two varieties of the T2C2k
corresponding to the IAU model 'B' (less accurate nutation algorithm, classical
equator and equinox approach) and 'A' (full precision, presented in this Appendix).
The dots represent differences
in x, y and z coordinate and the distance between the two positions is drawn
with the continuous line. The data plotted were sampled every 12 UTC hours over
7 years starting with MJD = 48561.0 (1 Nov 1991).
|
Acknowledgments:
The contributions of K.M. Borkowski, P. Jaranowski, A. Królak,
and M. Piętka were supported in part by the KBN (Polish State
Committee for Scientific Research) Grant No. 1 P03B 029 27.
REFERENCES
Astone P., 2003, PSS_astro User Guide
(see also PSS_astro_PG.pdf).
Astone P., Borkowski K.M., Jaranowski P., Królak A., 2002, Data
analysis of gravitational-wave signals from spinning neutron stars.
IV. An all-sky search, Phys. Rev. D, 65, 042003.
Astone P. et al., 2003, All-sky upper limit for gravitational
radiation from spinning neutron stars, Class. Quantum Grav., 20,
No 17 (7 September 2003), S665–S676.
Astone P. et al., 2005, An all-sky search of EXPLORER data,
Class. Quantum Grav., 22, No 18 (21 September 2005), S1243–S1254.
Borkowski K.M., 2003, Referring a Detector to the Solar System
Barycenter, Mathematics of Gravitation II, Warsaw, September 1 – 9, 2003.
Capitaine N. et al. (eds.), 2002, Proceedings of the IERS
Workshop on the Implementation of the New IAU Resolutions, Paris, 18 – 19
Apr. 2002, IERS Technical Note No. 29.
Kaplan G.H., 2005, The IAU Resolutions on Astronomical Reference Systems,
Time Scales, and Earth Rotation Models, USNO Circ. No. 179 (Oct. 20, 2005).
Kaplan G.H. et al., 1989, Mean and Apparent Place Computations
in the New IAU System. III. Apparent, Topocentric, and Astrometric Places
of Planets and Stars, Astron. J., 97, 1197 – 1210
(see also NOVAS info file).
Lieske J.H., 1979, Precession Matrix based on the IAU(1976) System
of Astronomical Constants, Astron. Astrophys., 73, 282 – 284.
McCarthy D. D., Petit G. (eds.), 2003, IERS Conventions (2003)
(or here),
IERS Tech. Note No 32
(Frankfurt: IERS Central Bureau).
Standish E.M., 1998, JPL Planetary and Lunar Ephemerides, DE405/LE405,
IOM 312.F-98-048.
Wallace P.T., 2004, SOFA software support for IAU 2000, American
Astronomical Society Meeting 204, #28.02, May 2004.
Report prepared in January 2006;
last modified: 2006 Feb. 16
Footnote:
1
The once adequate word 'new' is misleading in view of recent
revolutionary changes of concepts since by this name really referred
is here that old IAU 1976 theory (Lieske 1979).
File translated from TEX
by
TTH, version 3.72 on 2 Feb 2006.



