Scope of this presentation
-
• General intoduction to transformations between reference frames
• On the new paradigm officially implemented in astronomy and space
geodesy since 2003
Background
-
• Search for gravitational waves in data from the Explorer detector
(Królak et al., this Meeting; see also a dedicated
web page)
• Two programs developed independently, by Pia Astone and myself,
for the purpose of referring the data to an inertial frame
• Comparison of outputs from these programs allowed us to
correct flaws down to centimeter level (subsequently confirmed
by comparison with newest IAU/IERS software)
—— Transformations ——
Purpose
- To express the position and velocity
in a (quasi)inertial reference frame
by means of rotations, translations and
scalings
of coordinates and time
Frames
- Terrestrial (ITRF)
— pole and origin of longitudes
Celestial (ICRF)
— CEP/CIP and equinox/CEO
geocentric (GCRF) — Earth center of mass
barycentric (BCRF) — solar system barycenter
Transformation of coordinates
[EB] — a vector in the terrestrial frame (ITRF)
[SSB] — the same position/velocity in BCRF
[Terra] — the Earth position/velocity in BCRF
[SSB] = [Terra] + P·N·R·W·[EB]
— classical
[SSB] = [Terra] + BPNR·W'·[EB]
— new classical
[SSB] = [Terra] + BPNR'·W'·[EB]
— IAU2000
|
where we have the following time dependent matrices (Ri being
a rotation around i-th axis):
B = R3(dao)·R2(dx)·R1(-dh) — bias,
P — precession (4 or 5 rotations),
N — nutation (3 rotations),
R = R3(-GAST) — Earth diurnal rotation,
W = R1(-v)·R2(u)·R3(-s') — polar motion
(wobble),
BPNR' =
R3(E)·R2(d)·R3(q-E-s)
— new idea
-
E = arctan(Y/X) — 'intermediate right ascension' of the CIP,
d = arctan(Ö{X2+Y2}/Z)
— 'i. co-declination' of the CIP,
q — Earth rotation angle (ERA or stellar angle),
s/s' — describes current position of the CEO/TEO
Transformations of time
Classical:
UTC Û UT1 Û
UT1R Û GMST Û GAST
UTC Û TAI Û TDT/TT/ET
Û TDB
New:
UTC Û UT1 Û UT1S
Û ERA
UTC Û TAI Û
TT/Teph
Û TCG Û TCB
Effects to account for
Type
Diurnal Earth rotation
Precession
Nutation
Dy, De
corr.
eq. eqx. corr.
FCN
geodesic nutation
Polar motion
Leap second in UTC
UT1 – UTC
UT1S – UT1 (zonal tides)
UT1 corr. ocean tides
PM corr. tides < 1 d
Solid Earth tides
Polar tides
Plate motion
Local site displacements:
ocean loading
atmospheric loading
postglacial rebound
Site coordinates error
Earth
ephemeris (JPL)
TT – UTC (TDT – UT1)
TDB/TCB
– TDT/ET
Teph – TT
|
Magnitude
360 °/d
50 "/y
9 "
0.03 "
0.0027 "
0.001 "
0.00015 "
0.55 "
1 s
0.9 s
0.17 s
0.0001 s
0.001 "
<76 cm
25r ´ 7h mm
2 °/My
a few cm
0.9 mm/mbar
±0.01 ° = 36 "
±0.1–0.3 km/y
65 s (now)
0.0017 s
0 s
|
Displacement
6378 km
1500 m/y
280 m
0.9 m
8 cm
3 cm
0.5 cm
17 m
450 m
400 m
76 m
4.5 cm
3 cm
22 cm
2.6 cm
3 cm/y
3 cm
3 cm
1 cm/y
±1100 m
±1–5 km
2000 km
50 m
0 m
|
EM propagation effects
Atmospheric refraction
Diurnal aberration
Stellar aberration
Deflection of light
Refraction in the solar corona
Light time (planets)
|
35'
0.32"
20"
2"
negl.
D/c
|
—–Old vs. New Paradigm—–
Some properties
Old
FK5
Bright stars
Moving reference frame
Newtonian
CEP
Equinox (precessing)
IAU1976 precession
IAU1980 nutation
Sidereal time:
GAST = a + b·UT1 +
+ c·UT12 + d·UT13 +
+ Dy
cose + corr.
|
New
ICRS
Extragalactic sources
Fixed reference frame
Relativistic
CIP
CEO (stable)
IAU2000A/B
PN theory
Earth rotation angle:
q = a' + b'·UT1
|
|
Greenwich & CIO
TEO not defined
(u,v)
|
Greenwich & CIO
TEO on CIP equator
(u,v,s')
|
Gains
• Higher accuracy (marcseconds level)
• Simplified ideas and procedures
• Relativistic relation between BCRS and GCRS
• Reference frame is fixed — coordinates of defining
objects in ICRF essentially epoch independent
• The frame independent of the dynamics of the solar system
• Computer routines made readily available:
-- IERS Conventions 2000 site,
-- IAU SOFA
(Standards Of Fundamental Astronomy)
Problems
• Two paradigms coexisting in practice for long
• Complex practical procedures prepared by a few people
(e.g. GST – ERA relation published 2 month back has been derived
in 28 steps — will be difficult to check by independent parties)
• Delayed implementation (formally since 2003.0, Astron. Almanac
for 2005)
• IAU2000A precession-nutation theory overdue complex:
-- nearly 1400 terms down to 0.1 mas
-- absolute accuracy 0.2 ÷ tens of mas (FCN)
-- has errors (VLBI ® CIP offset, B matrix)
-- possible replacement by SF2001 PN theory (Shirai & Fukushima) with 194 terms
• IAU2000B oversimplified (77 terms, 1 mas;
Bangert)
• Terminology — numerous new terms and abbreviations (sometimes
inconsistent, e.g. ERA or stellar angle, NRO or CEO, or lack of friendly
names, e.g. s, s' quantities)
• Inadequately explained and popularised among common users; sources include:
-- IAU resolutions (IAU Inf. Bull. 88)
-- dispersed refereed papers
-- Proc.
IERS Workshop Implem. New IAU Resolutions (2002)
-- IERS Standards 1996
-- IERS
Conventions 2000 (to appear this fall)
-- Explanatory Supplement to the Astron. Almanac (2004?)
FCN component and the IAU2000 system
|
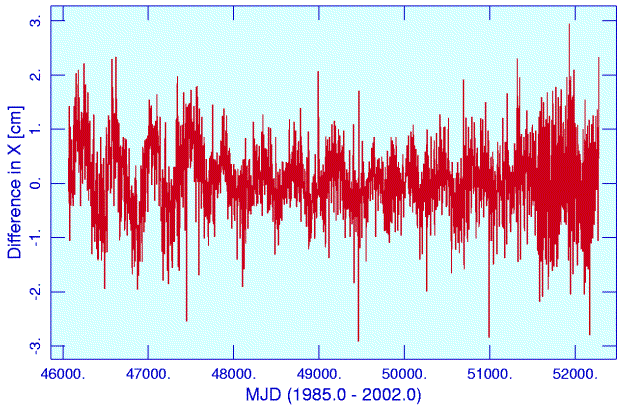
Differences in x coordinate of the EXPLORER detector position
transformed to ICRF with the classical and new IAU
procedures (data plotted every 1.7 days)
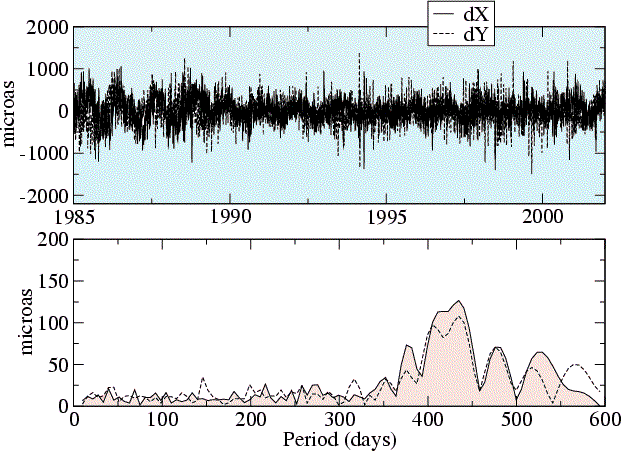
Differences between 'observed' X,Y of the CIP and
predicted values based on the IAU2000A developments (Capitaine
et al. 2003, A&A 400,1145–1154)
|
Acknowledgements
I would like to state with gratitude that the success of 'tuning'
my program to
the most up-to-date IAU/IERS standards has been possible owing to
cooperation with Dr Pia Astone of the Istituto Nazionale di Fisica Nucleare (Rome).
This study and programming work behind it were supported through
the Polish National Committee for Scientific Research (KBN)
Grant No. 2 P03B 094 17 managed by Prof. Andrzej Królak of the Institute of Mathematics, Polish Academy of Sciences (Warsaw).