|
|
|
| Interferometr, także ten wielkobazowy, jest filtrem częstości przestrzennych przepuszczającym selektywnie tylko określone struktury rozkładu jasności radioźródeł. Synteza apertury, czyli technika odtwarzania obrazów albo map radioźródeł, polega na formowaniu charakterystyki przenoszenia takiego filtru. Radioastronomowie uzyskują w ten sposób nowe narzędzie badawcze, które jest równoważne pojedynczemu teleskopowi o średnicy 10 000 km. |
Jeszcze do niedawna radiowe pomiary położeń źródeł na niebie nie dorównywały swą dokładnością tradycyjnej astrometrii optycznej, a wykonywano je głównie w celu identyfikacji optycznych odpowiedników radioźródeł. Obecnie pomiary takie radioastronomowie wykonują z precyzjami tysiąckrotnie lepszymi, niż ich koledzy posługujący się techniką optyczną. Przewrót ten odbił się oczywiście w innych dziedzinach, które zawsze były spokrewnione z astrometrią — geodezji, astronomii dynamicznej i testach teorii grawitacyjnych. Daleko zaawansowane są już prace nad przygotowaniem tak bardzo potrzebnego, niemal idealnie nieinercjalnego układu odniesienia opartego na radioźródłach pozagalaktycznych, praktycznie nieruchomych dla ziemskiego obserwatora (ze względu na ich olbrzymie odległości).
Obszar zastosowań radioastrometrii, bo tak przyjęto nazywać tę nową gałąź, rozciąga się dziś od najdalszych rejonów obserwowalnego Wszechświata do Ziemi, obejmując przy tym tak użytkowe dziedziny jak: nawigację, geodezję czy kartografię. W promieniowaniu widzialnym (na fotografiach) najodleglejsze obiekty, zwane kwazarami, przypominają zwyczajne słabe gwiazdy. Natomiast radiowe mapy kwazarów i radiogalaktyk wykonane z rozdzielczościami dziesięć lub więcej razy większymi ujawniają bogactwo struktur, zaskakującą zmienność i procesy angażujące niewyobrażalne ilości energii. Wśród około pięćdziesięciu dotychczas zbadanych tego typu obiektów, u siedmiu wykryto ekspansje materii z prędkościami ponadświetlnymi. To szokujące odkrycie można wytłumaczyć na gruncie mechaniki relatywistycznej jako efekt pozorny (są też zwolennicy realności prędkości ponadświetlnych,
 |
|
| Fot. 1. Ogólny widok toruńskiego radioteleskopu o średnicy 15 m |
A zaczęło się to wszystko 16 lat temu, kiedy niemal równocześnie w Kanadzie i w Stanach Zjednoczonych przeprowadzono pierwsze udane eksperymenty nowa techniką, zwaną w i e l k o b a z o w ą, zaś w literaturze naukowej i mowie potocznej częściej określaną akronimem VLBI (czyt. wi-el-bi-aj) — skrótem od ang. Very Long Baseline Interferometry. Dziś tego rodzaju obserwacje przeprowadza się regularnie (kilka kilkunastodniowych sesji w roku) w około 20 stacjach świata. Jedna z nich (dodajmy z pewnym zażenowaniem, że jest to jednocześnie najmniejsza w tym gronie stacja) znajduje się koło Torunia przy Uniwersytecie Mikołaja Kopernika i jest wyposażona w radioteleskop o średnicy 15 m.
Interferometr wielkobazowy odróżnia od konwencjonalnego w pierwszym rzędzie to, że jego elementy składowe pracują zupełnie niezależnie. W każdej ze stacji obserwacje są najpierw zapisywane na taśmie magnetycznej, a dopiero po pewnym czasie, potrzebnym na transport tych nośników informacji, są odtwarzane, synchronizowane i korelowane między sobą. Zapis niezależny usuwa konieczność budowania łącz pomiędzy punktami odbioru, które z różnych powodów nie rozwiązałyby i tak problemów w przypadku odległości większych niż kilkaset kilometrów. Technika VLBI ma też, niestety, cały szereg wad ograniczających powszechność jej stosowania. Do takich zalicza się m.in. konieczność używania w każdej stacji
 |
| Fot. 2. Toruński system odbiorczy VLBI na pasma 609 MHz i 5 GHz przygotowany do zamontowania w ognisku czaszy radioteleskopu. U góry tego urządzenia znajdują się właściwe anteny i ta strona zwrócona jest w kierunku czaszy w czasie użytkowania. Poniżej anten mieszczą się wzmacniacze, mieszacze, urządzenia zasilające, regulujące temperaturę i urządzenia diagnostyczne. Stąd sygnał przesyłany jest kablami do pobliskiego budynku, gdzie znajduje się reszta urządzeń do przetwarzania sygnału i sterowania teleskopem |
Proponujemy Czytelnikowi przyjrzenie się nieco dokładniej jednemu z warsztatów radioastronoma, korzystającego z techniki VLBI — syntezie apertury. Produkty z tego warsztatu — to mapy nieba o najwyższych osiąganych współcześnie rozdzielczościach kątowych sięgających 0,0001". Zauważmy, że o taki kąt zmieni się położenie zenitu obserwatora na powierzchni Ziemi, kiedy przesunie się on (obserwator) zaledwie o 3 mm!
Z praktyki wiemy, że antena w postaci krótkiego (w porównaniu do długości odbieranej fali λ) przewodu jest prawie bezkierunkowa, co objawia się tym, że słyszalność odbieranej stacji prawie nie zależy od ustawienia takiej anteny, a już w żadnym wypadku nie uda się nam zlokalizować kierunku, skąd nadchodzi odbierany sygnał. Mówimy wówczas, że rozdzielczość kierunkowa naszego systemu jest słaba albo prawie żadna. Kątową rozdzielczość teleskopu, tak optycznego jak i radiowego, wyznaczają liniowe rozmiary lub apertura instrumentu. Teleskop o średnicy czaszy, soczewki lub lustra równej D ma zdolność rozdzielczą około λ/D radianów (1 rad ≈ 200 000"). Duże teleskopy optyczne osiągają rozdzielczości przewyższające kilkaset razy możliwości nieuzbrojonego oka ludzkiego (około 3'), przy czym ich potencjalnie większe rozdzielczości ogranicza turbulentna atmosfera Ziemi. Na to, aby radioteleskop osiągnął rozdzielczość teleskopu optycznego (powiedzmy 1") musiałby mieć czaszę o średnicy niekiedy milion razy większej niż ten optyczny — dokładniej: tyle razy, ile razy dłuższa jest fala radiowa od optycznej. Łatwo jest obliczyć, że rozdzielczość 1" ma teleskop o średnicy około 200 000 λ, co dla fali o długości np. 10 cm (zakres radiowy) czyni już 20 km. Największy radioteleskop (w Arecibo) ma czaszę o średnicy zaledwie 300 m. Na szczęście, a stanie się to oczywiste nieco później, wzór, który podaliśmy na rozdzielczość teleskopów jest znacznie ogólniejszy i stosuje się do dość dowolnych układów teleskopów, a wielkość D interpretuje się wtedy jako największą odległość pomiędzy elementami danego układu.
Promieniowlnie elektromagnetyczne odległych źródeł kosmicznych dociera do Ziemi w postaci fal niemal płaskich. Jeśli oś parabolicznej czaszy skierowana jest na źródło, wszystkie promienie po odbiciu od czaszy wpadają do ogniska w punkcie 0 (rys. 1), przy czym ich drogi, licząc od czoła fali do ogniska, są jednakowe. Mówimy wtedy, że sygnały w ognisku dodają się z tą samą fazą, przez co ulegają wzmocnieniu. Jeśli jednak źródło znajdzie się pod kątem θ do osi teleskopu, to drogi promieni nie będą już jednakowe i na skraju czaszy ich różnica osiągnie wartość D·sinθ. Chwilowo ograniczymy się do dyskusji o tym przypadku (skraju czaszy), teleskop zaś pozbawiony całej powierzchni odbijającej z wyjątkiem dwóch fragmentów na przeciwległych skrajach czaszy będziemy nazywali interferometrem prostym (dwuelementowym) o bazie D (bazą jest właściwie wektor o tej długości i kierunku wyznaczonym przez elementy interferometru). Dla prostoty, także na pewien czas, zajmiemy się tylko przypadkiem dwuwymiarowym.
| Rys. 1. Ilustracja zasad działania radioastronomicznych systemów antenowych. Miejsca oznaczone literami A1 i A2 symbolizują powierzchnie zbierające sygnał. Mogą to być fragmenty czaszy paraboloidalnej, jak w zwykłym teleskopie, albo dowolnej konstrukcji anteny wyposażone w systemy odbiorcze, jak w przypadku interferometru. Sposób doprowadzenia sygnałów do miejsca korelacji (punkt O) wiąże się z typem instrumentu. W szczególności, w interferometrach połączonych na drogach A–O są łącza kablowe lub mikrofalowe, zaś w VLBI sygnały pokonują tę drogi najczęściej ... samolotami lub innymi środkami komunikacji w postaci zakodowanej na taśmach magnetowidowych. Interferometr dwuelementowy ma napięciową charakterystykę kierunkową typu sinusoidy (linia ciągła przy ognisku paraboli), zaś wypełniona do końca paraboloida — sumę wielu sinusoid odpowiadających składającym się na nią interferometrom (linia przerywana). Moc odbieranego promieniowania jest proporcjonalna do kwadratu charakterystyki napięciowej |
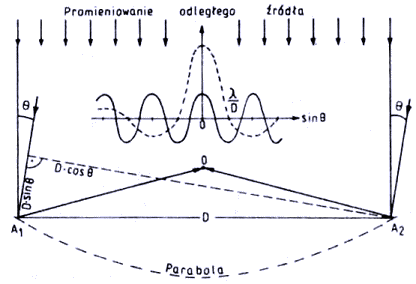 |
Przy pewnym kącie θ zdarzy się, że wyżej wspomniana różnica dróg promieni zrówna się z połową długości odbieranej fali, λ/2 i wówczas promienie te po zsumowaniu wygaszą się wzajemnie bez reszty tak, jak znikłyby na wodzie dwie fale o jednakowych amplitudach, których grzbiety jednej przypadałyby w tych samych miejscach, co doliny drugiej. Wprawdzie promieniowanie elektromagnetyczne naturalnych źródeł kosmicznych na ogół nijak nie przystaje do czystej sinusoidy — są to raczej fragmenty sinusoid o ciągle, i w sposób losowy, zmieniających się parametrach — ale efekt znoszenia się pozostaje dokładnie tak samo skuteczny, jeśli tylko względne opóźnienie dwóch jednakowych sygnałów losowych jest niewielkie, wtedy to obie repliki, w każdej chwili z osobna, można traktować jako czyste sinusoidy typu cosψ i cos(ψ + 2πD·sinθ), w których na ψ składa się przyczynek losowy i 2πft, gdzie f jest częstotliwością odbieranego sygnału, zaś t — czasem. Wypisane tutaj dwie funkcje możemy traktować jako uproszczony napięciowy model odbieranego sygnału. Moc rejestrowanego sygnału interferometru jest kwadratem sumy tych funkcji. Przy wzroście różnicy dróg o następne λ/2 sygnały ponownie dodadzą się w fazie i zaobserwujemy drugie maksimum ich mocy (napięciowo będzie to minimum). Widać już, że ze zmianą kąta na wyjściu prostego interferometru pojawia się sygnał zmodulowany sinusoidą z ekstremami (minimami i maksimami) tam, gdzie różnica dróg jest całkowitą wielokrotnością λ i z miejscami zerowymi przy nieparzystych wielokrotnościach λ/2. Te ekstrema to nic innego, jak znane z optyki prążki interferencyjne, w radioastronomii zwane listkami. Kilka z nich zilustrowano linią ciągłą na wykresie umieszczonym przy ognisku paraboli z rys. 1. Zauważmy, że listki interferencyjne są tutaj jednocześnie kierunkową (napięciową) charakterystyką czułości naszego interferometru, gdyż położenie listka wyznacza nam kierunek
 |
|
| Fot. 3. Sterownia toruńskiego teleskopu. W głębi widać cały zespół urządzeń elektronicznych związanych z wzmacnianiem, filtrowaniem, kodowaniem czy detekcją i zapisem odebranego sygnału. Znakomita większość tej aparatury została wykonana na miejscu, w Katedrze Radioastronomii UMK. W prawym stojaku, w jego środkowej części, znąjduje się bodajże najważniejsza część systemu do obserwacji techniką VLBI — formater. Kontrolę prowadzenia teleskopu wykonuje się obecnie za pomocą komputera M 400 (odpowiednika PDP 11/10), którego nie widać na zdjęciu |
Pouczające jest prześledzenie odpowiedzi interferometru prostego na źródło punktowe, tzn. o rozmiarach kątowych znacznie mniejszych od odstępu listków, oraz na źródło o prostokątnym (jednostajnym) rozkładzie jasności, o rozciągłości kątowej dokładnie równej odległości maksimów (a nie ekstremów) listków. W pierwszym przypadku, jak się domyślamy z poprzedzającej analizy, amplituda interferencji będzie równa całkowitej mocy źródła, a faza będzie zerowa (maksimum w zerze odpowiadającym kierunkowi źródła), w drugim zaś — listki interferencyjne w ogóle się nie pojawiją. Dzieje się tak dlatego, że każde dwa punkty źródła odległe o połowę odstępu maksimów generują niezależne listki interferencyjne o dokładnie przeciwnych (różniących się o π) fazach i jednakowych amplitudach, zatem znoszące się doskonale. Nasze źródło prostokątne zawiera tylko takie pary punktów, dlatego jest niewidoczne przez interferometr. Z tego samego powodu źródła jeszcze bardziej rozciągłe ujawniają się jako pozbawione tego znoszącego, się fragmentu o szerokości równej całkowitej wielokrotności odstępu maksimów listków charakterystyki kierunkowej.
Tak więc, w ogólniejszym przypadku obserwuje się jakiś ułamek całkowitej mocy źródła w postaci listków interferencyjnych o niezerowej fazie. Ten ułamek nazywa się w i d z i a l n o ś c i ą ź r ó d ł a, która w połączeniu z fazą stanowi tzw. funkcję widzialności. Amplituda i faza są podstawowymi obserwowalnymi wielkościami interferometrii, zawierającymi całą informację interesującą użytkownika interferometru.
Fakt, że prosty interferometr jest czuły tylko na pewne struktury źródła podsuwa myśl, że jest on rodzajem filtru. Rzeczywiście, z całej rozmaitości struktur źródła na odpowiedź interferometru składają się tylko te fragmenty, które wykazują okresowość wzdłuż kąta, tzn. w przestrzeni, równą odstępowi maksimów napięciowej charakterystyki kierunkowej interferometru (przypomnijmy, że wszystkie mniejsze źródła wykazują taką okresowość, ale istnieje ponadto wielka różnorodność źródeł większych mających też tę własność). W związku z tym mówi się, że ów przyrząd jest filtrem częstości przestrzennych. Częstość własną interferometru (tę przestrzenną) definiuje się zwykle jako składową bazy prostopadłą do kierunku źródła i wyraża w długościach fali odbieranego promieniowania: D·cosθ / λ.
Odwrotność tej wielkości, a więc długość fali przestrzennej, to wspomniana wcześniej kątowa zdolność rozdzielcza instrumentu. Ponieważ częstość własna interferometru jest funkcją kąta θ, to przy ustalonym położeniu bazy D nasz filtr ulega przestrajaniu w częstości w zakresie od zera (dla kąta θ = π/2) do D/λ (dla kąta θ = 0), gdy źródło wędruje po nieboskłonie, podążając za ruchem dziennym sfery niebieskiej. Po każdej zmianie kąta przepuszczane są przez ten filtr inne składowe struktury źródła. W ten sposób dokonuje się analiza widmowa źródła, a powstałe z pomiaru amplitudy i fazy listków widmo przestrzenne zawiera pełną informację o kształcie źródła, aż do struktur o wymiarach kątowych λ/D (wszystkie struktury mniejsze od λ/D będą nieodróżnialne od tych granicznych). W celu odtworzenia rozkładu jasności źródła wystarczy do widma zastosować operację odwrotną do przeprowadzonej analizy — syntezę obrazu. Mogłaby ona polegać na odtworzeniu wszystkich zmierzonych listków interferencyjnych z ich właściwymi amplitudami i fazami i prostym zsumowaniu powstałych sinusoid. Taka suma to już obraz albo rozkład jasności. Taki sam skutek osiąga się mniej czasochłonnym aparatem matematycznym, zwanym przekształceniem Fouriera. W uzupełnieniach do tego artykułu Czytelnik znajdzie nieco więcej informacji o analizie widmowej, obiektach tam spotykanych i stosowanej terminologii.
Widmo przestrzenne źródła można otrzymać niemal natychmiast, bez oczekiwania na znaczący obrót Ziemi, dysponując wieloma interferometrami o bazach pokrywających dostatecznie gęsto przedział od 0 do D, niekoniecznie na tym samym odcinku w przestrzeni. Procedura taka jest podstawą metody nazywanej s y n t e z ą a p e r t u r y, gdyż na końcowy wynik składa się szereg niezależnych obserwacji wykonanych przy użyciu niewielkich powierzchni zbierających (zwracamy uwagę dla jasności, że termin apertura używamy w dwóch znaczeniach: otwór względny, albo powierzchnia zbierająca i liniowe rozmiary). W odróżnieniu od tej, syntezę omówioną wcześniej a wykorzystującą obrót Ziemi nazywa się r o t a c y j n ą albo s u p e r s y n t e z ą. Specjalistyczne sieci anten do syntezy apertury zaprojektowane są do wykorzystania obu metod. Niektóre z kilku do kilkudziesięciu anten takich sieci umieszczone są na torowiskach. W celu wzbogacenia widma przestrzennego albo, co jest równoważne, pokrycia powierzchniami zbierającymi możliwie gęsto i równomiernie pewnego obszaru, obserwacje tego samego źródła lub wycinka nieba prowadzi się często przez wiele dni, codziennie z inną konfiguracją anten.
Wypełnijmy teraz resztę paraboli z rys. 1, tworząc wiele elementarnych interferometrów o równoległych i malejących do zera bazach oraz jednakowych powierzchniach zbierających. Realizujemy tym samym myślową syntezę apertury. Każdemu z tych interferometrów odpowiada inna częstość przestrzenna, a więc i inna charakterystyka kierunkowa. Suma częstości przestrzennych składa się na całe pasmo, czyniąc że nasza antena staje się dolnoprzepustowym filtrem pasmowym o równomiernej charakterystyce od 0 do D/λ. Charakterystyką kierunkową tego teleskopu jest suma elementarnych charakterystyk, czyli suma sinusoid, jakimi są listki interferencyjne poszczególnych interferometrów. W granicznym przypadku nieskończenie wielu elementarnych baz suma wspomnianych sinusoid wynosi: sin(πD/λsinθ) / (πsinθ).
Funkcję tę naszkicowano linią przerywaną na rys. 1 (ten sam przebieg zawierają w różnych skalach prawe strony rys. C i F w materiałach uzupełniających).
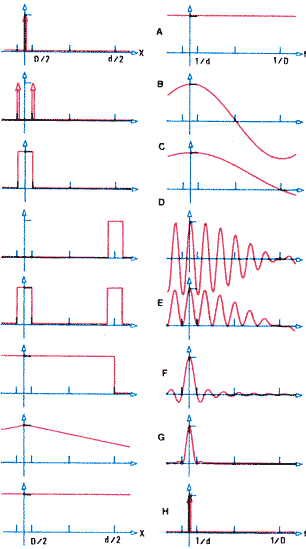
WIDMO I PRZEKSZTAŁCENIE FOURIERA
Faktem powszechnie znanym jest to, że funkcja okresowa, taka jak np. fala akustyczna związana z tonem wydobytym z instrumentu muzycznego, składa się z sinusoid o częstościach będących całkowitą wielokrotnością częstości podstawowej (odwrotności okresu funkcji), zwanych harmonikami. Podobnie jest z funkcjami nieokresowymi, które na ogół dają się wyrazić w postaci sumy wielu sinusoid typu a·cos(2πfx + φ) o różnych amplitudach (a), fazach φ i częstościach (f), już nie tylko harmonicznych. Widmem funkcji nazywa się rozkład amplitud i faz takich sinusoid w funkcji ich częstości. Analiza widmowa to proces rozkładu funkcji na sinusoidy w celu otrzymania widma. Jednym z aparatów matematycznych częściej utywanych do analizy widmowej jest przekształcenie Fouriera. Można zapytać, co się dostanie, obliczając widmo z widma? Otóż, z dokładnością do znaku fazy, transformatą Fouriera widma jest funkcja wyjściowa, dlatego funkcję i jej widmo nazywa się parą transformat Fouriera. Także stąd mówi się o dwoistej reprezentacji tej samej funkcji: bądź w dziedzinie czasu albo przestrzeni (u nas x i postać wyjściowa funkcji), bądź w dziedzinie częstosci rozumianych zwyczajnie, czasowo albo, tak jak w tym artykule, przestrzennie (f i widmo funkcji wyjsciowej). Kilka przykładów funkcji i ich transformat zawierają rysunki od A do H, przy tym Czytelnik może smiało zamienić miejscami osie x i f, tak jak to zrobiono z rysunkami A i H. Chociaż z koniecznosci ograniczyliśmy się tutaj do przypadków jednowymiarowych, to Czytelnik może z powodzeniem uogólnić te pojęcia na więcej wymiarów, przyporządkowuiąc każdemu wymiarowi w przestrzeni niezależną oś częstości przestrzennych
SPLOT I FILTRY
Czytelnikowi z pewnością nie jest obce wygładzenie przebiegów przez utworzenie średniej bieżącej. W takiej operacji każda liczba danego ciągu zastępowana jest przez średnią wartość obliczoną z tej liczby i kilku z nią sąsiadujących. Przy obliczeniu średniej można przy tym różnie ważyć poszczególne liczby, na przykład tak, by skrajne mniej wpływały na średnią niż centralne liczby z grupy uśrednianej. Splotem jest takie samo wygładzenie, lecz uogólnione na wypadek funkcji ciągłych (a nie ciągów liczbowych). Obie funkcje splatane mogą być w zasadzie dowolne i jedna z nich gra rolę ciągu liczbowego, a druga może być rozumiana jako funkcja ważąca, jednakże tego typu rozróżnienie jest zbyteczne, gdyż wynik operacji nie zależy od przypisania ról. Dotychczasowe operacje sumowania, występujące przy uśrednianiu, w splocie zastępowane są przez odpowiednie całki. Jedno z najbardziej wszechstronnych narzędzi w analizie częstościowej układów (elektrycznych, mechanicznych) i sygnałów wynika z własności splotu ujmowanej w następujące twierdzenie: widmo funkcji splecionych jest iloczynem widm funkcji splatanych. Filtrowanie polega na ograniczaniu widm do wybranych okien i można to zrobić przez pomnożenie widma sygnału przez funkcję okna bądź przez splot samego sygnału z transformatą Fouriera wymaganej funkcji okna. Zazwyczaj dąży się do prostokątnych funkcji okna, aby nie zniekształcać widma mocy sygnału w przepuszczanym zakresie częstości. Transformatami Fouriera takich okien są funkcje typu (sin x)/x (rys. C i F). Funkcja przedstawiona na rys. G jest splotem dwóch identycznych funkcji prostokątnych z rys. F, dlatego jej widmo jest kwadratem widma funkcji prostokątnej przedstawionego z prawej strony rys. F.
DELTA DIRACA
Jeżeli liczbę punktów używanych do obliczenia średniej przy wygładzaniu (omówionym przy określaniu splotu) ograniczymy do jednego (inaczej mówiąc, położymy zero na wszystkie wagi z wyjątkiem jednej), wygładzanie sprowadzi się do odtworzenia oryginalnego ciągu. Dla przypadku ciągłego, tzn. dla splotu, rolę takiej szczególnej funkcji ważącej spałnia delta Diraca, która jest wszędzie zerem z wyjątkiem jednego punktu, w którym ma wartość nieskończoną. Powierzchnia zawarta między przebiegiem delty a osią odciętych jest przy tym jednością, dlatego nazywa się ją też impulsem jednostkowym. Wynikiem scałkowania dowolnej funkcji pomnożonej uprzednio przez deltę jest wartość owej funkcji w miejscu ustawienia delty. Jak widać nie jest to zwykła funkcja; tworami tego typu zajmuje się teoria dystrybucji. Z twierdzenia o splocie, o którym pisaliśmy wcześniej, wynika nieuchronnie, że widmo delty Diraca jest równomierne i nieograniczone (rys. A). W praktyce nigdy nie mamy do czynienia z deltą Diraca w czystej formie, lecz krótkie (w czasie lub przestrzeni) impulsy dobrze odzwierciedlają własności tego osobliwego tworu, co skrzętnie wykorzystuje się w wielu dziedzinach nauki i techniki (np. fizyka, tomografia czy radiotechnika). Istnieje wiele różnych reprezentacji delty Diraca, ale chyba najprostszą jest ta, która określa ją jako granicę ciągu funkcji prostokątnych o jednostkowych powierzchniach (zawartych między tą funkcją i osią odciętych) i malejących do zera szerokościch. Równoważną reprezentację delty dostaniemy, transformując powyższy ciąg funkcji prostokątnych do dziedziny częstości i biorąc granicę z przeciwnej strony — przy szerokościach zmierzających do nieskończoności. Oczywiście, jest to teraz granica funkcji typu (sin x)/x. Ilustrują to rysunki A, C, F i H w takiej lub odwrotnej kolejności w zależnosci od wyboru dziedziny. (kb)
|
Centralny składnik charakterystyki kierunkowej, zwany wiązką główną, ma szerokość 2λ/D. W przypadku trójwymiarowej paraboloidy obrotowej charakterystyka kierunkowa wygląda podobnie, lecz jej listki boczne, tzn. wtórne ekstrema, są znacząco mniejsze.
Można pokazać, że transformata Fouriera prostokątnego okna naszego dwuwymiarowego filtru częstości przestrzennych jest identyczna z otrzymaną przed chwilą funkcją opisującą charakterystykę kierunkową teleskopu. Okazuje się, że dla dowolnego układu anten, teraz już także trójwymiarowego, wypadkowa charakterystyka kierunkowa i jego widmo częstości przestrzennych są parą transformat Fouriera. Wypowiemy jeszcze jedno równie ogólne i równie pożyteczne stwierdzenie wynikające z tego, że system antenowy jest filtrem dla widma przestrzennego kątowego rozkładu jasności źródła: odpowiedź systemu antenowego jest splotem rozkładu jasności z charakterystyką kierunkową systemu. Widać to wyraźnie w przypadku źródła punktowego, któremu przypisuje się własności specjalnego rodzaju funkcji impulsowej, nazywanej deltą Diraca. W tej sytuacji, jak już wiemy, na wyjściu systemu pojawi się sama charakterystyka kierunkowa instrumentu (splot delty Diraca z dowolną funkcją odtwarza tę funkcję).
Odwracając niejako sytuację, zauważamy że system antenowy o nieskończenie wielkiej aperturze miałby nieskończenie wąską wiązkę główną bez listków bocznych, czyli charakterystykę kierunkową typu delty Diraca. Taki system odtwarzałby z kolei bez zniekształceń wprost rozkład jasności źródła.
Splotowi funkcji w dziedzinie przestrzeni odpowiada mnożenie ich widm w dziedzinie częstości. Analizując powyższe przypadki na widmach, trzeba pamiętać, że widmo delty Diraca jest równomierne w całym zakresie, co powoduje, że np. sygnał impulsowy (delta) po przejściu przez jednobarwny filtr przepuszczający tylko bardzo wąskie pasmo staje się czystą sinusoidą o amplitudzie niezależnej od częstości (bądź częstotliwości), na którą nastrojono filtr.
W tym miejscu możemy już rozpoznać istotną różnicę pomiędzy teleskopem optycznym i radiowym. Teleskopy optyczne mają tak wielkie apertury (licząc w długościach fali), że ich charakterystyka kierunkowa jest bliska delcie Diraca (bardzo szerokie widmo przestrzenne) i dlatego zwykła suma promieni skupionych w pobliżu ogniska lustra parabolicznego daje od razu przyzwoite obrazy gwiazd i innych obiektów. W kontekście przeprowadzonej już dyskusji możemy także powiedzieć, że obraz ten jest wynikiem prostego zsumowania wszystkich listków interferencyjnych, pojawiających się na wyjściach wszystkich elementarnych interferometrów, na jakie możemy rozłożyć w myślach paraboliczny teleskop optyczny.
 |
|
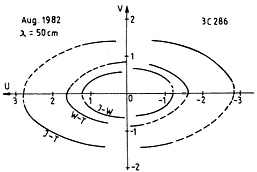
Rys. 2. Przykładowe wypełnianie płaszczyzny częstości przestrzennych dla: kwazara 3C286, dla przypadku trzech teleskopów biorących udział w sesji obserwacyjnej VLBI w sierpniu 1982 r. Poszczególne fragmenty elips dotyczą baz utworzonych przez stacje Jodrell Bank (J, Wielka Brytania), Toruń (T) i Westerbork (W, Holandia). Jednostką skali częstości przestrzennych jest 106λ. |
Odtworzenie obrazu radioźródła z jego widma (w postaci amplitud i faz listków interferencyjnych) ideowo jest sprawą prostą. Jak wiemy, należy tylko przekształcić zmierzone widmo wg Fouriera. Niestety, praktyka nie jest aż tak prosta. Po pierwsze, pomiary obarczone są błędami powstającymi zarówno wskutek niedoskonałości instrumentu pomiarowego, jak i w wyniku naturalnych fluktuacji fazy i drogi rozchodzenia się sygnałów przez turbulentne i różne ośrodki (atmosfera Ziemi i przestrzeń kosmiczna). Po drugie, rzeczywistość jest trójwymiarowa, w związku z czym np. supersynteza, którą tak doskonale wypełniało się aperturę w dwóch wymiarach, teraz okazuje się znacznie mniej efektywna. Przede wszystkim mamy teraz do czynienia nie z osią częstości przestrzennych, lecz z całą płaszczyzną nazywaną w literaturze płaszczyzną uv. Jest ona prostopadła do kierunku obserwowanego źródła, a prosty interferometr reprezentuje na niej pojedynczy punkt wyznaczony przez rzut wektora bazy na wzajemnie prostopadłe osie u i v. Wskutek obrotu Ziemi koniec bazy widziany z kierunku źródła zatacza w ogólności elipsę (koło, jeśli źródło znajduje się na biegunie nieba, a odcinek prostej, gdy na równiku), a zatem repertuar dostępnych częstości przestrzennych jest ograniczony do takiej właśnie krzywej. Wynika z tego, że obserwacja prowadzona nawet przez znaczny ułamek doby nijak nie zapełni apertury, czy też płaszczyzny uv (rys. 2). Dopiero wiele różnie zorientowanych interferometrów daje szansę na jako tako równomiernie próbkowany, dwuwymiarowy filtr częstości przestrzennych i odpowiadającą mu charakterystykę kierunkową o względnie niskim poziomie listków bocznych.
 |
|
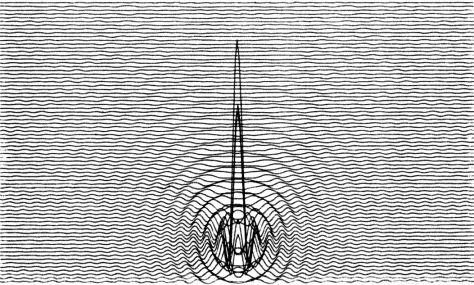
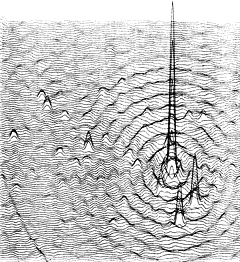
Rys. 3. Fragment zsyntezowanej charakterystyki kierunkowej, złożonej z 67 baz 1-milowego teleskopu trójantenowego w Cambridge (Wielka Brytania), pracującego na częstotliwości 408 MHz. Ponieważ jednorazowo system ten pozwala zsyntezować zaledwie trzy bazy, to na złożenie takiej charakterystyki przeznacza się wiele dni obserwacji |
Na rys. 3 pokazano przykład zsyntezowanej charakterystyki kierunkowej, na którą złożono 67 interferometrów utworzonych z trójantenowego systemu z Cambridge (Wielka Brytania). Ponieważ system ten pozwala na jednoczesną pracę jedynie trzech interferometrów, to na syntezę prezentowanej charakterystyki zużywa się wiele dni obserwacji tego samego obszaru nieba — codziennie z innym ustawieniem anten (jedna antena tego systemu jest ruchoma).
Ze względu na złożoność i czasochłonność tej techniki w obserwacjach VLBI udział bierze zwykle tylko kilka stacji a teleskopy są nieruchome. Z n teleskopów można utworzyć
| ( | n 2 |
) = |
n(n – 1)
|
Działanie CLEAN-u polega na wyszukaniu na brudnej mapie miejsca o największej jasności (natężeniu), odjęciu od całej mapy zsyntezowanej charakterystyki kierunkowej skierowanej swym maksimum wzmocnienia na znalezione miejsce i znormalizowanej do pewnego ułamka (np. 50%) natężenia w tym miejscu. Proces takiego odejmowania powtarza się wielokrotnie, aż do pozbycia się wszystkich znaczących „źródeł" obecnych na brudnej mapie. Czystą mapę uzyskuje się, wkładając z powrotem w znalezione miejsca mapy charakterystyki kierunkowe proporcjonalne do oryginalnych natężeń, ale już „czyste", pozbawione listków bocznych.
 |
|
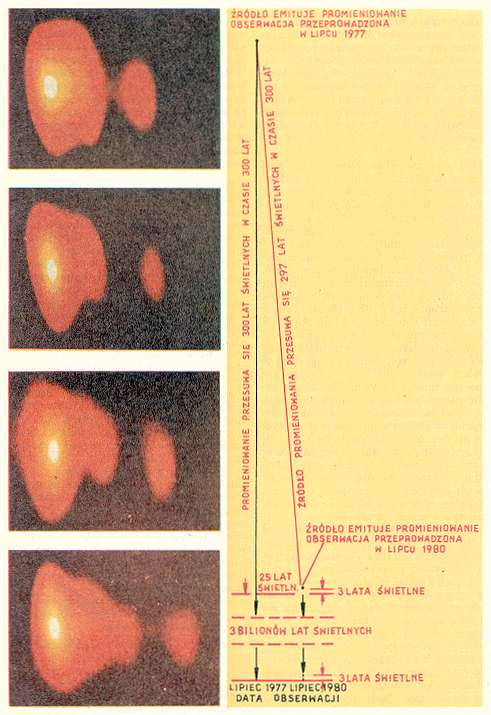
Fot. 4. Seria zsyntezowanych radiowych obrazów „nadświetlnego" kwazara 3C273 wykonanych z rozdzielczością 0,001" w latach 1977–1980. Do obserwacji używano 3 lub 4 teleskopy w USA oraz 100 m teleskop w Effelsbergu (RFN). W ciągu 3 lat obiekt wyrzucony ze źródła przesunął się o 25 lat świetlnych |
 |
|
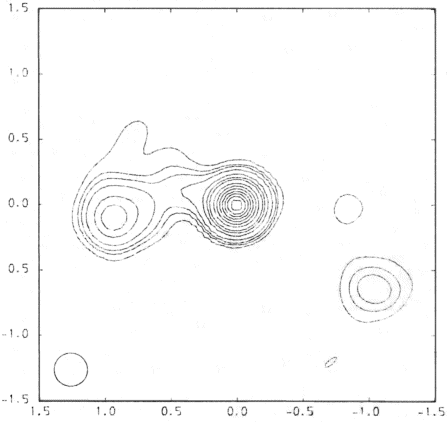
Rys. 4. Końcowy wynik obserwacji kwazara 3C309.1 4-teleskopowym interferometrem z Jodrell Bank. Przy opracowywaniu tej mapy korzystano z metody zamkniętej fazy i zamkniętej amplitudy. Wykres przedstawia źródło w postaci mapy konturowej. Rysunek obejmuje obszar 3"×3" w kierunku deklinacji (w górę) i rektascensji. Strumień tego źródła w maksimum wynosi 4·10–26 Wm–2Hz–1 |
Z teorii analizy widmowej wiadomo, że na to, by móc jednoznacznie odtworzyć obraz z jego widma z zadaną rozdzielczością kątową, trzeba dysponować kompletnym widmem próbkowanym równomiernie i dostatecznie gęsto na całej płaszczyźnie uv, aż do zadanej częstości granicznej. Radioastronomom używającym techniki VLBI dokuczają nie tylko braki w pokryciu płaszczyzny uv, ale często do błędów pomiaru amplitudy dochodzi kompletny brak fazy widma (listków interferencyjnych), gdyż z powodu dużych błędów w jej pomiarach staje się po prostu zupełnie nieprzydatna do analizy (by nie zostawić wrażenia, iż źródłem tych błędów jest niedbalstwo obserwatorów, dodajmy, że
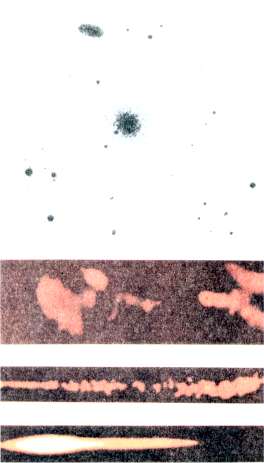 |
| Fot. 5., Wyrzuty w eliptycznej galaktyce NGC6251. Górne zdjęcie wykonano przy zastosowaniu palomarskiego teleskopu 5-metrowego, a pozostałe są zsyntezowanymi mapami radiowymi o coraz większych rozdzielczościach kątowych. Dolna mapa została wykonana technikami VLBI, a widoczny na niej krótki wyrzut ma szerokość zaledwie około 0,0001" |
Niech za przykład posłuży metoda bezfazowego odtwarzania map hybrydowych opracowana przez J. Baldwina i P. Warnera w 1976 r. Korzysta się w niej z mapy próbnej (próbnego modelu rozkładu jasności źródła) zawierającej jedynie niektóre z prawdziwych składników. Taką mapę i można uzyskać na podstawie pomiarów samych amplitud listków interferencyjnych. Mapę próbną transformuje się „fourierowsko" do dziedziny częstości w celu otrzymania funkcji widzialności, czyli widma przestrzennego modelowego źródła. Z tego widma bierze się teraz jedynie fazy i dołącza je do obserwowanych amplitud. Tak skomponowane widmo zawierające obserwowane amplitudy i modelowe fazy może być użyte do wykonania nowej, poprawionej mapy próbnej, zwanej hybrydową. Po 2 – 3 cyklach poprawiania map próbnych dostaje się mapę o jakości mapy prawdziwej, mimo że obserwowane widmo było zupełnie pozbawione fazy. Przyjęło się później terminem „hybrydowe" określać ogólniejszą klasę map zrekonstruowanych z niepełnych danych obserwacyjnych i wykonanych niekonwencjonalnymi metodami.
Jest dość oczywiste, że błędy instrumentalne i powstałe na drodze rozchodzenia się sygnałów powinny prowadzić do pogorszenia rozdzielczości wyników pomiarów. Do celów VLBI, gdzie ten problem ma pierwszorzędną wagę, opracowano specjalne metody obróbki sygnałów, które eliminują (sic!) wszystkie błędy fazy i amplitudy listków interferencyjnych powstałe gdziekolwiek na drodze od źródła do miejsca odbioru, a nawet w systemach odbiorczych. Są to metody oparte na wtórnych wielkościach powstałych z kombinacji zmierzonych (z błędami) faz lub amplitud. To, co pozostaje w takich kombinacjach, nazywanych zamkniętymi fazami lub zamkniętymi amplitudami, jest związane li tylko ze strukturą źródła.
 |
|
Rys. 5. Wynik obserwacji pozagalaktycznego źródła 5C7 111 (w środku mapy) zrealizowanej za pomocą teleskopu 1-milowego z Cambridge w 1974 r. w ramach sporządząnia przeglądu 5C7 na częstotliwości 1407 MHz. Przy syntezie tego obrazu wykorzystano 42 konfiguracje elememarnych interferometrów zrealizowanych w czasie 2 miesięcy obserwacji. Okręgi wokół silniejszych źródeł pochodzą od listków bocznych zsyntezowanej charakterystyki kierunkowej |
By choć trochę przybliżyć ideę tych metod wyobraźmy sobie trójantenową sieć VLBI, która tworzy trzy interferometry proste. Jak już mogliśmy się przekonać, w przypadku obserwacji źródła punktowego faza listków interferencyjnych jest różnicą faz sygnałów odebranych w poszczególnych stacjach. Zatem w naszym systemie trójantenowym fazy listków na dwóch bazach różnią się między sobą o fazę listków na trzeciej bazie — i to niezależnie od wszelkich zakłóceń, którym uległy sygnały zapisane w każdej ze stacji z osobna. Prosta suma trzech faz w zamkniętym trójkącie baz powinna więc znikać, a jeśli nie znika to ta pozostałość świadczy o niepunktowości obserwowanego źródła i niesie informację o jego strukturze. Podobny efekt znoszenia się błędów można uzyskać dla amplitud listków interferencyjnych, ale trzeba wówczas dysponować przynajmniej czterema teleskopami i kombinacje nie są już sumami, lecz iloczynami. Procedury rekonstrukcji map wykorzystujące te zamknięte wielkości nazywa się autokalibracyjnymi. Mapę przedstawioną na rys. 4 wykonano w oparciu o takie właśnie algorytmy.
Dzięki doskonaleniu metod opracowywania wyników obserwacji VLBI, naziemny interferometr osiąga obecnie zdolność rozdzielczą ograniczoną jedynie rozmiarami bazy. Oznacza to, że dotychczasowe osiągnięcia mogą być jeszcze poprawione prawie dziesięciokrotnie po przejściu do zakresu najkrótszych fal radiowych. Realna wydaje się być rozdzielczość niewiele gorsza niż 0,00001". Dalsza poprawa będzie możliwa dopiero po wyniesieniu stacji VLBI w kosmos. Przewiduje się, że w pierwszym etapie w przestrzeni pozaziemskiej znajdzie się jedna stacja jako rozszerzenie istniejących sieci stacji naziemnych. Istnieją także projekty optycznych VLBI. Tak np. w projekcie TRIO przewidziano kosmiczny interferometr, składający się z trzech teleskopów optycznych, którego rozdzielczość kątowa ma sięgać 0,00001". Jak wskazuje dotychczasowe doświadczenie, wysiłek włożony w poprawę rozdzielczości instrumentów astronomicznych zostaje zawsze sowicie wynagrodzony wynikami obserwacji.