POSTĘPY ASTRONOMII
Tom XXIX (1981). Zeszyt 1
ANALIZA BŁĘDÓW SYSTEMATYCZNYCH
W TORUŃSKICH POMIARACH STRUMIENIA
RADIOWEGO PROMIENIOWANIA SŁOŃCA
Cześć I
CZYNNIKI NATURALNE
K A Z I M I E R Z M. B O R K O W S K I
Katedra Radioastronomii
Uniwersytetu M. Kopernika (Toruń)
(Otrzymano 11 marca 1980
r.)
|
S t r e s z c z e n i e — Artykuł
poświęcony jest dyskusji kilkunastu czynników wpływających na pomiary
radiowego promieniowania Słońca na dłuższych falach ze szczególnym
wyróżnieniem toruńskich obserwacji na częstości 127 MHz. W tej części
rozważa się wzorce gęstości strumienia, eliptyczność orbity Ziemi i
tłumienie atmosfery ziemskiej.

AN ANALYSIS OF SYSTEMATIC
ERRORS OF THE TORUN SOLAR RADIO FLUX MEASUREMENTS. Part I. NATURAL
FACTORS. A b s t r a c t — The article is devoted to a
discussion of various factors influencing solar radio flux
measurements at longer waves, with special stress on
Toruń observations at 127 MHz. In this part standards of the flux
density, ellipticity of the Earth orbit and terrestrial atmosphere
attenuation are considered. |
1. WSTĘP
Podstawowym problemem
obserwacji Słońca na falach metrowych są rozbieżności w wyznaczeniach
bezwzględnego strumienia promieniowania Słońca. Istniejące
rozbieżności można często sprowadzić do różnicy w jednostkach
przyjmowanych dla gęstości strumienia będącej wynikiem błędów
systematycznych popełnianych przy obliczeniach. Mimo to każde
obserwatorium nazywa swoją jednostkę jednostką słoneczną, mając na
uwadze jej ścisłą wartość: 1 su = 10-22
W·m-2·Hz-1.
Toruńskie
wyniki obserwacji Słońca na częstości 127 MHz nie wyróżniają się
niczym szczególnym w tym względzie. W tej pracy podejmę próbę
nawiązania toruńskiej jednostki strumienia do tej ze skali
bezwzględnej. Z analizy kilkunastu czynników systematycznie
wpływających na wyniki pomiaru strumienia wynika, że pomimo, iż są
one W większości przypadków zaniedbywalnie małe W porównaniu z
dokładnością pomiarów, to jednak wypadkowy efekt jest zaskakująco
duży. Spowodowane jest to z jednej strony tym, że istnieją pojedyncze
czynniki mające przemożny wpływ na wyniki (dudnienia i skale
strumienia), a z drugiej – że większość z małych przyczynków
jest jednokierunkowa (w kierunku zaniżania wyników końcowych –
sumarycznie o ok. 8%).
Dyskusję przeprowadzę z uwzględnieniem
wszystkich toruńskich obserwacji interferometrycznych (od 1960 r.),
jednakże z większym naciskiem na obserwacje z okresu po 1972 r.,
kiedy wprowadzono do służby nowy instrument. Ten nacisk wynika z
faktu, że w tym drugim okresie zajmowałem się obserwacjami
bezpośrednio. Ponadto parametry ostatniego instrumentu są znane z
większą dokładnością, a pewne pomiary można było wykonać bezpośrednio
z istniejącym jeszcze systemem odbiorczym.
Chociaż cała praca
ogranicza się do wyznaczenia poprawek do pomiarów właściwych ściśle
określonemu instrumentowi i częstości, to wszystkie z omawianych
czynników przedstawię tak, aby można było wykorzystać podane fakty w
przypadkach innych instrumentów i innych zakresów częstości.
Szczególnie dotyczy to niniejszej części pracy, w której omówię
aktualne wzorce strumienia, poprawki związane z ruchem Ziemi wokół
Słońca i wpływ atmosfery ziemskiej na obserwowany strumień
promieniowania Słońca. W części II zostaną przedstawione czynniki
związane z metodyką obserwacji i opracowania danych –
właściwymi toruńskiej służbie Słońca.
2. WZORCE STRUMIENIA
Doświadczenie wskazuje, że
istotnym źródłem rozbieżności wyników uzyskiwanych w
różnych
obserwatoriach są założenia o bezwzględnym strumieniu
radioźródeł kalibracyjnych (B o r k o w s k i i in. 1980, B o r k o
w s k i 1980). Trudność polega na tym, że istnieje wiele opracowań
skal strumienia (np. B o r k o w s k i 1975) i ciągle pojawiają się
nowe, oparte na bogatszym materiale obserwacyjnym. Częste zmiany skal
stosowanych W danym obserwatorium wprowadzałyby zbędny chaos w
postaci braku ciągłości publikowanych na bieżąco wyników. Z tego
powodu, nawet gdy odstępstwa skal są znaczące, wiele obserwatoriów
świadomie utrzymuje stare nawiązania w celu zachowania wewnętrznej
zgodności wyników. Odstępstwa skal wyraża się określonym
współczynnikiem korygującym, podawanym okresowo do wiadomości
odbiorców. Niestety, praktyka taka jest stosowana li tylko na
częstościach większych od 500 MHz (np. QBSA 1977), dla których –
dzięki pracom specjalnie utworzonej grupy roboczej przy URSI –
wprowadzono jednolite metody sprowadzania wyników obserwacji Słońca
do wspólnej skali strumienia.
Szczęśliwie się składa, że
toruńskie obserwacje Słońca były w przeszłości kalibrowane głównie za
pomocą radioźródła Cassiopeia A (Cas A) i jest znana wartość
strumienia tego źródła, przyjmowana przez wiele lat za niezmienną
(1,5 su, zgodnie z pracą W h i t f i e l d a 1959). Od roku 1972
wprowadzono kilka zmian w przyjęciach strumieni podstawowych źródeł
kalibracyjnych (B o r k o w s k i 1977), jednakże większość z tych
obserwacji z innych powodów (B o r k o w s k i 1977) powinna być
zredukowana na nowo, wobec czego owe zmiany nie są tak
istotne.
Ostatnio stosowana skala strumienia była oparta na
pracach B a a r s a i H a r t s u i j k e r a (l972) i D e n t a
i in. (1974). Została ona niedawno udoskonalona przez B a a r s a
i in. (1977) i wydaje się, że jest to obecnie najbardziej wiarogodne
wyznaczenie. Według tej najnowszej skali gęstość strumienia Cas A
S(ƒ) (w jednostkach su) na początku 1965 r. w
zakresie częstości od 22 do 300 MHz opisuje zależność:
|
lg S(f) = 1,625 – 0,634·lg
f – 0,023(lg f)2,
| (1) |
gdzie częstość f jest wyrażona w MHz. Na wyższych
częstościach (do 31 000 MHz) obowiązuje związek lg S(f)
= 1,880 – 0,792·lg
f. Strumień promieniowania Cas A wykazuje wiekowy spadek
zależny od częstości, który wyrażony w procentach na rok wynosi:
(B a a r s i in. 1977). Wzory (1) i
(2) dla określonej częstości wygodniej jest przedstawić w postaci
jednej funkcji czasu. W przypadku częstości 127 MHz jest to
funkcja:
|
S = 1,5466·(0,9876)t
– 1965, | (3) |
gdzie t jest epoką wyrażoną
w latach. Na przykład, w latach 1959,0 i 1980,0 gęstość strumienia
Cas A na częstości 127 MHz wynosiła odpowiednio 1,67 i 1,28
su.
Drugie podstawowe źródło kalibracyjne na północnej półkuli
nieba – Cyg A – można uważać za
niezmienne w czasie. Według wyżej
przedstawionej skali, w zakresie częstości od 20 do 2000 MHz, gęstość
strumienia tego źródła opisuje zależność:
|
lg S(ƒ)
= 0,695 + 0,085·lg
f – 0,178·(lg
f)2, | (4) |
gdzie: częstość f wyrażona
jest w MHz, a strumień S – w jednostkach słonecznych (su).
Gęstość strumienia Cygnusa A na częstości 127 MHz wynosi 1,22 su.
B
a a r s i in. (1977) oceniają dokładność swojej skali w przypadku
Cas A na ok. 2% (wzór (1) w zakresie częstości > 100 MHz), a w
przypadku Cyg A – 5% (wzór (4)). Trzeba jednak pamiętać, że
przy obliczaniu strumienia Cas A, zwłaszcza dla epok znacznie
odległych od 1965 r., wprowadza się dodatkowy błąd, będący wynikiem
niepewności współczynnika (2).
Łatwo jest sprawdzić, że na to,
by sprowadzić toruńskie wyniki obserwacji Słońca z 1959 r. do obecnie
stosowanej skali strumienia trzeba je wymnożyć przez czynnik ok. 1,11
(zwiększyć o 11%). Wspomnieć warto, że w czerwcu 1979 r. w Nançay
odbyło się spotkanie robocze reprezentantów kilku europejskich
obserwatoriów słonecznych, na którym m.in. uzgodniono jednolitą skalę
kalibracyjną do wyznaczeń strumienia promieniowania Słońca. Skala ta
niewiele odbiega od propozycji B a a r s a i in. (1977). Strumień
Cyg A opisuje w niej zależność (4), zaś strumień Cas A wyrażono
wzorem:
|
S(f,t) = So ea(t
– to)
f αo+
b(t – to), |
gdzie:
to = 1980,0 rok, a = –0,0097 rok–1,
b = 0,00126 rok–1 i dla częstości 0,2 < f
< 30 GHz αo
= –0,770 i So = 0,2720 su, zaś dla częstości
0,02 < f < 0,2 GHz αo
= –0,681 i So = 0,3140 su (E l g a r ö y i
in. 1980).
3. ELIPTYCZNOŚĆ ORBITY
ZIEMI
Ponieważ odległość Ziemi od
Słońca zmienia się W ciągu roku, to również gęstość
strumienia
promieniowania Słońca obserwowana na Ziemi ulega
modulacji. Wyniki radiowych obserwacji Słońca koryguje się więc przez
pomnożenie zmierzonych wartości strumienia przez kwadrat aktualnej
odległości (wyrażonej w jednostkach astronomicznych) Ziemia –
Słońce. Czynnik ten zmienia się w granicach od 0,966 do 1,034 (tj. ±
3,4%), przy tym jest większy od jedności w okresie od kwietnia do
września (rys. 1).
Ze względu na zakłócające odbicia
promieniowania od gruntu przed antenami (o tym czynniku będzie
jeszcze mowa w części II tej pracy), toruńskie wyznaczenia strumienia
są wiarogodne tylko w okresie, gdy Słońce przebywa stosunkowo wysoko
nad horyzontem (w praktyce od maja do sierpnia). W tym okresie Ziemia
znajduje się najdalej od Słońca, co oznacza,że pomiary są
systematycznie zaniżane. Zaniżanie to wynosi średnio ok. 2%
strumienia.
Rzeczywistą odległości Ziemi od Słońca w ciągu
roku podają prawie wszystkie roczniki astronomiczne. W praktyce
obserwacyjnej wszakże wygodniej jest mieć możliwość szybkiego
obliczenia tej wartości.
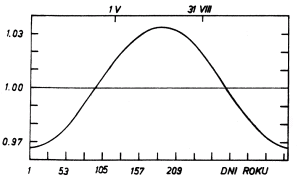
Rys. 1. Przebieg
współczynnika korygującego pomiary strumienia promieniowania
Słońca
na efekt wynikający z eliptyczności orbity Ziemi w roku 1978
Pozwala na to wzór, który znalazłem
u G r a f a (1974) i który można napisać w formie współczynnika
korekcyjnego:
|
R2 = [1 – e cos(T
+ e sin T)]2, | (5) |
gdzie: R
jest odległością Ziemia – Słońce, e –
ekscentrycznością orbity Ziemi (w latach 80. e ≈
0,01672), T = (d – 3,05 + Frac[(r –
1)/4]) 2π/365,25 (Frac
oznacza tutaj część ułamkową), d jest numerem porządkowym dnia
w roku (1 stycznia d = 1), a r – rokiem (np.
1980). Współczynnik obliczony według powyższego algorytmu może różnić
się od rzeczywistego co najwyżej o 2·10–4,
co całkowicie satysfakcjonuje wymagania obserwatorów Słońca.
4. TŁUMIENIE
ATMOSFERYCZNE
Ze względu na własności elektryczne
atmosferę Ziemi dzieli się na dwie warstwy: atmosferę neutralna (z
troposferą i stratosferą) i jonosferę (z warstwami D, E, F1
i F2). Granice pomiędzy poszczególnymi warstwami zmieniają
się w wysokości, albo nawet znikają, w zależności od pory dnia, pory
roku, położenia geograficznego, aktywności Słońca i innych
czynników.
Fale elektromagnetyczne rozchodzące się w
neutralnej atmosferze ulegają w ogólności pochłanianiu, zmianom fazy
i kierunku propagacji. Z wyjątkiem tego ostatniego, zjawiska te są
zaniedbywalne na falach metrowych (do ok. 500 MHz), stanowią
natomiast ważne ograniczenie na mikrofalach (np. W a t e r s 1976; C
r a n e 1976; H a g f o r s 1976). Absorpcja fal w dolnych warstwach
atmosfery wynika z obecności wolnych cząstek i zawiesin pyłów oraz
kropel wody w postaci mgły i deszczu. Teoretyczne obliczenia
tłumienia wynikającego z obecności tlenu w atmosferze i przy deszczu
o nasileniu 30 mm/h prowadzą do wartości od 0,8 do 0,05 dB na
częstościach od 3 do 0,3 GHz, odpowiednio (M i l l m a n 1965).
O
ile dolne warstwy atmosfery charakteryzuje równomierny i stały skład
chemiczny, to powyżej 80 – 90 km nad powierzchnią Ziemi zaczyna
się rozwarstwianie gazów (cięższe gazy gromadzą się niżej). W
rozrzedzonej atmosferze zachodzi dysocjacja cząsteczek tlenu (od
wysokości 90 km) i azotu (powyżej 220 km) i ich jonizacja. Istnienie
warstw zjonizowanych spowodowane jest prawie całkowicie przez
promieniowanie Słońca (promieniowanie nadfioletowe, miękkie X i
kosmiczne) i w pewnym stopniu meteory. W związku z tym stan jonosfery
jest ściśle skorelowany z przebiegiem 11-letniego cyklu aktywności
Słońca, a zmiany warstw D i E z porami roku są dość regularne i
związane z odległością zenitalną Słońca (F o k k e r, R o o s e n
1963). Dobitnie manifestuje tutaj swoją obecność cykl dobowy (np. R a
t c l i f f e 1972).
Ponieważ stopień nasilenia większości
zjawisk towarzyszących rozchodzącej się fali radiowej w
jonosferze
jest odwrotnie proporcjonalny do kwadratu częstości, to dla wyższych
częstości są one na ogół zaniedbywalne.
Mechanizm tłumienia
sygnałów elektromagnetycznych w jonosferze polega na przekazywaniu
energii promienistej wolnym elektronom (wprawianym w ruch wibracyjny
z częstością sygnału), które w wyniku zderzeń z innymi cząstkami
atmosfery przekształcają ją na energię ruchu (podgrzewanie ośrodka).
W ogólności, w ośrodku jednorodnym, rozpraszającym i częściowo
przewodzącym tłumienie fal elektromagnetycznych opisuje znany
eksponencjalny spadek amplitudy: E = Eoexp(–ks),
gdzie s jest drogą, k – współczynnikiem
załamania, a E i Eo – natężeniami pola
elektrycznego fali przed i po jej przejściu przez warstwę tłumiącą.
Całkowite tłumienie wyrażone w decybelach wynosi:
|
20 lg exp(– |
s2
∫
s1 |
k ds) = –8,686 | s2
∫
s1 | k
ds. | (6) |
W celu uproszczenia analizy, zwykle
rozpatruje się osobno rozchodzenie się sygnału w przypadku, gdy
współczynnik załamania ośrodka jest znacząco mniejszy od jedności
(propagacja dewiacyjna) i gdy ten współczynnik jest bliski jedności
(propagacja niedewiacyjna). Na częstościach większych niż 100 MHz w
jonosferze dominuje propagacja niedewiacyjna i wtedy spełniony jest
warunek fc2 << f2,
gdzie fc jest częstością krytyczną (fale o niższych
częstościach są odbijane od jonosfery), a f – częstością
sygnału. Można pokazać (R a w e r 1976), że wtedy dla f > 5
MHz i gdy (f ± |fl|) >> (v/2π)2
(ten warunek jest w praktyce zawsze spełniony na falach metrowych)
także zachodzi:
|
k = 1,344·10–16
vN(f ± |fl|) –2,
| (7) |
gdzie: fl jest częstością
żyromagnetyczna odpowiadającą składowej pola magnetycznego o kierunku
rozchodzenia się fali (w MHz), v – częstością zderzeń
(Hz), N – gęstością elektronów (m–3), a
k ma wymiar km–1. Złożenie wzorów (6) i (7)
prowadzi do całkowitego tłumienia:
| A = 1,67·10–15∫ | s2
s1 |
vN(f ± |fl|)
–2 ds. |
| (8) |
Jeśli można zaniedbać pole
magnetyczne Ziemi (częstość żyromagnetyczna w warstwie F jonosfery
nad obszarem Polski wynosi ok. 1,3 MHz), to mianownik wyrażenia
podcałkowego w (8) można wynieść przed znak całki. W takim przypadku
i dla częstości 127 MHz wzór (8) upraszcza się do:
| A = 7,24·10–20∫ | s2
s1 |
vN ds. |
| (9) |
Znajomość rozkładów gęstości
elektronów i częstości zderzeń w atmosferze pozwoliłaby na
łatwe
obliczenie tłumienia sygnałów za pomocą wzoru (9). Wykonałem
kilka prób całkowania korzystając z dostępnych rozkładów, jednakże
wyniki wskazywały tłumienie znacznie mniejsze niż się obserwuje.
Można to złożyć na karb uproszczenia modelu i niezbyt dobrej
znajomości rozkładu częstości zderzeń. W rzeczywistości rozkład ten,
jak też rozkład gęstości elektronów, zmienia się tak często i zależy
od tak wielu czynników, że trudno przewidzieć jego parametry nawet z
wyprzedzeniem kilku godzin. Na podstawie przeglądu literatury wydaje
się dość bezpieczne przyjęcie, że tłumienie jonosfery w porze nocnej
jest ok. 10 razy mniejsze niż w południe. Wobec małości tłumienia
dziennego fakt ten upoważnia do zaniedbania tłumienia nocnego na
częstościach rzędu 100 MHz i większych.
Dla oceny tłumienia
dziennego zebrałem dostępne w literaturze wyniki i przeliczyłem je na
częstość 127 MHz zgodnie z zależnością typu 1/f2,
która w praktyce jest dosyć dobrze spełniona na częstościach
większych od ok. 10 MHz. Zestawienie tych wyników zawiera tab. 1. Z
braku miejsca nie będę dyskutował wszystkich rezultatów, ograniczając
się do kilku uwag.
T a b e l a 1
Dzienna
absorpcja atmosferyczna w zenicie
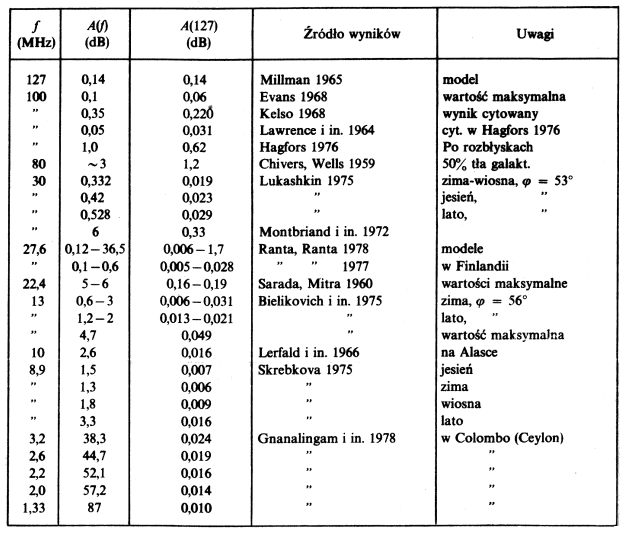
Wszystkie
wyniki dotyczą obliczeń lub pomiarów tłumienia jednokierunkowego w
zenicie. Wynik Mi l l m a n a (1965) odczytałem z przytoczonego tam
wykresu opartego na modelu teoretycznym. Model ten wydaje się
opierać na zawyżonym rozkładzie gęstości elektronów. M i l l m a n
przyjął na integralną gęstość elektronów wartość 5·1017
m–3, gdy tymczasem należałoby przyjąć wartość około
dwukrotnie mniejszą (np. E s s e x 1978; T a y l o r 1966 czy S c h u
n k i N a g y 1978).
S k r e b k o v a (1975) zbudowała cały
szereg szczegółowych modeli uzyskując znakomitą zgodność z
obserwacjami tłumienia (w tab. 1 są wartości obserwowane), ale jej
modele rozkładu gęstości elektronów wydają się być zaniżone. W
maksimum warstwy F znajduję tam gęstości mniejsze od 5·1011
m–3, gdy w większości dostępnej literatury parametr
ten osiąga lub przekracza poziom 1012 m–3
(np. F r i h a g e n 1966; H a g f o r s 1976; B e y n o n i W i l
l i a m s 1978 czy K ö h n l e i n 1978).
Z przytoczonych
wyników na częstości 127 MHz wydają się realne skrajne tłumienia
rzędu 0,5 dB lub więcej z jednej strony i 0,005 dB – z drugiej.
Dla okresu letniego na średnie (wciąż jednak dość dowolne) tłumienie
można przyjąć wartość 0,03 dB, która pokrywa się z obserwacjami L u k
a s h k i n a (1975), wykonanymi na szerokości geograficznej bliskiej
toruńskiej, oraz L a w r e n c e' a i in. (1964).
Ponieważ
tłumienie jonosfery rośnie z odległością zenitalną W pierwszym
przybliżeniu jak secans tego kąta, zatem biorąc średnią deklinację
Słońca ok. 20° na szerokości geograficznej Piwnic (53,1°) na
wartość tego tłumienia mogę ostatecznie przyjąć 0,035 dB. Odpowiada
mu czynnik korygujący 1,008, przez który należy mnożyć wyniki letnich
pomiarów strumienia promieniowania Słońca na częstości 127 MHz
(obserwacje radioźródeł kalibracyjnych wykonywane są w tym czasie w
nocy, a zatem praktycznie bez tłumienia).
T a b e l a 2
Refrakcja
atmosferyczna na częstości 127 MHz
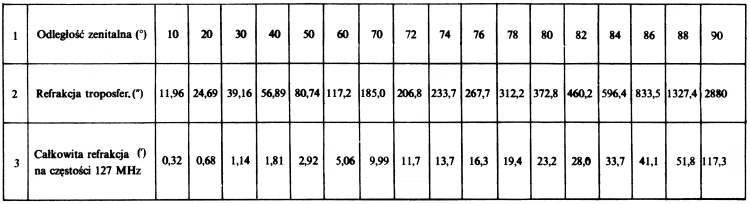
Wypada jeszcze raz podkreślić, że
rozpatrywane tłumienie jonosfery ulega dużym wahaniom, tak że
odchyłki od przyjętej tutaj wartości „średniej” mogą
nawet kilkakrotnie przewyższać tą wartość.
5. OSŁABIENIE REFRAKCYJNE
Wskutek istnienia refrakcji różnicowej
widome rozmiary kątowe źródeł kosmicznych maleją ze wzrostem ich
odległości zenitalnej z. Zjawisko to powoduje, że m.in.
pomiary strumienia promieniowania Słońca są systematycznie zaniżane o
czynnik (T r o i t s k i j 1959; T s e y t l i n 1976):
gdzie r(z) jest refrakcją
atmosferyczną. Średnią refrakcję na częstości 127 MHz obliczyłem wg
pracy K o l o s o v a i S h a b e l n i k o v a (1976) przyjmując,
że jej składnik zależny od częstości maleje z nią jak 1/f2
(np. E v a n s 1968). Tabela 2 zawiera wartości liczbowe dla
wybranych odległości zenitalnych, przy tym „refrakcja
troposferyczna” (składnik niezależny od częstości) dotyczy
refrakcji w warstwie atmosfery do wysokości 60 km.
Do wyliczenia współczynnika (10) użyłem
przygotowanego do innych celów dopasowania logarytmów wartości
refrakcji do wielomianu trzeciego stopnia (wykonanego szybką metodą
najmniejszych kwadratów przedstawioną przez D a v i d o n a (1977)).
W przybliżeniu tym refrakcję (w radianach) w zakresie wysokości h
= π/2 – z
od 0,035 do 1,1 radiana wyraża wzór:
|
r(h) = 0,01933·eh(6,79
– h(4,28 – 1,36·h)).
| (11) |
Dla wysokości od 46 do 60,5°
(odpowiadających wysokościom Słońca w Piwnicach w okresie maj –
sierpień) współczynnik niwelujący osłabienie refrakcyjne przyjmuje
wartości od 1,0016 do 1,0008, odpowiednio.
Ponieważ kalibracje toruńskich
obserwacji Słońca przeprowadza się za pomocą radioźródeł górujących
blisko zenitu, dla których zatem osłabienie refrakcyjne jest
zaniedbywalnie małe, to przyjęcie poprawki 0,l% do pomiarów
strumienia Słońca nie będzie stanowiło dużego odstępstwa od
rzeczywistości.
L I T E R A T U R A
B a a r s J.W.M., H a r t s u i j k e
r A.P., 1972, Astron. Astrophys., 17, 172.
B
a a r s J.W.M., G e n z e l R., P a u l i n y - T o t h I.I.K., W
i t z e l A., 1977, Astron. Astrophys, 61, 99.
B
e r k o w i t z R.S. (wyd.), 1965, Modern Radar – Analysis,
Evaluation and System Design, J. Wiley and Sons, N.Y.
B
e y n o n W.J.G. (wyd.), 1960, Some Ionospheric Results Obtained
During the IGY, Elsevier, Amsterdam.
B
e y n o n W.J.G.. W i l l i a m s P.J.S., 1978, Rep. Prog. Phys.,
41, 909.
B
i e l i k o v i c h V.V., B e n e d i k t o v E.A., T o l m a c h e
v a A.V. 1975, Geomagn. Aeron., 15, 251.
B
o r k o w s k i K.M., 1975, Post. Astr., 23, 199.
B
o r k o w s k i K.M., 1977, Post. Astr., 25, 135. .
B
o r k o w s k i K.M., 1980, Post. Astr., 27, 175
B
o r k o w s k i K.M., Z l o b e c P., Z a n e l l i C.A., 1980,
Mem. Soc. Astron. Ital., 51, 247.
B
r a c e w e l l R.N. (wyd.), 1959, Paris Symposium on Radio
Astronomy, Stanford (Calif.).
C
h i v e r s H.J.A., W e l l s H.W., 1959, J. Atmos. Terr. Phys.,
17, 13.
C
r a n e R.K., 1976, Meth. Exper. Phys., 12B, 136.
D
a v i d o n W.C., 1977, Am. J. Phys., 45, 260.
D
e n t W.A., A l l e r H.D., O l s e n E.T., 1974, Astrophys. J.,
188, L11.
E
l g a r ö y Ö., S l o t t j e C., T l a m i c h a A., U r b a r z
H., Z a n e l l i C., Z l o b e c P., B o u g e r e t J.-L., K e r
d r a o n A., de la N ö e J., 1980, Astron. Astrophys. Suppl., w
druku.
E
s s e x E.A., 1978, J. Atmos. Terr. Phys., 40, 1019.
E
v a n s J.V., 1968, w zbiorze: Evans, Hagfors 1968, 99.
E
v a n s J.V., H a g f o r s T. (wyd.), 1968, Radar Astronomy,
McGraw-Hill, N.Y.
F
o k k e r A.D., R o o s e n J., 1963, Het PTT – Bedrijf, 12,
80.
F
r i h a g e n J. (wyd.), 1966, Electron Density Profiles in
Ionosphere and Exosphere, North-Holland, Amsterdam.
G
n a n a l i n g a m S., K a n e J.A., 1978, J. Atmos Terr. Phys.,
40, 629.
G
r a f W., 1974, Solar Phys., 37, 257.
H
a g f o r s T., 1976, Meth. Exper. Phys., 12B, 119.
K
e l s o J.M., 1968, Radio Ray Propagation in the Ionosphere,
McGraw-Hill, N.Y.
K
o l o s o v M.A., S h a b e l n i k o v A.V., 1976, Refraktsiya
elektromagnitnykh voln v atmosferakh Zemli, Venery i Marsa, Sov.
Radio, M.
K
ö h n l e i n W., 1978, Rev. Geophys. Space Phys., 16, 341.
L
a w r e n c e R.S., L i t t l e C.G., C h i v e r s H.J.A., 1964,
Proc. IEEE, 52, 4.
L
e r f a l d G.M., P a r t h a s a r a t h y R., 1966, w zbiorze:
Frihagen 1966, 90.
L
u k a s h k i n V.M., 1975, Geomagn. Aeron., 15, 553.
M
i l l m a n G.H., 1965, w zbiorze: Berkowitz 1965, 317.
M
o n t b r i a n d L.E., B e l r o s e J.S., 1972, Radio Sci.,7,
133.
QBSA
(Quarterly Bulletin on Solar Activity), 1977-1979, IAU, Tokyo.
R
a n t a H., R a n t a A., 1977, J. Atmos. Terr. Phys., 39,_309.
R
a n t a H., R a n t a A., I978, J. Atmos. Terr. Phys., 40,
799.
R
a t c l i f f e J.A., 1972, An
Introduction to the Ionosphere and Magnetosphere,
Cambridge University Press.
R
a w e r K. (wyd.), 1976, Manual on Ionospheric Absorption
Measurements, Rep. UAG-57, WDC-A, Boulder (Color.).
S a r a d a K.A., M i t r a A.P.,
1960, w zbiorze: Beynon 1960, 270.
S c h u n k R.W., N a g y A.F., 1978,
Rev. Geophys. Space Phys., 16, 355.
S k r e b k o v a L.A., 1975, Geomagn.
Aeron., 15, 664.
T a y l o r G.N., 1966, w zbiorze:
Frihagen 1966, 543.
T r o i t s k i j V.S., 1959,
Radiofizika, 2, 683. .
T s e y t l i n N.M., 1976, Antennaya
tekhnika i radioastronomiya, Sov. Radio, M.
W a t e r s J.W., 1976, Meth. Exper.
Phys., l2B,,l42.
W h i t f i e l d G.R., 1959, w
zbiorze: Bracewell 1959, 297.
[Udostępnione: 3 II 2012 r.]



