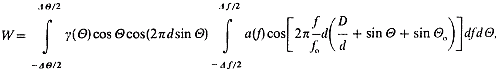POSTĘPY ASTRONOMII

Tom XXIX (1981). Zeszyt 2

 

 

ANALIZA  BŁĘDÓW  SYSTEMATYCZNYCH

W  TORUŃSKICH  POMIARACH  STRUMIENIA

RADIOWEGO  PROMIENIOWANIA  SŁOŃCA

 

 

Część  II

 

CZYNNIKI  INSTRUMENTALNE

 

 

K A Z I M I E R Z   M.  B O R K O W S K I

 

Katedra Radioastronomii Uniwersytetu M. Kopernika (Toruń)

 

(Otrzymano 24 lipca 1980 r.)

 

 

S t r e s z c z e n i e  — Przeprowadzono szczegółową dyskusję różnych czynników instrumentalnych wpływających na toruńskie pomiary strumienia promieniowania Słońca na częstości 127 MHz. Podano dokładne parametry toruńskiego interferometru. Z podsumowania współczynników korekcyjnych wynika, że w ciągu ostatnich 20 lat toruńskie wyniki były zawsze zaniżone o ponad 20%. Wybrane wyniki poprawiono na dyskutowane efekty, co doprowadziło do dobrej ich zgodności z rezultatami uzyskanymi gdzie indziej.

 

 

AN  ANALYSIS  OF  SYSTEMATIC  ERRORS  OF  THE  TORUŃ  SOLAR  RADIO FLUX  MEASUREMENTS.  Part  II.  INSTRUMENTAL  FACTORS.  S u m m a r y — Various instrumental effects having an influence on the Toruń total solar flux measurements at 127 MHz are discussed in detail. Accurate parameters of the Toruń interferometer are presented. A summary of correction coefficients shows that during the last 20 years the Toruń results were always lowered by more than 20%. Some observational data were corrected and found to be in good agreement with other observatories results.

 

W części I tej pracy (B o r k o w s k i 1981a) przedstawiłem analizę wpływu wzorców strumienia, eliptyczności orbity Ziemi oraz tłumienia w atmosferze ziemskiej na pomiary gęstości strumienia promieniowania Słońca. W tej części przeanalizuję systematyczne błędy takich pomiarów związane z metodą stosowaną w Toruniu przy obserwacjach interferometrycznych na częstości 127 MHz. Wynikają one z częściowego rozdzielenia Słońca (funkcja widzialności jest znacząco mniejsza od jedności), ze zdudniania się promieniowania radioźródeł kalibracyjnych, z niedokładności ustawienia anten i nieliniowości wzmocnienia odbiornika. Do oceny tych błędów potrzebna jest znajomość parametrów instrumentu, takich jak wielkość bazy interferometru, jej usytuowanie i orientacja w przestrzeni, tzw. zapóźnienie instrumentalne, charakterystyki anten i wzmocnienia odbiornika itp.

 

 

6. PARAMETRY SYSTEMU ODBIORCZEGO

 

Wielkość i orientację bazy interferometru zasadniczo można wyznaczyć z pomiarów fazy sygnału interferencyjnego, jeśli są znane współrzędne obserwowanego radioźródła punktowego (np. B o r k o w s k i 1980b). Idea ta jest szeroko wykorzystywana w praktyce (np. W a d e 1970; B r o s c h e  i in. 1973; E l s m o r e 1974). Duże dokładności wyznaczeń uzyskuje się głównie dzięki dużym bazom instrumentów (tysiące długości fali). Próby określenia niektórych parametrów małobazowego interferometru toruńskiego na podstawie istniejących zapisów obserwacji Słońca i radioźródeł kalibracyjnych prowadziły do wyników obarczonych zbyt dużymi błędami (wyrażonymi w rozrzucie rezultatów). Próby te wykonałem wszakże zaniedbując efekt refrakcji i traktując Słońce jako punktowe, co pozwala mieć nadzieję na lepsze w przyszłości rezultaty ściślejszych analiz. Piszę o tym dlatego, że metoda ta jest obecnie jedyną drogą odzyskania zadowalająco dokładnych parametrów toruńskiego interferometru, którym wykonywano dyskutowane tutaj obserwacje do roku 1972. Dla celów tej pracy z konieczności przyjmę, że baza tamtego interferometru miała długość dokładnie 10 λ i leżała dokładnie na linii wschód-zachód. Także błędy parametrów tego instrumentu cytowane w tab. 13 trzeba traktować jako orientacyjne.

 

Od jesieni 1972 r. w toruńskiej służbie Słońca używa się nowego, zbudowanego na miejscu starego, interferometru. Współrzędne i wielkość jego bazy zostały wyznaczone z pomiarów geodezyjnych przeprowadzonych w maju i czerwcu 1977 r. Szczegółowy opis i wyniki tych pomiarów przedstawiłem w swej pracy doktorskiej (B o r k o w s k i 1979). Tutaj, w tab. 3, podaję wybrane wyniki końcowe. Są one podstawą do prezentowanych niżej obliczeń. Przyjąłem w nich ponadto, że charakterystykę anten obecnego systemu odbiorczego dobrze przybliża cosinus w czwartej potędze kąta liczonego od kierunku maksimum wzmocnienia.

 

 

T a b e l a  3

 

Podstawowe parametry toruńskiego systemu odbiorczego

 

 

 

 

7. WIDZIALNOŚĆ SŁOŃCA

 

Amplituda przebiegu interferencyjnego zarejestrowanego w czasie obserwacji źródła rozciągłego o znormalizowanym rozkładzie temperatury jasnościowej , gdzie Γ jest rozkładem jasności (funkcją spójności) źródła, wyraża się wzorem (B o r k o w s k i 1980):

 

(12)

 

gdzie: zmienna Θ jest kątem na płaszczyźnie zawierającej źródło promieniowania i anteny, Θ_o wyznacza kierunek źródła i liczone jest od płaszczyzny prostopadłej do bazy interferometru d, ΔΘ jest całkowitą szerokością źródła, f – częstością fali, f_o – częstością środkową pasma odbieranych częstości, Δf – szerokością całkowitą tego pasma, a(f) = |A(f – f_o)|²/∫ _±∞|A(f)|²df, A(f) jest napięciową charakterystyką przenoszenia stopni wielkiej częstości, a D – zapóźnieniem instrumentalnym (λ). Dopełnienie amplitudy W (zwanej widzialnością listków interferencyjnych) do jedności wyraża względną stratę sygnału, wynikającą z częściowego rozdzielenia obserwowanego źródła i ze skończoności szerokości pasma odbieranych częstości.

 

Z praktycznych wyliczeń wynika, że w przypadku parametrów toruńskiego interferometru przy obserwacjach w pobliżu prawdziwego południa wpływ czynnika zależnego od częstości na wartość funkcji widzialności W jest przynajmniej o rząd mniejszy od niezaniedbywalnego. W celu oceny widzialności Słońca w tym przypadku wystarczy wzór przybliżony:

  

(13)

 

Wartości funkcji (13) przy założeniu różnych modeli rozkładu jasności Słońca zawiera tab. 4, zaś same modele przedstawia rys. 2, w którym oznaczenia krzywych pokrywają się z liczbami porządkowymi tejże tabeli. Obliczenia wykonałem za pomocą kalkulatora HP-25C, wykorzystując specjalnie przygotowany program całkowania numerycznego (B o r k o w s k i 1979).

 

Budując modele analityczne (1 – 5 w tab. 4) opierałem się na rzeczywistych rozkładach jasności spokojnego Słońca obserwowanych ostatnio na częstościach niezbyt odległych od toruńskiej. Z badań L a n t o s a  i  A v i g n o n a (1975) wynika, że na częstości 169 MHz szerokość rozkładu zmienia się od 31 (w minimum 11-letniego cyklu aktywności) do 36 – 37' (w maksimum). K u n d u  i in. (1977) stwierdzili, że w pobliżu ostatniego minimum szerokość ta na częstości 121,5 MHz wynosiła 33.9'.

 

Do niniejszej analizy rozkłady K u n d u  i in. oraz L a n t o s a  i  A v i g n o n a przeskalowałem arbitralnie do szerokości połówkowej 34' mając nadzieję, że odpowiada to rzeczywistości na częstości 127 MHz w czasach niezbyt odległych od minimów aktywności Słońca. Z tak przeskalowanego rozkładu K u n d u  i in. wybrałem 62 punkty, wykorzystując je do przybliżenia widzialności (13) odpowiednią sumą wartości dyskretnych. Do rozkładu L a n t o s a  i  A vi g n o n a zaś dopasowałem dwie funkcje analityczne (4 i 5 w tab. 4), tak by ograniczały rozkład rzeczywisty. Widzialność dla tego rozkładu widniejąca w tab. 4 jest średnią z widzialności obliczonych dla tych dwu dopasowanych funkcji.

 

Dysponując niewielką swobodą w wyborze widzialności pomiędzy wartościami odpowiadającymi modelom 6 i 7 w tab. 4 i biorąc pod uwagę fakt, że rozkład zaprezentowany przez K u n d u  i in. nie był uwolniony od wpływu skończonej szerokości charakterystyk promieniowania anten (nie wykonano

 

T a b e l a  4

 

Widzialność Słońca W obliczona dla interferometru toruńskiego.

Wielkość Θ_p jest szerokością połówkową modelowego

rozkładu jasności, a ΔΘ całkowitą jego szerokością

 

 

 

 

 

Rys. 2. Modelowe rozkłady temperatury jasnościowej Słońca na częstości 127 MHz

 

dekonwolucji), zdecydowałem dla częstości 127 MHz przyjąć wartość średnią, której odpowiada współczynnik korekcyjny 1/W = 1,022. Wynik ten znacząco przewyższa rezultaty wcześniejszych wyznaczeń (S o l e c k i 1974; B o r k o w s k i 1976a).

 

 

8. DUDNIENIA RADIOŹRÓDEŁ KALIBRACYJNYCH

 

Anteny toruńskiego systemu odbiorczego posiadają szerokie charakterystyki promieniowania, co powoduje, że w czasie obserwacji radioźródła kalibracyjnego odbierane bywa promieniowanie innych źródeł znajdujących się w polu widzenia. Skutkiem tego powstaje błąd w pomiarze strumienia obserwowanego źródła, który oczywiście przenosi się dalej na wyznaczenia strumienia promieniowania Słońca. Chociaż dość dawno zdano sobie sprawę z istnienia tego rodzaju błędu w toruńskich obserwacjach (np. B o r k o w s k i 1977), to dopiero szczegółowe studia modelowe pozwoliły na wiarogodne oceny ilościowe. Stanowią one istotę tego punktu pracy. Nazwa „dudnienia” ma odzwierciedlić charakterystyczny efekt zakłóceń uwidoczniający się na zapisach obserwacji interferometrycznych (por. rys. 4 i 5), a upodabniający go do zjawiska nakładania się dwóch fal o różnych częstościach.

 

Jeżeli w polu widzenia anten znajduje się jednocześnie kilka źródeł punktowych, to sygnał wyjściowy prostego interferometru ma postać (B o r k o w s k i 1980b):

 

(14)

 

gdzie – oprócz dotychczasowych oznaczeń – S_i jest gęstością strumienia i-tego źródła, G – napięciową charakterystyka promieniowania anten (tutaj w szczególności G = cos²(Θ_i – Θ_A), a TŁO grupuje wszystkie przyczynki do sygnału wyjściowego pochodzące ze źródeł rozciągłych (w tym szumy własne systemu odbiorczego). Uwzględniając trójwymiarowość przypadku, odległość kątową źródła o współrzędnych równikowych t_i i δ_i od kierunku maksimum wzmocnienia anten t_A i δ_A wyraża Θ _i – Θ_A = arccos[sinδ_i sinδ_A + cosδ_i cosδ_A cos(t_i – t_A)]. Podobnie: sinΘ_i = sinδ_osinδ_i + cosδ_o cosδ_i cos(t_i – t), gdzie wskaźnik o odróżnia współrzędne bieguna interferometru.

 

Czułość toruńskiego systemu odbiorczego jest taka, że oprócz tła (TŁO) niezaniedbywalne są tylko trzy radioźródła stałe: Słońce, Cas A i Cyg A. W przypadku, gdy kalibrację wykonuje się w czasie, kiedy Słońce jest już niewidoczne (okres letni), to suma występująca w (14) upraszcza się do tylko dwóch składników odpowiadających źródłom Cas A i Cyg A. Na czas obserwacji jednego z nich anteny ustawia się tak, by w momencie tranzytu źródło to przechodziło przez maksimum wzmocnienia. Można więc kierunkowi anten przypisać kąt godzinny t_A = 0° i deklinację obserwowanego źródła δ_A = δ₁.

 

Sygnał rejestrowany w czasie obserwacji pierwszego źródła można teraz przepisać w postaci zależności od kąta godzinnego t tego źródła:

 

S(t) = S1 (sin2δ1 + cos2δ1cost) 4cos2{πd[sinδosinδ1 + cosδocosδ1cos(t – to) +                                + D/d]} + S2[sinδosinδ2 + cosδocosδ2cos(t – Δα)]4·            ·cos2{πd[sinδosinδ2 + cosδocosδ2cos(t + Δα – to) + D/d]} + TŁO,

(15)

 

gdzie wskaźniki 1 i 2 dotyczą odpowiednio obu źródeł kalibracyjnych (celowo opuściłem wskaźnik 1 przy t, rezerwując to oznaczenie do innego określenia), a Δα jest różnicą rektascensji źródła zakłócającego (2-go) i obserwowanego.

 

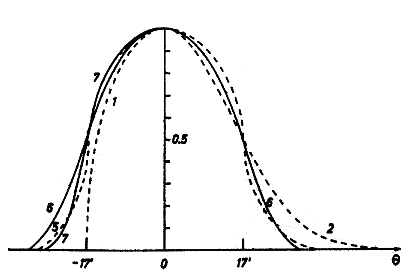
Dotychczasowa kalibracja toruńskiego systemu polegała na pomiarze wysokości głównego listka interferencyjnego obserwowanego źródła, której przypisywało się całkowity strumień S₁ tego źródła (jest to w przybliżeniu równoważne położeniu w (15) S₂ = 0). W rzeczywistości, jak wynika z prostej analizy geometrii pomiaru (rys. 3), wysokości tej odpowiada strumień:

 

 

Rys. 3. Szkic sposobu pomiaru strumienia promieniowania radioźródła

kalibracyjnego w głównym listku interferencyjnym

 

 

 

(16)

 

gdzie t₁ i t₃są kątami godzinnymi pierwszego źródła (albo odpowiednimi momentami czasu), przy których wypadają punkty styczności prostej łączącej sąsiadujące z głównym listkiem minima interferencyjne, zaś t₂ jest odpowiednim kątem (momentem) wyznaczonym dla maksimum głównego listka przebiegu S(t). Wyniki obserwacji Słońca obliczone bez uwzględniania obecności drugiego źródła wymagają więc korekty o (pomnożenia przez) czynnik S'₁/S₁.

 

Obliczenia współczynnika S'₁/S₁, przy pomocy wzorów (15) i (16) przeprowadziłem na maszynie cyfrowej Riad 32 (B o r k o w s k i 1979), przyjmując parametry interferometru podane w tab. 3 i odpowiadające antenom skierowanym na zenit. Współrzędne radioźródeł Cas A i Cyg A zaczerpnąłem z pracy B a a r s a (1973), procesję obliczyłem wg algorytmów podanych u B e r t i n a (1977) zaś strumienie przyjąłem takie same jak w części I tej pracy. Przykładowy model obserwacji Cas A zawiera rys. 5. Został on wygenerowany wg wzoru (15), w którym TŁO zaniedbano dla przejrzystości, z rozdzielczością czasową 2 min słonecznych. Rysunek ten dobrze oddaje zakłócający wpływ drugiego źródła (Cyg A), co się również dobrze zgadza z rzeczywistością. Dla porównania na rys. 4 przedstawiłem fragment zapisu obserwacji Cas A. Dolne obramowanie tego rysunku pokrywa się z poziomem minimum tła galaktycznego w ciągu doby. Warto zauważyć, że po wschodzie Słońca obserwacja ta jest trochę zakłócona, gdyż Słońce w tym dniu było aktywne.

 

Wyniki obliczeń współczynników korekcyjnych zawiera tab. 5 i rys. 6. Zostały one uzyskane przy założeniu, że w pobliżu momentu tranzytu Cyg A obserwowane tło galaktyczne jest jednostajne (co odpowiada położeniu: TŁO = const), zaś w chwili górowania Cas A – monotonicznie malejące z szybkością dwóch strumieni Cyg A na radian kąta godzinnego. Uwzględnienie zmienności tła wprowadza tylko nieznaczne zmiany w końcowych wynikach. Błąd obliczonych współczynników oceniłem metodą różniczki zupełnej, przyjmując niepewności parametrów podane w tab. 3 oraz kładąc na niepewność stosunku strumieni radioźródeł kalibracyjnych, zarówno S₂/S₁ jak S₁/S₂, błąd 0,07.

 

Ponieważ podstawowym źródłem sygnału porównawczego przy kalibracjach obserwacji Słońca w Toruniu była i jest (z powodu większego strumienia) Cas A, zatem trzeba przyjąć, że wszystkie wyniki opracowane od roku 1960 są zaniżone tylko z powodu omawianego teraz czynnika o 22 – 26%. Chciałbym jeszcze zwrócić uwagę na to, że ocena błędu wynikającego z dudnień radioźródeł kalibracyjnych w latach l960 – 1972 jest tylko orientacyjna, gdyż przy obliczeniach dla tego okresu przyjąłem takie same charakterystyki promieniowania anten, jak w okresie późniejszym. Wiadomo jednak, że były one węższe, co oznacza, że błędy są w rzeczywistości mniejsze. Nie jest to wszakże wielkie zmartwienie, ponieważ w chwili, gdy owa charakterystyka będzie znana dostatecznie dokładnie i będą znane dokładniej parametry tamtego i interferometru, będzie można powtórzyć obliczenia po niekłopotliwych modyfikacjach istniejących już programów (są one napisane w języku FORTRAN IV).

 

 

Rys. 4. Przykładowy fragment toruńskiego zapisu

interferometrycznej obserwacji Cas A

 

 

 

Rys. 5. Komputerowa symulacja dudnień w czasie obserwacji Cas A przy pomocy toruńskiego interferometru. Czas liczony jest od momentu górowania Cas A. Skalę intensywności wyrażono w jednostkach strumienia Cas A.

 

 

T a b e l a  5

 

Współczynniki korekcyjne S'_i/S_i wynikające z dudnień radioźródeł

kalibracyjnych obserwowanych toruńskim interferometrem

 

 

 

 

 

 

Rys. 6. Współczynnik korekcyjny do obserwacji toruńskich wynikający

z dudnień radioźródeł kalibracyjnych w latach 1960 – 1985

 

 

 

9. ROZBIEŻNOŚĆ KIERUNKÓW MAKSIMUM WZMOCNIENIA

ANTEN I GŁÓWNEGO LISTKA INTERFERENCYJNEGO

 

Głównemu (albo centralnemu) listkowi interferencyjnemu zapisu obserwacji Słońca przypisuje się wagę jednostkowa rozumiejąc, że jego kierunek pokrywa się z kierunkiem maksimum wzmocnienia anten. W obecnym toruńskim interferometrze główny listek pojawia się ok. 12 min. po górowaniu Słońca, a zatem ok. 3° na zachód od południka. Łatwo stąd obliczyć poprawkę ok. 0,6%. W czasie obserwacji Cas A główny listek występuje kilka minut przed górowaniem tego źródła, co oznacza zmniejszenie owej 0,6% poprawki.

 

Ze względu na to, że kierunek maksimum wzmocnienia anten nie jest wystarczająco dokładnie znany, byłoby przedwczesne wprowadzenie omówionej tu poprawki. Warto jednak zapamiętać, że czynnik ten w toruńskim przypadku praktycznie zawsze działa w kierunku zaniżania wyników pomiarów strumienia promieniowania Słońca.

 

 

 

10. ROZBIEŻNOŚĆ WIĄZEK ANTENOWYCH

 

Gdyby kierunki maksimum wzmocnienia anten interferometru nie pokrywały się (przypadek zwichrowania płaszczyzn, w których następuje zmiana nachylenia anten), to – przy prawidłowym spoziomowaniu anten – główny listek interferencyjny miałby wagę (rozumianą jako czynnik, przez który trzeba pomnożyć wynik pomiaru strumienia w tym momencie) większą od jedności; tym większą im większa byłaby odległość) zenitalna kierunków. Wyrażę to ściślej: jeśli charakterystykę napięciową każdej z anten oznaczyć przez G(Θ), to owa waga będzie równa 1/[G(0)G(ΔΦ)], a w toruńskim przypadku – cos²ΔΦ, gdzie różnica ΔΦ wyraża rozbieżność kierunków anten.

 

Nie ma podstaw, by wątpić w poprawne spoziomowanie anten toruńskiego interferometru (wiązki charakterystyk są równoległe przy nachyleniu ok. 90°). Jest wszakże wielce prawdopodobne, że przy nachyleniu bliskim poziomowi (0°) rozbieżność ich kierunków maksymalnych wzmocnień wynosi 3 – 5° (B o r k o w s k i 1979). Uczyniłoby to błąd 0,3 – 0,8% w czasie obserwacji przy horyzoncie. Dość szybko maleje on jednak ze wzrostem nachylenia anten, tak że przy wysokościach obserwowanych źródeł większych od 45° jest wszędzie mniejszy od 0,4%. Uwzględniając fakt, że podana rozbieżność wiązek nie została ostatecznie dowiedziona, ze spokojnym sumieniem można i ten czynnik zaniedbać; zapamiętać wszakże warto, że działa on w kierunku zaniżania wyników pomiarów.

 

 

 

11. SKOKOWE ZMIANY NACHYLENIA ANTEN

 

Wyznaczanie dziennej wartości strumienia promieniowania Słońca w obserwacjach toruńskich odbywa się przez uśrednienie pomiarów strumienia wykonanych w momentach maksimów listków interferencyjnych. Ponieważ anteny są nieruchome, zachodzi potrzeba różnego ważenia tych pomiarów przed uśrednieniem. O wadze przypisanej danemu listkowi decyduje przede wszystkim charakterystyka kierunkowa anten.

 

Z faktu, że deklinacja Słońca zmienia się w sposób ciągły, a nachylenie anten zmieniane jest skokowo, wynika, że również wagi wszystkich listków ulegają podobnym zmianom (droga, jaką przebywa Słońce w ruchu dziennym na tle charakterystyki anten jest codziennie inna). Wyznaczenie wag, które uwzględniałyby te niewielkie zmiany jest praktycznie niemożliwe, ale też i niecelowe. Doświadczenie wskazuje bowiem, że w toruńskim przypadku zmiany ustawienia anten co 6° deklinacji Słońca są niezauważalne w tle fluktuacji wyników. Łatwo wszakże widzieć, że mimo to sytuacja taka prowadzi do systematycznego zaniżania wyników pomiarów.

 

W szczególnym przypadku głównego listka interferencyjnego w skrajnych sytuacjach (w czasie przestawiania anten) Słońce jest odległe o 3° od kierunku maksimum wzmocnienia anten. Oznacza to także, że wtedy odbierany strumień Słońca jest dodatkowo osłabiony o ok. 0,55%. Na błąd w całym okresie między kolejnymi przestawieniami anten można przyjąć błąd średni całkowy, który wynosi nieco powyżej 0,2%. Nietrudno jest też pokazać, że w przypadku obecnego toruńskiego interferometru im bardziej listek interferencyjny jest odległy od centralnego tym mniejszy jest omawiany błąd.

 

 

 

12. ODBICIA

 

Charakterystykę fenomenologiczną i podłoże teoretyczne odbić promieniowania Słońca od gruntu przed antenami przedstawiłem już stosunkowo szeroko wcześniej (B o r k o w s k i 1977). Z materiału tam przedstawionego wynika m.in., że odbicia wywołują modulację wyników pomiarów strumienia, która ma roczną powtarzalność i że najmniejszy ich wpływ powinien się objawiać w okresie letnim. Jest tam też uwaga o obserwowanej wyraźnej (ok. 10%) depresji strumienia W okresie letnim przypisanej zjawisku odbić.

 

Obecnie skłonny jestem wspomniana depresję tłumaczyć zawyżeniem (wskutek odbić) strumienia w okresach bezpośrednio sąsiadujących z omawianym i wpływem niektórych z czynników omawianych już w tej pracy. Taka zmiana stanowiska umożliwia wyznaczenia bezwzględnych strumieni Słońca z toruńskich pomiarów wykonanych w okresie maj – sierpień, dlatego zachodzi potrzeba bliższego uzasadnienia.

 

Proponuję wrócić jeszcze raz do rys. 6 – 9 ze wspomnianej pracy i zwrócić uwagę na fakt, że owe umowne 10% depresji było oceniane względem maksimów w marcu – kwietniu i wrześniu – październik, kiedy to obserwacje dowodnie kłócą się z modelem (rys. 7, tamże). Jeśli dołączyć do tego kilka procent osłabienia letniego wynikającego z eliptyczności orbity ziemskiej, to już nietrudno wytłumaczyć niewielkie obserwowane zaniżenie wyników w czerwcu i lipcu i przystać – mam nadzieję, że również Czytelnikowi – na nową interpretację.

 

Opierając się na powyższej argumentacji od teraz będę zakładał, że w okresie maj – sierpień wpływ odbić na obserwacje jest zaniedbywalny. W pozostałych częściach roku wpływ ten jest niekiedy bardzo silny i nieregularny – prawdopodobnie na skutek zmian pogody (głównie wilgotność gruntu, która decyduje o wartości współczynnika odbicia fal elektromagnetycznych). Na szczęście w tych zakłóceniach odbioru wyróżnia się pewien składnik wolnozmienny o dość ustalonym charakterze. Pozwoli to na przynajmniej statystyczne poprawienie wyników z obserwacji wykonanych rok lub więcej wstecz (poprzez wyrugowanie tego składnika).

 

Istnienie zjawiska odbić uzasadnia ograniczenia oceny niektórych przedstawionych w tej pracy poprawek do pomiarów jedynie do okresu letniego. Wspomniana wyżej procedura statystycznego usuwania wpływu odbić w pozostałych porach roku uwzględni automatycznie wszystkie inne czynniki brane pod uwagę przy pomiarach letnich.

 

 

 

13. CHARAKTERYSTYKA WZMOCNIENIA ODBIORNIKA

 

 

I. PRZYPADEK DUŻYCH SYGNAŁÓW

 

Charakterystykę wzmocnienia toruńskiego odbiornika analizowałem na tych łamach wcześniej (B o r k o w s k i 1980a, d). Z tej analizy wynikało, że np. w okresie XII 1975 – X 1976 charakterystykę tę najlepiej przybliżało wyrażenie:

 

TG = 4619 U/(503,1 – U)2,

(17)

 

gdzie: T_G jest sygnałem z generatora szumów podawanym na wejście odbiornika (w jednostkach temperatury otoczenia T_o(K)), a U odpowiadającym mu napięciem wyjściowym (w mm wychylenia samopisu). W tym okresie charakterystykę przybliżano funkcją logarytmiczną dopasowywaną w dolnych rejonach. Najlepiej

pasująca w ten sposób do (17) funkcja tego typu ma postać (B o r k o w s k i 1980d):

 

TG = 2,01 exp(U/113,3) – 2.

(18)

 

Łatwo z powyższego wyliczyć, że przy sygnałach rzędu 100T_o (co odpowiada gęstości strumienia ok. 1000 su; 1 su = 10^-22 Wm^–2Hz^–1) wzór (18) daje temperaturę o ok. 50% mniejszą niż (17). Błąd ten rośnie ze wzrostem sygnału wejściowego.

 

 

II. PRZYPADEK MAŁYCH SYGNAŁÓW

 

Od stycznia 1974 r. w przypadku, gdy Słońce było spokojne lub o niewielkiej aktywności (sygnał do ok. 8T_o), charakterystyka odbiornika była przybliżana funkcją odcinkami liniowa. Odcinki te mieściły się pomiędzy punktami pomiarowymi odległymi o 0,5T_o. Taka procedura była uzasadniona niepewnością samej charakterystyki i metodyką opracowania danych (za pomocą minikomputera). Oczywiście, przybliżenie to obarczone jest pewnym błędem, który w tym miejscu ocenię, przyjmując, że wzór (18) w obszarze małych sygnałów dobrze odzwierciedla charakterystykę rzeczywistą (co istotnie ma miejsce).

 

Niech charakterystykę odbiornika opisuje ogólne wyrażenie:

 

U = α ln(T/β),

(19)

 

a pomiędzy punktami U_j(T_j) i U_j+1(T_j+1) niech będzie ona przybliżona przez funkcję liniową:

 

U’ = (T – Tj) (Uj+1 – Uj)/(Tj+1 – Tj)

(20)

 

Sytuację taką ilustruje rys. 7 w przypadku, gdy j = 1.

 

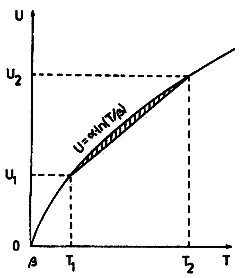
Rys. 7. Ilustracja do dyskusji błędu powstającego wskutek liniowego

przybliżenia logarytmicznej charakterystyki odbiornika

 

 

Średnia odchyłka temperatury wynikającej z przyjętego przybliżenia liniowego od rzeczywistej na odcinku pomiędzy U_j i U_j+1 wynosi:

 

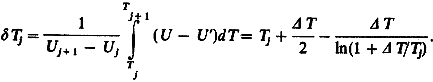(21)

 

gdzie ΔT = T_j+1 – T_j.

 

Można pokazać (P a z d e r s k i 1979), że lim_Tj→∞ δT_j  = 0. Istotniejsze wszakże jest to, że błąd δT_j szybko maleje ze wzrostem T_j, tak że dla dużych sygnałów jest praktycznie zaniedbywalny. Przyjmując, że tak jak w Toruniu, T_j = 1,5 + 0,5j, j = 1, ..., 16 prosto znajduję np. δT₁ = 2 + 0,5/2 – 0,5/ln 1,25 = 0,0093, δT₂ = 0,0076 i δT₁₅ = 0,0023.

 

Ponieważ sygnał mierzony ujawnia się jako różnica dwóch poziomów, z których każdy obarczony jest pewnym błędem, to błąd pomiaru jest kombinacją tych pierwszych. Jeżeli różnica poziomów odpowiadająca sygnałowi jest całkowitą wielokrotnością odstępu przybliżeń (mΔT), to średni błąd względny dyskutowanego tutaj przybliżenia wynosi:

 

(δTj – δTj+m)/( mΔT)

(22)

 

Gdy sygnał nie spełnia wymienionego warunku, błąd ten mieści się w granicach pomiędzy błędami obliczonymi zgodnie z (22), ale dla dwóch sąsiadujących poziomów (j i  j + 1 lub m + j i m + j + 1). Przekonuje o tym doświadczenie myślowe przeprowadzone dla przypadku sygnałów odpowiadających różnicy (m + 0,5)ΔT gdzie tak jak wyżej m jest liczbą całkowitą.

 

Przy obserwacjach Słońca spokojnego, kiedy jego strumień powoduje przyrost sygnału rzędu 0,5T_o na tle znajdującym się w pierwszym przedziale przybliżenia (okres letni), błąd pomiaru wyrażony wzorem (22) wynosi (δT₁ – δT₂)/0,5 = 0,0034, zaś w czasie wzmożonej aktywności (sygnał rzędu 7T_o) –  (δT₁ – δT₁₅)/7 = 0,001.

 

Podczas obserwacji radioźródeł kalibracyjnych błąd liniowego przybliżenia był o około rząd mniejszy dzięki zawężeniu przedziałów ΔT do 0,1T_o i z powodu wyższego tła, na którym są te źródła obserwowane. Powoduje to, że dopiero co obliczony błąd przenosił się wprost na wyniki pomiaru promieniowania Słońca. Dodać warto, że od jesieni 1978 r. w Toruniu zaniechano przybliżenia odcinkami liniowego zastępując go przybliżaniem funkcjami ciągłymi.

 

 

14. PODSUMOWANIE

 

Wszystkie przedyskutowane tutaj i w części I (B o r k o w s k i 1981a) niniejszej pracy czynniki, wpływające w sposób systematyczny na wyniki toruńskich pomiarów gęstości strumienia promieniowania Słońca na częstości 127 MHZ, zebrałem w tab. 6. W kolumnie „ogólnie” figurują orientacyjne informacje o wartościach liczbowych odpowiednich współczynników, korekcyjnych oraz przybliżona poprawka na czerwiec 1961 r. W pozostałych kolumnach umieściłem szczegółowe współczynniki obliczone dla okresów wybranych z ostatnich kilku lat, do których odnoszą się specjalnie wykonane obserwacje Słońca na falach metrowych przeprowadzone w innych obserwatoriach.

 

W poprawce na skale strumienia w latach 1975 i 1976 dodatkowo uwzględniłem błąd gruby, wynikający z mylnego przyporządkowania wagi jednostkowej listkowi niecentralnemu (prowadzącego do zawyżenia tamtych wyników o ok. 4%).

 

W końcu 1976 r. uległ awarii generator szumów, który służył od kilku lat do kalibracji toruńskiego odbiornika. W związku z tym później nie zmieniono dotychczas wypracowanego nawiązania do radioźródeł kalibracyjnych, ograniczając się do okresowych kontroli stabilności systemu odbiorczego. Stąd bierze się przypisanie niższych, niż wynika z tab. 5, współczynników korekcyjnych związanych z dudnieniami w okresach po roku 1976.

 

Okres z 1975 r. obejmuje dni od 25. V do 1 VI – te same, do których odnosi. się praca K u n d u  i in. (1977). W 1976 r. podobne obserwacje wykonali E r i c k s o n  i in. (1977) w dwóch okresach bezpośrednio sąsiadujących z ostatnim minimum 11-letniej aktywności Słońca: 16-23 VII i 18-21 VIII (toruńskiego pomiaru z dnia 18 VIII nie uwzględniłem stwierdzając, że odpowiadał on Słońcu aktywnemu). W dniach 17 – 25 VII 1978 r. jednorazowe obserwacje wykonali A l v a r e s  i  Y u r o v s k y (1979). Wreszcie współczynniki na dzień 12 V 1979 r. obliczyłem dla potrzeb grupy roboczej powołanej do studiów burz szumowych (E l g a r ö y  i in. 198l).

 

Dostępne w dziennikach obserwacji średnie dzienne gęstości strumienia na częstości 127 MHz z wyżej wymienionych okresów uśredniłem i poprawiłem zgodnie z podanymi współczynnikami. Wyniki te mieszczą się w ostatnich wierszach tab. 6. Cytowane tam błędy są odchyłkami standardowymi od średnich. Dyskusję tych rezultatów w kontekście ze wspomnianymi już innymi wyznaczeniami przedstawiłem gdzie indziej (B o r k o w s k i 1979, 1981b). Wynika stamtąd m.in., że szczytowa temperatura jasnościowa spokojnego Słońca w ostatnim minimum aktywności (1976 r.) na częstości 127 MHz nie zeszła poniżej 9 × 10⁵ K.

 

Od wielu lat znane są rozbieżności wyznaczeń strumienia promieniowania Słońca wykonanych na pobliskich częstościach zakresu fal metrowych (i nie tylko) w różnych stacjach. Niezgodności toruńskich wyników z innymi w ostatnich latach w przypadku spokojnego Słońca oceniłbym na ok. 30% (por. np. D u l k  i in. 1977 lub E r i c k s o n  i in. 1977). Niniejsze opracowanie w znacznym stopniu wyjaśnia ten problem. Główny winowajca okazuje się kryć w metodyce kalibracji obserwacji opartej na nawiązywaniu pomiarów do strumieni radioźródeł Cas A i Cyg A (dudnienia). Pozostałe przyczynki, acz same małe, w sumie składają się na blisko 10-procentowe zaniżenie wyników końcowych.

 

Uwzględnienie współczynników korekcyjnych opisanych w tej pracy sprowadza toruńskie obserwacje do stanu dobrej zgodności z najlepszymi wyznaczeniami wykonanymi doskonalszymi technikami (por. rys. 8) (B o r k o w s k i 1981b). Zgodność tę można zamknąć w kilku (5 – 7) procentach. Wierzę, że taka jest też dokładność tych obserwacji w stosunku do wartości bezwzględnych w przypadku kilkudniowych serii pomiarów spokojnego Słońca.

 

T a b e l a  6

Współczynniki korekcyjne do kalibracji bezwzględnych

toruńskich obserwacji Słońca. na częstości 127 MHz

 

 

 

 

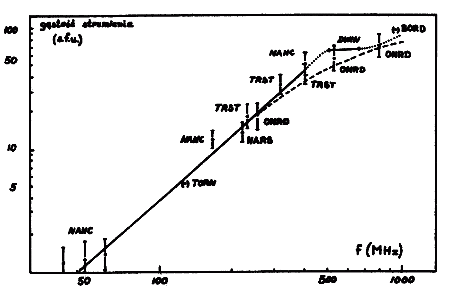
Rys. 8. Widmo promieniowania Słońca na falach metrowych w dniu 12 V 1979 r. (wg E l g a r ö y a  i in. 1981). Skalę gęstości strumienia wyrażono w jednostkach słonecznych (su), a czteroliterowe skróty są oznaczeniami stacji zgodnie z konwencją Światowych Centrów Danych (WDCs) (TORN jest skrótem Obserwatorium Toruńskiego). Linią przerywaną zaznaczone jest widmo spokojnego Słońca wg Smerda (1964)

 

 

Kilka wcześniejszych prac (B o r k o w s k i  i in. 1975, B o r k o w s k i  1976a, b, 1977) bez zmian oraz treść tego i kilku poprzedzających go artykułów (B o r k o w s k i 1980a, b, c, d, 1981a, b,  B o r k o w s k i   i in. 1980) stanowiły przedmiot obrony mojej pracy doktorskiej na Wydziale Matematyki, Fizyki i Chemii Uniwersytetu M. Kopernika w Toruniu w dniu 11 marca 1980 r.

 

 

L I T E R A T U R A

 

A l v a r e s  O., Y u r o v s k y  Yu. F., 1979, Solnechnye Dannye, 2, 104.

B a a r s  J. W. M., 1973, IEEE Trans. Antennas Prop., 21, 461.

B e r t i n  F. C., 1977, Programmes for Pocket Calculators HP-67 and HP-97 in the Fíeld of Theoretical and Observational Astronomy, Leuven University Press, Leuven.

B o r k o w s k i K. M., 1976a, Post. Astr., 24, 15. 

B o r k o w s k i K. M., 1976b, Post. Astr., 24, 115.

B o r k o w s k i K. M., 1977, Post. Astr., 25, 135.

B o r k o w s k i K. M., 1979, praca doktorska UMK, Toruń.

B o r k o w s k i K. M., 1980a, Post. Astr., 28, 15.

B o r k o w s k i K. M., 1980b, Post. Astr., 28,79.

B o r k o w s k i K. M., 1980c, Post. Astr., 28, 175.

B o r k o w s k i K. M., 1980d, Post. Astr., 28, 315.

B o r k o w s k i K. M., 1981a, Post. Astr., 29, 55.

B o r k o w s k i K. M., 1981b, Solar Phys., w druku.

B o r k o w s k i K. M., G o r g o l e w s k i  S., U s o w i c z  J., 1975, Post. Astr., 23, 141.

B o r k o w s k i K. M., Z l o b e c P., Z a n e l l i C. A., 1980, Mem. Soc. Astr. Ital., 51, 247.

B r o s c h e  P., W a d e C. M., H j e l l m i n g  R. M., 1973, Astrophys. J., 183, 805.

D u l k  G. A., S h e r i d a n  K. V., S m e r d  S. F., W i t h b r o e G. L., 1977, Solar Phys., 52, 349.

E l g a r ö y Ó,, S l o t t j e C., T l a m i c h a A., U r b a r z H., Z a n e l l i C., Z l o b e c P., B o u g e r e t J. L., K e r d r a o n A., de la N o ë J., 1981, Astron. Astrophys., Suppl., Ser., 44, 165.

E l s m o r e B., 1974, w New Problems in Astrometry (wyd. W. Gliese i in.), str. 111, Reidel, Dordrecht - Holland.

E r i c k s o n W. C., G e r g e l y T. E., K u n d u M. R., M a h o n e y M. J., 1977, Solar Phys., 54, 57.

K u n d u M. R., G e r g e l y T. E., E r i c k s o n W. C., 1977, Solar Phys., 53, 489.

L a n t o s P., A v i g n o n Y., 1975, Astron. Astrophys., 41, 137.

P a z d e r s k i E., 1979, informacja osobista.

S m e r d S. F., 1964, Ann. of the IGY, 34, 331.

S o l e c k i T., 1974, praca magisterska UMK, Toruń.

W a d e C. M., 1970, Astrophys. J., 162, 381.