Chapter II

RT32 — K. Borkowski, Z. Bujakowski

(Last updated: 2004.02.23)    

II.1  The Construction

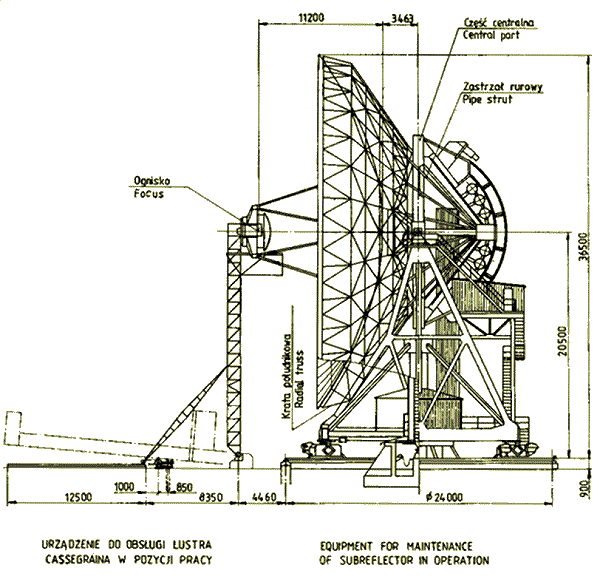
Fig. II.1: Design scheme of the 32-meter radio telescope – maintenance state view (Z. Bujakowski, Materiały V Kraj. Symp. Nauk Rad., Toruń 1987, part II, p. 66)

The antenna is a fully steerable telescope with horizontally mounted main parabolic reflector, 32 m in diameter, and working in classical Cassegrain mode, the 3.2 m in diameter secondary mirror being a removable hyperboloid of revolution. The main reflector is made up of 336 panels arranged in seven concentric rings. Accordingly, there are seven different panels, all of them having the same length (2.24 m) but width (1.2 ÷ 1.6 m) and shape varying according to the ring they belong. The reflecting surface is made of aluminium sheet, 2.5 mm thick, riveted to an aluminium frame made of T-shaped rails. The sheets have been shaped into a section of the paraboloid of revolution coarsely by mechanical stretching on special hooves and finally adjusted with the help of 39 screws mounted so as to be able to finely deform the underlying frame. The measured mean square deviation of the panel surface from the pefect paraboloid is smaller than 0.35 mm. The panels are fixed to the telescope structure with four adjustable screws at their corners. Measurements made with a laser rangefinder after final adjustments of the panels have shown that they are set relative to each other with an accuracy of 0.2 mm.

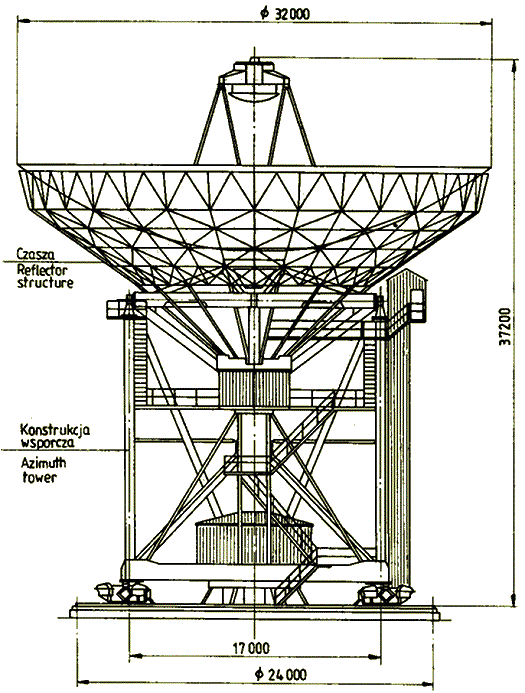Fig. II.2: Design scheme of the 32-meter radio telescope – rest state view (Z. Bujakowski, Materiały V Kraj. Symp. Nauk Rad., Toruń 1987, part II, p. 66)

The telescope can move around two perpendicular axes: fixed vertical and movable horizontal. The position and speed of the antenna relative to these axes is measured with absolute precision of 0.001° with the help of 19-bit angle converters mounted directly on the axes. In order that telescope movements are smooth and continuous all drives are doubled and work in the so called antibacklash mode (when one motor pulls, the other brakes with 10 % of the nominal force of 27.5 Nm).

Gravity distorts the surface figure of the telescope and changes position and orientation of the secondary mirror which, especially at higher observing frequencies, may become unacceptable. Temperature variations and wind can also add to deformation of the figure of the dish. There are two principal ways to compensate for these distortions. One is special design of the dish support structure (so called homogenous structure) and the other makes use of the possibility to move the secondary mirror (which has four degrees of freedom). Altogether, the steering system consists of 8 motors in azimuth axis, 4 in elevation axis and 4 for driving the Cassegrain mirror. Naturally, it incorporates also a computer (HP435rt), number of electronic drivers, controllers and switches.

The entire construction of the telescope rests on four two-wheelers (wheels are 1.25 m in diameter) that move along a circular rail of 24 m in diameter.

Technical data of the 32 m radio telescope Type steerable parabolic antenna  Mount alt-az  Optics up to about 1 GHz prime focus — above about 1 GHz Cassegrain system  Rail track diameter 24.0 m Maximum height (above foundation) 37.6 m Panels: number (7 rings) 64+64+64+64+32+32+16 = 336 — size 224×(120 ÷ 160) cm Accuracy of manufacturing of the panels (rms) < 0.35 mm — of panels setting with the help of a templete (rms) 1.0 mm — of surface adjustment with a laser ranger and theodolite (rms) 0.2 mm — of fabrication of the subreflector (rms) 0.05 mm — of alignment of the subreflector axis with the paraboloid (max) 0.1 mm — of track leveling (max) 0.3 mm — of elevation axis leveling (max) 0.3 mm Gravitational deformation (dish edge; max) 4.2 mm Homology imperfections at the zenith (rms) 0.11 mm — — — — horizon (rms) 0.14 mm Elevation sky coverage +2 ÷ +95 ° Azimuth range (origin at South) ±270 ° Range of motion of the subreflector along the axis ±60 mm — of rotation of the subreflector around two axes ±5 ° Velocity in the elevation axis 0.004 ÷ 14.7 °/min — — — azimuth axis 0.008 ÷ 31 °/min Accuracy of tracking (both axes) 0.002 ° Aperture blockage by the subreflector and its supports 7.44 % Total weight on the rail track ~620 t Weight on the elevation axis bearings (including counterbalancing: ~90 t) ~320 t — of electrical devices ~2 t — of central cabin apparatus (under the antenna) 9.4 t — of steel rails (180 mm in width) 42.5 t — of the structure for maintenance of the subreflector ~16 t Operating wind velocity 16 m/s Survival wind velocity 56 m/s Maximum ice coverage 2 cm — temperature range –25 ÷ +35 °C

In practice, all observational work is carried out with the Cassegrain system, which uses a hyperbolic secondary mirror placed between the prime focus and paraboloid vertex. Cosmic radiation reflected from the paraboloid and then from the secondary mirror is collected in the secondary focus, which is one of the two foci of the hyperbolic mirror. Here, near the secondary focus, proper antennas (feeds) and receivers are placed. Since observations are made in many widely spaced frequency bands, many receivers and feeds are necessarily being mounted in the secondary focal plane and the choice of required receiving system is made by slight tilt of the Cassegrain (secondary) mirror towards the chosen feed. There exists a possibility to work in the prime focus mode, useful essentially only for observing at lower frequencies, say at λ ≥ 50 cm. This possibility requires a removal of the Cassegrain mirror with the help of special maintenance device, which allows also for installation of receiving systems in the prime focus cabin.

One of the most important parameters of a telescope is a reflecting surface accuracy, since it sets limits to highest frequencies at which a telescope can be used. It is well known that if the surface has an rms (root mean square) error of σ, the telescope efficiency is diminished by a factor of

ησ = e–(4πσ/λ)2.

Commonly one assumes that a telescope can be used up to the wavelength λ = 16σ, at which the efficiency drops by 54 % (factor of η_σ = 0.54) relative to the case of a perfect surface^*. The main reflector of the 32 m telescope is estimated to be accurate to 0.4 mm, which means that it should have good efficiency at wavelength of 7 mm and possibly be still usable at 3 mm (about 100 GHz).

II.2  Geometry and Other Characteristics

Geometry of the 32 m radio telescope Main reflector (paraboloid of revolution) Diameter  d  32.0  m Focal length  f  11.2  m f/d  ratio 0.35 Depth of the dish  H = d2/(16f)  5.7143  m Subtended angle  2Θo = 4arctg[d/(4f)] 142.1507  ° Total surface area   8πf2[cos–3(Θo/2)–1]/3  899.45  m2 Aperture (collecting area)  πd2/4 804.25  m2     Equation of the parabola†   r = √{4f(f–z)} = 2f tg(Θ/2)   Cassegrain mode Diameter of the hyperbolic subreflector  ds  3.2  m Height of the secondary focus above the dish vertex  h  1.0  m Angle subtended by the subreflector  2Φo = 2arcctg{2[(f–h)/ds – (f–H)/d]} 18.8256  ° Effective focal length  F = d/[4tg(Φo/2)] 97.1729  m Radio telescope magnification  F/f  8.6762   Foci separation  2c = f–h 10.2  m Eccentricity of the hyperbola  c/a = (F+f)/(F–f) 1.2605   Inclination of the asymptote   α = arccos(a/c) = arccos[(F–f)/(F+f)] 37.5044  ° Distance of the hyperboloid vertex from its foci  c+a 9.1459  m                                     c–a 1.0541  m Prime focus – subreflector edge distance  ρ = ds/(2sinΘo) 1.6914  m Subreflector depth  c–a–(f–H)ds/d 0.5056  m Ray path difference to the foci  (f–h)a/c 8.0917  m Total subreflector surface area   πsinα[(ρ+a)√{ρ(ρ+2a)}–2a2ln √ρ + √{ρ+2a} √{c+a}+√{c–a} ]–π(c2–a2) 8.7728  m2 Aperture blockage by the subreflector   πds2/4  8.0425  m2     Equation of the hyperbola†   r = √{(c2–a2)[(c/a–z/a)2–1]} = (c2–a2)sinΘ /(a+c cosΘ)

†  r is the distance from the symmetry axis of the radio telescope, along which the z coordinate is measured. The z variable origin is at the paraboloid and hyperboloid focus and it is measured towards the dish. Θ is the angle between the z axis and the radius vector.

Unlike in optical astronomy, in radio astronomy the optical geometry does not satisfactorily represent telescope properties of prime import to the user. This is so because of their strong dependence on wavelength or frequency of observations. Such is e.g. the half power beamwidth (or angular resolution) of a radio telescope. This parameter and a few others can be derived from a voltage or power pattern of an antenna.

The voltage pattern is determined by the two-dimensional Fourier transform of electric field distribution over the aperture. If the aperture has circular symmetry this transform reduces to the Hankel transform. In particular, for the aperture in the form of an annulus the normalized voltage pattern can be expressed by the following approximate (an exact solution is derived here) formula:

In this formula for U(x), the components containing J₁ correspond to a uniform field distribution, and those containing J₃(x) — to a distribution weighted by 1 – β(2r/d)².

The antenna power pattern can be written as:

P(θ) = U2(π  d  λ sinθ).

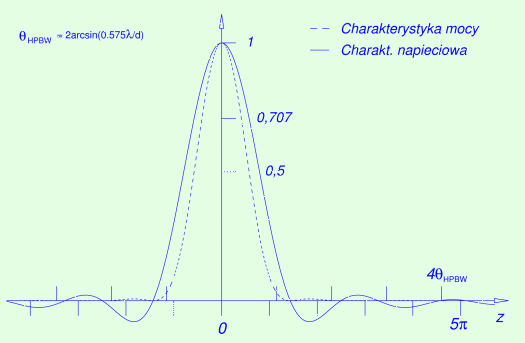
Rys. II.3: Directional pattern for aperture in the form of a ring or annulus with the inner diameter 10 times smaller than the outer one (equal to d), the illumination function diminishing outwardly as 1 – 3(r/d)2. The voltage pattern (continuous curve) is of the form of equation (II.1) with β = 0.75. The broken curve represents the radiation power pattern; it is the square of the voltage pattern. ΘHPBW denotes the width of the main power pattern lobe at its half maximum

The angular resolution, or half power beam width (HPBW), is equal to twice the angle θ = arcsin[xλ/(πd)], at which the power P falls to 50% of its maximum value. For a paraboloid with the diameter d = 32 m numerical calculations give:

ΘHPBW = 2arcsin(1.80706 λ πd )  ≈ 1.15[rad]   λ d   = 1.24' λ [cm]   = 37' [GHz] ν .

The coefficient of 3.614/π = 1.15 is valid for d/d_s = 10 and corresponds to the illumination function 1 – 3(r/d)², i.e. with β = 0.75 which means 10lg(1/β) = 12 dB taper at the dish outer edge. The following table gives angular resolutions of the 32 m telescope at some frequencies commonly used in radio astronomical practice.

Theoretical angular resolution [ΘHPBW = 2arcsin(0.5752λ/d)] for a paraboloidal dish d = 32 m in diameter with a secondary mirror d/10 in diameter. Given is also the directivity D (in the last row). ν [MHz] 327 408 610 1420 1660 2290 5000 11700 22000 30000 100000 λ [cm]  91.7 73.5 49.1 21.1 18.1 13.1 5.996 2.562 1.363 0.999 0.300 ΘHPBW ['] 113 90.8 60.7 26.1 22.3 16.2 7.41 3.17 1.68 1.24 0.371 [°]  1.89 1.51 1.01 0.435 0.372 0.270 0.124 0.053 0.028 0.021 0.006 D/1000  11 17 37 202 276 526 2510 13700 48500 90200 1000000

Define the beam solid angle of a circularly symmetric antenna by:

ΩA= ∫ 4π  Pn(θ,φ) dΩ ≈ 2 π π/2 ∫ 0   P(θ) Pmax sinθ dθ,

where P_n is the normalized power pattern and P_max is the power at the pattern maximum. Then the directivity D can be calculated from:

D =   4π ΩA .

D can be interpreted as an approximate number of discrete sources uniformly distributed over the entire sky given antenna is able to resolve (in practice so interpreted number is roughly an order of magnitude smaller).

The fact that the aperture is finite, i.e. that the radio telescope power pattern is not quite close to the Dirac delta function, means extra losses in its efficiency. The effective aperture A_eff is directly related to the directivity

Aeff =   λ2 4π D.

In the case of the 32 m telescope one finds:

Aeff ≈ 717 m2.

This quantity naturally does not account for the ohmic losses and assumes a perfect shape of the reflecting surface as well as the absence of any shadowing effects. Therefore, in practice the effective area or aperture is determined by observations of radio sources of known flux density, F. If such a source rises the system temperature (see Chapter VII for definitions of various temeperatures) by T_A then

Aeff = 2k TA F  ,

where k is the Boltzmann constant.

II.3  Shadows of the Secondary Mirror and Its Support Struts

Still the aperture blockage remains an important factor because it affects the aperture efficiency. It is estimated that the efficiency decreases by the following factor

ηb =   ( 1 –   blocked area total aperture area ) 2   .

Three components contribute to the blocked area: (1) direct shadow cast by the subreflector, (2) similar shadow of the supporting struts, and (3) shadow of the struts due to blockage of the spherical wave reflected from the dish and converging towards the focal point. The first two components are relatively easily calculable. The third component may pose a difficulty, especially in designs in which the struts do not lie in the plane passing through the dish axis, which is the case with the 32 m telescope that has 8 legs to support the Cassegrain mirror. Both, an original analytical solution to the mentioned problem of skewed struts and a graphical projection lead to about 7.44 % for the loss of aperture area, which converts into about 14 % loss in antenna efficiency due to aperture blockage alone.

Components of the shadow per 1/8 of the aperture

Shadow source	Size [m]	Area [m2]
Subreflector	π×1.62/8	1.0053
Arm — inner part	~0.150×1.10	0.1650
Arm — outer part	0.100×0.42	0.0420
Strut — thinner part (parallel projection)	0.114×1.97	0.2246
Strut — thicker part (parallel projection)	0.159×2.28	0.3625
Strut — type (3) blockage	anal. solution	5.6407
Total shadow area		7.4821
In percent of the aperture  100×8×7.4821/804.25 = 7.44

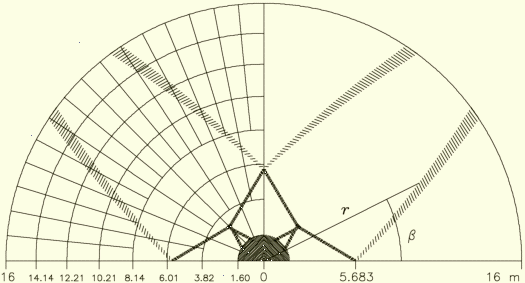
Rys. II.4: Mesh of panels and blocking shadows as projected on the aperture plane of the Torun 32-meter radio telescope. This drawing is to scale. Area shaded lightly (outer shadow) is equal to 22.56 m2, and the black one — 7.62 m2. All curves limiting the outer shadow of a single strut are arcs of a circle. The two longer sides can be expressed as a function of the radial distance r thus: β(r) = βo – arccos[r/(2ro) – 2f2/(rro)], where f is the focal length (11.2 m), and βo and ro equal to 2.3345 rad and 60.987 m for one shadow side and 2.2789 rad and 62.043 m — for the other

II.4  Blind spot near the zenith

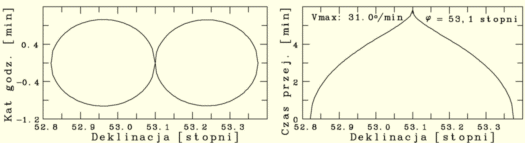
Rys. II.5: Left. Circumzenithal region where the mean azimuthal velocity of cosmic objects is greater then 31°/min at the geographical latitude φ = 53.1°. The axes of this diagram are the declination (in degrees) and hour angle (in minutes of time). Right. The time ('Czas przej.' in minutes) required by the telescope to catch up with the object on the other side of the local meridian. The apparent symmetries with respect to declination equal to φ are only due to the smallness of the differences

The velocity in the azimuth A for a celestial object due to its diurnal rotation is equal to

. A      =   sinφ – sinδ cos z sin2z  = sinφ + cosφ  cosA tg z ,

where φ is the geographical (geodetic) latitude, δ – the declination of the object, and z – its zenith distance (i.e. π/2 minus the elevation or altitude angle). The critical region, wherein a telescope with the maximum tracking speed in the azimuth of V, expressed in natural units of rad/rad or (telescope rotations)/(sky rotations) and defined to be negative for objects transiting between the zenith and the celestial pole (i.e. on the Northern hemisphere for δ > φ), lags behind tracked objects lies between these two declinations:

δ± = φ – arctg  cosφ ±V – sinφ ,

thus constitutes a belt δ_– – δ₊ = ~(2/V)cosφ in width. In particular, for the location of Piwnice (32 m telescope) and V = 120 (i.e. 30°/min) one obtains δ_– – δ₊ = 34.4'.

The hour angle at which a tracked object will start to escape the telescope can be calculated exactly (see e.g. Eq. (9) in this paper) but for practical purposes such a solution is too involved. Instead, this simple expression can be used as a very good approximation:

to ≈   –√ (φ – δ)(δ – δ±) cosδ .

The quantity A_o ≈ –arccos√{(φ – δ) (±V – sinφ)/cosφ} is the corresponding hour angle. Both these angles are assigned negative sign because at this time the object is East of the meridian.