Return to Table of Contents

Chapter VI
Time service — K. Borkowski, J. Usowicz

(Last updated: 2004.09.01)

... At present English version ends here; translation is in progress ...

Jednym z najczulszych punktów prawie wszystkich systemów VLBI są wzorce częstości występujące w roli oscylatorów lokalnych. Ich niestabilność narzuca ograniczenie czasu spójnej integracji funkcji korelacji, a zatem także czułości całego systemu odbiorczego, a dalej — dokładności pomiaru obserwabli. Stabilność, jaką wykazuje współczesny wzorzec wodorowy (nawet poniżej 10^-15), czyni zadość najostrożniejszym ocenom.

Wszystkie atomowe wzorce częstości (albo czasu) opierają się na wykorzystaniu przejść kwantowych między parą poziomów energetycznych atomów lub cząsteczek.

Dla wszystkich użytkowników wzorców częstości najistotniejszą ich charakterystyką jest stabilność. Spośród wielu parametrów opisujących stabilność najczęściej korzysta się z dwupróbkowej statystyki zwanej wariancją Allana i oznaczanej przez s_y²(Dt), która charakteryzuje fluktuacje fazy i częstości sygnału wzorca w dziedzinie czasu na odcinku Dt. Przebieg funkcji s_y typowego wzorca częstości można podzielić na trzy charakterystyczne obszary. Dla małych wartości czasów pomiaru Dt jest to funkcja proporcjonalna do Dt^-1 (biały szum fazowy albo szum migotania), lub Dt^-1/2 (biały szum częstości) zależnie od podstawowych własności szumowych wzorca. Źródłem tych niestabilności może być np. tzw. szum śrutowy we wiązce atomów cezu, fotonowy szum śrutowy w fotokomórce urządzenia rubidowego, czy szum addytywny powstający w odbiorniku mikrofalowym masera wodorowego. Od pewnego (większego) czasu uśredniania niestabilność nie zależy już od Dt, a szumy przypisuje się takim źródłom, jak fluktuacje zasilania i zewnętrznego pola magnetycznego, zmiany zachodzące w elementach składowych wzorca, zmiany natężenia promieniowania mikrofalowego i in. Wreszcie, jest trzecia część funkcji s_y, którą opisuje Dt w potędze od 0 do 1. Jeśli jest to po prostu Dt⁺¹, to fragment ten wyraża czystą zmianę częstości (dryf, np. wskutek starzenia się wzorca), która nie degraduje stabilności wzorca, gdyż można ją dokładnie zmierzyć. Często jednak wykładnik potęgowy nie jest jedynką i sam jest niestabilny, a jego wyznaczenie nie jest łatwe ze względu na wymóg długich czasów uśredniania. Z tego powodu w specyfikacjach konkretnych wzorców ta część charakterystyki stabilności często jest pomijana lub opatrzona uwagą ,,dryf usunięty".

Czas koherentnej integracji sygnału Dt dla interferometrów wielkobazowych w przybliżeniu określa wyrażenie (Klemperer 1972):

w_oDt s_y(Dt) = 1 rad,

gdzie w_o jest częstością kołową oscylatora lokalnego. Wyrażenie to oznacza warunek, by w przeciągu czasu integracji zmiana fazy oscylatora nie przekroczyła radiana. Maksymalna częstość obserwacji (w rad/s) bez znaczącej straty spójności wynosi zatem w przybliżeniu 1/(Dt s_y). Stosując wzorce rubidowe, dla których s_y(10) = 10^-12, i przyjmując czas integracji równy 10 s, znajdujemy ok. 10 GHz na górną granicę częstości obserwacji. Wartość ta jest 100 razy większa dla maserów wodorowych, dla których s_y(10) = 2·10^-14. Użycie wzorca wodorowego w parze (jaką stanowi prosty interferometr) z rubidowym niewiele polepsza czas spójności takiego interferometru w stosunku do przypadku dwóch wzorców rubidowych (Rogers i Moran 1981).

Kartaschoff (1979) pokazał, że odchylenie standartowe czasu mierzonego wzorcem na odcinku Dt wynosi ok. Dt s_y. Przy czasie integracji nieco powyżej 100 s s_y wzorca rubidowego przestaje maleć [utrzymując się na poziomie (2 – 3)·10^-13], co sprawia, że wyrażenie Dt s_y rośnie z upływem czasu powodując wzrost szumu zegara (wzorca). O ile dla czasu koherentnej integracji mniejszego niż 10⁴ s czynnikiem limitującym w eksperymentach z maserami wodorowymi jest atmosfera lub jonosfera, to w przypadku wzorców rubidowych (też cezowych) ograniczenie praktycznie zawsze stanowi sam wzorzec (Rogers i Moran 1981).

VI.1 Wzorzec wodorowy

Maser wodorowy, najlepszy z punktu widzenia potrzeb VLBI, jest urządzeniem aktywnym w takim sensie, że generuje sygnał wprost z przejścia z górnego do dolnego poziomu struktury nadsubtelnej wodoru atomowego w stanie podstawowym. Przy braku pola magnetycznego i w temperaturze zera bezwzględnego, kiedy atomy są nieruchome, przejściu temu odpowiada częstość 1 420 405 751,768 Hz, czyli dobrze znana astronomom emisja fal o długości 21 cm. W celu wydzielenia atomów o odpowiednim stanie energetycznym we wzorcu wodór cząsteczkowy dysocjuje się przez wyładowania elektryczne, a następnie wiązkę otrzymanych atomów przepuszcza przez selektor magnetyczny, w którym następuje przestrzenne rozdzielenie atomów o różnych stanach. Właściwe atomy są teraz kierowane do mikrofalowej komory rezonansowej, gdzie następuje wymuszone uwolnienie energii i wytwarzanie sygnału. Sygnał ten pobiera się za pomocą sondy i używa go do dostrajania fazy oscylatora kwarcowego.

VI.2 Wzorzec rubidowy

W rubidowym wzorcu częstości stabilizuje się 5-megahercowy oscylator kwarcowy względem naturalnego rezonansu atomowego — nadsubtelnego przejścia między dolnym i górnym poziomem rubidu 87 w stanie podstawowym (6 834 685 Hz). Technicznie uzyskuje się to przez optyczne pompowanie atomów ⁸⁷Rb (w celu ich depopulacji) wiązką pochodzącą z takich właśnie atomów, ale dokładnie odfiltrowaną przy pomocy izotopu ⁸⁵Rb. Przejście rezonansowe z powrotem na niższy poziom stymuluje się sygnałem mikrofalowym wytwarzanym przez powielenie do odpowiednio wysokiej częstości sygnału oscylatora lokalnego (kwarcowego). Stopień dostrojenia do rezonansu monitoruje się fotokomórką oświetloną wiązką użytą wcześniej do pompowania. Ponieważ wiązka ta jest absorbowana tym bardziej, im lepsze jest dostrojenie do rezonansu sygnału mikrofalowego, to możliwe staje się użycie sygnału z fotokomórki w pętli sprzężenia zwrotnego do dostrajania częstości drgań oscylatora kwarcowego.

Ustawianie zegara wzorca rubidowego — A. Kępa, W. Szymański

Poniższa instrukcja dotyczy ,,ZEGARA CYFROWEGO - 2" (znajdującego się w pomieszczeniu 47), korzystającego z rubidowego wzorca firmy Hewlett Packard (5065A Rubidium Vapor Frequency Standard).

1. Wstępne nawiązanie do zegara w odbiorniku GPS (zegarek osobisty lub walkie talkie ):

Do USTAWIENIA czasu słonecznego i daty juliańskiej (JD) służą następujące klawisze:

stop — jedyny bistabilny przycisk zatrzymujący wszystkie liczniki

M — minuty czasu

H — godziny czasu

D1 — jednostki i dziesiątki dni juliańskich

D2 — setki (i tysiące) dni juliańskich

D3 — tysiące i dziesiątki tysięcy dni juliańskich

+1^m — inkrementacja licznika minut (rzadko używany)

Ustawianie właściwej liczby tysięcy dni juliańskich należy wykonać klawiszem D3 po ustawieniu setek za pomocą D2. W liczniku JD wyświetlane jest tylko końcowe 5 cyfr po stałych ,,24". Inkrementacja tego licznika następuje w południe (o godz. 12:00).

2. Ponownie sprawdzić sekundy.

3. Ustawić dopełnienie POPRAWKI chodu zegara, wyrażonej w mikrosekundach (ms), do całkowitej liczby sekund (np. dla poprawki równej 1 ms dopełnienie wyniesie 999999):
— na klawiszach ¯D ¯C ¯B ¯A, o wagach 8 4 2 1 (odpowiednio) wpisać kolejne cyfry dopełnienia kodem BCD w taki sposób, że każdą cyfrę ,,wyciska się" na tych klawiszach. Np., aby wprowadzić cyfrę 9 należy pozostawić niewciśnięte klawisze ¯D i ¯A (których wagi sumują się do 9), tj. nadusić klawisze ¯C i ¯B
— po wprowadzeniu cyfry nacisnąć czerwony klawisz P w celu jej wyświetlenia
— cyfry wprowadzać od najstarszej
— po wprowadzeniu wszystkich 6 cyfr (jeśli wypadnie mniej, to z przodu powinny być zera otrzymywane naciśnięciem wszystkich czterech klawiszy) wcisnąć klawisz L (powodujący załadowanie wprowadzonej poprawki do rejestru wewnętrznego), a po nim + lub - powodujące dodanie albo odjęcie poprawki od wskazań zegara
— w przypadku pomyłki przy wprowadzaniu (przed wciśnięciem L) wyświetlacz można ,,wyzerować" (Z) i wprowadzić wszystko od nowa
— sprawdzić, czy wprowadzona poprawka miała właściwy znak i ewentualnie obliczyć następną poprawkę oraz jej dopełnienie i wprowadzić je do zegara.

Na końcu należy sprawdzić, czy po tych wszystkich operacjach wyświetlana jest właściwa sekunda!

4. USTAWIANIE czasu gwiazdowego:
— obliczyć czas gwiazdowy dla jednej z przyszłych pełnych minut
— czerwonym (skrajnym z prawej strony) klawiszem stop zatrzymać zliczanie sekund zegara gwiazdowego aż do chwili, gdy będą zgodne z wybranym czasem
— minuty i godziny ustawić za pomocą klawiszy M i H (odpowiednio).

(Klawisz Z służy do zerowania liczników M i H.)

Miejscowy czas gwiazdowy
Konwencjonalny [Transactions of the International Astronomical Union, XVIII B (1983), 67] średni czas gwiazdowy Greenwich definiuje wyrażenie (w sekundach):

GMST = UT1 + 24110,54841 + 8640184,812866 T + 0,093104 T² - 6,2·10^-6 T³,

gdzie UT1 to czas wyznaczany przez rotację Ziemi (po uwzględnieniu ruchu biegunów), a T = (JD - 2451545)/36525; w okresie 1900.03.01 r. – 2100.02.28 r. kalendarza gregoriańskiego dla daty (dnia) juliańskiej, JD, mamy:

JD = 367R - [(7(R + [(M + 9)/12]))/4] + [275M/9] + D + 1721013,5 + UT1/24^h
gdzie [...] oznacza część całkowitą, R — rok, M — miesiąc, D — dzień miesiąca.
Miejscowy czas jest większy od tego w Greenwich o długość geograficzną miejsca (liczoną dodatnio na wschód od Greenwich), LMST = GMST + l. Dla położenia RT32 z pomiarów VLBI mamy:

l = 18,56405740^° = 1,237603827^h = 1^h14^m15,3738^s

Opuszczając w równaniu na GMST wyrazy wyższego rzędu niż liniowy, w okresie obejmującym lata 1900–2100 wprowadzamy błąd mniejszy niż 0,1^s. Dla praktycznych celów na średni miejscowy czas gwiazdowy możemy więc bezpiecznie przyjmować (w godzinach):

LMST @ 6,6973745583 + l+0,06570982442·(JD-2451545,0) +UT1

@ 7,902124 + 0,06570982442·(JD₁₂ - 2451545,0) + 1,002737909351·UTC

gdzie JD₁₂ to juliańska data w południe danego dnia (tzn. wyrażająca się liczbą całkowitą), zaś UT1 zastąpiliśmy przez czas koordynowany, UTC (różnią się mniej niż o 1^s).
Aby otrzymać czas prawdziwy, należy do średniego dodać aktualną wartość równania równonocy (tj. zrzutowanej na równik niebieski nutacji w długości ekliptycznej, Dycose, co w wartości bezwzględnej jest mniejsze niż 1,2^s). Pamiętać jednak trzeba, że jeśli stosujemy czas prawdziwy, to również współrzędne obiektów muszą być widome (apparent), czyli poprawione na efekt nutacji.

VI.3 Odbiorniki GPS

Global Positioning System

GPS (Global Positioning System) jest satelitarnym systemem rządu Stanów Zjednoczonych przeznaczonym do celów nawigacji, synchronizacji czasu i geodezji. Składa się on z trzech segmentów: kosmicznego (obejmującego 24 satelity, w tym 3 zapasowe), kontrolnego (monitorującego położenia satelitów, synchronizującego ich pracę i przesyłającego poprawki czasu) oraz użytkowników.

Satelity systemu nazywa się NAVSTARami (Navigation System with Time and Ranging). NAVSTARy odbierają sygnały kontrolnego segmentu i wysyłają do użytkowników:

· Dane o poprawności pracy satelity (informacje o jakości wysyłanych sygnałów nawigacyjnych — czy są wiarygodne).

· Efemerydy (szczegółowe dane o orbicie satelity).

· Almanach konstelacji satelitów (przybliżone dane o orbitach wszystkich satelitów).

· Czas.

· Sygnały do pomiaru odległości (ranging signals).

· Dane o poprawkach atmosferycznych.

Każdy NAVSTAR krąży wokół Ziemi po kołowej orbicie na wysokości 20 200 km na jednej z sześciu płaszczyzn nachylonych do równika pod kątem 55°. Okres orbitalny satelitów to 12 godzin. Cała konstelacja zapewnia praktycznie ciągłą jednoczesną widoczność przynajmniej 4 satelitów GPS z każdego miejsca Ziemi.

Segment użytkowników składa się z aparatury, która śledzi satelity NAVSTAR, odbiera ich sygnały i przetwarza je w zależności od konkretnego zastosowania (nawigacja, pomiary pozycyjne). Wspólną, podstawową funkcją wszystkich zastosowań jest wykorzystywanie sygnałów do poprawiania położenia względem powierzchni Ziemi z dokładnością od kilku milimetrów do 100 m, zeleżnie od użytego instrumentarium i warunków jego pracy.

Dla użytkowników cywilnych normalnie dostępne są pomiary w oparciu o tzw. kod C/A przesyłany na częstości L1 (1575,42 MHz), który zapewnia dokładność pozycji w granicach 10 – 30 m (dokładność ta może być celowo degradowana, tzw. tryb SA, o czynnik 1,8 czyli do ~50 m).

Główne źródła błędów wyznaczania położenia to: [1] zamierzona degradacja (30 m), [2] opóźnienie jonosferyczne (20 – 30 m w dzień i 3 – 6 m nocą), [3] opóźnienie troposferyczne (do 30 m), [4] błędy efemeryd (<3 m), oraz [5] błędy rubidowych zegarów satelitarnych (<3 m). Te błędy pozycji transformują się na błędy czasu GPS (30 m to ok. 100 ns).

Odbiornik 1 (GPSTR1): Model 8812 GPS Station Clock

Podstawowe charakterystyki Modelu 8812 firmy TRAK Systems (Tampa, Florida) to:

· Termostatowany wewnętrzny oscylator kwarcowy (B7A) na 10 MHz.

· Wyjścia: 1 PPS (puls na sekundę), ustawialne wyjście wysokiej częstości (do 1 MPPS) i podobne niskiej częstości pulsów (1 – 12 PPH).

· Jeden z czterech (wybieralnych) kodów sygnałów czasu.

· Komputerowy interface RS-232.

· Śledzenie do 6 satelitów.

· Dokładność synchronizacji czasu z UTC/GPS: 0,1 ms (przy celowej degradacji 0,2 – 0,3 ms rms; jeśli żaden satelita nie jest śledzony, to wewnętrzny zegar dryfuje z szybkością 1 ms/godz.)

· Okres nawiązywania do czasu satelitów: typowo ~2 min.

· Dokładność pozycji (długość, szerokość i wysokość): 30 m.

· Nawiązanie do wzorca zewnętrznego: 1 PPS musi być w przedziale ±5 ms od UTC; rozdzielczość pomiarów różnicy wskazań zegarów: 20 ns.

Odbiornik 2 (GPSTR2): CNS Clock

CNS Clock, firmowany jako typ CNSC01-P (P oznacza, że dostarczono go z oprogramowaniem Tac32Plus), pochodzi z CNS Systems Inc. (Communication, Navigation and Surveillance), USA. Głównym podzespołem tego urządzenia, 'zegara', jak się formalnie nazywa, jest odbiornik Motorola Oncore VP. Najważniejsze jego cechy to:

· Dwa niskoimpedancyjne (BNC) wyjścia 1 PPS (puls na sekundę).

· Dwa wyjścia RS232 (1 PPS).

· Bateryjny backup (umożliwia smart start).

· 5V zasilania anteny GPS.

· Dokładność w trybie ustalonej pozycji: < 50 ns (1s, przy włączonym SA).

Do mierzenia różnicy czasów pojawiania się impulsów 1 pps z tego urządzenia i z masera wodorowego służy uniwersalny licznik firmy Hewlett Packard, HP 53131A, z 10-cyfrowym wyświetlaczem. U nas jest on zamontowany w tej samej obudowie, co CNS Clock. Ten system monitorowania chodu masera pracuje od lipca 2001 r.

Rys. VI.1: Porównanie pomiarów za pomocą obu odbiorników, GPSTR1 (odpowiada mu przebieg z dużym rozrzutem) i GPSTR2 (linia biegnąca środkiem `szumów'), w okresie 24 lipca – 16 sierpnia 2001 r.

VI.4 Monitorowanie wzorca wodorowego

Znaczenie dla VLBI

Sprawna korelacja obserwacji VLBI wymaga znajomości zachowania się wzorców wodorowych w poszczególnych stacjach. Praktycznie wszystkie stacje VLBI wyposażone są w odbiorniki sygnałów GPS, które zapewniają stabilną długookresową skalę czasu. Monitorowanie chodu lokalnych zegarów polega zwykle na pomiarze czasu upływającego między lokalnym impulsem sekundowym (sygnał 1 pps) i analogicznym pulsem z odbiornika GPS. Na ogół jest tak, że znak takiego pomiaru jest ujemny jeśli zegar maserowy spóźnia się względem GPS. Dodatkowa droga sygnału z masera po kablach do teleskopu zwiększa tę różnicę (ma to istotne znaczenie, jeśli stacja posiada więcej niż jedną antenę).

Dla wysokich częstości obserwacji tak monitorowany zegar może stanowić dobrą ocenę spodziewanego zapóźnienia (co jest ważne podczas korelacji obserwacji), ale dla bardzo niskich częstości głównym źródłem niestabilności staje się atmosfera Ziemi. Np. na częstości 327 MHz atmosferyczne opóźnienie może sięgać nawet 1 ms. Przy ocenie częstości listków (fringe rates), niedokładne współrzędne stacji i źródeł mogą zdominować predykcje. Ponieważ obecnie korelatory nie interpolują aberracji i parametrów orientacji Ziemi w ciągu doby, podczas analizy obserwacji VLBI obserwuje się skoki o godz. 0 UT rzędu 1,5 ps/s. Można więc spodziewać się tego rzędu rozbieżności podczas procedury poszukiwania listków (fringe search).

Dotychczasowe analizy wskazują, że obecnie w większości obserwacji astronomicznych monitorowanie maserów względem GPS może zapewnić wystarczająco dokładne wartości (epoki i przyśpieszenia) apriori zegara stacyjnego, aby można było zrezygnować z procedury fringe search. Zapóźnienie można przewidzieć przynajmniej z dokładnością 200 ns.

Predykcje przyśpieszenia zegara (clock rate ) z pomiarów GPS jest ograniczone. Jasne jest jednak, że tą drogą można określić rates znacznie dokładniej niż mogą to obecnie sprawdzić korelatory. Wartości 0,5 ps/s są już zauważalne w korelacjach.

Zalecenia co do monitorowania maserów

Ze względu na niedokładność pojedynczych odczytów i potrzebę wielu wyników do oceny rates,

nie zaleca się regularnego przestawiania zegarów

— dobrze określone opóźnienia i przyśpieszenia są lepsze niż wartości bliskie zera. Z tego samego powodu proponuje się nie przeprowadzać konserwacji masera na mniej niż 4 tygodnie przed sesją VLBI.

· Różnicę między pulsem sekundowym GPS i formatera (masera) należy mierzyć i uśredniać przez około 1000 s. Jest to zwykle dostatecznie długo, aby wygładzić lokalne obciążenia (biases ) pomiarów 1 pps.

· Wyeliminować odstające pomiary; chodzi tu o obserwacje GPS zaznaczone (flagged ) przez odbiornik (wartości > 0,5 s).

· Uśrednić wyniki z jednej doby czasu uniwersalnego (UT). Na krótszych odcinkach czasowych stabilność masera powinna być zadowalająca, zaś czas GPS posiada zbyt duże fluktuacje. Uśrednione dane powinny składać się z:
— średniego czasu (MJD) pomiarów (przynajmniej 3 cyfry po kropce)
— średniej różnicy w ms (przynajmniej 2 cyfry po kropce)
— średniokwadratowego (rms) błędu pomiarów różnicy (2 cyfry po kropce).

· Wyeliminować błędne średnie dzienne (rms > 200 ns)

Zegar powinien być monitorowany w sposób ciągły. Pomiary winny być sprawdzane przynajmniej raz na miesiąc (ręcznie) i odpowiedni plik wyedytowany w celu wpisania komentarzy o znanych lokalnych zmianach. Jako minimalne wymaganie należy przyjąć, że monitoring prowadzi się przynajmniej na 1 tydzień przed sesją, podczas sesji i 1 dzień po sesji.

Gromadzenie i opracowanie danych

Odczyty różnicy czasu impulsu sekundowego zegara GPS i masera wodorowego są zapisywane do dziennika (specjalny zeszyt) przez obserwatorów z częstością ok. jeden raz na godzinę. Dane te następnie są przepisywane do pliku gps-h.dat zawierającego wszystkie dotychczasowe pomiary w formie yy mm dd hhmm wartość, gdzie datę (rok, miesiąc i dzień) można pominąć, jeśli wystąpiła już wcześniej w pliku. W pliku tym mogą ponadto występować komentarze (wiersze rozpoczynające się od znaku #) i opisy zmiany ciągłości (wiersze ze znakiem &).

Do opracowania tych danych z wzorca GPSTR1 służy program gps-h, który generuje m.in. pliki miesięczne gotowe do złożenia na komputerze w Bologni. Zarówno ten program, jak i plik danych znajdują się w komputerze EUKA (pok. 31) w katalogu e:\VLBI\gps.

Dane z odbiornika GPSTR2 są od lipca 2001 r. gromadzone automatycznie na komputerze FS w katalogu /usr3/gpsdata w formie plików ASCII, jeden plik na dzień, o nazwach Tyyyyddd.TR, w których zakodowany jest rok i dzień roku (np. T2003033.TR — plik z 2 lutego 2003 roku). Pliki te zawierają wiersze (najczęściej w liczbie 90, czyli co 16 minut) odpowiadające pojedynczym wyznaczeniom. Tak wyglądają pierwsze 3 wiersze w pliku T2003033.TR:

52672.00555556 5.524644 0.032195 GPSTR2 # 960 0
52672.01667246 5.528502 0.031576 GPSTR2 # 960 0
52672.02778357 5.530518 0.031932 GPSTR2 # 960 0

W pierwszej kolumnie widzimy tutaj moment wyznaczenia (MJD), a kolejne dane to: różnica wskazań zegara lokalnego i czasu GPS (ms), średnikwadratowy błąd tego pomiaru (ms), lokalna nazwa odbiornika GPS (tu GPSTR2) oraz (po znaku #) liczby pomiarów wziętych do wyznaczenia i odrzuconych. Do sporządzania raportu miesięcznego z takich danych służy program MonthRep znajdujący się w katalogu e:\VLBI\gps\GPS2 w komputerze EUKA (pok. 31).

Format i rozpowszechnianie wyników

Plik z danymi o stabilności masera uzyskanymi z pomiarów względem zegara GPS ma mieć nazwę gps.tr, w której człon tr jest standartowym kodem toruńskiej stacji VLBI. Plik ten, redagowany w ASCII, może zawierać trzy typy linii (wierszy), np.:

# wiersz samego komentarza zaczyna sie od znaku #
& specjalny komentarz wskazujacy miejsca nieciaglosci zaczyna sie od &
50389.581 0.435 0.087 GPSTR1 komentarz do tego wyniku — wiersz danych

W wierszu danych pierwsze cztery kolumny (oddzielone odstępem) zawierają (1) zmodyfikowaną datę juliańską (MJD = JD - 2400000,5) pomiaru, (2) wynik pomiaru w ms (w naszym przypadku ta wartość musi być opatrzona przeciwnym znakiem niż ten z bezpośrednich pomiarów w celu dostosowania do konwencji przyjętej na korelatorach VLBI), (3) błąd tego pomiaru w ms, oraz (4) nazwę i numer odbiornika GPS (nazwa ta zawiera człon będący kodem stacji, u nas TR, oraz kolejny numer odbiornika GPS w stacji, u nas 1 lub 2). Po czwartej kolumnie można zamieszczać komentarze.

Pliki należy składać przynajmniej raz w miesiącu (w czasie sesji VLBI zaraz po każdym testowym eksperymencie) na komputerze VAX w Bologni do podkatalogu /data/vlb_arc/home/gps/mmmyy , gdzie mmmyy oznacza miesiąc i rok (np.feb03):

ftp vlbeer.ira.cnr.it

user: evn

password: *********** (tu podać niejawne hasło)

cd gps/feb03

put FEB03GPS.TR gps.tr (FEB03GPS.TR to lokalna nazwa pliku)

bye

Fragment pliku gps-h.dat Plik gps/apr97/gps.tr na vlbeer.ira.cnr.it

97 5 6 704 10.78 # Apr97 [05/02/97] &7:20 UT -new synth. freq. 5751.6631 # Data based on irregular number 725 10.8 # of readings (N) made manually 750 10.82 # MJD offset rms GPSname N 836 10.76 50539.456 -5.907 0.037 GPSTR1 6 920 10.66 50540.547 -6.017 0.059 GPSTR1 12 1021 10.8 50541.626 -6.152 0.086 GPSTR1 12 1125 10.88 50542.369 -6.191 0.100 GPSTR1 9 1225 10.82 50543.874 -6.423 0.039 GPSTR1 6 1317 10.7 50544.068 -6.407 0.031 GPSTR1 3 1404 10.7 50545.525 -6.630 0.080 GPSTR1 10 1410 10.74 50546.503 -6.729 0.115 GPSTR1 11 1548 10.68 50547.652 -6.860 0.069 GPSTR1 15 97 5 7 707 10.66 50548.480 -6.929 0.117 GPSTR1 14 946 10.84 50549.441 -7.042 0.103 GPSTR1 9 1128 10.54 50550.568 -7.312 0.072 GPSTR1 5 1256 10.54 50552.503 -7.500 0.049 GPSTR1 6 1412 10.7 50553.490 -7.617 0.117 GPSTR1 8 1546 10.5 50554.556 -7.692 0.085 GPSTR1 10 97 5 8 515 10.52 50555.632 -7.871 0.076 GPSTR1 18 625 10.3 50556.593 -8.022 0.110 GPSTR1 18 747 10.46 50557.305 -8.080 0.101 GPSTR1 7 819 10.44 50558.681 -8.320 0.000 GPSTR1 1 1140 10.4 50559.402 -8.440 0.108 GPSTR1 4 1234 10.5 50560.453 -8.526 0.098 GPSTR1 10 1327 10.38 50561.554 -8.702 0.086 GPSTR1 11 97 5 9 702 10.36 50562.446 -8.817 0.136 GPSTR1 7 732 10.3 50563.442 -8.956 0.084 GPSTR1 9 817 10.38 50564.557 -9.150 0.104 GPSTR1 4 905 10.4 50566.478 -9.394 0.056 GPSTR1 7 1010 10.24 50567.426 -9.485 0.098 GPSTR1 8 1108 10.3 50568.500 -9.680 0.097 GPSTR1 6 1154 10.26 1330 10.14 1404 10.3 1533 10.2 97 5 10 907 10.12 926 10.04 1005 10.1 1042 10.12 97 5 11 1033 9.86 1200 9.88 1308 10

Korekcja częstości wzorca

Zakładając, że częstość podstawowa wzorca zmienia się liniowo z czasem standartowym T (UT, GPS lub innym), n(T) = n + pT, wskazanie opartego na nim zegara opisuje wyrażenie:

t(T) =

T
ó
ő
T_°

n(T˘)

n_o

dT˘ = a +

n_o

T +

2n_o

T²,

gdzie n_o jest nominalną częstością wzorca (dla masera H n_o = 1420 405 751 Hz), zaś a jest pewną stałą. Odchyłkę chodu tego zegara od czasu standartowego można więc przedstawić w postaci wzoru

y = t(T) - T = a + (

n_o

- 1)T +

2n_o

T².

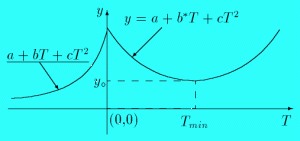
Liniowy dryf częstości wzorca prowadzi zatem do parabolicznego przebiegu odchyłki wskazań takiego zegara: y = a + bT + cT². Jeśli do pomiarów y_i (w ms) dopasujemy parametry a [ms], b [ms/d] i c [ms/d²], to można będzie stąd wyznaczyć rzeczywistą częstość n w chwili T = 0 oraz prędkość jej zmiany:

n
n_o

=

(1 + b·10^-6/86400)

p
n_o

=

2c·10^-6/86400² [1/d],

gdzie współczynniki liczbowe zmieniają wymiar b i c z ms/d i ms/d² na s/s i s/(sd) = d^-1, odpowiednio (86400 to ilość sekund w dobie), a wyniki otrzymuje się w podanych jednostkach, jeśli n_o zostanie wyrażone w Hz.

$RysVI-TeX.gif$
Aby odchyłkę y utrzymać w ,,przyzwoitym" zakresie (np.0 ¸ 10 ms), co pewien okres czasu trzeba korygować częstość wzorcową. Rozsądne jest takie przestrojenie, które zapewni najdłuższy odstęp czasu między kolejnymi korekcjami. Jeśli zegar systematycznie śpieszy (tak jest w naszym przypadku), optymalną poprawkę można obliczyć przyjmując, że nowa wartość b^* powinna zapewnić zmniejszenie się odchyłki y od wskazania bieżącego do pewnej minimalnej wartości y_o (nie powinna być mniejsza od -10 ms). Będzie to zatem minimum funkcji y(T) i przypadnie dla T = T_min spełniającego równość y˘(T_min) = 0, czyli b^* + 2cT_min = 0, albo T_min = -b^*/(2c). Nowa wartość b^* spełnia również równanie a + b^*T_min + cT_min² = y_o, skąd:

b^* = -
Ö

(a - y_o)4c

.

Częstość wzorca należy więc zmniejszyć o wartość odpowiadającą różnicy b i b^*, czyli o

dn = n_o [b + 2
Ö

(a - y_o)c

]·10^-6/86400,

gdzie a oraz y_o wyrażone są w ms, b w ms/d, c w ms/d², a dn dostaje się z tego wzoru w takich samych jednostkach jak n_o (np. Hz).

Rys. VI.2: Wyniki (w ms) pomiarów chodu wzorca EFOS-15 względem czasu GPS w okresie 3 maj 1995 r. — 31 sierpień 2001 r. Wszystkie te wyniki uzyskano przy użyciu odbiornika GPSTR1.

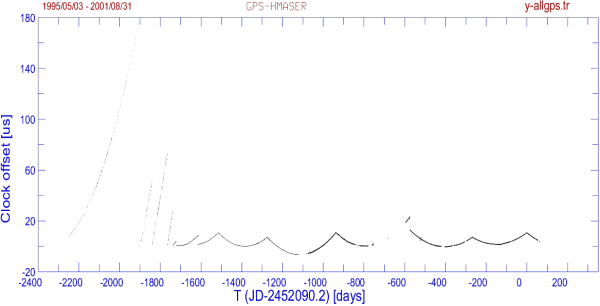Wyniki dopasowania parabol do pomiarów chodu masera H

Oprócz zakresu słuszności (okres między przestrojeniami wzorca) i współczynników funkcji parabolicznej w tabeli podano oszacowanie dokładności całego dopasowania (s = sigma), błąd parametru c (sigma(c)) oraz wielkość dn = df (dla y_o = 0) i ilość danych wziętych do dopasowania (N).

No MJD1 MJD2 a b c sigma sigma(c) df[Hz] N 1 49841.38 50184.47 176.915 0.8159 0.000945 0.2623 0.000002 0.02686 205 2 50184.47 50189.32 4.050 0.8085 0.002865 0.0014 0.000387 0.01683 4 3 50190.36 50248.34 50.010 0.9027 0.000759 0.0631 0.000043 0.02125 31 4 50249.52 50324.36 73.307 1.0272 0.000831 0.0635 0.000018 0.02500 64 5 50324.66 50349.47 26.236 1.0512 0.000522 0.0785 0.000335 0.02113 23 6 50349.73 50350.33 0.000 0.0000 0.000000 0.0000 0.000000 0.00000 2 7 50350.51 50351.30 0.000 0.0000 0.000000 0.0000 0.000000 0.00000 2 8 50351.52 50367.47 3.757 0.1889 0.000807 0.0337 0.000386 0.00491 17 9 50367.63 50374.39 0.407-0.0938-0.005263 0.0212 0.001817 -0.00154 7 10 50374.66 50475.42 8.666 0.1735 0.000908 0.0667 0.000009 0.00577 97 11 50475.52 50574.29 10.608 0.1587 0.000678 0.0389 0.000005 0.00540 94 12 50574.47 50813.80 7.148 0.1325 0.000615 0.0733 0.000001 0.00436 215 13 50814.09 51151.27 10.703 0.1937 0.000544 0.1033 0.000001 0.00569 293 14 51151.78 51514.30 22.889 0.2101 0.000486 0.2001 0.000001 0.00692 172 15 51514.80 51821.23 7.207 0.1140 0.000431 0.1202 0.000001 0.00371 279 16 51821.74 52089.21 10.784 0.1215 0.000403 0.1234 0.000001 0.00417 265 17 52089.73 52152.50 3.686-0.1022 0.000125 0.0832 0.000037 -0.00097 59

Do praktycznych obliczeń zgodnych z powyższymi rozważaniami służy program plot-ps2 lub jego starsza wersja plot-gps (oba znajdują się w katalogu e:\VLBI\gps\plots na komputerze EUKA) analizujący dane pomiarowe (przygotowane programem gps-h). Załączona tabelka stanowi wynik obliczeń wykonanych tym programem. Obejmuje ona pomiary wzorca wodorowego od początku maja 1995 r. do końca sierpnia 2001 r. Warto zauważyć, że instrukcja producenta informuje, że EFOS-15 może wykazywać dryfy częstotliwości rzędu 1 – 2·10^-14 na dobę czyli 0,00086 – 0,00170 ms/d², tj. w jednostkach parametru c.

Rys. VI.3: Wyniki (w ms) pomiarów chodu wzorca EFOS-15 w okresie od 26 stycznia do 26 maja 1997 r. Najlepiej dopasowana parabola do pierwszych 949 pomiarów (do 6 maja) ma postać: 10,592 + 0,1580·T + 0,00067·T², gdzie T liczone jest w dobach od 6 maja, a wartości numeryczne wyrażają mikrosekundy.

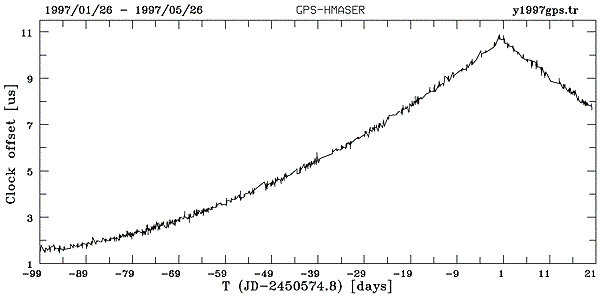
Korekcji należy dokonać przez zmniejszenie aktualnej częstości syntezera maserowego (której nominalna wartość wynosi 5751,68930 Hz) o obliczoną wartość dn. Wprowadzanie poprawek częstości umożliwia program MONIT7 na laptopie (Epson L2) wzorca. Należy mianowicie wybrać opcję F i zmodyfikować syntezowaną częstość korzystając z klawiszy numerycznych oraz ¬ i ®. Przykładowo, w dniu 6 maja 1997 r. przestrojono wzorzec przez zmianę częstości syntezera o 0,0051 Hz, z dotychczasowej wartości 5751,66820 na 5751,66310 Hz. Poprawkę 0,0051 uzyskano z wyznaczenia a, b i c w okresie 26-01-97 – 2-05-97 oraz przyjęcia y_o = 0,75 ms. Takiemu przestrojeniu odpowiada nowe b (czyli b^*) ok. -0,16 ms/d, oznaczające, że najbliższe minimum przypadnie za -b^*/(2c) » 90¸120 dni (przy założeniu, że utrzyma się warunek 0,00065 < c < 0,00090).

W przypadku niestabilnego chodu wzorca (po 2001 r. takie niestabilności obserwujemy coraz częściej) może nie udać się dopasować sensownej paraboli do wyników pomiarów. W razie dużych szybkości zmian w pomiarach należy wtedy ocenić tylko liniowy składnik zmian (b, wg naszych oznaczeń, w ms/d) i obliczyć wartość poprawki częstości wzorca (w hercach), niwelującej ten dryf, ze wzoru:

dn = b·1420 405 751·10^-6/86400 = 0,016440 b @ b/61 [Hz].

File first posted on 1 September 2004.

Chapter VITime service — K. Borkowski, J. Usowicz