Uzupełnienia
(Ostatnia aktualizacja: 2003.08.12)
XII.1 Przeliczanie współrzędnych
Wzory trygonometrii sferycznej
Najkrótsza droga między dwoma punktami na sferze wiedzie wzdłuż
wielkiego koła (albo okręgu ), tzn. koła którego
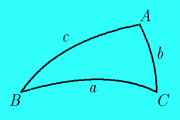
płaszczyzna przechodzi przez środek sfery. Trójkąt sferyczny
powstaje z połączenia łukami kół wielkich (tworzącymi boki
trójkąta) najkrótszymi drogami trzech punktów na sferze nazywanych
wierzchołkami trójkąta. Długości boków wyraża się kątami
między odpowiednimi prostymi poprowadzonymi ze środka sfery przez
wspomniane punkty. Wierzchołkowe kąty A, B oraz C są kątami zawartymi
między płaszczyznami kół wielkich odpowiadających bokom b i c,
a i c oraz a i b, odpowiednio. Zarówno boki jak i kąty wierzchołkowe w
trójkątach sferycznych są (z definicji) mniejsze od 180°.
Wzory Gaussa
sin a
sin A |
= |
sin b
sin B
| = |
sin c
sin C
|
| — twierdzenie sinusów |
|
cos a = cos b cos c + sin b sin c cos A | — twierdzenie kosinusów |
|
sin a cos B = cos b sin c –
sin b cos c cos A | — wzór mieszany |
Inne wzory
|
cos A = | –cos B cos C
+ sin B sin C cos a |
|
sin A cos b = | cos B sin C + sin B cos C cos a |
|
Pole trójkąta sferycznego wynosi
gdzie R jest promieniem sfery a
ε = A + B + C –
π, tzw. nadmiar albo przewyżka
sferyczna, musi być wyrażone w radianach. Nadmiar sferyczny można
też obliczyć ze wzoru:
Przekształcenia układów topocentrycznych, geocentrycznych i
heliocentrycznych
Transformację współrzędnych między układami topocentrycznym,
geocentrycznym i heliocentrycznym przeprowadzamy zwykle na
współrzędnych prostokątnych. Jeśli robimy takie przekształcenie,
to automatycznie uwzględniana jest paralaksa związana z
danymi układami.
Współrzędnymi prostokątnymi w drugim układzie są współrzędne
w pierwszym pomniejszone o współrzędne początku pierwszego układu
w drugim (dotyczy to oczywiście dwóch układów tego samego rodzaju,
np. równikowych heliocentrycznych i równikowych geocentrycznych).
Transformacja współrzędnych pomiędzy dwoma układami o wspólnym
początku może polegać na rozwiązaniu odpowiedniego trójkąta
sferycznego. Rozwiązanie uzyskuje się przez zastosowanie wzorów Gaussa.
Prostokątne ↔ biegunowe
Związki między współrzędnymi prostokątnymi (X,Y,Z) i biegunowymi
(R,φ,θ)
zapisuje się następująco:
przy czym prawo- lub lewoskrętność układu wyraża się kierunkiem pomiaru
współrzędnej Y i θ, gdy patrzymy ze środka (początku)
układu w kierunku osi –X mając oś Z skierowaną do góry (układy
prawoskrętne podlegają regule prawej dłoni albo śruby prawoskrętnej).
Geodezyjne ↔ geocentryczne
Współrzędne geodezyjne można przeliczyć na geocentryczne następująco:
gdzie a i b są dużą i małą półosią elipsoidy, H jest
wysokością ponad jej powierzchnię (dodatnio w górę) zaś
(szerokość zredukowana). Oczywiście, szerokość geocentryczna
a długość (geograficzna) jest ta sama w obu układach.
Transformacja odwrotna nastręcza
pewne
trudności. Opracowano szereg algorytmów iteracyjnych.
Oto jeden z najbardziej efektywnych (Bowring 1976). Najpierw oblicza
się ,,zerowe" przybliżenie szerokości zredukowanej:
a pierwsze przybliżenie na ψ dostaje się z:
|
tanψ = |
bZ + (a2 –
b2)sin3ψo
ar – (a2 –
b2)cos3ψo
|
. |
|
Drugie i zarazem ostatnie przybliżenie jest powtórzeniem pierwszego po
podstawieniu ψ w miejsce
ψo.
Szerokość geodezyjna jest teraz równa:
zaś wysokość nad elipsoidą można obliczyć na kilka sposobów,
np. ze wzoru
|
H = |
( |
r – a |
√
|
1 + tan2ψ
|
) |
cosφ + Z sinφ. |
|
Ta procedura w praktyce daje dokładności pojedynczych nanometrów
(10–9 m,
co jest na granicy podwójnej precyzji większości
współczesnych obliczeń komputerowych) w zakresie wysokości
–5000 ÷ +1 000 000 km i dla wszystkich szerokości
(wyłączając oczywiście punkty bardzo bliskie bieguna).
W tym względzie nie ustępuje ona algorytmom opartym o
rozwiązania
ścisłe.
Na powierzchni elipsoidy (dla H = 0 m) mamy prosty i ścisły związek
szerokości geodezyjnej z geocentryczną:
|
φ'
= arctan | ( |
b2
a2
|
tanφ | ) |
lub
φ = arctan |
( |
a2
b2 |
tanφ' |
) |
. |
|
Horyzontalne ↔ równikowe
Transformacja współrzędnych sferycznych polega na rozwiązaniu
trójkąta sferycznego, którego wierzchołkami są bieguny,
tj. miejsca przebicia sfery przez osie główne układów (po północnej
stronie nieba), i dowolny punkt na sferze.
W przypadku układów horyzontalnego i równikowego należy rozwiązać
trójkąt nazywany paralaktycznym. Jego boki mają wartości:
90° – φ (odległość biegunów;
φ jest szerokością geograficzną miejsca
obserwacji), 90° – h = z
(odległość zenitalna) i 90° – δ
(dopełnienie deklinacji do 90°). Dwa z kątów wierzchołkowych mają
wartości t (przy biegunie niebieskim) i 180° – a (przy zenicie).
Oto rozwiązanie tego trójkąta (polegające na zastosowaniu wzorów
Gaussa) pozwalające przeliczyć współrzędne horyzontalne na
równikowe:
|
|
|
|
sin h sinφ – cos h cosφ
cos a |
| |
|
|
|
|
| |
|
sin h cosφ + cos h sinφ
cos a. | | (XII.1) |
Dwa ostatnie równania można zapisać prościej pamiętając
jednak o znakach licznika (znak sinusa obliczanego kąta t) i
mianownika (znak kosinusa tego kąta), które pozwalają określić
ćwiartkę kąta pełnego rozwiązania na kąt godzinny, t:
|
tan t = | sin a
tan h cosφ
+ sinφ cos a |
. |
|
Wzory typu tan t = x/y są szczególnie efektywne w zastosowaniach
na kalkulatory posiadających wbudowaną funkcję
R→P (też: TO POLAR,
→P) służącą
do transformacji współrzędnych prostokątnych: x (nasz licznik
prawej strony wzoru) i y (nasz mianownik) na biegunowe:
Θ
(nasze t) i r, albo funkcji ATAN2(x,y), która
występuje w niektórych językach programowania (np.FORTRAN lub C).
Przekształcenie odwrotne, do zamiany współrzędnych równikowych
na horyzontalne (por.
praktyczny program
w Fortranie), otrzymuje się podobnie (poprzez wzory Gaussa):
| |
|
sinδ
sinφ + cosδ
cosφ
cos t |
| |
| |
|
|
|
|
–sinδ
cosφ + cosδ
sinφ cos t |
|
|
| (XII.2) |
z analogicznym skróconym zapisem:
|
tan a = |
sin t
–tanδ
cosφ + sinφ
cos t
| . |
|
Równikowe ↔ ekliptyczne
W celu przekształcenia współrzędnych równikowych na ekliptyczne
lub odwrotnie wykorzystujemy trójkąt o wierzchołkach w biegunie niebieskim,
biegunie ekliptyki i wybranym miejscu. Trójkąt ten ma boki ε
(między biegunami; jest to jednocześnie kąt nachylenia równika do
ekliptyki — tak, jak w trójkącie paralaktycznym 90° – φ jest
nachyleniem płaszczyzny horyzontu do równika),
90° – β i 90° – δ,
a kąty przy biegunach wynoszą 90° – λ
(naprzeciw boku 90° – δ) i
90° + α (naprzeciw boku 90° – β).
Oto skrócony zapis ścisłych transformacji współrzędnych tych układów w obie strony
(por. praktyczny program w Fortranie):
|
sinδ = |
sinε cosβ
sinλ + cosε
sinβ |
|
|
tanα = |
cosε sinλ
– sinε
tanβ
cosλ |
|
|
|
sinβ = |
cosε sinδ
– sinε
cosδ sinα |
|
|
tanλ = |
cosε sinα
+ sinε tanδ
cosα |
|
|
| (XII.3) |
Równikowe ↔ galaktyczne
Nowe współrzędne galaktyczne (lII,bII) z równikowymi
na epokę (sic!) B1950 wiążą następujące równania (por.
praktyczny program w Fortranie):
|
|
|
|
sinδ cos62,6° –
cosδ sin(α
– 282,25°) sin62,6° | |
|
|
|
|
|
cosδ sin(α
– 282,25°) cos62,6°
+ sinδ sin62,6°
cosδ cos(α
– 282,25°) |
|
| |
|
|
|
|
cos bII sin(lII – 33°)
sin62,6° + sin bII cos62,6° |
|
|
|
|
|
sin(lII – 33°)
cos62,6° – tan bII sin62,6°
cos(lII – 33°) |
.
|
| |
| (XII.4) |
XII.2 Efemerydy planet
Współrzędne równikowe, horyzontalne i ekliptyczne, zarówno geocentryczne,
jak i topocentryczne, astrometryczne i widome wszystkich planet, Słońca i
Księżyca pozwala obliczać przygotowany w 2002 r. program PlanJPL.
Program ten korzysta z najnowszych (wygenerowanych w Ameryce w
1997 r.) numerycznych efemeryd JPL obejmujących lata 1600–2201:
Planetary
and Lunar Ephemerides DE405/LE405. Efemerydy DE405 są odniesione do
ICRF (International Celestial Reference Frame). Układ odniesienia
starszych efemeryd JPL, które w latach 1984–2002 były podstawą obliczania
położeń publikowanych w The Astronomical Almanac (zob.
wersję Online), tj. DE200/LE200,
nie różni się od ICRF więcej niż o 0,01".
W wersji zainstalowanej na komputerze FS program PlanJPL
uruchamia się poleceniem:
którego niezbyt adekwatna nazwa (Moon + RT) pozostała po
pierwotnym programie przeznaczonym do wyliczania przybliżonych
współrzędnych Księżyca dla geograficznego położenia RT32.
Obecnie to samo polecenie
powoduje wywołanie programu PlanJPL, który przy starcie
skonfigurowany jest także na wyświetlanie aktualnych
topocentrycznych współrzędnych Księżyca wyliczonych dla
radioteleskopu w Piwnicach, ale użytkownik łatwo może wybrać
Słońce (opcja b0) lub dowolną z planet, a także zmienić
układ współrzędnych oraz rodzaj wyświetlanych dodatkowych danych
astronomicznych (zamiast średnicy tarczy można wywołać
odległość ciała lub jego optyczną jasność, zamiast temperatury
jasnościowej (Tb) można wyświetlić kąt fazowy, fazę lub
elongację, zaś zamiast miejscowego czasu gwiazdowego — czas
Greenwich (opcja t1).
Wiele z opcji programu przeznaczonych jest do szczególnych
zastosowań (np. uwzględnianie refrakcji przy obliczaniu
położenia) lub do porównywania z wynikami innych programów
albo publikacji. Np. współrzędne geocentryczne uzyskamy
usuwając poprawkę na paralaksę (tzn. wpisując opcję c0),
współrzędne geometryczne (zamiast astrometrycznych) —
usuwając poprawkę na aberrację (a0), odniesienie do epoki
J2000 — eliminując precesję (p0) i nutację (n0),
współrzędne w czasie dynamicznym (TDT), tj. tak jak w rocznikach
astronomicznych — zerując parametr ΔT
= deltaT = ET – UT (e0).
Program wylicza także przybliżoną temperaturę jasnościową
Tb wybranego ciała na częstości 12 GHz (tę częstość można
zmienić opcją f, np. 'f3 30' przestawi ją na
30 GHz) przez liniową interpolację danych na częstościach:
1, 1.6, 5, 10, 30 i 100 GHz. Wielkość ta może być użyteczna do
celow kalibracyjnych. Trzeba jednak pamiętać, że dane, które
użyto w programie, pochodzą na ogół z lat 60-tych, więc mogą
być obarczone sporymi błędami. Zostały one zakodowane w
następującym podprogramie:
double precision function Tbr(f,iBody)
c Estimates the brightness temperature of planets at frequency f [GHz]
implicit real*8 (a-h,o-z)
dimension T(6,0:10),fi(6)
data ! fi is frequency in GHz
*fi/1d0, 1.6d0, 5d0, 10d0, 30d0, 100d0/, ! Surface Temp
*T/1.2d5,7.5d4,2.2d4, 12d3, 8.2d3, 7.3d3, ! Sun
* 0420,0397, 385, 03*380d0, ! Merc 100-700
* 600, 600, 600, 575, 420, 350, ! Ven 730
* 257.8,249.0,239.4, 234.1,230.5,230, ! Moon - Kuzmin+,1964
c for Moon given is mean temp. of the disk center; actual values may
c differ by about +/-1 (1GHz) to +/-50 K (100GHz) depending on optical
c phase
* 0230, 227, 190, 0187, 0185, 0183, ! Mars 183-268
* 5500,2100, 600, 175, 145, 130, ! Jup 124
* 0270, 255, 160, 106, 0100, 095, ! Sat 95
* 0210, 197, 180, 0160, 0100, 080, ! Uran 58
* 2*0140, 130, 0110, 090, 070, ! Nept 59
* 02*130, 0120, 0100, 080, 060, ! Pluto 50
* 6*0d0/ ! E-M baryc
do 1 i=2,6
if(f.le.fi(i)) go to 2
1 continue
i=i-1
2 Tbr=T(i-1,ibody)
Tbr=Tbr+(T(i,ibody)-Tbr)*(f-fi(i-1))/(fi(i)-fi(i-1))
end
|
Ponadto Tb Księżyca i Wenus
silnie zależy od ich fazy. Dla Księżyca program liczy pewną
średnią temperaturę centralnej części dysku, zaś w przypadku
Wenus są to wartości nieoświetlonej części tarczy (dla fazy
bliskiej zera). Istnieje też opcja (s3) wyświetlania
spodziewanej temperatury antenowej idealnego (100-procentowa
skuteczność wykorzystania powierzchni zbierającej) RT32
skierowanego na ciało, która może posłużyć jedynie do
zorientowania się, które z ciał nadaje się do kalibracji
(po s3 i b11 otrzymamy listę parametrów dla
wszystkich 10-ciu ciał Układu Słonecznego).
Plik źródłowy programu (o nazwie PlanJPL.for napisany
w języku Fortran), wykonawczy (moon) oraz dane JPL (plik
JPL405) znajdują się w katalogu /users/kb/moon (na FS).
Do kompilacji użyto linuxowego kompilatora g77. Plik JPL405
zawiera binarne dane na lata 2000 – 2019 (włącznie), ale
w razie potrzeby można go zamienić na inny. Wymiana wymaga
skompilowania danych z formatu ASCII dostępnych pod internetowym adresem
FTP:
ssd.jpl.nasa.gov w katalogu
pub/ephem/export/ascii
(uwaga: mimo, że są to dane ASCII koniecznie trzeba ściągać je jako
binarne!). Do tej kompilacji służą gotowe programy fortranowskie
umieszczone w innym katalogu na tym samym serwerze FTP.
Poprawność obliczeń programu testowano przez kilka miesięcy
2002 r. porównując je głównie z danymi The Astronomical Almanac
(dane geocentryczne na 0 godz. czasu dynamicznego, TDT lub ET)
oraz z programu opracowanego w Observatoire de Paris, Planeph,
v. 4.2, który liczy efemerydy analitycznie w oparciu o DE403.
Francuski program pozwolił na porównania w innych układach
odniesienia, w szczególności w topocentrycznym. Uzyskiwano zgodność
na poziomie kilku setnych części sekundy łuku dla
położeń geocentrycznych i czasu dynamicznego; dla UT i położeń
topocentrycznych sytuacja jest o około rząd wielkości gorsza,
co można spisać na karb różnic w algorytmach oraz błędów predykcji
różnicy TDT – UT (program Planeph
powstał w 1997 r.).
Poniżej zamieszczamy przykład wywołania i obsługi omawianego programu
(wzięty z okna telnet-u), w którym pokazano m.in. wszystkie
opcje programu (po wpisaniu parametru o). Operacje
użytkownika są tutaj wyróżnione kolorem
(symbol ż oznacza zmianę
wiersza i powrót karetki czyli klawisz ENTER).
$ moonrt ż
Lunar, solar & planetary topocentric data for location of TRAO - RT32
(coordinates [+/-1"] & diameter in degrees, phase [0(new)-1.0(full)])
[On prompt: ENTER = Refresh, q/o/? = Quit/Options/Info]
2003.01.29, Wed, 29 DoY, JD(noon)=2452669 J2003.077 Ephemeris of Moon
UT1 RA Dec Azimuth Altit Diameter Tb[K] LocalAppST
9:16:09 270.9554 -26.4574 13.4563 9.4016 0.529994 234 19:03:15.4
9:17:00 270.9621 -26.4577 13.6412 9.3722 0.529988 234 19:04:06.5 >b6 ż
2003Jan29 82.0837 22.0356 202.6226 -12.0468 0.005223 105 Saturn >o ż
Options at prompt: H/i - Head/current state (param's)
p0/1 - precession*0/1 n0/1 - nutation*0/1
a0/1 - aberration*0/1 r0/1 - refraction*0/1
c0/1 - parallax*0/1 (geoc./topoc.) t0/1 - local/Greenwich sidereal time
z0/1 - ecliptic/horizon coord. --> z1/2 - azimuth & altitude/zenth angle
y2019- set year to 2019 m12 - set month to 12 (i.e. Dec.)
d31 - set day to 31 h23 - set UT hour to 23
+-65 - advance UT by +-65 minutes [nil]- refresh (get current UT)
e0/1/2/n - TDT-UT[s]=<0>/<64.184>/<64.184+(y-2001.5)*5/7>/<n>
s0/1/2/3 - Distance[AU]/Diameter[deg]/Magnitude/Ta[K](for Aeff = 804.25m^2)
f0/1/2/3 *- Phase_angle[deg]/Phase[0 to 1.0]/+-Elongation[deg]/Tb[K]
* Ta & Tb refer to freq[GHz] = 12.0; to change it enter 'f3 freq'
b0/.../10 - b0-Sun, b1-Mercury, b2-Venus, b3-Moon, b4-Mars, b5-Jupiter,
b6-Saturn, b7-Uranus, b8-Neptune, b9-Pluto, b10-E_M barycenter, b11-all
>? ż
y2003, m01, d29, e2, c1, a1, p1, n1, r0; z1, s1, f3 12.0, t0 Saturn > ż
Lat[deg] 53.0955, Long[deg] 18.5641, Height[km] 0.1336, DelT[s] 65.26 > ż
The positions are based on JPL DE405 read from the /users/kb/moon/JPL405
binary file (replaceable) valid from 1999.12.24 to 2020.01.15.
Enjoy under 1" accuracy for all the bodies (save Pluto)!
Program written by K. Borkowski of
Centre for Astronomy, Nicolaus Copernicus University
Torun, Poland (2002)
>z0 ż
9:17:00 82.0837 22.0356 82.6676 -1.2029 0.005223 105 19:04:06.5 >s3 ż
2003Jan29 82.0837 22.0356 82.6676 -1.2029 1.77 105 Saturn >f2 ż
2003Jan29 82.0837 22.0356 82.6676 -1.2029 1.77 133.60 Saturn >H ż
UT1 RA Dec EclLong EclLat Ta[K] +Elong LocalAppST >b11 ż
9:17:00 311.4759 -17.9984 309.0463 -0.0024 11600.00 0.00 Sun
2003Jan29 285.6563 -20.8558 284.6181 1.7933 1.02 -24.49 Mercury
9:17:00 262.6439 -20.3827 263.1019 2.8811 11.20 -46.02 Venus
2003Jan29 270.9621 -26.4577 270.8665 -3.0207 233.74 -38.29 Moon
9:17:00 246.1615 -21.2173 247.8699 0.4095 0.24 -61.18 Mars
2003Jan29 136.3568 17.5496 133.6378 0.8530 15.82-175.34 Jupiter
9:17:00 82.0837 22.0356 82.6676 -1.2029 1.77 133.60 Saturn
2003Jan29 330.1330 -12.9420 327.6995 -0.7117 0.08 18.67 Uranus
9:17:00 313.0444 -17.5455 310.6067 0.0346 0.02 1.56 Neptune
2003Jan29 259.0162 -13.7911 259.1987 9.2378 0.00 -50.47 Pluto >i ż
y2003, m01, d29, e2, c1, a1, p1, n1, r0; z0, s3, f2 12.0, t0 Pluto >s1 ż
2003Jan29 259.0162 -13.7911 259.1987 9.2378 0.000037 -50.47 Pluto >f3 30 ż
2003Jan29 259.0162 -13.7911 259.1987 9.2378 0.000037 80 Pluto >z2 ż
9:17:00 259.0162 -13.7911 27.8436 70.7955 0.000037 80 19:04:06.5 >b11 ż
9:17:00 311.4759 -17.9984 334.8957 74.4188 0.541280 8200 Sun
2003Jan29 285.6563 -20.8558 0.3606 73.9520 0.002086 380 Mercury
9:17:00 262.6439 -20.3827 22.5228 76.2226 0.005701 420 Venus
2003Jan29 270.9621 -26.4577 13.6412 80.6278 0.529988 231 Moon
9:17:00 246.1615 -21.2173 37.1214 81.9368 0.001439 185 Mars
2003Jan29 136.3568 17.5496 150.1540 104.6586 0.012224 145 Jupiter
9:17:00 82.0837 22.0356 202.6226 102.0468 0.005223 100 Saturn
2003Jan29 330.1330 -12.9420 315.6587 76.0463 0.000929 100 Uranus
9:17:00 313.0444 -17.5455 333.2754 74.3949 0.000599 90 Neptune
2003Jan29 259.0162 -13.7911 27.8436 70.7955 0.000037 80 Pluto >H ż
UT1 RA Dec Azimuth ZenithD Diameter Tb[K] LocalAppST
|
XII.3 Formularz propozycji obserwacji
Propozycje obserwacji na radioteleskopie RT32 należy składać na
formularzu według poniższego wzoru, który można wydrukować
z wersji
postscriptowej lub TeX-owej
(ta wersja wymaga dołączenia logo w formacie eps).
XII.4 Katalogi obiektów i mapy tła
Gęstości strumienia
radioźródeł kalibracyjnych
(Głównie wg.: Ott et al., 1994, Astr. &
Astrophys. 284, 331)
log Fν/[Jy] = a
+ b×log ν/[MHz]
+ c×log2
ν/[MHz]
|
| Źródło | Współrzędne (B1950) |
Rozmiary | Zakres [MHz] |
Współczynniki |
Strumień,
Fν/[Jy] |
| α [h m s] |
δ
[° ' "] |
["]×["] |
od do |
a | b | c |
1420 | 1665 |
5000 |
|
| 3C48 | 01 34 49.8 |
32 54 20 | 1.5×1.5 | 1408 23780 | 2.465 | –0.004 | –0.1251 | 16.2 | 14.3 | 5.5 |
| 3C123 | 04 33 55.6 | 29 33 52 | 23×5 | 1408 23780 | 2.525 | +0.246 | –0.1638 | 47.1 | 41.5 | 15.6 |
| 3C147 | 05 38 41.9 | 49 49 48 | 1×1 | 1408 23780 | 2.806 | –0.140 | –0.1031 | 21.9 | 19.3 | 7.5 |
| 3C161 | 06 24 43.0 |
–05 51 14 | 3×3 | 1408 10550 | 1.250 | +0.726 | –0.2286 | 18.5 | 16.5 | 6.4 |
| 3C218 | 09 15 41.3 | –11 53 05 | 47×15 | 1408 10550 | 4.729 | –1.025 | +0.0130 | 42.4 | 36.5 | 13.0 |
| 3C227 | 09 45 08.5 | 07 39 19 | 200×50 | 1408 4750 | 6.757 | –2.801 | +0.2969 | 7.5 | 6.5 | 2.9 |
| 3C249.1 | 11 00 25.0 | 77 15 11 | 15×15 | 1408 4750 | 2.537 | –0.565 | –0.0404 | 2.3 | 2.0 | 0.8 |
| Vir A | 12 28 17.7 | 12 40 29 | 150-250 | 1408 10550 | 4.484 | –0.603 | –0.0280 | 201.8 | 178.2 | 74.2 |
| 3C286 | 13 28 49.6 | 30 45 58 | 1.5×1.5 | 1408 43200 | 0.956 | +0.584 | –0.1644 | 14.6 | 13.5 | 7.4 |
| 3C295 | 14 09 33.5 | 52 26 13 | 5×1 | 1408 32000 | 1.490 | +0.756 | –0.2545 | 22.1 | 19.2 | 6.4 |
| 3C309.1 | 14 58 56.6 | 71 52 11 | 1.5×1.5 | 1408 32000 | 2.617 | –0.437 | –0.0373 | 7.4 | 6.6 | 3.1 |
| 3C348 | 16 48 40.8 | 05 04 36 | 170×25 | 1408 10550 | 3.852 | –0.361 | –0.1053 | 46.5 | 39.5 | 11.9 |
| 3C353 | 17 17 55.6 | –00 55 53 | 210×60 | 1408 10550 | 3.148 | –0.157 | –0.0911 | 55.9 | 49.7 | 20.9 |
| Cyg A | 19 57 44.5 | 40 35 47 | 170×45 | 4750 10550 | 8.360 | –1.565 | — | — | — | 372.5 |
| * | | | | | 4.695 | +0.085 | –0.178 | 1564. | 1323. | 374.9 |
| NGC7027‡ | 21 05 08.4 | 42 01 59 | 7×10 | 10550 43200 | 1.322 | –0.134 | — | 7.9 | 7.8 | 6.7 |
| Tau A | 05 31 30 |
21 58 00 | 120×180 |
| 3.915 |
–0.299 | — |
938.6 | 894.9 |
644.2 |
Cas Af |
23 21 12 | 58 32 35 |
240×240 |
200 30000 | 5.5847 |
–0.7448 | — |
1725. | 1532. |
675.6 |
| | |
| 20 200 | 5.3801 |
–0.6558 | — | — | — | — |
|
* Dane dla Cyg A wg. Baars et al., 1977 (Astr. & Astrophys. 61, 99),
na niższe częstości (też fale metrowe).
‡ NGC7027 ma zmienny strumień
(spadek na λ < 6 cm i wzrost
powyżej 6 cm); w tabeli podano strumień zredukowany na epokę
JD2448171 oraz dopasowanie do punktów na 2.8, 1.3 i 0.7 cm.
f Podane
strumienie Cas A dotyczą tylko roku y = 2000. Dla innych
epok, dla obu zakresów częstości, współczynniki trzeba zmodyfikować
następująco:
a' = a –
0.0080(y – 2000) oraz
b' = b + 0.00126(y
– 2000)
(por.
Borkowski
et al., 1980, Mem.S.A.It., 51, 247).
Wartości strumienia według parametrów powyższej tabeli można obliczać
posługując się programem scal (na komputerach newton i
asterix).
Osobliwe obiekty OH/IR
|
| Źródło | RA1950 |
Dec1950 |
VLSR | Częstość |
Δf |
Strumień |
| [h m s] |
[° ' "] |
[km/s] | [MHz] |
[MHz] | (1665) [Jy] |
|
| OH127.0–0.0 |
1 30 27.7 | 62 11 31.2 |
–55 |
1612 | 0.5 |
|
| W3OH | 2 23 16.4 |
61 38 57 | –44 | 1612/65/67 | 0.5 | ~200 |
| OH138.0+7.3 | 3 20 41.5 | 65 21 32.8 | –38 | 1612 | 0.5 | |
| OH141.7+3.5 | 3 29 23.6 | 60 10 04.4 | –58 | 1612 | 0.5 | |
| VY CMa | 7 20 54.7 | –25 40 12.4 | +30 | 1612/65/67 | 1.0 | ~40 |
| VX Sgr | 18 05 03.0 | –22 13 55.2 | +5 | 1612 | 0.5 | |
| OH17.7-2.0 | 18 27 39.8 | –14 31 03.9 | +61 | 1612 | 0.5 | |
| OH26.5+0.6 | 18 34 52.5 | –5 26 36.9 | +27 | 1612 | 0.5 | |
| OH39.7+1.5 | 18 56 03.9 | 6 38 49.8 | +20 | 1612 | 0.5 | |
| W49N | 19 07 49.9 | 9 01 14 | +12 | 1665/67 | 0.5 | ~350 |
| 19114+0002 | 19 11 25 |
0 02 18 |
+100 | 1612 |
0.5 | |
| VY2–2 | 19 21 59 |
9 48 00 | –50 |
1612 | 0.5 | |
| IRC+10420 | 19 24 26.7 |
11 15 10.9 | +70 |
1612/67 | 1.0 |
|
| NML Cyg | 20 44 33.8 |
39 55 57.1 | +2 |
1612/65/67 | 0.5 |
|
|
| Źródła kalibracyjne |
|
| 3C123 | 4 33 55.6 | 29 33 52 | | | | 41.5 |
| W12* | 5 39 14.3 | –1 55 57 | +10 | | | 12.2 |
| Vir A | 12 28 18 | 12 40 29 | | | | 178.2 |
| 3C286 | 13 28 49.7 | 30 45 58 | | | | 13.6 |
| 3C348 | 16 48 42 | 5 04 30 | | | | 39.5 |
|
* W12 — strumienie na częstościach
1612 i 1667 MHz wynoszą
2.97 i 15.05 Jy (dla rozdzielczości
widma ~2 kHz). |
Silniejsze źródła w linii metanolu
— CH3OH; 6668.518 MHz
(Wg: K.M. Menten, 1991, Ap.J. 380, L75)
|
| Źródło | RA1950 |
Dec1950 |
Fpeak |
VLSR |
| [h m s] |
[° ' "] |
[Jy] | [km/s] |
|
| W3(OH) | 2 23 16.4 | 61 38 57 | 3880 | –45 |
| S231 | 5 35 51.3 | 35 44 16 | 208 | –18 |
| S252 | 6 05 53.7 | 21 39 09 | 457 | 10 |
| 9.62+0.19 | 18 03 16.0 | –20 32 01 | 4870 | 6 |
| W31(1) | 18 05 40.5 | –19 52 23 | 823 | 42 |
| 23.01–0.41 | 18 31 56.7 | –9 03 18 | 439 | 77 |
| 35.20–0.73 | 18 59 13.8 | 1 09 20 | 556 | 43 |
| 43.80–0.13 | 19 09 30.8 | 9 30 47 | 152 | 42 |
| W51 | 19 21 24.4 | 14 24 48 | 979 | 57 |
| ON1 | 20 08 10.0 | 31 22 40 | 91 | 7 |
| W75N | 20 36 50.4 | 42 27 23 | 1080 | 7 |
| Cep A | 22 54 19.2 | 61 45 47 | 1420 | –4 |
| NGC7538 | 23 11 36.6 | 61 11 50 | 346 | –58 |
|
Lista pulsarów
o deklinacjach większych od –30° i strumieniach
większych od 2 mJy
na częstości 1400 MHz
[Oprac.: Wojciech Lewandowski, 10 Dec '97]
Nazwa RA Dec Period Pdot DM w50 F1400
B0031-07 B00:31:36.37 -07:38:25.30 0.9430 .4083D+00 10.9 56.7 5.8
B0136+57 J01:39:19.77 +58:14:31.85 0.2724 .1070D+02 73.8 5.2 3.1
B0138+59 J01:41:39.94 +60:09:32.28 1.2229 .3904D+00 34.8 34.9 5.4
B0148-06 J01:51:22.74 -06:35: 3.10 1.4647 .4440D+00 25.0 56.9 4.2
B0149-16 J01:52:10.86 -16:37:52.94 0.8327 .1298D+01 11.9 17.8 2.2
J0218+42 J02:18: 6.38 +42:32:16.55 0.0023 .7500D-04 61.3 0.0 16.7
B0301+19 J03:04:33.11 +19:32:50.70 1.3876 .1296D+01 15.7 58.4 3.0
B0320+39 J03:23:26.60 +39:44:53.06 3.0321 .6380D+00 25.8 42.7 3.8
B0329+54 B03:29:11.01 +54:24:36.93 0.7145 .2050D+01 26.8 6.6 166.7
B0355+54 J03:58:53.70 +54:13:13.58 0.1564 .4397D+01 57.1 3.9 5.1
B0450-18 J04:52:34.09 -17:59:23.54 0.5489 .5756D+01 39.9 28.7 9.1
B0450+55 B04:50: 0.23 +55:38:48.50 0.3407 .2366D+01 14.6 8.1 6.6
B0523+11 J05:25:56.44 +11:15:19.00 0.3544 .7362D-01 79.3 15.9 2.2
B0525+21 B05:25:51.88 +21:57: 0.38 3.7455 .4003D+02 50.9 **** 6.3
B0531+21 B05:31:31.40 +21:58:54.39 0.0334 .4210D+03 56.8 3.0 71.8
B0540+23 J05:43: 9.65 +23:29: 6.14 0.2460 .1542D+02 77.7 6.2 3.2
B0559-05 J06:01:58.98 -05:27:50.53 0.3960 .1303D+01 80.5 11.6 2.5
J0613-02 J06:13:43.97 -02:00:47.05 0.0031 .1100D-04 38.8 0.8 2.3
B0611+22 B06:11:15.70 +22:30: 0.54 0.3349 .5963D+02 96.7 6.9 3.2
B0626+24 J06:29: 5.71 +24:15:41.65 0.4766 .1997D+01 84.2 8.8 3.4
B0628-28 B06:28:51.82 -28:32:33.46 1.2444 .7107D+01 34.4 58.2 22.9
B0740-28 J07:42:49.07 -28:22:44.02 0.1668 .1681D+02 73.8 5.7 32.9
B0809+74 J08:14:59.44 +74:29: 5.79 1.2922 .1683D+00 5.8 41.4 8.8
B0818-13 J08:20:26.35 -13:50:55.20 1.2381 .2106D+01 41.0 22.1 11.3
B0820+02 B08:20:34.03 +02:08:54.30 0.8649 .1039D+00 23.6 21.2 3.3
B0823+26 B08:23:50.47 +26:47:19.40 0.5307 .1709D+01 19.5 5.8 8.1
B0834+06 J08:37: 5.64 +06:10:14.08 1.2738 .6800D+01 12.9 23.9 9.9
B0919+06 J09:22:13.97 +06:38:21.69 0.4306 .1372D+02 27.3 10.5 5.8
B0942-13 B09:42: 4.39 -13:40:52.40 0.5703 .4620D-01 12.6 6.9 2.9
B0950+08 J09:53: 9.31 +07:55:35.60 0.2531 .2291D+00 3.0 9.5 44.4
J1012+53 J10:12:33.43 +53:07: 2.66 0.0053 .1460D-04 9.0 0.0 3.3
J1022+10 J10:22: 0.57 +10:01: 0.00 0.0165 .0000D+00 10.2 0.0 2.6
B1039-19 J10:41:36.21 -19:42:13.80 1.3864 .9446D+00 33.9 61.8 3.1
B1133+16 B11:33:27.42 +16:07:36.77 1.1879 .3733D+01 4.8 31.7 28.6
B1237+25 J12:39:40.47 +24:53:49.25 1.3824 .9605D+00 9.3 51.1 12.2
J1246+22 J12:46: 0.38 +22:53: 0.00 0.4738 .0000D+00 17.9 21.0 3.2
B1257+12 B12:57:33.12 +12:57: 6.40 0.0062 .1143D-03 10.2 0.6 2.2
B1508+55 J15:09:25.72 +55:31:33.01 0.7397 .5008D+01 19.6 10.9 12.7
B1534+12 B15:34:47.68 +12:05:45.23 0.0379 .2430D-02 11.6 0.7 4.0
B1541+09 B15:41:14.35 +09:38:42.81 0.7484 .4327D+00 35.0 46.2 8.7
B1540-06 J15:43:30.17 -06:20:45.29 0.7091 .8834D+00 18.5 8.1 4.4
B1600-27 B16:00: 0.05 -27:04: 0.12 0.7783 .2920D+01 46.2 20.0 2.2
B1604-00 B16:04:37.86 +00:24:41.67 0.4218 .3061D+00 10.7 12.5 6.0
J1643-12 J16:43:38.15 -12:24:58.70 0.0046 .3300D-04 62.4 1.3 8.3
B1642-03 B16:42:24.69 -03:12:30.93 0.3877 .1781D+01 35.7 4.2 43.7
B1702-19 J17:05:36.10 -19:06:38.50 0.2990 .4138D+01 22.9 7.3 3.2
B1706-16 B17:06:33.22 -16:37:12.90 0.6531 .6309D+01 24.9 10.8 5.2
J1713+07 J17:13:49.52 +07:47:37.55 0.0046 .8520D-05 16.0 0.2 4.0
B1718-02 B17:18:20.95 -02:09:27.70 0.4777 .8700D-01 65.5 59.0 2.4
B1717-29 J17:20:34.15 -29:33: 0.15 0.6204 .7456D+00 42.6 30.0 3.6
J1730-23 J17:30:21.62 -23:04:21.62 0.0081 .1900D-04 9.6 0.7 4.8
B1730-22 J17:33:26.42 -22:28: 0.36 0.8717 .4210D-01 41.2 12.2 2.8
B1732-07 J17:35: 4.97 -07:24:52.38 0.4193 .0000D+00 73.5 7.4 2.0
B1737+13 B17:37:49.22 +13:13:29.40 0.8030 .1454D+01 48.9 32.7 2.7
B1737-30 B17:37:21.17 -30:14:10.00 0.6067 .4653D+03 153.0 38.4 2.7
B1738-08 J17:41:22.54 -08:40:32.70 2.0431 .2274D+01 74.9 29.8 3.2
J1744-23 J17:44: 0.42 -23:12: 0.00 1.6834 .0000D+00 99.0 35.0 2.1
B1742-30 J17:45:56.29 -30:40:23.60 0.3674 .1066D+02 88.4 7.2 7.3
B1745-12 B17:45:28.20 -12:59: 0.56 0.3941 .1212D+01 100.0 12.3 2.6
B1749-28 B17:49:49.27 -28:06: 0.70 0.5626 .8139D+01 50.9 7.1 122.2
B1754-24 B17:54: 0.37 -24:21: 0.40 0.2341 .1300D+02 178.0 28.8 2.2
B1756-22 B17:56: 0.23 -22:05: 0.33 0.4610 .1080D+02 177.3 6.9 2.2
B1800-21 B18:00:51.11 -21:37:17.50 0.1336 .1343D+03 233.9 20.7 2.6
B1804-08 J18:07:38.01 -08:47:43.10 0.1637 .2868D-01 112.8 6.4 7.2
B1804-27 B18:04: 0.02 -27:15: 0.40 0.8278 .1225D+02 313.3 12.6 2.8
J1808-08 J18:08: 0.03 -08:13: 0.00 0.8760 .0000D+00 151.0 29.0 3.1
B1813-26 J18:16:35.45 -26:49: 0.58 0.5929 .6650D-01 128.0 52.5 2.0
B1818-04 B18:18:13.65 -04:29: 3.88 0.5981 .6338D+01 84.4 10.1 17.4
B1819-22 J18:22:58.97 -22:56: 0.49 1.8743 .1353D+01 121.1 73.3 2.8
B1821+05 B18:21: 4.01 +05:48:47.40 0.7529 .2250D+00 67.2 10.2 2.0
B1820-30 B18:20:27.72 -30:23:16.00 0.0054 .3385D-02 86.8 0.0 5.4
B1821-19 B18:21: 2.78 -19:47: 0.29 0.1893 .5225D+01 224.3 23.4 7.9
B1821-24 J18:24:32.00 -24:52:10.75 0.0031 .1618D-02 119.8 0.2 4.4
B1822-09 J18:25:30.59 -09:35:22.80 0.7690 .5236D+02 19.5 11.7 4.0
B1826-17 J18:29:43.12 -17:51: 2.90 0.3071 .5562D+01 217.8 45.9 8.7
B1831-03 B18:31: 0.04 -03:40: 0.55 0.6867 .4150D+02 235.8 26.4 9.9
B1831-04 B18:31:46.46 -04:28: 0.59 0.2901 .1970D+00 78.8 19.7 8.6
J1835-11 J18:35: 0.23 -11:06: 0.00 0.1659 .0000D+00 132.0 7.2 3.3
B1834-10 B18:34: 8.30 -10:10: 0.44 0.5627 .1178D+02 318.0 89.0 6.0
B1839+56 J18:40:44.59 +56:40:55.60 1.6529 .1495D+01 26.5 27.1 2.3
B1839+09 B18:39:32.82 +09:09:10.50 0.3813 .1092D+01 49.1 7.9 2.2
B1839-04 B18:39:48.10 -04:02: 0.58 1.8399 .5100D+00 196.0 **** 2.1
B1842+14 B18:42:38.52 +14:51: 3.60 0.3755 .1866D+01 41.2 9.3 2.2
B1844-04 J18:47:22.83 -04:02:14.20 0.5978 .5171D+02 142.6 24.6 8.3
B1845-01 J18:48:23.60 -01:23:58.20 0.6594 .5218D+01 159.1 43.7 8.8
B1846-06 B18:46: 0.26 -06:40: 0.26 1.4513 .4570D+02 147.6 22.3 2.9
B1855+09 J18:57:36.39 +09:43:17.32 0.0054 .1784D-04 13.3 0.6 3.4
B1857-26 J19:00:47.59 -26:00:43.10 0.6122 .2042D+00 38.1 34.1 14.6
B1859+03 J19:01:31.78 +03:31: 6.25 0.6554 .7487D+01 401.2 75.2 18.3
B1900+06 B19:00: 0.20 +06:11: 0.25 0.6735 .0000D+00 530.0 76.6 2.4
B1900+01 B19:00:57.96 +01:31: 9.41 0.7293 .4032D+01 246.4 26.8 6.4
B1900-06 B19:00: 0.59 -06:36: 0.30 0.4319 .3400D+01 195.7 16.0 2.6
B1905+39 B19:05:54.70 +39:57:18.30 1.2358 .5300D+00 30.1 58.5 2.6
B1907+02 B19:07: 7.74 +02:49:56.34 0.9898 .5529D+01 172.1 12.5 2.3
B1907+10 B19:07:27.32 +10:57: 7.67 0.2836 .2636D+01 148.4 5.9 5.6
B1907+03 B19:07:39.70 +03:53: 0.30 2.3303 .4530D+01 78.8 45.2 2.3
B1907-03 B19:07:52.30 -03:14:50.70 0.5046 .2189D+01 205.5 14.7 3.0
B1911-04 B19:11:15.17 -04:45:59.70 0.8259 .4070D+01 89.4 7.5 13.1
B1913+10 B19:13: 7.30 +10:04: 0.32 0.4045 .1530D+02 246.1 35.6 2.6
B1914+09 B19:14: 9.51 +09:46: 2.72 0.2703 .2518D+01 61.4 5.1 2.2
B1915+13 J19:17:39.78 +13:53:57.06 0.1946 .7198D+01 94.5 4.5 4.8
B1918+19 B19:18:52.60 +19:43: 2.45 0.8210 .8952D+00 154.4 40.3 3.8
B1919+21 B19:19:36.16 +21:47:16.30 1.3373 .1348D+01 12.4 30.9 6.3
B1920+21 B19:20:43.97 +21:04:52.09 1.0779 .8190D+01 217.1 14.8 3.3
B1923+04 B19:23:55.56 +04:25:27.40 1.0741 .2465D+01 101.8 15.8 2.4
B1929+10 J19:32:13.90 +10:59:31.99 0.2265 .1157D+01 3.2 5.6 33.7
B1929+20 J19:32: 8.03 +20:20:46.30 0.2682 .4216D+01 211.0 18.4 3.2
B1933+16 B19:33:31.87 +16:09:58.31 0.3587 .6004D+01 158.5 9.0 26.9
B1937+21 J19:39:38.56 +21:34:59.14 0.0016 .1051D-03 71.0 0.1 26.7
B1944+17 B19:44:38.75 +17:58:15.35 0.4406 .2440D-01 16.1 13.5 4.4
B1946+35 B19:46:33.95 +35:32:38.29 0.7173 .7052D+01 129.1 19.3 16.1
B1953+50 B19:53:57.35 +50:51:53.60 0.5189 .1366D+01 31.8 6.0 2.9
B1957+20 J19:59:36.76 +20:48:15.12 0.0016 .1685D-04 29.1 0.0 2.2
B2000+40 B20:00:59.94 +40:42:26.60 0.9051 .1744D+01 128.0 24.8 5.9
B2003-08 J20:06:16.31 -08:07: 0.02 0.5809 .4520D-01 32.1 13.2 2.2
B2011+38 B20:11:21.56 +38:36:38.00 0.2302 .8855D+01 238.6 22.7 2.9
B2016+28 B20:16: 0.17 +28:30:30.11 0.5580 .1494D+00 14.2 14.9 34.9
B2020+28 B20:20:33.28 +28:44:42.97 0.3434 .1893D+01 24.6 12.0 7.9
B2021+51 B20:21:25.31 +51:45: 7.64 0.5292 .3066D+01 22.6 7.4 8.6
B2027+37 B20:27:31.21 +37:34: 5.30 1.2168 .1230D+02 189.0 22.3 2.0
B2043-04 B20:43:22.44 -04:32:25.00 1.5469 .1476D+01 35.9 20.8 2.2
B2045-16 J20:48:35.47 -16:16:44.45 1.9616 .1096D+02 11.5 84.2 12.9
B2053+36 B20:53:33.24 +36:18:49.60 0.2215 .3648D+00 97.5 7.2 3.1
B2106+44 J21:08:20.47 +44:41:48.79 0.4149 .8619D-01 139.9 27.2 2.9
B2110+27 B21:10:54.21 +27:41:37.99 1.2029 .2623D+01 24.7 13.0 2.0
B2111+46 J21:13:24.29 +46:44: 8.68 1.0147 .7115D+00 141.5 32.1 25.6
J2145-07 J21:45:50.44 -07:50:17.90 0.0161 .0000D+00 9.0 1.2 5.6
B2148+63 B21:48:36.79 +63:15:40.00 0.3801 .1681D+00 128.0 18.1 3.6
B2154+40 J21:57: 1.82 +40:17:45.88 1.5253 .3426D+01 70.6 38.6 11.7
B2217+47 J22:19:48.13 +47:54:53.83 0.5385 .2765D+01 43.5 7.5 12.3
B2224+65 J22:25:52.36 +65:35:33.78 0.6825 .9655D+01 36.2 21.1 2.4
B2255+58 J22:57:57.71 +59:09:14.95 0.3682 .5754D+01 151.1 14.8 3.8
B2303+30 B23:03:34.09 +30:43:48.61 1.5759 .2896D+01 49.9 17.4 2.7
B2306+55 J23:08:13.83 +55:47:36.07 0.4751 .2020D+00 47.0 26.9 2.1
B2310+42 J23:13: 8.57 +42:53:12.98 0.3494 .1155D+00 17.3 8.8 9.9
J2317+14 J23:17: 9.23 +14:39:31.22 0.0034 .2420D-05 21.9 0.4 2.1
B2319+60 J23:21:55.19 +60:24:30.70 2.2565 .7037D+01 94.8 **** 4.0
B2327-20 J23:30:26.80 -20:05:28.60 1.6436 .4626D+01 8.4 17.2 4.7
|
Wyciąg z katalogu Kühra i in.
— źródła o F > 3 Jy na 5 GHz |
|
(H. Kühr et al., 1981, A.&A. Suppl.
45, 367) |
|
| Źródło |
RA1950 |
Dec1950 |
F | f |
Typ | z |
| IAU | 3C |
h | m | s |
° | ' |
" |
Jy | MHz |
|
| 0040+51 | 3C20.0 | 0 | 40 | 19 | 51 | 47 | 7 | 4,00 | 4950 | GAL | 0,35 |
| 0106+13 | 3C33 | 1 | 6 | 12 | 13 | 2 | 33 | 5,50 | 5005 | GAL | 0,05 |
| 0134+32 | 3C48 | 1 | 34 | 49 | 32 | 54 | 21 | 5,00 | 5000 | QSO | 0,36 |
| 0537–44 | | 1 | 37 | 21 | –44 | 6 | 45 | 3,67 | 4973 | QSO | 0,89 |
| 0220+42 | 3C66.0 | 2 | 20 | 2 | 42 | 46 | 27 | 3,50 | 4950 | GAL | 0,02 |
| 0305+03 | 3C78 | 3 | 5 | 49 | 3 | 55 | 14 | 3,25 | 5002 | GAL | 0,02 |
| 0316+41 | 3C84.0 | 3 | 16 | 29 | 41 | 19 | 52 | 17,00 | 5000 | GAL | 0,01 |
| 0320–37 | | 3 | 20 | 42 | –37 | 25 | 0 | 49,00 | 5000 | GAL | 0,006 |
| 0356+10 | 3C98 | 3 | 56 | 10 | 10 | 17 | 34 | 4,00 | 5005 | GAL | 0,03 |
| 0409–75 | | 4 | 9 | 58 | –75 | 14 | 57 | 4,00 | 5006 | EF | 0,00 |
| 0430+05 | 3C120 | 4 | 30 | 31 | 5 | 14 | 60 | 6,67 | 4898 | GAL | 0,03 |
| 0433+29 | 3C123 | 4 | 33 | 55 | 29 | 34 | 14 | 16,00 | 5000 | GAL | 0,21 |
| 0438–43 | | 4 | 38 | 43 | –43 | 38 | 54 | 6,00 | 4987 | QSO | 2,85 |
| 0518+16 | 3C138.0 | 5 | 18 | 16 | 16 | 35 | 27 | 4,00 | 5000 | QSO | 0,75 |
| 0518–45 | | 5 | 18 | 18 | –45 | 49 | 39 | 15,00 | 5000 | GAL | 0,03 |
| 0521–36 | | 5 | 21 | 12 | –36 | 30 | 17 | 9,00 | 5009 | GAL | 0,05 |
| 0538+49 | 3C147.0 | 5 | 38 | 43 | 49 | 49 | 43 | 8,00 | 4950 | QSO | 0,54 |
| 0637–75 | | 6 | 37 | 23 | –75 | 13 | 34 | 5,33 | 5009 | QSO | 0,65 |
| 0742+10 | | 7 | 42 | 48 | 10 | 18 | 33 | 4,00 | 5009 | EF | 0,00 |
| 0809+48 | 3C196.0 | 8 | 9 | 59 | 48 | 22 | 7 | 4,00 | 4950 | QSO | 0,87 |
| 0831+55 | | 8 | 31 | 4 | 55 | 44 | 41 | 5,00 | 4933 | GAL | 0,24 |
| 0834–20 | | 8 | 34 | 24 | –20 | 6 | 30 | 3,50 | 5005 | QSO | 2,74 |
| 0915–11 | 3C218.0 | 9 | 15 | 41 | –11 | 52 | 49 | 13,50 | 5009 | GAL | 0,05 |
| 0951+69 | 3C231.0 | 9 | 51 | 42 | 69 | 54 | 60 | 4,00 | 4950 | GAL | 0,001 |
| 1127–14 | | 11 | 27 | 35 | –14 | 32 | 55 | 6,00 | 5006 | QSO | 1,18 |
| 1216+06 | 3C270.0 | 12 | 16 | 50 | 6 | 6 | 0 | 8,50 | 5005 | GAL | 0,007 |
| 1226+02 | 3C273.0 | 12 | 26 | 33 | 2 | 19 | 43 | 42,50 | 5005 | QSO | 0,15 |
| 1228+12 | 3C274.0 | 12 | 28 | 17 | 12 | 40 | 1 | 72,33 | 5003 | GAL | 0,004 |
| 1253–05 | 3C279.0 | 12 | 53 | 35 | –5 | 31 | 8 | 15,00 | 5009 | QSO | 0,53 |
| 1322–42 | | 13 | 22 | 36 | –42 | 48 | 24 | 103,00 | 5000 | GAL | 0,002 |
| 1328+30 | 3C286 | 13 | 28 | 49 | 30 | 45 | 59 | 7,00 | 5000 | QSO | 0,84 |
| 1409+52 | 3C295.0 | 14 | 9 | 33 | 52 | 26 | 13 | 6,50 | 4950 | GAL | 0,46 |
| 1549–79 | | 15 | 49 | 27 | –79 | 5 | 23 | 3,25 | 5007 | | 0,00 |
| 1610–77 | | 16 | 10 | 51 | –77 | 9 | 52 | 3,50 | 5007 | QSO | 1,71 |
| 1641+39 | 3C345.0 | 16 | 41 | 17 | 39 | 54 | 11 | 5,00 | 5000 | QSO | 0,59 |
| 1648+05 | 3C348.0 | 16 | 48 | 40 | 5 | 4 | 32 | 11,75 | 5007 | GAL | 0,15 |
| 1717–00 | 3C353.0 | 17 | 17 | 55 | 0 | 55 | 54 | 22,00 | 5003 | GAL | 0,03 |
| 1814–63 | | 18 | 14 | 46 | –63 | 47 | 0 | 4,00 | 5009 | GAL | 0,06 |
| 1828+48 | 3C380.0 | 18 | 28 | 13 | 48 | 42 | 41 | 6,50 | 4950 | QSO | 0,69 |
| 1845+79 | 3C390.3 | 18 | 45 | 45 | 79 | 42 | 45 | 4,00 | 4950 | GAL | 0,05 |
| 1932–46 | | 19 | 32 | 18 | –46 | 27 | 24 | 3,33 | 5006 | GAL | 0,00 |
| 1934–63 | | 19 | 34 | 47 | –63 | 49 | 35 | 5,67 | 5006 | GAL | 0,18 |
| 2104–25 | | 21 | 4 | 24 | –25 | 39 | 6 | 4,33 | 5006 | GAL | 0,03 |
| 2134+00 | | 21 | 34 | 5 | 0 | 28 | 25 | 11,50 | 4980 | QSO | 1,93 |
| 2145+06 | | 21 | 45 | 36 | 6 | 43 | 41 | 3,75 | 4980 | QSO | 0,99 |
| 2153–69 | | 21 | 53 | 1 | –69 | 55 | 46 | 11,50 | 5005 | GAL | 0,02 |
| 2200+42 | | 22 | 0 | 39 | 42 | 2 | 8 | 4,00 | 4585 | BL | 0,07 |
| 2203–18 | | 22 | 3 | 25 | –18 | 50 | 17 | 4,00 | 5009 | QSO | 0,61 |
| 2223–05 | 3C446.0 | 22 | 23 | 11 | –5 | 12 | 18 | 4,00 | 5009 | QSO | 1,40 |
| 2230+11 | | 22 | 30 | 7 | 11 | 28 | 23 | 3,50 | 5005 | QSO | 1,03 |
| 2251+15 | 3C454.3 | 22 | 51 | 29 | 15 | 52 | 54 | 13,00 | 4943 | QSO | 0,85 |
| 2356–61 | | 23 | 56 | 24 | –61 | 11 | 40 | 7,33 | 5006 | GAL | 0,09 |
|
Wyciąg z katalogu Kühra i in. (1981)
— źródła o F > 3 Jy w paśmie L |
|
| Źródło |
RA1950 |
Dec1950 |
F | f |
Typ | z |
| IAU | 3C |
h | m | s |
° | ' |
" |
Jy | MHz |
|
| 0008–42 | | 0 | 8 | 21 | –42 | 9 | 33 | 3,50 | 1445 | GAL | 0,00 |
| 0023–26 | | 0 | 23 | 18 | –26 | 18 | 52 | 9,00 | 1410 | | 0,00 |
| 0034–01 | 3C15 | 0 | 34 | 30 | –1 | 25 | 39 | 4,00 | 1403 | GAL | 0,07 |
| 0035–02 | 3C17 | 0 | 35 | 47 | –2 | 24 | 7 | 6,00 | 1403 | GAL | 0,22 |
| 0038+09 | 3C18 | 0 | 38 | 14 | 9 | 46 | 55 | 4,00 | 1400 | GAL | 0,18 |
| 0040+51 | 3C20.0 | 0 | 40 | 19 | 51 | 47 | 7 | 11,50 | 1400 | GAL | 0,35 |
| 0043–42 | | 0 | 43 | 55 | –42 | 24 | 6 | 8,00 | 1410 | GAL | 0,00 |
| 0045–25 | | 0 | 45 | 5 | –25 | 33 | 41 | 6,00 | 1410 | GAL | 0,001 |
| 0055–01 | 3C29 | 0 | 55 | 1 | –1 | 39 | 46 | 4,67 | 1403 | GAL | 0,04 |
| 0104+32 | 3C31 | 1 | 4 | 41 | 32 | 8 | 7 | 4,33 | 1490 | GAL | 0,01 |
| 0105–16 | 3C32 | 1 | 5 | 48 | –16 | 20 | 21 | 4,00 | 1400 | GAL | 0,00 |
| 0106+13 | 3C33 | 1 | 6 | 12 | 13 | 2 | 33 | 12,60 | 1510 | GAL | 0,05 |
| 0114–21 | | 1 | 14 | 25 | –21 | 7 | 53 | 4,00 | 1410 | GAL | 0,00 |
| 0117–15 | 3C38 | 1 | 17 | 59 | –15 | 35 | 57 | 5,00 | 1400 | QSO | 0,00 |
| 0123–01 | 3C40 | 1 | 23 | 30 | –1 | 39 | 15 | 5,33 | 1403 | GAL | 0,01 |
| 0131–36 | | 1 | 31 | 38 | –36 | 44 | 40 | 5,00 | 1410 | GAL | 0,03 |
| 0133+20 | 3C47 | 1 | 33 | 40 | 20 | 42 | 16 | 3,25 | 1470 | QSO | 0,42 |
| 0134+32 | 3C48 | 1 | 34 | 49 | 32 | 54 | 21 | 14,25 | 1535 | QSO | 0,36 |
| 0202+14 | | 2 | 2 | 7 | 14 | 59 | 51 | 3,33 | 1400 | QSO | 0,00 |
| 0210+86 | 3C61.1 | 2 | 10 | 43 | 86 | 4 | 17 | 6,00 | 1400 | QSO | 0,18 |
| 0213–13 | 3C62 | 2 | 13 | 11 | –13 | 13 | 24 | 4,50 | 1405 | GAL | 0,00 |
| 0220+42 | 3C66.0 | 2 | 20 | 2 | 42 | 46 | 27 | 9,00 | 1490 | GAL | 0,02 |
| 0235–19 | | 2 | 35 | 24 | –19 | 45 | 29 | 4,00 | 1410 | GAL | 0,00 |
| 0237–23 | | 2 | 37 | 52 | –23 | 22 | 6 | 6,50 | 1445 | QSO | 2,22 |
| 0252–71 | | 2 | 52 | 27 | –71 | 16 | 49 | 4,00 | 1410 | GAL | 0,00 |
| 0255+05 | 3C75 | 2 | 55 | 4 | 5 | 50 | 41 | 6,33 | 1403 | GAL | 0,02 |
| 0305+03 | 3C78 | 3 | 5 | 49 | 3 | 55 | 14 | 7,00 | 1403 | GAL | 0,02 |
| 0307+16 | 3C79 | 3 | 7 | 11 | 16 | 54 | 42 | 5,00 | 1403 | GAL | 0,25 |
| 0315+41 | 3C83.1 | 3 | 15 | 0 | 41 | 41 | 12 | 8,00 | 1400 | GAL | 0,02 |
| 0316+16 | | 3 | 16 | 9 | 16 | 17 | 41 | 8,00 | 1403 | EF | 0,00 |
| 0316+41 | 3C84.0 | 3 | 16 | 29 | 41 | 19 | 52 | 16,50 | 1670 | GAL | 0,01 |
| 0325+02 | 3C88 | 3 | 25 | 18 | 2 | 23 | 22 | 4,67 | 1403 | GAL | 0,03 |
| 0349–27 | | 3 | 49 | 31 | –27 | 53 | 30 | 6,00 | 1410 | GAL | 0,06 |
| 0356+10 | 3C98 | 3 | 56 | 10 | 10 | 17 | 34 | 10,67 | 1403 | GAL | 0,03 |
| 0403–13 | | 4 | 3 | 14 | –13 | 16 | 21 | 4,00 | 1403 | QSO | 0,57 |
| 0404+03 | 3C105 | 4 | 4 | 48 | 3 | 32 | 50 | 5,00 | 1403 | GAL | 0,08 |
| 0407–65 | | 4 | 7 | 58 | –65 | 52 | 49 | 16,00 | 1410 | QSO | 0,00 |
| 0409–75 | | 4 | 9 | 58 | –75 | 14 | 57 | 14,00 | 1410 | EF | 0,00 |
| 0410+11 | 3C109 | 4 | 10 | 55 | 11 | 4 | 47 | 4,00 | 1400 | GAL | 0,30 |
| 0427–53 | | 4 | 27 | 57 | –53 | 56 | 8 | 5,00 | 1410 | GAL | 0,03 |
| 0428+20 | | 4 | 28 | 6 | 20 | 31 | 9 | 3,33 | 1431 | GAL | 0,21 |
| 0430+05 | 3C120 | 4 | 30 | 31 | 5 | 14 | 60 | 5,50 | 1519 | GAL | 0,03 |
| 0433+29 | 3C123 | 4 | 33 | 55 | 29 | 34 | 14 | 47,50 | 1400 | GAL | 0,21 |
| 0438–43 | | 4 | 38 | 43 | –43 | 38 | 54 | 5,33 | 1433 | QSO | 2,85 |
| 0442–28 | | 4 | 42 | 36 | –28 | 15 | 12 | 7,00 | 1410 | GAL | 0,00 |
| 0453–20 | | 4 | 53 | 14 | –20 | 38 | 59 | 4,00 | 1410 | GAL | 0,03 |
| 0518+16 | 3C138.0 | 5 | 18 | 16 | 16 | 35 | 27 | 8,20 | 1510 | QSO | 0,75 |
| 0518–45 | | 5 | 18 | 18 | –45 | 49 | 39 | 70,00 | 1410 | GAL | 0,03 |
| 0521–36 | | 5 | 21 | 12 | –36 | 30 | 17 | 17,00 | 1410 | GAL | 0,05 |
| 0538+49 | 3C147.0 | 5 | 38 | 43 | 49 | 49 | 43 | 20,25 | 1535 | QSO | 0,54 |
| 0605+48 | 3C153.0 | 6 | 5 | 44 | 48 | 4 | 49 | 4,00 | 1400 | GAL | 0,27 |
| 0625–53 | | 6 | 25 | 19 | –53 | 39 | 26 | 5,00 | 1410 | GAL | 0,05 |
| 0625–35 | | 6 | 25 | 20 | –35 | 27 | 20 | 4,00 | 1410 | GAL | 0,00 |
| 0637–75 | | 6 | 37 | 23 | –75 | 13 | 34 | 5,00 | 1410 | QSO | 0,65 |
| 0651+54 | 3C171.0 | 6 | 51 | 11 | 54 | 12 | 50 | 3,50 | 1400 | GAL | 0,23 |
| 0802+24 | 3C192 | 8 | 2 | 35 | 24 | 18 | 32 | 4,33 | 1490 | GAL | 0,06 |
| 0806–10 | 3C195.0 | 8 | 6 | 29 | –10 | 19 | 9 | 4,00 | 1405 | GAL | 0,00 |
| 0809+48 | 3C196.0 | 8 | 9 | 59 | 48 | 22 | 7 | 13,50 | 1405 | QSO | 0,87 |
| 0831+55 | | 8 | 31 | 4 | 55 | 44 | 41 | 8,00 | 1440 | GAL | 0,24 |
| 0834–19 | | 8 | 34 | 55 | –19 | 41 | 22 | 4,00 | 1445 | | 0,00 |
| 0915–11 | 3C218.0 | 9 | 15 | 41 | –11 | 52 | 49 | 44,50 | 1405 | GAL | 0,05 |
| 0917+45 | 3C219.0 | 9 | 17 | 50 | 45 | 51 | 44 | 7,50 | 1400 | GAL | 0,17 |
| 0939+14 | 3C225 | 9 | 39 | 28 | 14 | 2 | 35 | 4,00 | 1400 | EF | 0,00 |
| 0945+07 | 3C227.0 | 9 | 45 | 8 | 7 | 39 | 19 | 7,67 | 1403 | GAL | 0,08 |
| 0951+69 | 3C231.0 | 9 | 51 | 42 | 69 | 54 | 60 | 7,50 | 1535 | GAL | 0,001 |
| 0958+29 | 3C234 | 9 | 58 | 57 | 29 | 1 | 37 | 4,67 | 1490 | GAL | 0,18 |
| 1005+07 | 3C237.0 | 10 | 5 | 22 | 7 | 44 | 59 | 6,33 | 1403 | EF | 0,00 |
| 1127–14 | | 11 | 27 | 35 | –14 | 32 | 55 | 6,25 | 1423 | QSO | 1,18 |
| 1136–13 | | 11 | 36 | 38 | –13 | 34 | 7 | 4,00 | 1405 | QSO | 0,55 |
| 1142+19 | 3C264 | 11 | 42 | 29 | 19 | 53 | 15 | 5,67 | 1403 | GAL | 0,02 |
| 1151–34 | | 11 | 51 | 49 | –34 | 48 | 48 | 5,50 | 1445 | QSO | 0,25 |
| 1157+73 | 3C268.1 | 11 | 57 | 45 | 73 | 17 | 28 | 6,50 | 1400 | GAL | 0,00 |
| 1216+06 | 3C270.0 | 12 | 16 | 50 | 6 | 6 | 0 | 18,67 | 1403 | GAL | 0,007 |
| 1222+13 | 3C272.1 | 12 | 22 | 31 | 13 | 9 | 46 | 6,00 | 1403 | GAL | 0,003 |
| 1226+02 | 3C273.0 | 12 | 26 | 33 | 2 | 19 | 43 | 43,25 | 1397 | QSO | 0,15 |
| 1228+12 | 3C274.0 | 12 | 28 | 17 | 12 | 40 | 1 | 217,50 | 1400 | GAL | 0,004 |
| 1245–19 | | 12 | 45 | 45 | –19 | 42 | 58 | 5,00 | 1445 | QSO | 0,00 |
| 1251–12 | 3C278.0 | 12 | 51 | 59 | –12 | 17 | 13 | 7,50 | 1405 | GAL | 0,01 |
| 1253–05 | 3C279.0 | 12 | 53 | 35 | –5 | 31 | 8 | 10,00 | 1405 | QSO | 0,53 |
| 1254+47 | 3C280.0 | 12 | 54 | 41 | 47 | 36 | 33 | 5,00 | 1400 | QSO | 0,00 |
| 1306–09 | | 13 | 6 | 2 | –9 | 34 | 32 | 4,00 | 1405 | | 0,00 |
| 1308–22 | 3C283.0 | 13 | 8 | 57 | –22 | 0 | 42 | 5,00 | 1445 | GAL | 0,00 |
| 1323+32 | | 13 | 23 | 57 | 32 | 9 | 44 | 4,00 | 1575 | GAL | 0,00 |
| 1328+25 | 3C287 | 13 | 28 | 15 | 25 | 24 | 38 | 6,33 | 1490 | QSO | 1,05 |
| 1328+30 | 3C286 | 13 | 28 | 49 | 30 | 45 | 59 | 13,75 | 1538 | QSO | 0,84 |
| 1332–33 | | 13 | 32 | 58 | –33 | 37 | 54 | 5,00 | 1410 | GAL | 0,01 |
| 1345+12 | | 13 | 45 | 6 | 12 | 32 | 20 | 5,00 | 1423 | GAL | 0,12 |
| 1350+31 | 3C293 | 13 | 50 | 3 | 31 | 41 | 33 | 4,00 | 1535 | GAL | 0,04 |
| 1358+62 | | 13 | 58 | 58 | 62 | 25 | 8 | 4,00 | 1440 | GAL | 0,00 |
| 1409+52 | 3C295.0 | 14 | 9 | 33 | 52 | 26 | 13 | 22,50 | 1405 | GAL | 0,46 |
| 1414+11 | 3C296.0 | 14 | 14 | 24 | 11 | 1 | 53 | 4,00 | 1403 | GAL | 0,02 |
| 1416+06 | 3C298.0 | 14 | 16 | 38 | 6 | 42 | 21 | 5,75 | 1423 | QSO | 1,43 |
| 1420+19 | 3C300 | 14 | 20 | 41 | 19 | 48 | 55 | 3,67 | 1403 | GAL | 0,27 |
| 1453–10 | | 14 | 53 | 12 | –10 | 56 | 51 | 5,00 | 1400 | QSO | 0,93 |
| 1458+71 | 3C309.1 | 14 | 58 | 56 | 71 | 52 | 11 | 8,00 | 1400 | QSO | 0,90 |
| 1502+26 | 3C310 | 15 | 2 | 46 | 26 | 12 | 35 | 6,67 | 1490 | GAL | 0,05 |
| 1508–05 | | 15 | 8 | 14 | –5 | 31 | 49 | 3,50 | 1405 | QSO | 1,19 |
| 1508+08 | 3C313.0 | 15 | 8 | 33 | 8 | 2 | 58 | 4,00 | 1400 | GAL | 0,00 |
| 1511+26 | 3C315 | 15 | 11 | 30 | 26 | 18 | 40 | 3,67 | 1490 | GAL | 0,10 |
| 1549–79 | | 15 | 49 | 27 | –79 | 5 | 23 | 5,00 | 1410 | | 0,00 |
| 1559+02 | 3C327.0 | 15 | 59 | 58 | 2 | 6 | 16 | 8,67 | 1403 | GAL | 0,10 |
| 1602+01 | 3C327.1 | 16 | 2 | 12 | 1 | 25 | 59 | 4,00 | 1403 | GAL | 0,00 |
| 1607+26 | | 16 | 7 | 9 | 26 | 49 | 19 | 4,25 | 1424 | EF | 0,00 |
| 1609+66 | 3C330.0 | 16 | 9 | 16 | 66 | 4 | 31 | 7,00 | 1400 | GAL | 0,54 |
| 1610–77 | | 16 | 10 | 51 | –77 | 9 | 52 | 4,00 | 1410 | QSO | 1,71 |
| 1634+62 | 3C343.0 | 16 | 34 | 1 | 62 | 51 | 42 | 4,33 | 1427 | QSO | 0,98 |
| 1637–77 | | 16 | 37 | 9 | –77 | 10 | 2 | 5,00 | 1410 | GAL | 0,02 |
| 1637+62 | 3C343.1 | 16 | 37 | 55 | 62 | 40 | 34 | 4,00 | 1400 | GAL | 0,75 |
| 1641+39 | 3C345.0 | 16 | 41 | 17 | 39 | 54 | 11 | 8,50 | 1670 | QSO | 0,59 |
| 1648+05 | 3C348.0 | 16 | 48 | 40 | 5 | 4 | 32 | 46,00 | 1403 | GAL | 0,15 |
| 1717–00 | 3C353.0 | 17 | 17 | 55 | 0 | 55 | 54 | 57,33 | 1403 | GAL | 0,03 |
| 1733–56 | | 17 | 33 | 22 | –56 | 31 | 57 | 8,00 | 1410 | QSO | 0,00 |
| 1814–63 | | 18 | 14 | 46 | –63 | 47 | 0 | 13,00 | 1410 | GAL | 0,06 |
| 1828+48 | 3C380.0 | 18 | 28 | 13 | 48 | 42 | 41 | 14,00 | 1535 | QSO | 0,69 |
| 1842+45 | 3C388.0 | 18 | 42 | 35 | 45 | 30 | 21 | 5,00 | 1400 | GAL | 0,09 |
| 1845+79 | 3C390.3 | 18 | 45 | 45 | 79 | 42 | 45 | 11,50 | 1400 | GAL | 0,05 |
| 1932–46 | | 19 | 32 | 18 | –46 | 27 | 24 | 13,00 | 1410 | GAL | 0,00 |
| 1934–63 | | 19 | 34 | 47 | –63 | 49 | 35 | 16,00 | 1410 | GAL | 0,18 |
| 1938–15 | | 19 | 38 | 24 | –15 | 31 | 35 | 7,00 | 1405 | GAL | 0,00 |
| 1939+60 | 3C401.0 | 19 | 39 | 38 | 60 | 34 | 33 | 4,00 | 1400 | GAL | 0,20 |
| 1949+02 | 3C403.0 | 19 | 49 | 44 | 2 | 22 | 42 | 5,67 | 1403 | GAL | 0,05 |
| 1954–55 | | 19 | 54 | 19 | –55 | 17 | 41 | 6,00 | 1410 | GAL | 0,00 |
| 2032–35 | | 20 | 32 | 37 | –35 | 4 | 30 | 5,00 | 1410 | GAL | 0,00 |
| 2058–28 | | 20 | 58 | 39 | –28 | 13 | 49 | 5,00 | 1410 | GAL | 0,03 |
| 2104–25 | | 21 | 4 | 24 | –25 | 39 | 6 | 13,00 | 1410 | GAL | 0,03 |
| 2104+76 | 3C427.1 | 21 | 4 | 45 | 76 | 21 | 4 | 3,50 | 1400 | GAL | 0,00 |
| 2121+24 | 3C433 | 21 | 21 | 30 | 24 | 51 | 15 | 11,67 | 1403 | GAL | 0,10 |
| 2128+04 | | 21 | 28 | 2 | 4 | 49 | 4 | 4,00 | 1430 | EF | 0,00 |
| 2153–69 | | 21 | 53 | 1 | –69 | 55 | 46 | 27,50 | 1410 | GAL | 0,02 |
| 2153+37 | 3C438.0 | 21 | 53 | 45 | 37 | 46 | 14 | 6,33 | 1490 | GAL | 0,00 |
| 2200+42 | | 22 | 0 | 39 | 42 | 2 | 8 | 6,00 | 1400 | BL | 0,07 |
| 2203–18 | | 22 | 3 | 25 | –18 | 50 | 17 | 6,00 | 1403 | QSO | 0,61 |
| 2211–17 | 3C444.0 | 22 | 11 | 42 | –17 | 16 | 34 | 9,00 | 1405 | GAL | 0,00 |
| 2221–02 | 3C445.0 | 22 | 21 | 15 | –2 | 21 | 57 | 6,00 | 1400 | GAL | 0,05 |
| 2223–05 | 3C446.0 | 22 | 23 | 11 | –5 | 12 | 18 | 6,00 | 1405 | QSO | 1,40 |
| 2230+11 | | 22 | 30 | 7 | 11 | 28 | 23 | 6,83 | 1460 | QSO | 1,03 |
| 2243+39 | 3C452.0 | 22 | 43 | 31 | 39 | 25 | 31 | 10,50 | 1400 | GAL | 0,08 |
| 2250–41 | | 22 | 50 | 12 | –41 | 13 | 44 | 4,00 | 1410 | GAL | 0,00 |
| 2251+15 | 3C454.3 | 22 | 51 | 29 | 15 | 52 | 54 | 11,33 | 1403 | QSO | 0,85 |
| 2314+03 | 3C459 | 23 | 14 | 2 | 3 | 48 | 55 | 4,33 | 1403 | GAL | 0,22 |
| 2331–41 | | 23 | 31 | 45 | –41 | 42 | 2 | 5,00 | 1410 | GAL | 0,00 |
| 2335+26 | 3C465 | 23 | 35 | 55 | 26 | 44 | 37 | 7,00 | 1490 | GAL | 0,03 |
| 2356–61 | | 23 | 56 | 24 | –61 | 11 | 40 | 26,00 | 1410 | GAL | 0,09 |
|
|
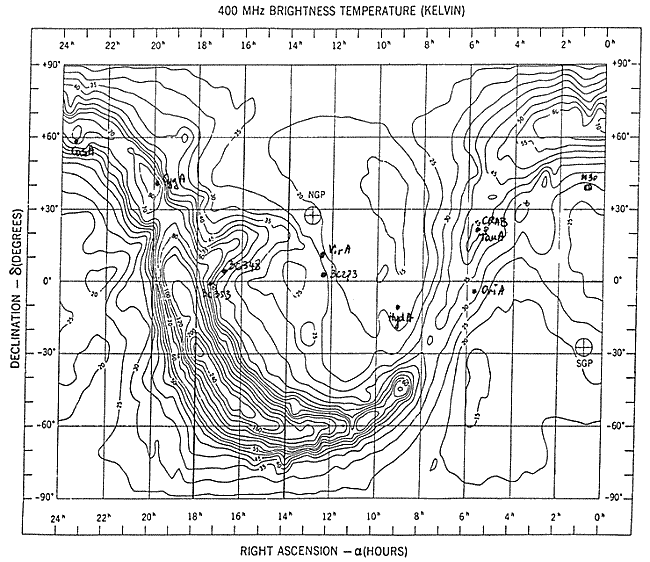
Mapa nieba na częstotliwości 400 MHz
|
File translated from
TEX
by
TTH,
version 3.40 on 06 Aug 2003.