This is preprint of a paper published in Class. Quantum Grav.,
vol. 22, No 18 (21 September 2005), S1243–S1254
An all-sky search of EXPLORER data
-
P Astone†,
D Babusci‡,
M Bassan§,
K M Borkowski#,
L Brocco||,
E Coccia§,
S D'Antonio§,
V Fafone‡,
S Frasca||,
G Giordano‡,
P Jaranowski£,
A Królak$ * @,
A Marini‡,
Y Minenkov§,
I Modena§,
G Modestino‡,
A Moleti§,
A Pai†,
G V Pallottino||,
C Palomba†,
M Piêtka£,
G Pizzella¶,
L Quintieri‡,
F Ricci||,
A Rocchi§,
F Ronga‡,
R Terenzi+ and
M Visco+
† Istituto Nazionale di Fisica Nucleare INFN, Rome, Italy
‡ Istituto Nazionale di Fisica Nucleare INFN, Frascati, Italy
§ University of Rome "Tor Vergata" and INFN, Rome II, Italy
|| University of Rome "La Sapienza" and INFN, Rome, Italy
¶ University of Rome "Tor Vergata" and INFN, Frascati, Italy
+ IFSI-CNR and INFN, Rome
# Center for Astronomy, Nicolaus Copernicus University,
Toruñ, Poland
£ Institute of Theoretical Physics, University of Bia³ystok,
Bia³ystok, Poland
$ Albert Einstein Institute, Golm, Germany
Abstract
We have analyzed three data sets, each 2 days long, of the EXPLORER
resonant bar detector. We have searched for continuous gravitational-wave
signals from spinning neutron stars. Our data analysis technique was based
on the maximum likelihood detection method. We briefly describe the theoretical methods
that we used in our search and we present results of the search.
The main outcome of our analysis is an upper limit of 1×10-22
for the dimensionless amplitude of a continuous gravitational-wave signal.
The upper limit is for any source location in the sky, any polarization of the wave
and for signals of frequency from 921.00 Hz to 921.76 Hz and with
spin down from -2.36 ×10-8 Hz s-1 to +2.36 ×10-8 Hz s-1. |
Contents
1 Introduction
2 Data analysis methods
2.1 Response of a bar detector to a continuous gravitational-wave signal
2.2 Optimal data analysis method
2.3 An approximate model
2.4 Search strategy
2.5 False alarm probability, detection probability, grid of templates
3 An all-sky search of EXPLORER data
3.1 Parameter space
3.2 Data selection
3.3 Results
4 Upper limit
Acknowledgments
References
1 Introduction
When we observe a continuous gravitational-wave signal by a ground
based detector for a sufficiently long time its phase and
amplitude are modulated due to the motion of the detector with
respect to solar system barycenter. Therefore detecting such a signal
and estimating its parameters enables determination of the
position of the source of the wave. Further, in the data from a
single detector gravitational waves from all sky locations are
registered. This enables an all-sky search for continuous
gravitational waves with a single detector. The difficulty in the
search for gravitational-wave signals is that they are very weak
and they are deeply buried in the noise of the detector.
Consequently the detection of these signals and interpretation of
data analysis results is a delicate task. In this paper we present
results of an all-sky search for continuous sources of
gravitational radiation. A prime example of such a source is a
spinning neutron star. A signal from such a source has definite
characteristics that make it suitable for application of the
optimal detection techniques based on matched filtering. Moreover
such signals are stable as a result of the stability of the
rotation of the neutron star and they will be present in the data
for time periods much longer than the observational interval. This
enables a reliable verification of the potential candidates by
repeating the observations both by the same detector and by
different detectors.
In our all-sky search we have used the data of the EXPLORER
resonant bar detector [1]. A
directed search of the galactic center with the EXPLORER detector
has already been carried out and an upper limit for the amplitude
of the gravitational waves has been established [2].
This paper is organized as follows. In Section 2 we summarize the
theoretical tools that we use in our analysis, in Section 3 we present
results of our all-sky search, and in Section 4 we derive the main result
of our analysis which is an upper limit for the dimensionless amplitude
of continuous gravitational waves from spinning neutron stars.
This is a revised upper limit with respect to one we previously reported
for a shorter period [7].
The data analysis was performed by a team consisting of Pia Astone, Kaz
Borkowski, Piotr Jaranowski, Andrzej Królak and Maciej Piêtka and was carried
out on the basis of a Memorandum of Understanding between the ROG collaboration
and Institute of Mathematics of Polish Academy of Sciences. More details about
the search can be found in [9].
2 Data analysis methods
In this section we give a summary of data analysis techniques that we used in
the search. More details are given in Refs. [3,4,5,6,7].
2.1 Response of a bar detector to a continuous gravitational-wave signal
The dimensionless noise-free response function h of a resonant bar
gravitational-wave detector to a weak plane gravitational wave in
the long wavelength approximation [i.e., when the size of the
detector is much smaller than the reduced wavelength
l/(2p)
of the wave] can be written in the following form
where Ai are four constant amplitudes that depend on amplitude
ho and phase fo of the wave and two polarization angles
i and y.
The time dependent functions hi have the form
|
|
|
h1(t) = a(t) cosF(t), h2(t) = b(t) cosF(t), | |
|
h3(t) = a(t) sinF(t), h4(t) = b(t) sinF(t). |
|
|
|
| | (2) |
|
The functions a and b are amplitude modulation functions
(see Eqs. (3) of [7]), and F is the phase modulation
(see Eq. (6) of [7]). The amplitude modulations a and
b depend on the right ascension a and the declination
d of the source and they are varying with a period of 1
sidereal day. The phase F depends on the frequency
w0, the s spin-down parameters wk
(k=1,¼,s), and on the angles a, d. We call
the parameters w0, wk, a, d the
intrinsic parameters and the remaining ones the extrinsic
parameters. As we shall see in the following Section we only need
to search for signals over the intrinsic parameter space. The
whole signal h depends on s + 7 unknown parameters: ho,
fo, i, y, a, d, w0,
wk. The response also depends on the position of the
detector with respect to the solar system barycenter (SSB). This
position can be determined with a great accuracy using JPL
Planetary and Lunar Ephemerides DE405/LE405.
2.2 Optimal data analysis method
Assuming that the noise in the detector is an additive,
stationary, Gaussian, and zero-mean random process we can derive
the optimum matched filter for the signal given in Section
2.1. Under a simplifying assumption that the
observation time To is an integer multiple of one sidereal day
and assuming that over the bandwidth of the signal h the
spectral density Sh(f) of the detector's noise is
constant and equal to Sh(f0), where f0 is the frequency of
the signal measured at the SSB at the beginning time of the
analysis, the application of the matched filter reduces to evaluating
the F-statistic given by
|
F = |
2
Sh(f0) To
|
|
æ
è
|
|Fa|2
áa2ñ
|
+ |
|Fb|2
áb2ñ
|
ö
ø
|
, |
| (3) |
where
| |
|
Fa : = |
ó
õ
|
To
0
|
x(t) a(t) exp[-iF(t)] dt, |
|
|
Fb : = |
ó
õ
|
To
0
|
x(t) b(t) exp[-iF(t)] dt. |
|
|
|
| | (4) |
|
In Eq. (4) x(t) is the h-reconstructed data and
á ·
ñ denotes time averaging over the observational
interval [0,To].
The F-statistic given above depends only on the intrinsic
parameters whereas the estimators of the four amplitudes Ai are
given in an explicit analytic form:
|
|
^
A
|
1
|
= 2 |
áx h1ñ
áa2ñ
|
, |
^
A
|
2
|
= 2 |
áx h2ñ
áb2ñ
|
, |
^
A
|
3
|
= 2 |
áx h3ñ
áa2ñ
|
, |
^
A
|
4
|
= 2 |
áx h4ñ
áb2ñ
|
. |
| (5) |
The estimators of the signal
parameters are obtained in two steps. Firstly, the estimators of
the intrinsic parameters (frequency, spin-down parameters, and
the angles a and d) are obtained by maximizing the
functional F with respect to these parameters. Secondly, the
estimators of the amplitudes Ai are calculated from the
analytic formulas (5) with the correlations
áx hiñ
evaluated for the values of the parameters obtained in the first
step.
2.3 An approximate model
In order to calculate the F-statistic efficiently we
introduced an approximation to the phase F(t)
of the signal consisting
of expansion of the motion of the Earth around the Sun in a Taylor
series. We find that for a 2-day long data set the following
approximation is satisfactory:
|
Ys(t) = p + p0 t + p1 t2 + A cos(Wr t) + B sin(Wr t), |
| (6) |
where Wr is the rotational angular velocity of the
Earth. The characteristic feature of the above approximation is
that the phase is a linear function of the parameters of the
signal. The parameters A and B are related to the right
ascension a and the declination d of the
gravitational-wave source through the equations
|
|
|
A = |
w0 r
c |
cosd
cos(a - fr), |
|
|
B = |
w0 r
c |
cosd
sin(a - fr), |
|
|
|
| (7) |
where w0 is the angular frequency of the
gravitational-wave signal and r is the equatorial component
of the detector's radius vector with respect to the center of the Earth.
The parameters p, p0, and p1 contain contributions both from
the intrinsic evolution of the gravitational-wave source
and the modulation of the signal due to the motion of the Earth
around the Sun.
2.4 Search strategy
With the above approximation the integrals given by Eqs. (4) that we needed to
compute in order to evaluate F are Fourier transforms and they can be efficiently
calculated using the FFT algorithm. Thus the evaluation of
F consists of correlation of the data with two linear filters
depending on parameters p1, A, B followed by FFTs. In Ref. [6]
we have verified that for the case of our search the linear approximation
to the phase does not produce a loss in signal-to-noise ratio
of more than 5%. The linear approximation is the better the shorter the
observation time, the narrower the bandwidth and the higher the frequency
of the signal.
In order to identify potential gravitational-wave signals we apply a two step
procedure consisting of a coarse search followed by a fine search.
The coarse search consists of evaluation of F on a discrete grid in the intrinsic
parameter space and comparison
of the obtained values of F with a predefined threshold Fo.
The grid is constructed in such a way that the loss of the signal-to-noise is minimized.
The parameters of the nodes of the grid for which the threshold is crossed are
registered. These events are called triggers of our search.
The threshold is calculated from a chosen false alarm probability which is defined
as the probability that
F crosses the threshold when no signal is present and the data is only noise.
The fine search consists of finding a local maximum of F for each trigger
using a numerical
implementation of the Nelder-Mead algorithm [10],
where coordinates of the starting
point of the maximization procedure are the parameter values of the coarse search.
2.5 False alarm probability, detection probability, grid of templates
To calculate the false alarm probability as a function of the threshold and to
construct a grid in the parameter space we introduce yet another approximation
of our signal. Namely we use a signal with a constant amplitude and the phase
given by Eq. (6). In paper [4] we have shown that the
Fisher matrix for the exact model with amplitude modulations given by Eq. (1) can be accurately reproduced by the Fisher matrix of a constant
amplitude model. As the calculations of the false alarm probability and
construction of a grid in the parameter space are based on the Fisher matrix we
expect that the constant amplitude model is a good approximation for the purpose
of the above calculations. We stress that in the search of real data we used
the full model with amplitude modulations.
False alarm probability PTF(Fo) is the probability that the
F-statistic crosses a threshold Fo and is given by
|
PTF(Fo) = 1 -
[1 -
PF(Fo)]Nc , |
| (8) |
where Nc
is the number of cells in the parameter space, i.e., the number of
statistically independent realizations of the F-statistic when
the data is only noise and PF is false alarm probability for a
single cell. If the detector noise is Gaussian, 2F has c2
distribution with 4 degrees of freedom and PF is given by
|
PF(Fo) = (1 + Fo) exp(-Fo). |
| (9) |
Probability of
detection PD(d,Fo) is the probability that a signal with
signal-to-noise ratio d crosses the threshold Fo and it is
given by
|
PD(d,Fo) : = |
ó
õ
|
¥
Fo
|
p1(d,F) dF, |
| (10) |
where (here I1 is the modified Bessel
function of the first kind and order 1)
|
p1(d,F) = |
d
|
I1 |
æ
è
|
d |
Ö
|
2F
|
|
ö
ø
|
exp |
æ
è
|
-F
– |
1
2
|
d2 |
ö
ø
|
. |
| (11) |
We choose the grid of templates in such a way that the correlation
C between any potential signal present in the data and the
nearest point of the grid never falls below a certain value. In
the case of the approximate model of the signal that we use the
grid is uniform and consists of regular polygons in the space
parameterized by p0, p1, A, B. The construction of the grid is
described in detail in Section VIIA of [2]. For the grid
that we used in the search of the EXPLORER data the correlation
function C for any signal present in the data was greater than
0.77.
3 An all-sky search of EXPLORER data
We have implemented the theoretical tools presented in Section
2 and we have performed an all-sky search for
continuous sources of gravitational waves in the data of the
resonant bar detector EXPLORER 1 [1]. The detector has
collected many years of data with a high duty cycle (e.g. in 1991
the duty cycle was 75%). The EXPLORER detector was, in the year
1991, most sensitive for two narrow bandwidths (called minus and
plus modes) of about 1 Hz wide at two frequencies around
1 kHz 2. To
make the search computationally manageable we analyzed two days of
data in the narrow band where the detector had the best
sensitivity. To narrowband the data we use the FFT data base in
which EXPLORER data are stored and extract the data by doing
inverse FFT of the Fourier data for a bandwidth of our choice. The
procedure of extraction a narrow band sequence from FFT data base
is described in detail in [2], Appendix C. By narrowing
the bandwidth of the search we can shorten the length of the data
to be analyzed as we need to sample the data at the rate of only
twice the bandwidth [8].
For the sake of the FFT algorithm it is best to keep
the length of the data to be a power of 2. Consequently we have
chosen the number of data points to analyze to be N = 218. Thus
for To = 2 days of observation time the bandwidth Dn
was Dn = N/(2To) ~ 0.76 Hz.
We analyzed the data around the plus
resonance of the system, because in the chosen period it was
most sensitive, compared to the minus resonance.
The same analysis could be repeated around the minus resonance
As a result we searched
the bandwidth from 921.00 Hz to 921.76 Hz. We have included 1 spin down
parameter in the search and we have searched the spin down range
from -2.36×10-8 Hz s-1 to +2.36×10-8 Hz s-1.
We have first searched one 2 day stretch of data.
The first results of that analysis were reported in [7].
We have then performed two further searches of 2 day stretches of data.
3.1 Parameter space
We have used the filters with the phase linear in the parameters
given by Eq. (6). In the filters we have included the
amplitude modulation. The number of cells Nc in parameter space
which is the number
of independent realizations of the statistic F when there is no
signal in the data was around 1.6 ×1012.
Consequently from Eq. (8) the threshold
signal-to-noise ratio for 1% false alarm probability was equal to
8.3. In the search that we have performed we have used a lower
threshold signal-to-noise of 6.7. The aim of lowering the
threshold was to make up for the loss of the signal-to-noise ratio
due the discreteness of the grid of templates and due to the use
of filters that only approximately matched the true signal. The
number of points in the grid over which we had to calculate the
statistic F turned out to be 183 064 440. This number
involved 63 830 positions in the sky and 2 868 spin down
values for each sky position.
3.2 Data selection
The two-day stretches of data that we have analyzed were taken from
a larger set of 13 days of data taken by the EXPLORER detector
in November 1991. We have first carried out a characterization
of the data. We have divided the data into 216 points sections corresponding
to around 11 hours of data. For each stretch we
have obtained a box-and-whisker plot, we have estimated spectral
density, and we have performed the Kolmogorov-Smirnov (KS) test.
The box-and-whisker plots display the amount of outliers present in the data.
Each box has lines at the lower quartile, median,
and upper quartile values of the data stretch.
The whiskers are lines extending from each end of the box
to show the extent of the rest of the data.
Outliers are data with values beyond the ends of the whiskers
and they are marked by a + sign.
The whisker extends to the most extreme data
value within 1.5 interquartile range of the box.
Spectral density gives us sensitivity of the detector at a given frequency.
The KS test calculates the KS distance between the sample distribution and
the Gaussian distribution and test the null hypothesis that the
data come from the Gaussian distribution. The output of the test
is the p-value which is the probability of observing the
KS distance under the null hypothesis. Thus the higher
the p-value the more "Gaussian" the data are.

| Figure 1:
Quality of the EXPLORER data. The x-axis gives the
number of the 11-hour block of data from the 13-day data run.
The top panel are the box plots for each block of data. The middle
panel is the spectrogram of the data. Spectrogram contains
spectrum of each block of data. The bottom panel gives results of
the KS test. The vertical lines indicate beginning and end of each
search that we have performed. |
The results of the characterization of our data are presented in Figure 1.
From the KS test we conclude that large parts of our data
are approximately Gaussian. We have chosen the three
2-day long stretches of data on the basis of conformity of the data
to the Gaussian random distribution.
The stretches we have chosen are marked by vertical lines in Figure 1.
The Modified Julian Dates of first samples of the three sets are
48580.7909, 48590.3221, and 48582.7854 respectively.
In Figure 2 we have presented
the spectral densities of the two day stretches of data that we have chosen.
We see that the minimum spectral density was close to 10-42/Hz.

Figure 2:
Two-sided spectral density of the three 2-day stretches
of EXPLORER data that were analyzed. |
3.3 Results
| Search | Northern hemisphere | Southern hemisphere |
| I | 15663 | 21601 |
| II | 9883 | 11666 |
| III | 18776 | 23850 |
| Table 1:
Number of triggers for the three searches of EXPLORER data. |
In Table 1 we present numbers of triggers in the
three searches for threshold corresponding to
signal-to-noise ratio of 6.7. We recall that this threshold is lower
than the threshold of 8.3 corresponding to false alarm probability
of 1%. In Figure 3
we have plotted the histograms of the values of the F-statistic
for the independent candidates and we have compared them with the
theoretical distribution for F when no signal is present in the
data. We see that we obtain a good agreement with the theoretical
distribution of (1/2) c2 with 4 degrees of freedom only for the
first set of data that we have analyzed. The other two data sets
show non-Gaussian behavior which is most prominent for the third
set.
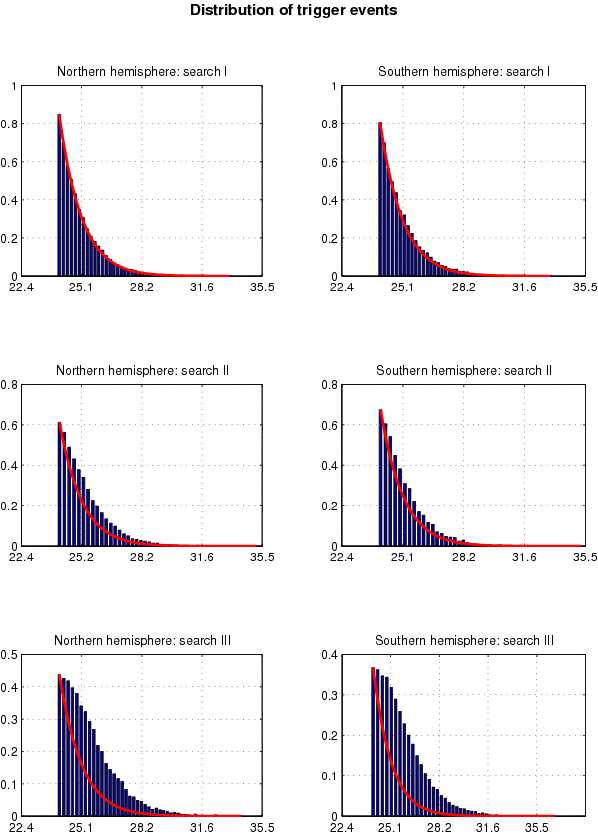
| Figure 3:
Histograms of the values of the F-statistic of triggers for
the 3 searches of EXPLORER data.
The solid line corresponds to the theoretical (1/2) c2
distribution with 4 degrees of freedom.
The x-axis gives values of the F-statistic. |
The next step of our analysis is the verification of the triggers
using filters based on the accurate model of the signal
presented in the previous section.
The verification procedure consisted of 5 steps.
- Fine search using the linear filter.
- Fine search with accurate templates
that includes precise detector ephemeris.
- Fine search for the signal in
another 2-day stretch of the available data.
- Fine search of a 4-day stretch of data
consisting of the original one and the 2-day stretch
of data following it.
- Fine search in the whole data set
In the first search no event has crossed our 99% confidence
threshold of 8.285. In the second search there was one event
crossing, however the event has not crossed the threshold of 6.7
in a different data set and in the 4-day stretch the event has
not even crossed the threshold of 6.7. For the third search there
were 76 threshold crossings. There were no corresponding
crossings of the threshold of 6.7 in a different data set and for
4 days of observation time highest increase in signal-to-noise
ratio was 5%. Typically the signal-to-noise ratio for 4 days
has decreased by around 15%. Consequently we can attribute the
8.285 threshold crossings to non-Gaussian behavior of the noise
as the 99% confidence of this threshold was calculated assuming
the data were Gaussian.
The results of the verification procedure for one of the triggers
are presented in Figure 4. A trigger
of signal-to-noise ratio 7.4, crossing of a low threshold of 6.7,
occurred. In astrophysical parametrization an event of signal-to-noise
ratio of 7.3, crossing our threshold also occurred.
There was an event in a different
stretch of data of somewhat lower signal-to-noise ratio of 6.7.
However for 4 days of data signal-to-noise ratio decreased with
respect to the signal-to-noise for 2 days. Consequently we do not
consider this trigger as a gravitational-wave signal candidate.

| Figure 4:
An example of verification
procedure of a trigger signal. The 4 panels are plots of
F-statistic as a function of frequency. Signal-to-noise ratios
and confidence levels corresponding to maxima of the
F-statistic are given. The threshold corresponding to 1% false
alarm probability is drawn by a horizontal thick line. The thin
horizontal line denotes lowered threshold equivalent to
signal-to-noise ratio of 6.7. For four days verification
procedure the thin vertical line correspond to signal-to-noise
ratio equal to Ö2 × 6.7. The left top panel is for
approximate linear parametrization of the signal, the right top
panel is for astrophysical parameters. Note the difference in the
frequency of the trigger for the two panels. The frequency in
linear parametrization contains contribution from the motion of
the Earth around the Sun. The left bottom panel is the result of
verification of the trigger in a different data set. The right
bottom panel is verification in a twice as long data set. The
trigger is not considered as a gravitational-wave candidate
because it is not a significant signal in the 2-day search and its
signal-to-noise ratio does not increase when we increase the
observation time by a factor of 2. In fact the signal-to-noise
ratio decreased by 5% instead of increasing (theoretically by a
factor of Ö2). |
In order to make sure that we do not miss any real signals among
our trigger events we have carried out the verification procedure
of all the triggers in the whole 13-day long data set available for
us. If any of the triggers were a true gravitational-wave signal we
should have obtained very strong signals of SNR equal to 17 or
more. The largest signal-to-noise ratio we obtained for all three
searches was 7.7.
In Table 2 we have given values of maximum signal-to-noise
for all events at various stages of search and verification procedure
and for all the 3 searches that we have performed.
| Maximal signal-to-noise ratios |
| Search
|
|
| Astrophysical |
| parametrization |
|
|
|
|
| I | 8.01 | 8.19 | 7.68 | 8.02 | 7.35 |
| II | 8.28 | 8.29 | 8.05 | 7.91 | 7.48 |
| III | 8.48 | 8.45 | 7.38 | 8.90 | 7.70 |
| Table 2:
Maximal signal-to-noise ratios of events at various
stages of data analysis procedure. The maxima are quoted for each
stage of the search separately and in general they correspond to different
triggers. "Linear parametrization" means search
using linear parametrization introduced in Section 2.3,
ästrophysical parametrization" means verification using astrophysical
parameters and precise ephemeris of the detector, "different data"
denotes verification in a different set of data, "longer data"
means verification in 4-day stretch of data, "all data" means
verification in the whole 13-day set of data. |
4 Upper limit
As we do not have a detection of a gravitational-wave signal we
can make a statement about the upper bound for the
gravitational-wave amplitude. We calculate our upper limit
assuming Gaussian distribution of the detector's noise. We take a
threshold value Fo of the F-statistic corresponding to the
signal-to-noise ratio do of the loudest trigger obtained in the
search, i.e., Fo = 2 + (1/2) do2. Then, using formula
(10) for detection probability, we calculate the
signal-to-noise dul of the gravitational-wave signal so that
there is probability P that it crosses threshold
Fo; dul is the desired P confidence upper
limit. For several independent searches the relation between the
confidence P and upper limit dul is given by
|
P = 1 - |
L
Õ
i = 1
|
|
æ
è
|
1 - PD(dul,Foi) |
ö
ø
|
, |
| (12) |
where Foi is the threshold corresponding to loudest
event in ith search and L is number of searches. Here
P is the probability that a signal of signal-to-noise ratio
dul crosses the threshold Foi for at least one of the
L independent searches.
In order to translate our upper limit for the signal-to-noise
ratio to upper limit hul for gravitational-wave amplitude we assume
that our source of a continuous gravitational wave is a spinning
neutron star modelled as a triaxial ellipsoid. Since we have
searched the whole sky we cannot assume a particular position of
the source and a specific polarization of the gravitational wave.
Therefore to relate amplitude of the wave and the signal-to-noise
ratio we used the averaged expression given by Eq. (93) of
[3]. Moreover as we do not know the frequency of the
gravitational-wave signal for spectral density we take its average
Šo over the bandwidth.
Thus hul and dul are related by the following formula:
Assuming confidence of 90% and taking the signal-to-noise ratios of loudest
events for astrophysical parametrization equal to 8.19, 8.29, and 8.45
for searches I, II, and III, respectively, we find that for the 1st
search dul = 9.5 whereas for all three searches dul = 8.5.
This corresponds to average dimensionless amplitudes
of 1.0×10-22 and 9.4×10-23 respectively.
Since in the first search the data conformed very well to a Gaussian
distribution we consider the upper limit for the first search as the
most reliable.
Consequently we have the following conclusion from our search:
In the frequency band from 921.00 Hz to 921.76 Hz,
for spin-down range from -
2.36×10-
8 Hz s-
1
to +2.36×10-8 Hz s-
1, and for
signals coming from any sky direction and of any polarization, the dimensionless amplitude
of the gravitational wave from a continuous source is less
than 1×10-
22 with 90% confidence.
This upper limit is higher than the one we previously reported
[7]. The reason is that in [7] to evaluate the upper
limit on amplitude we used maximal gravitational-wave amplitude
and the minimal spectral density of the detector noise instead of
the average quantities that we use here. In [11] a more
sophisticated method to determine the upper limit was developed.
In [11] instead of assuming Gaussian distribution of the
data the probability of detection was obtained by injecting
signals to the data.
Acknowledgments
The work of P. Jaranowski, A. Królak, K. M. Borkowski, and
M. Piêtka was supported in part by the KBN (Polish State
Committee for Scientific Research) Grant No. 1 P03B 029 27. We
would also like to thank Interdisciplinary Center for Mathematical
and Computational Modelling of Warsaw University for computing
time.
References
- [1]
-
Astone P 1993
Phys. Rev. D 47 362
- [2]
-
Astone P 2002
Phys. Rev. D 65 022001
- [3]
-
Jaranowski P, Królak A and Schutz B F 1998
Phys. Rev. D 58 063001
- [4]
-
Jaranowski P and Królak A 1999
Phys. Rev. D 59 063003
- [5]
-
Jaranowski P and Królak A 2000
Phys. Rev. D 61 062001
- [6]
-
Astone P, Borkowski K M, Jaranowski P and Królak A 2002
Phys. Rev. D 65 042003
- [7]
-
Astone P 2003
Class. Quantum Grav. 20 S665-S676
- [8]
-
Tretter S A 1976
Introduction to discrete time signal processing,
John Wiley & sons, New York
- [9]
-
http://www.astro.uni.torun.pl/~kb/AllSky/AllSky.html
- [10]
-
Lagarias J C, Reeds J A, Wright M H and Wright P E 1998
SIAM J. Optimization 9 112
- [11]
-
LIGO Scientific Colaboration: Abbott B 2004
Phys. Rev. D 69 082004
*
On leave of absence from Institute of Mathematics Polish Academy of Sciences,
Warsaw, Poland.
@
krolan@aei.mpg.de
1 The EXPLORER detector
is operated by the ROG collaboration of the Italian Istituto
Nazionale di Fisica Nucleare (INFN).
2 In 2000 the EXPLORER detector was upgraded and
its high sensitivity was extended to a bandwidth of 10 Hz.
File translated from
TEX
by
TTH, v. 3.72 on 8 Feb 2006.




