PHYSICAL REVIEW D
Vol. 65 (2002), 042003 (18 pp.)
Data analysis of gravitational-wave signals
from spinning neutron stars
IV. An all-sky search |
Pia Astone
Istituto Nazionale di Fisica Nucleare,
(INFN)-Rome I, 00185 Rome, Italy
Kazimierz M. Borkowski
Center for Astronomy,
Nicolaus Copernicus University,
Gagarina 11, 87-100 Toruń, Poland
Piotr Jaranowski
Institute of Theoretical Physics,
University of Białystok,
Lipowa 41, 15-424 Białystok, Poland
Andrzej Królak
Institute of Mathematics, Polish Academy of Sciences,
Śniadeckich 8, 00-950 Warsaw, Poland
(Received 29 December 2000, published 25 January 2002)
|
We develop a set of data analysis tools for a realistic all-sky search for
continuous gravitational-wave signals and we test our tools against simulated
data. The aim of the paper is to prepare for analysis of the real data from the
EXPLORER bar detector, however the methods that we present apply both to data
from the resonant bar detectors that are currently in operation and the laser
interferometric detectors that are in the final stages of construction and
commissioning. With our techniques we shall be able to perform an all-sky
coherent search of 2 days of data from the EXPLORER detector for frequency
bandwidth of 0.76 Hz in one month with 250 Mflops computing power.
This search will detect all the continuous gravitational-wave signals with
the dimensionless amplitude larger than 2.8×10–23 with
99% confidence, assuming that the noise in the detector is Gaussian.
|
|
PACS number(s): 95.55.Ym, 04.80.Nn, 95.75.Pq, 97.60.Gb |
I. INTRODUCTION AND SUMMARY
It was shown that an all-sky full frequency bandwidth coherent search of data of
many months duration for continuous gravitational-wave signals is
computationally too prohibitive to be realized with presently available
computing power [1,2]. Consequently two alternative approaches
emerge. One that we shall call tracking involves tracking of lines in
the time-frequency plane built from the Fourier transforms of one day long
stretches of data [3,4]. The other that we shall call
stacking involves dividing the data into a day long stretches, searching each
stretch for signals, and enhancing the detectability by incoherently summing the
Fourier transforms of data stretches [5]. In this paper we develop data
analysis tools for the first stage of the stacking approach, namely for the
coherent search of a few days long stretches of data. These tools involve
storage of the data in the Fourier domain database, calculation of the precise
position of the detector with respect to the solar system barycenter using JPL
ephemeris, calculation of the detection thresholds, approximation of the signal
by a simple linear model, and construction of the grid of templates in the
parameter space ensuring that the loss of signals due to the finite spacing of
the grid is minimized.
In this theoretical work we have in mind a particular set of data, namely the
data collected by the EXPLORER bar detector. This detector is most sensitive
over certain two narrow bandwidths of about 1 Hz wide at frequency around 1 kHz.
To make the search computationally feasible we propose an all-sky search of a
few days long stretches of data in the narrow band where the detector has the
best sensitivity. We find that with a 250 Mflops of computing power we can
carry out a complete all-sky search in around a month for signals within a
bandwidth of 0.76 Hz at frequency of 922 Hz and for observation time of 2 days.
We assume that the minimum characteristic time for the change of the signal's
frequency is 1000 years. By our search we shall be able to detect all the
continuous gravitational-wave signals with the parameters given above and with
the dimensionless amplitude larger than
2.8×10–23 with 99% confidence.
The tools developed in this work can be applied not only to the analysis of the
bar data but also to the interferometer data. In the case of the wide-band
interferometer one can divide the data into many narrow bands and analyze each
band using the algorithms presented in this paper.
The plan of the paper is as follows.
In Sec. II we present responses of a
laser interferometer and a resonant bar to a continuous gravitational wave,
including the effects of both amplitude and frequency modulation of the
response. The optimal data processing method is described in Sec. III.
In Sec. IV we introduce the frequency domain
database and in Sec. V we discuss how to calculate the precise
position of the detector with respect to the solar system barycenter.
In Sec. VI we introduce an approximate model of the detector's response called
the linear model and we describe its performance. In Sec. VII we
construct a grid of templates in the parameter space, we calculate the
computational requirements to do the search, and we perform Monte Carlo
simulations to test the performance of our grid and our search algorithm. In
Sec. VIII we discuss and choose parameters for our planned all-sky
search of the EXPLORER detector data. Several details are presented in the
Appendices.
Many methods presented in this paper rely on general analytic tools developed in
a previous paper of this series [6] that we shall call Paper III.
|
II. DETECTOR'S NOISE-FREE RESPONSE
Dimensionless noise-free response function h of the gravitational-wave
detector to a weak plane gravitational wave in the long wavelength approximation
[i.e. when the size of the detector is much smaller than the reduced wavelength
λ/(2π) of the wave] can be written as a linear combination of the
wave polarization functions h+ and h×:
|
h(t) = F+(t) h+(t) + F×(t) h×(t), |
| (2.1) |
where F+ and F× are called the beam-pattern functions.
Explicit formulas for the interferometric and the bar beam-pattern
functions can be found in Appendix A, where we
have also included the derivation of the beam-pattern functions for the
bar detector.
We are interested in a continuous gravitational wave described by the wave
polarization functions of the form
where h0+ and h0× are the amplitudes of the two independent wave
polarizations, Ψ is the phase of the wave.
The amplitudes h0+ and h0× depend on the physical mechanisms
generating the gravitational wave. In the case of a wave originating from a
spinning neutron star which possesses some static deviation from axisymmetry
(supported by the solid crust or by the star's own magnetic field) these
amplitudes can be estimated by
where I is the neutron star moment of inertia with respect to the rotation
axis, ε is the gravitational ellipticity of the
star, r is the
distance to the star, and f the frequency of the gravitational wave. The
value of 10–5 of the parameter
ε in the above estimate should be
treated as an upper bound. In reality it may be several orders of magnitude
less. A different mechanism like for example Chadrasekhar-Friedman-Schutz
instability would give a different dependence of the amplitude on frequency of
the wave.
The phase Ψ of the wave is given by
|
|
|
|
(2.4a) |
|
|
|
|
s1
Σ
k=0
|
ωk |
tk+1
(k+1)!
|
+ |
n0·rSSB(t)
c
|
|
s2
Σ
k=0
|
ωk |
tk
k!
|
, |
|
(2.4b) |
|
where Φ0 is the initial phase of
the wave form, rSSB is the
vector joining the solar system barycenter (SSB) with the detector, and n0 is the constant unit vector in the direction from the
SSB to the neutron star. We assume that the gravitational wave form is
almost monochromatic around some angular frequency
ω0 which we define as instantaneous
angular frequency evaluated at the SSB at t = 0,
ωk (k = 1,2,…)
is the k-th time derivative of the instantaneous angular frequency at the SSB
evaluated at t = 0. To obtain formulas (2.4) we model the
frequency of the signal in the rest frame of the neutron star by a Taylor
series. For the detailed derivation of the phase model
(2.4) see Sec. II B and Appendix
A of Ref. [2]. The integers s1 and
s2 are the number of spin
downs to be included in the two components of the phase. We need to include
enough spin downs so that we have a sufficiently accurate model of the signal
to extract it from the noise. This will depend on the length of the
observation time.
It is convenient to decompose the response h of the gravitational-wave
detector (both resonant bar and laser interferometer) described by Eqs. (2.1), (2.2), and (2.4) [cf. also Eqs. (A1) and
(A10) in Appendix A]
into a linear combination of several components:
where the four constant amplitudes Ai are given by
|
|
|
|
sinζ(h0+cos2ψcosΦ0 – h0×sin2ψsinΦ0), |
|
(2.6a) | |
|
|
sinζ(h0×cos2ψsinΦ0
+ h0+sin2ψcosΦ0), |
| (2.6b) | |
|
|
sinζ(–h0+cos2ψsinΦ0
– h0×sin2ψcosΦ0), |
|
(2.6c) | |
|
|
sinζ(h0+cos2ψcosΦ0
– h0×sin2ψsinΦ0).
|
| (2.6d) |
|
The amplitudes Ai depend, through h0+ and h0×, on the physical
mechanism generating the gravitational wave. They also depend on the initial
phase Φ0 of the wave form and the
polarization angle ψ of the wave.
The angle ζ is the angle between the interferometer
arms (usually ζ = 90°), and for the case of bars
always ζ = 90°.
The functions hi do not depend on the mechanism generating
the gravitational wave and they have the form
|
|
| (2.7a) | |
|
(2.7b) |
|
|
|
(2.7c) |
|
|
| (2.7d) |
|
where the amplitude modulation functions a and b can be found in
Appendix A
[see Eqs. (A2) for an interferometer and Eqs. (A11) for a bar],
and Φ is the phase given by
Eq. (2.4b). The functions a and b
depend on the right ascension α and the
declination δ of the
source (they also depend on the detector's geodetic latitude
φ and the angle γ
describing the orientation of the detector with respect to local
geographical directions). The phase Φ
depends on the angular frequency ω0,
s spin-down parameters ωk
(k = 1,…,s), and on the angles
α, δ; it also depends
on the latitude φ of the
detector. We call parameters ω0,
ωk, α,
δ the phase parameters. The whole
signal h depends thus on s + 5 unknown parameters:
h0+, h0×, α,
δ, ω0, and
ωk.
The amplitude modulation, determined by the functions a and b, splits the
power spectrum of the signal into five lines corresponding to angular
frequencies ω0 – 2Ωr,
ω0 –
Ωr,
ω0,
ω0 +
Ωr, and
ω0 +
2Ωr, where
Ωr is the
rotational angular velocity of the Earth. Moreover the maximum of the signal's
power can be in any of these components depending on the position of the source
in the sky. Therefore we need to take the amplitude modulation into
account in the design of a matched filter since a filter of constant amplitude
and matched only to the phase would mean a drastic decrease of the
signal-to-noise ratio.
|
III. OPTIMAL DATA ANALYSIS METHOD
The signal given by Eq. (2.5) will be buried in the noise of a detector.
Thus we are faced with the problem of detecting the signal and estimating its
parameters. A standard method is the method of maximum likelihood (ML)
detection that consists of maximizing the likelihood function, which we shall
denote by Λ, with respect to the parameters of the
signal. If the maximum of Λ exceeds a certain
threshold calculated from the false alarm probability that we can afford, we
say that the signal is detected. The values of the parameters that maximize
Λ are said to be the maximum likelihood
estimators of the parameters of the signal. The magnitude of the
maximum of Λ determines the probability of detection
of the signal.
In the current paper we consider the gravitational-wave signal consisting of one
narrow-band component. The ML detection of more general signal consisting of
N narrow-band components was studied in detail in Sec. III of Paper III. We
only need here to recall the main results derived in Paper III and specialize
them to the case of one-component signal. A related approach to signal
detection has also been developed by Owen [7], Mohanty and
Dhurandhar [8], and Mohanty [9].
We assume that the noise in the detector is an additive, stationary, Gaussian,
and zero-mean continuous random process. We also assume that over the frequency
bandwith of the signal the (one-sided) noise spectral density Sh(f) is nearly
constant and equal to Sh(f0), where f0 is the frequency of the signal
measured at the SSB at t = 0. Moreover, to simplify analytic formulas, we
restrict to the observation time To being an integer multiple of one
sidereal day, i.e., To =
n(2π/Ωr) for some positive integer n.
Then the analytic formulas for the ML estimators of the amplitudes Ai, cf.
Eq. (2.5), are given by (for derivation, cf. Sec. III A of Paper III)
|
(3.1a) |
|
(3.1b) |
|
(3.1c) |
|
(3.1d) |
|
where we have introduced the following notation (here [0,To] is
the observation interval)
|
<x> : = | 1
To
|
| ∫ |
To
0
|
x(t) dt. |
| (3.2) |
Explicit formulas for the time averages
<a2> and
<b2>
are given in Appendix B.
The reduced log likelihood function F can be written as
1
|
F ≈ |
2
Sh(f0) To
|
|  |
|Fa|2
<a2> |
+ |
|Fb|2
<b2> |
 |
, |
| (3.3) |
where
|
|
|
| ∫ |
To
0
|
x(t) a(t) exp[–iΦ(t)] dt, |
| (3.4a) | |
|
|
| ∫ |
To
0
|
x(t) b(t) exp[–iΦ(t)] dt. |
| (3.4b) |
|
Thus the ML detection in Gaussian noise leads to a matched filter. The ML
estimators of the signal's parameters are obtained in two steps. Firstly, the
estimators of the frequency, the spin-down parameters, and the angles α
and δ are obtained by maximizing the functional F with respect to
these parameters. Secondly, the estimators of the amplitudes Ai are
calculated from the analytic formulas (3.1) with the correlations <xhi>
evaluated for the values of the parameters obtained in the first
step. Thus filtering for the narrow-band gravitational-wave signal requires
two linear complex filters.
When the signal is absent and phase parameters are known 2F has
a χ2
distribution with four degrees of freedom and when the signal is present it has
a noncentral χ2 distribution with four degrees of freedom and
noncentrality parameter equal to the optimal signal-to-noise ratio d.
When phase parameters are unkown we can approximate F by a homogeneous
χ2 random field and divide the parameter space into elementary cells
defined by the correlation function of F (consult Sec. III B of Paper III
for details). The false alarm probability i.e. the probability PTF that
F exceeds the threshold Fo in one or more cell is given by
|
PTF(Fo) = 1
– [1 – PF(Fo)]Nc, |
| (3.5) |
where Nc is the total number of elementary cells and
|
PF(Fo) = (1 + Fo)
exp(–Fo). |
| (3.6) |
The expected number of false alarms NF is given by
The probability of detection PD i.e. the probability that F exceeds the
threshold Fo when the signal-to-noise ratio is equal to d is given by
|
PD(d,Fo) = |
∫ |
∞
Fo |
p1(d,F) dF, |
| (3.8) |
where
|
p1(d,F) = |
d
|
I1 | (
|
d |
√
|
2F
|
|
)
|
exp | (
|
–F – | 1
2
|
d2 |
)
|
, |
| (3.9) |
here I1 is the modified Bessel function of the first kind and order 1.
It will very often be the case that the filter we use to extract the signal from
the noise is not optimal. This may be the case when we do not know the exact
form of the signal (this is almost always the case in practice) or we choose a
suboptimal filter to reduce the computational cost and simplify the analysis.
For such a case in Sec. VI of Paper III we have developed a theory of
suboptimal filtering. The suboptimal statistics Fsub has the same form as
the optimal statistics F and the data analysis procedure consists of
maximizing the value of the suboptimal statistics. One can show that
|
E1{Fsub} = 1 + |
1
2
|
dsub2,
|
| (3.10) |
where E1 is the expectation value when the signal is present and
the parameter dsub is the suboptimal signal-to-noise ratio.
The formulas for the false alarm and detection probabilities have the same form
as in the case of the optimal filter except that the optimal signal-to-noise
ratio is replaced by the suboptimal one. Also for the suboptimal filter the
number of cells Nsc may be different than for the optimal one. Thus the
false alarm probability is given by
|
PTsF(Fo) = 1 –
[1 – PF(Fo)]Nsc.
|
| (3.11) |
The expected number of false alarms NsF reads
The detection probability takes the form
|
PD(dsub,Fo) = |
∫
|
∞
Fo |
p1(dsub,F)
dF, |
| (3.13) |
where the probability density function p1 is given by
Eq. (3.9). Equation (3.10) implies
that maximizing expectation value of the suboptimal
statistics when the signal is present is equivalent to maximizing suboptimal
signal-to-noise ratio. We can identify the maximum dsmax of
dsub as the signal-to-noise ratio of the suboptimal filter. It
was shown in Paper III that
where FF is the fitting factor introduced by Apostolatos
[10]. The fitting factor FF between a signal
h(t;θ) and a filter
h'(t;θ')
(θ and
θ' are the parameters of the
signal and the filter, respectively) is defined
as2
FF : =
|
max
θ'
|
|
(h(t;θ)|h'(t;θ'))
|
|
√
|
(h(t;θ)
|h(t;θ))
|
|
√
|
(h'(t;θ') |h'(t;θ'))
|
|
|
. |
|
(3.15) |
The fitting factor is a good measure of the quality of the suboptimal filter
however the performance of the filter can only be fully determined by
the false alarm and detection probabilities given by Eqs.
(3.11) and (3.13).
|
IV. THE FREQUENCY DOMAIN DATABASE
The data collected by the detector constitute a time series with a sampling
interval Δt. This time domain sequence can also be
stored in the
frequency domain without any loss of information. Organization of the data in
the frequency domain in a suitable way provides a very flexible database that is
very useful both for search of the data for gravitational-wave signals and for
characterization of the noise of the detector. The first step to construct
frequency domain database consists simply of taking a fast Fourier
transform (FFT) of 2N data points and
storing the first N points of the FFT. To improve the quality of the
time-domain data that will eventually be extracted from the database the
original data are windowed and overlapped. Each FFT is then normalized and
calibrated where the calibration process takes into account the transfer
function of the detector so that the units of the FFT are
strain/√(Hz). Moreover the quality of the data
represented by FFT
is characterized so that it is possible to choose thresholds for vetoing the
data or criteria to weight them. Both the calibration and the data
characterization information are stored in the header that is attached to each
FFT.
It is very important to choose a suitable number N of data in each FFT. This
depends on the type of signal search that one wants to perform. In the case of
the search for continuous sources which is a subject of this work we choose N
in such a way the maximum expected Doppler shift due to the motion of the
detector with respect to SSB is less than the width of one bin. In the case of
the EXPLORER data this leads to N = 216. For sampling time
Δt = 0.18176 s this means length of data for
each FFT of around 2/3 of an hour. Another important criterion for the choice
of the length of data interval for each FFT is that within the interval the
noise is stationary. In the case of the EXPLORER detector stationarity is in
general preserved over 2/3 of an hour intervals.
The detailed steps to create the frequency domain database and to extract
narrowband time series from the base are given in
Ref. [11].
|
V. POSITION AND VELOCITY OF THE DETECTOR WITH RESPECT TO THE SOLAR SYSTEM
BARYCENTER
A. Dealing with time scales
The data acquisition system of the detector is synchronized to the Coordinated
Universal Time (UTC) as disseminated by international time services. Thus it is
assumed that each datum corresponds to a given UTC. The UTC scale is
essentially uniform, except for occasional 1 s steps introduced internationally
to compensate for the variable Earth rotation. When these steps are taken into
account, the UTC is reduced to the International Atomic Time (TAI) scale, which
is uniform and differs from the Terrestrial Dynamical Time (TDT or TT, normally
used to describe celestial phenomena by astronomers) only by a constant term.
In principle, the time argument of positions of celestial objects is the
Barycentric Dynamical Time (TDB), however it differs from the TDT only by a very
small additive term (less than 0.001 s in magnitude), thus for all practical
purposes they do not have to be distinguished. So we have:
|
TDB ≈ TDT = TAI + 32.184 s, |
|
where TAI is obtained from UTC by removing the time steps.3 One can thus relate given UTC with barycentric
positions of all the major celestial bodies of the solar system.
However, to relate the position of a point on the Earth to the barycenter of the
Earth (the latter being obtained from the solar system ephemeris) one has to use
yet another time scale — the rotational time scale UT1, which is nonuniform and
is determined from astronomical observations. The difference
UT1 – UTC, which is maintained within
±0.90 s, is taken from
the IERS tabulations of daily values.4
B. Topocentric coordinates
To be able to relate a point on the Earth surface to the solar system barycenter
it is necessary to know orientation of the Earth in space. The primary effects
that should be taken into account are: diurnal (variable) rotation, precession
and nutation of the Earth rotational axis, and polar motion. The precession and
nutation can be accounted for by applying standard astronomical theories. The
remaining two effects are unpredictable for a longer future, so observational
data must be used.5
The polar motion is taken into account by modifying the conventional
geographical coordinates of a point on the Earth:
|
|
| =
|
φo
+ Px cosλo –
Py sinλo, |
|
(5.1a) | |
| =
| λo
+ (Pxsinλo
+ Pycosλo) tanφo, |
|
(5.1b) |
|
where φo is the conventional
geographical latitude, λo is the conventional longitude, and Px and Py are the
coordinates of the pole with respect to the Conventional International Origin.
The rotational angle of the Earth is included through conversion of UTC to UT1
(the quantity UT1 – UTC is tabulated in the IERS
files). UT1 serves to calculate the apparent sidereal time
θ, which is essentially equal to
φr +
Ωrt of
Eqs. (A2) and (A11) plus the
nutation in longitude projected on the celestial equator. The sidereal time in
turn is used to find rectangular coordinates of the point (the detector) in the
IERS celestial reference frame:
where
is the equatorial component of the radius vector,
ψ = arctan(b tanφ /a)
is the reduced latitude, h is the height above the Earth ellipsoid, and
a = 6378.140 km and b = a(1 – 1/f) (where
f = 298.257) are the semiaxes of the Earth ellipsoid. These coordinates
are affected by the polar motion through dependence of r and
ψ on φ, and
θ on λ.
The polar motion (Px and Py) and UT1
– UTC quantities are linearly
interpolated between the daily IERS values.
Since these coordinates are naturally referred to the epoch of date,
they are further precessed back to the standard epoch J2000.
The precessed Cartesian coordinates
(xE,yE,zE)2000 may now be
straightforwardly added to coordinates of the Earth barycenter with
respect to the solar system barycenter (which are described in the next
paragraph) to obtain the desired position vector of the detector.
C. Barycentric coordinates of the Earth (JPL ephemeris)
For computing the coordinates of the Earth barycenter, relative to the SSB, use
is made of the latest JPL Planetary and Lunar Ephemerides, “DE405/LE405" or
just “DE405"6,
created in 1997 and described in detail by Standish [12].
It represents an improvement over
its predecessor, DE403. DE405 is based upon the International Celestial
Reference Frame (ICRF; an earlier popular ephemeris DE200, which has been the
basis of the Astronomical Almanac since 1984, is within 0.01
arcseconds of
the frame of the ICRF). It constitutes of a set of Chebyshev polynomials fit
with full precision to a numerical integration over 1600 AD to 2200 AD. Over
this interval the interpolating accuracy is not worse than 25 meters for any
planet and not worse than 1 meter for the Moon. The JPL package allows a
professional user to obtain the rectangular coordinates of the Sun, Moon, and
nine major planets anywhere between JED 2305424.50 (1599 DEC 09) to JED
2525008.50 (2201 FEB 20).
In the application described in this paper we have used only a 21-year (1990 to
2010) subset of the original ephemeris. The ephemeris gives separately the
position of the Earth-Moon barycenter and the Moon's position relative to this
barycenter. The Earth position vector is thus calculated as a fraction
(involving the masses of the two bodies) of the Moon's one and opposite to the
latter.
Finally, the vector traveled by the Sun towards its apex (with the speed of 20
km/s) between J2000 and the epoch of observation is added to the Earth
barycentric position. The direction of solar apex is assumed at 18h
in right ascension and 30° in declination at the epoch J1900. This
direction is precessed to J2000. What is commonly known as the solar apex
refers rather to solar system barycenter apex. However since the apex motion
is known only approximately, really there is no need to distinguish between
motions of the Sun and of the barycenter.
D. Velocities
Although the primary concern in this project is to convert positions, the
velocity of the gravitational-wave detector relative to the SSB may prove to be
useful in future analyzes of spectra obtained from the acquired data.
The velocity of the detector is the sum of diurnal rotational motion of the
Earth, Earth motion in space relative to the SSB, and motion of the solar system
itself towards the apex. The last of the named components, towards the apex,
has been described in the previous paragraph. The Earth barycentric velocity
vector is obtained directly from the JPL ephemeris along with the position
vector. Finally, the detector motion relative to the Earth barycenter is
represented by a vector of constant length vo : =
2πr/(sidereal day)
directed always towards the east in the topocentric reference frame. Thus this
diurnal velocity vector has the following Cartesian components (in the
barycentric reference frame):
This vector is rotated back to J2000 by the precessional angle.
A short description of the FORTRAN code that generates both the position
and the velocity of a detector with respect to the SSB is given in
Appendix C.
|
VI. A LINEAR FILTER
The phase of the gravitational-wave signal contains terms arising from the
motion of the detector with respect to the SSB. These terms consist of two
contributions, one which comes from the motion of the Earth barycenter with
respect to the SSB, and the other which is due to the diurnal motion of the
detector with respect to the Earth barycenter. The first contribution has a
period of one year and thus for shorter observation times can be well
approximated by a few terms of the Taylor expansion. The second term has a
period of 1 sidereal day and to a very good accuracy can be approximated by a
circular motion. We thus propose the following approximate simple model
of the phase of the gravitational-wave signal:
|
Ψs(t) = p + p0t + |
s
Σ
k=1
|
pk tk+1 + A cos(Ωrt)
+ B sin(Ωrt), |
| (6.1) |
where Ωr is the rotational angular
velocity of the Earth. The parameters A and B can be related to the right
ascension α and the declination
δ of the gravitational-wave source through the
equations [cf. Eq. (18)
in Ref. [2]]
|
|
|
= |
|
ω0 r
c
|
cosδcos(α – φr), |
| (6.2a) | |
|
= | |
ω0 r
c
|
cosδsin(α – φr), |
| (6.2b) |
|
where ω0 is the angular frequency of the gravitational-wave signal and
r is defined in Eq. (5.3).
The phase model (6.1) has the property that it is a linear
function of the parameters. We have shown in Paper III that for linear phase
models the optimal statistics is a homogeneous random field and consequently
the statistical theory of signal detection described in
Sec. III of the
present paper applies to this case. The polynomial in time part of the phase
Ψs
[cf. Eq. (6.1)] contains two contributions.
The first one comes from
the intrinsic frequency drift of the gravitational waves emitted by a source.
For example, if the source is a spinning neutron star, the frequency of the
gravitational waves it emits can evolve as the frequency of the revolution of
the star. In general the star will lose its energy and will spin down. This
evolution of the frequency can be approximated by a Taylor series. The second
contribution comes from the Taylor expansion of the motion of the Earth around
the Sun. It is clear that the longer the observation time of the signal the
more terms of the Taylor expansion we need to include in order to accurately
approximate the true signal.
In order to verify the accuracy of the linear model
(6.1) we have calculated the fitting factor FF between
the linear model and the accurate model of the signal. As the
accurate model of the phase of the signal we have taken the following model:
|
Ψa(t) = Φ0 + ωdt + |
s+1
Σ
k=1
|
ωktk+1 + |
[ |
ω0 + |
s+1
Σ
k=1
|
(k + 1)ωktk |
] |
|
n0·rSSB(t)
c
|
, |
| (6.3) |
where ωd is the signal's frequency
ω0 shifted by a known
frequency ωs, i.e.
ωd = ω0
– ωs. The down-conversion frequency
ωs (as well as the bandwidth of
the signal) can be chosen arbitrarily and an appropriate time sequence can
be extracted from the frequency domain database as described in
Ref. [11]. The parameters
ωk
are spin-down parameters and they arise by approximating the intrinsic frequency evolution of the signal by a Taylor expansion. In the accurate
model (6.3) we include one more spin down than in
the linear model (6.1). This additional spin down
serves to represent the uncertainty of our model.
For the case when the signal is narrow-band around some frequency
ω0 the formula (3.15)
for the fitting factor can be approximated by
|
FF ≈ |
max
ζ
|
<cos[Ψa(t;ζa)
– Ψs(t;ζ)]>,
|
| (6.4) |
where
ζa =
(Φ0,ω0,ω1,…,ωs+1,α,δ)
are the parameters of the accurate model (6.3) and
ζ =
(p,p0,p1,…,ps,A,B)
are the parameters of the linear model (6.1). The linear
phase model (6.1) can shortly be written as
|
Ψs(t;ζ) = |
s+3
Σ
i=0
|
ζi li(t). |
| (6.5) |
The phase Ψa in the accurate model
(6.3) can be expressed as a sum similar to the sum
from Eq. (6.5) plus a certain remainder r that
we assume to be small:
|
Ψa(t;ζa)
= |
s+3
Σ
i=0
|
_
ζai |
(ζa) li(t) +
r(t;ζa). |
| (6.6) |
Note that the coefficients ζ‾ai
are some functions of the accurate phase parameters
ζa. In numerical calculations
described below the vector rSSB in the accurate phase
model (6.3) was computed by our Top2Bary
code described in Appendix C, and then the coefficients
ζ‾ai and the residual
r(t;ζa) were computed by making
a least-squares fit (within the observational interval) of the template
Σi ζ‾ai li(t)
to the accurate phase Ψa(t;ζa).
Making use of Eqs. (6.5) and
(6.6), from Eq. (6.4) one gets
|
|
|
max
ζ |
< | cos |
[ |
s+3
Σ
i=0 |
| ( |
_
ζai
|
– ζi |
) |
li(t) + r(t) | ] |
> |
|
|
|
|
max
ζ
|
<
| [ |
1 – |
1
2
|
|
s+3
Σ
i,j=0
|
| ( |
_
ζai
|
– ζi |
) |
| ( |
_
ζaj
|
– ζj |
) |
li(t) lj(t) |
] |
cos r(t)
|
|
|
|
|
| – |
s+3
Σ
i=0
|
( |
_
ζai
|
– ζi |
) |
li(t) sin r(t) | > |
,
|
| |
(6.7)
|
where the last approximation was obtained by Taylor expansion of the cosine
function and by keeping only the quadratic terms in the (assumed to be small)
differences ζ‾ai –
ζi. It is now easy to find in
Eq. (6.7)
the maximum over the parameters ζ as
the right-hand side of Eq. (6.7) is quadratic in
these parameters. The values of the parameters that maximize the fitting
factor are given by the solution of the following set of s + 4 linear equations:
|
|
s+3
Σ
j=0
|
Lij |  |
_
ζaj
|
– ζj |
 |
= –Li, |
| (6.8) |
where
|
|
|
: = |
<li(t) lj(t)
cos r(t)>, |
|
(6.9a) |
|
|
| (6.9b) |
|
We have used the above prescription to calculate the fitting factor numerically.
Once we have found the parameters of the extremum (6.7)
by solving Eqs. (6.8), we have used these values
as input to an optimization routine
(based on Nelder-Mead simplex algorithm) to find an accurate value of the
fitting factor directly from the formula (6.4) without the Taylor
expansion. Nelder-Mead method is one of algorithms to find extremum of a
function of n variables [13,14]. This algorithm involves
calculation of the function to be maximized at vertices of certain simplexes in
the parameter space but not function's derivatives.
In our calculation we have used the following estimates of the maximum values of
the spin-down parameters
where τmin is the minimum characteristic
spin-down age of the neutron star.
These estimates were adopted in the previous papers of this series and they
were taken from the work of Brady et al. [1].
We have computed the fitting factor for three phase models with s = 0, 1, 2,
i.e. for a monochromatic signal, 1-spindown signal, and 2-spindown signal.
We have carried out computations for two values of the spin-down age
(τmin = 40 years and
τmin = 1000 years), and for different
values of the signal's frequency f0 =
ω0/(2π)
and the observation time To. For each case we have
made calculation for a grid of positions of the source in the sky. We have
chosen our observations to start from the beginning of the year 2000
(Julian day = 2451545.0) and the position of the detector to coincide with
the geographical location of the EXPLORER resonant bar.
Our results are summarized in Tables I, II, and
III. For each grid of positions of the source in the sky we have
found the minimum value FFmin of the fitting factor (the worst
case). In the tables we have given the maximum length of the observation time
for which FFmin is greater than 0.9, 0.91/3, and 0.999.
The conservative value of the fitting factor equal to 0.91/3
~ 0.967
comes from the arguments of Apostolatos [10] by which such
a fitting factor leads to affordable 10% loss of events.
The ultraconservative value of the fitting factor equal to 0.999
gives a negligible loss of 0.3% of events.
From the results presented in Tables I, II, and III
it follows that the monochromatic linear model is adequate for a
few hours of the observation time, 1-spindown model for a few days of the
observation time, and 2-spindown model for around 1 week of the observation
time. For several months of the observation time we do not expect to fit an
adequate linear model however we know that for such long observation times a
coherent all-sky search is computationally prohibitive
[1,2].
Thus we conclude that in realistic (i.e. computationally feasible) coherent
searches of not more than 1 week duration a satisfactory linear model can be
chosen.
TABLE I. Adequacy of the monochromatic linear model.
| Frequency | Maximal observation time To (h)
|
| (Hz) | τmin = 40 years
| τmin = 1000 years
|
|
FFmin > 0.9 |
FFmin > 0.91/3 |
FFmin > 0.999 |
FFmin > 0.9 |
FFmin > 0.91/3 |
FFmin > 0.999 |
|
| 100 | 4 | 3 | 2 | 8 | 7 | 4 |
| 200 | 3 | 3 | 1 | 6 | 6 | 3 |
| 300 | 3 | 2 | 1 | 6 | 5 | 3 |
| 400 | 2 | 2 | 1 | 5 | 5 | 3 |
| 500 | 2 | 2 | 1 | 5 | 4 | 3 |
| 600 | 2 | 2 | 1 | 5 | 4 | 2 |
| 700 | 2 | 2 | 1 | 5 | 4 | 2 |
| 800 | 2 | 2 | 1 | 4 | 4 | 2 |
| 900 | 2 | 2 | 1 | 4 | 4 | 2 |
| 1000 | 2 | 2 | 1 | 4 | 4 | 2 |
|
TABLE II. Adequacy of the 1-spindown linear model.
| Frequency | Maximal observation time To (days)
|
| (Hz) | τmin = 40 years
| τmin = 1000 years
|
|
FFmin > 0.9 |
FFmin > 0.91/3 |
FFmin > 0.999 |
FFmin > 0.9 |
FFmin > 0.91/3 |
FFmin > 0.999 |
|
| 100 | 4 | 3 | 1 | 4 | 3 | 2 |
| 200 | 3 | 2 | 1 | 3 | 2 | 1 |
| 300 | 2 | 2 | 1 | 3 | 2 | 1 |
| 400 | 2 | 2 | 1 | 2 | 2 | 1 |
| 500 | 2 | 2 | 1 | 2 | 2 | 1 |
| 600 | 2 | 1 | 1 | 2 | 2 | 1 |
| 700 | 2 | 1 | 1 | 2 | 1 | 1 |
| 800 | 2 | 1 | 1 | 2 | 1 | 1 |
| 900 | 1 | 1 | 1 | 2 | 1 | 1 |
| 1000 | 1 | 1 | 1 | 2 | 1 | 1 |
|
TABLE III. Adequacy of the 2-spindown linear model.
| Frequency | Maximal observation time To (days)
|
| (Hz) | τmin = 40 years
| τmin = 1000 years
|
|
FFmin > 0.9 |
FFmin > 0.91/3 |
FFmin > 0.999 |
FFmin > 0.9 |
FFmin > 0.91/3 |
FFmin > 0.999 |
|
| 100 | 14 | 12 | 8 | 14 | 12 | 8 |
| 200 | 13 | 11 | 7 | 13 | 11 | 7 |
| 300 | 11 | 9 | 6 | 12 | 10 | 6 |
| 400 | 10 | 9 | 5 | 10 | 9 | 5 |
| 500 | 9 | 8 | 5 | 9 | 8 | 5 |
| 600 | 9 | 8 | 5 | 9 | 8 | 5 |
| 700 | 9 | 7 | 5 | 9 | 7 | 5 |
| 800 | 8 | 7 | 4 | 8 | 7 | 4 |
| 900 | 8 | 7 | 4 | 8 | 7 | 4 |
| 1000 | 8 | 7 | 4 | 8 | 7 | 4 |
|
|
VII. SPACING OF FILTERS, THE SEARCH ALGORITHM, AND
COMPUTATIONAL REQUIREMENTS
A. Grid of templates
In this section we shall present a construction of a grid in the parameter space
on which the statistics F will be calculated in order to search for signals.
We assume that as filter (or template) that we use in order to calculate the
statistics we shall use an approximations of the signal by a suitable linear
model studied in Sec. VI. We would like to choose the grid in such a
way that the additional loss of potential gravitational-wave signals due to the
finite spacing of the grid is negligible. In order to determine an appropriate
grid of templates we shall use the correlation function of the statistics F.
We shall choose the grid in such a way that the correlation function for two
filters evaluated for parameters at two neighboring points of the grid is not
less than a certain specified value.
This method is conceptually different from the approach that uses the Fisher
matrix as a metric on the parameter space. However when the Fisher matrix is
constant, i.e. independent of the values of the parameters, which is the case
for the linear model, the two approaches coincide. Metric approach is thus more
general than ours as it does not require constancy of the parameter-space
metric.
We consider here a constant amplitude signal
|
h(t;h0,Φ0,ξ)
= h0 sin[Φ(t;ξ) + Φ0], |
| (7.1) |
where Φ0 is the initial phase of
the wave form and the vector ξ collects
all other phase parameters.
The correlation function C of the optimum statistics F for signal
(7.1) can be approximated using Taylor expansion around
τ = 0. Keeping terms at most quadratic in
τi one gets
|
C(τ) ≈
1 – |
Σ
i,j
|
~
Γ
|
ij |
τi τj, |
| (7.2) |
| where the matrix |
~
Γ
|
has the components |
|
|
~
Γ
|
ij
|
: = |
∂Φ
∂τi
| |
∂Φ
∂τj
| |
– | |
∂Φ
∂τi
|
|
∂Φ
∂τj
|
| .
|
| (7.3) |
| The matrix |
~
Γ
|
is the reduced Fisher information matrix for |
the signal (7.1) where the initial phase parameter
Φ0 has been
reduced (see Sec. IV and Appendix B of Paper III for details).
The statistics F can be expressed as a Fourier transform where the parameter
p0 corresponds to angular frequency and consequently F can be calculated
using the FFT algorithm. However the FFT gives the values of the statistics on
a certain grid of frequencies called Fourier frequencies. These frequencies in
normalized units are separated by factor of 2π. Thus when the true
frequency falls between the two Fourier frequencies we cannot achieve the
theoretical maximum of the optimal statistics F. The worst case is when the
frequency falls half way between the Fourier frequencies. One can easily find
that in such a case the signal-to-noise ratio calculated approximately by means
of the Taylor expansion of the correlation function is equal only to 0.42 of the
optimal signal-to-noise ratio. This would lead to a drastic loss of signals.
Therefore we need a finer grid. A way to achieve this and still take advantage
of the speed of FFT is to pad the time series with zeros.7 Padding with zeros of
the length of the original time series gives a grid that is twice as fine as the
Fourier grid, i.e. the difference between the Fourier frequencies is equal
to π. Then in the worst case the signal-to-noise
ratio is 0.89 of the optimal
one. As we shall see later from Monte Carlo simulations this choice of spacing
of the frequencies leads to a search algorithm where there is no additional loss
of events due to bad grid spacing and the rms errors of the estimators of
parameters are close to the theoretical minimum. It is also useful to note that
the signal-to-noise ratio calculated form the exact correlation function formula
yields the values of the fractions of the optimal signal-to-nose ratio equal
to 0.63 and 0.90 for the difference between the Fourier frequencies equal to
2π and π,
respectively. This indicates the limits of the validity of the
Taylor expansion.
We introduce a convenient normalization of the spin-down parameters
pk of the linear model (6.1), namely
|
| _
pk
|
: = pk T | k+1
o | , k = 0, …, s. |
| (7.4) |
This is equivalent to using a time coordinate
t‾ : = t/To normalized
by the total observation time To (then the normalized time
duration of the signal is always 1). Using definition (7.4)
the linear phase model (6.1), after dropping the initial
phase parameter p, can be written as:
|
Φ(t;ξ)
= |
_
p0
|
t
To
|
+ |
s
Σ
k=1
|
|
_
pk
|
|  |
t
To
|  |
k+1
|
+ A cos(Ωrt)
+ B sin(Ωrt), |
| (7.5) |
where s is the number of spin downs included. In the quadratic approximation
(7.2) and for the phase model (7.5), equation
|
1 – |
Σ
i,j
|
|
~
Γ
|
ij |
τi τj = C0 = const, |
| (7.6) |
describes the surface of the (s + 3)-dimensional correlation hyperellipsoid.
It is clear that we cannot fill the parameter space completely with
hyperellipsoids. But such filling can be done by means of some prisms
constructed with the aid of the correlation hyperellipsoid. We shall illustrate
our construction in the special case of 1-spindown (i.e., s = 1) linear phase
model (7.5).
| In this case the components of the matrix |
~
Γ
|
as functions of the observation |
time are given by [here the order of the phase parameters is as follows:
|
|
~
Γ
|
= |  |
|  |
, |
| (7.7) |
where n is the observation time expressed in sidereal days, i.e.,
n : = (ΩrTo)/(2π).
In the first step we choose spacing in the frequency
parameter p‾0 to be equal to
π. Then we compute the
value C0 of the correlation at the surface of the 4-dimensional
correlation hyperellipsoid (7.6) by requesting that
the p‾0 axis
intersects this surface at the points
Δp‾0
= ±π/2.
Substituting τ
= (Δp‾0,0,0,0) into
Eq. (7.6), one gets
|
C0 = 1 –
|
~
Γ
|
|
Δ |
_
p
|
2
0 |
= 1 –
|
π2
48 |
≈ 0.79. |
| (7.8) |
Making use of Eqs. (7.7) and (7.8),
the general equation (7.6) can be written in the case of
1-spindown signal in the form
[we also substitute τ =
(p‾0,p‾1,A,B)]
|
A2 + B2 + |
1
6
|
|
_
p
|
2
0
|
+ |
1
3
|
|
_
p0
|
|
_
p1
|
+ |
8
45
|
|
_
p
|
2
1
|
+ 2ζ2A |
_
p1
|
– 2ζB( |
_
p0
|
+ |
_
p1
|
) – |
π2
24
|
= 0, |
| (7.9) |
where we have introduced
We first construct the elementary cell of the grid in the filter space
(which is the space spanned by the parameters p‾1, A, and B).
We consider the p‾0 = 0 cross section
of the 4-dimensional hyperellipsoid (7.9). This cross
section defines the 3-dimensional ellipsoid in the (p‾1,A,B) space:
|
(A + ζ2 |
_
p1
|
)2 +
(B – ζ |
_
p1
|
)2 = |
π2
24
|
– |  |
8
45
|
– ζ2 –
ζ4 |
 |
|
_
p
|
2
1
|
|
| (7.11) |
(let us note that 8/45 – ζ2 – ζ4 > 0 for
n ≥ 1).
Next we take the cross sections of the ellipsoid (7.11)
with the planes p‾1 =
±δ for some positive constant
δ. These cross
sections define two adjacent circles. We inscribe two regular hexagons into
these circles. The hexagons form the bases of the inclined prism inscribed in
the ellipsoid (7.11). The 3-dimensional volume of this prism reads
|
V(δ) = 3√3 |
[ |
π2
24
|
– |  |
8
45
|
– ζ2 – ζ4 |
 |
δ2 | ] |
δ. |
| (7.12) |
Then we maximize the volume V(δ) with respect to
δ. The function V(δ)
attains its maximal value for
The maximal value V(δmax) of the volume (7.12)
is the volume of the elementary cell in the filter space. It reads
Equation (7.14) gives the following values of the volume Vgr
of the elementary cell in the filter space:
Vgr=2.05, 1.35, 1.29, 1.27 for n = 1, 2, 3, 4, respectively.
The elementary cell in the 4-dimensional space
(p‾0,p‾1,A,B) we construct as follows. The
3-dimensional prism of maximal volume, described above, which lies in the
p‾0 = 0 subspace, we parallelly translate
in four dimensions, in two opposite directions, into the subspaces
p‾0 = –π/2
and p‾0 =
+π/2. As the direction of translation we choose
one of the principal directions8
of the hyperellipsoid (7.9). Such constructed elementary
cell is the 4-dimensional prism which bases are two adjacent 3-dimensional
hexagonal prisms lying in the p‾0
= –π/2 and p‾0
= +π/2 subspaces.
It is clear from the construction that our elementary cell will stick out the
4-dimensional hyperellipsoid (7.9). For the case of n = 2
we have calculated the correlation function
| C(τ) = 1
– Σi,j |
~
Γij
|
τiτj |
at all vertices of the elementary cell and we have found that the smallest
value of C(τ) is equal to 0.77. Thus the
grid constructed above ensures that the correlation between the filter and
the signal is not less than 0.77. The Monte Carlo simulations presented
below show that using such a grid we do not lose any signals and that rms
errors of the parameter estimators are very close to the minimum ones allowed
by the Cramèr-Rao bound.
If as a base of the elementary cell in the filter space we choose a square
instead of a regular hexagon the volume of the cell (independently of the value
of n) decreases by a factor of 3√3/4 ~ 1.3.
B. Monte Carlo simulations
In order to test the effectiveness of the chosen grid we have made Monte Carlo
simulations of the detection of our signal in the noise and estimation of its
parameters. In the simulations we have taken the signal s to be 1-spindown
linear model with a constant amplitude h0:
where To is the observation time and n is the integer equal to the number
of sidereal days of observation in real search. Simulation of parameter
estimation of the accurate signal with the phase given by Eq. (6.3)
are presented in the next subsection. In the case of signal (7.15) the
maximum likelihood detection involves finding the global maximum of the
functional Fs with respect to the parameters p0, p1, A, B. The
functional Fs is given by
where
|
|
~
X
|
= | ∫ |
To
0
|
x(t) exp | { |
–i | [ |
p1t2 + A cos |
 | 2πnt
To
|  |
+ B sin |  |
2πnt
To
|
 |
] | } |
exp(–ip0t) dt. |
| (7.17) |
In Eq. (7.17) the data x(t) = s(t) + n(t), where
n(t) is the stationary noise with spectral density Sh. In our
simulations we have generated white and Gaussian noise n(t). Thus our
statistics Fs consists of taking the modulus of the Fourier
transform of the data demodulated for a grid of parameters p1,
A, and B. To find the maximum of Fs we have used a
hierarchical algorithm consisting of two steps: a coarse search and
a fine search. The coarse search involves calculation of
Fs on the grid in the parameter space constructed in
Sec. VII A and finding the maximum
value of Fs on that grid. The values of the parameters of the filter that
give the maximum are coarse estimates of the parameters of the signal. The fine
search involves finding the maximum of Fs using a maximization routine with
the starting values of the parameters equal to the coarse estimates of the
parameters. As a maximization routine we have used the Nelder-Mead simplex
algorithm. We plan to use the above hierarchical procedure in analysis of real
data from the EXPLORER detector.
The procedure described above differs from another two-step hierarchical
algorithm proposed by Mohanty and Dhurandhar
[8,9]. The first step
of the two procedures is the same but in the second step Mohanty and Dhurandhar
propose to use a fine grid in the parameter space around the maximum obtained
from the coarse search whereas we propose to use a maximization routine.
However as any optimization routine the Nelder-Mead algorithm may fail to find
the global maximum. Therefore in the real data search we may have to use a
combination of both hierarchical procedures: whenever our maximization routine
fails we use as the second step a fine search proposed by Mohanty and
Dhurandhar.
We have performed Monte Carlo simulations by generating a signal s(t) given by
Eq. (7.15) and adding white Gaussian noise n(t). By adjusting the
amplitude h0 we have generated a signal with a chosen optimal signal-to-noise
ratio d. In our simulations we have chosen the observation time to be n
= 2. We have done 1000 runs for several values of d. We have compared
the standard deviations of the parameter estimators obtained from the
simulations with the theoretical ones calculated from the Cramèr-Rao
bound. We have also compared the probability of detection of the signal
obtained from the simulations with the theoretical one calculated from
Eq. (3.8). In our simulations we have used the
hexagonal grid constructed in
Sec. VII A.
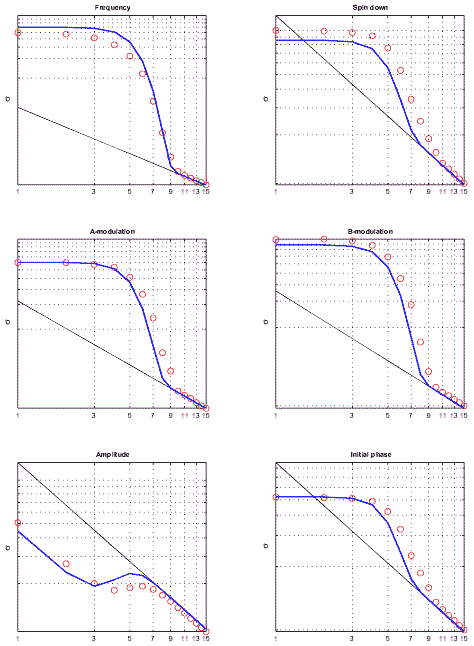
The results of our computations are depicted in Fig. 1. We have
observed that above a certain signal-to-noise ratio (that we shall call the
threshold signal-to-noise ratio) the results of the Monte Carlo
simulations
agree very well with the calculations of the rms errors from the covariance
matrix. However below the threshold signal-to-noise ratio they differ by a
large factor. This threshold effect is well-known in signal processing
[16] and has also been observed in numerical simulations for
the case of
a coalescing binary chirp signal [17,18].
As was explained in Sec. VII of Paper III this effect arises because
sometimes the global maximum of the
functional Fs occurs as a result of noise and not the signal.
This happens
the more often the lower the signal-to-noise ratio. Following the theory of
this effect developed in Paper III we have calculated the approximate rms errors
of the estimators of the parameters. They are shown as thick lines in Fig. 1.
The comparison of probability of detection obtained from the simulations with
the theoretical formula (3.8) shows that for lower signal-to-ratios we have
more detections than expected. This is because the theoretical formula assumes
that when the signal is detected its parameters are located in the cell
corresponding to the true parameters of the signal. However in practice for
lower values of d as a result of the noise the signal may drift to neighboring
cells. Thus for threshold signal-to-noise ratio of 7 we find that simulated
probability of detection is 5% greater than the theoretical one whereas for
signal-to-noise 8 and greater the simulated and the theoretical probabilities
of detection agree within 0.5%.
|
FIG. 1. Monte Carlo simulations of the rms errors of the parameter estimators
of the signal given by Eq. (7.15) for n = 2. The x axes
are labeled by the optimal signal-to-noise ratio d. The y axes are labeled by
the standard deviation σ except for the case of
the amplitude parameter where the relative rms error
σr :=
σ/h0 is given. Both
σ and σr
are dimensionless. The results of simulations of 1000 runs for
each value of d are marked by the circles. The thin solid lines are
calculated from covariance matrix and they constitute the Cramèr-Rao
bound, i.e. the smallest rms error for an unbiased estimator. The thick
solid lines are calculated from a model that takes into account the false
alarms. |
C. Estimation of parameters of the signal
Once the optimal statistics, calculated with the linear filter of
Sec. VI, crosses a chosen threshold we register
the estimates of the
parameters p0, p1, A, and B. We would like to
estimate physically
interesting parameters: frequency, spin down, declination and right ascension
of the source. We propose the following algorithm to achieve this. From
Eqs. (7.18) and least-squares fit of the linear model to the accurate
model of the signal we calculate the approximate values of parameters
ω0, ω1,
δ, α.
Then using the accurate model of the signal as a filter we search for
accurate estimates of the parameters on a
small grid around the approximate estimates.
We have made Monte Carlo simulations of the above procedure by making 100 runs
for one position of the source in the sky and for five signal-to-noise ratios:
8, 12, 16, 20, 24. First of all we have found that probability of detection of
the signal from simulation agrees within 0.5% with the theoretical one.
Concerning accuracy of the parameter estimation we have obtained
that rms errors for declination and right ascension were very close to their
Cramèr-Rao bounds, however the rms errors for frequency and spin down were
worse. The mean biases in the estimators of the parameters
ω0,
ω1,
δ, and α were less than
0.1%, 0.5%, 0.005%, and 0.01%, respectively.
D. Amplitude modulation
Approximation of the continuous gravitational-wave signal by a simple linear
model and consequently approximation of the optimal statistics F,
Eq. (3.3), by a homogeneous random field were studied under the assumption that
the amplitude of the signal was constant. However as the modulation of the
amplitude of the signal is very slow (it changes on a time scale of one sidereal
day) in comparison to the rapid modulation of the phase we expect that our
linear model of the phase is a satisfactory approximation of the phase of the
optimal filters given by Eqs. (3.4). We also expect that the calculation
of the number of elementary cells (except for a factor of 2, see below) and
construction of the grid in the parameter space given in Sec. VII A above are
valid for the amplitude modulated signal.
To calculate the optimal statistics F, we first need to correct
the time series for amplitude modulation i.e. multiply the time series by the
functions a(t) and b(t). Our grid is on the space parameterized by p0,
p1, A, and B whereas the functions a(t) and b(t) depend on the
declination δ and the right ascension
α. From Eqs. (6.2) we
have the following expressions for δ and
α in terms of A and
B:
Since for each set of parameters A and B there are two sets of parameters
δ and α
the number of cells needs to be multiplied by a factor of
2 and this number is to be used to compute from Eq. (3.5)
the threshold corresponding to a given false alarm probability.
We see that the declination δ
of the source, Eq. (7.18a), depends on
the angular frequency ω0
of the signal that we do not know before we detected the signal.
The uncertainty in δ affects the constant
amplitudes in front of the time dependent modulation factors. However for the
case of the EXPLORER detector data (which we plan to analyze employing the
methods developed above) we have that frequency
f0 is around 1 kHz within the
band B ~ 1 Hz
(see Sec. VIII).
Thus by choosing in the equation for declination δ
the frequency equal to the middle frequency of
the band to be analyzed instead of the unknown frequency
ω0, we shall
lose at most only a fraction ~
B/(2f0) ~ 0.0005 of the
signal-to-noise ratio.
E Computational requirements
To estimate the computational requirements to do the search we
calculate the number of FFTs that one needs to compute. This number depends on
the total volume VF of the filter space, which is given by
|
VF = | ∫ |
| ∫ |
B2(0,ro)
|
dA dB | ∫ |
ωmaxTo2/(2τmin)
–ω
maxTo2/(2tmin)
|
d |
_
p1
|
, |
| (7.19) |
where ωmax is the maximum angular frequency of the signal and
B2(0,ro) is a 2-dimensional disc in the (A,B) plane of radius ro,
Thus we get
|
VF = |
π
c2
|
|
ωmax3
r2To2
τmin
|
. |
| (7.21) |
The number of grid points on which the optimal statistics F, Eq. (3.3),
should be calculated is obtained by dividing the volume VF of the filter
space by the volume Vgr of the elementary cell of the chosen grid in
the filter space. In the previous subsection we have found that for each set
of parameters A and B there are two sets of parameters δ and α
[see Eqs. (7.18)]. Moreover the optimal statistics involves calculations
of two FFTs-Fa and Fb [see Eqs. (3.3) and (3.4)]. Thus
the total number NFFT of FFTs is 4 times the number of grid points
and it is given by
Assuming that the data processing rate should be comparable to the data
acquisition rate and that the data processing consists only of computing
the FFTs the number P of floating point operations per second
(flops) can be estimated by
|
P = 6ΔνN
FFT |
[ |
log2(2ΔνTo) + |
1
2
| ] |
, |
| (7.23) |
where Δν =
(ωmax – ωs)/(2π)
is the bandwidth of the
search. Equation (7.23) does not take into account the computational
requirements to do the fine search. This is because the fine search will only
be triggered when there is threshold crossing and this as estimated in the next
section will be a rare event. It is worth pointing out that the formula
(7.23) coincides with the analogous formula for a broadband search (see,
e.g., Ref. [1]) with the maximum frequency replaced by the bandwidth
of the search.
|
VIII. A NARROWBAND ALL-SKY SEARCH OF EXPLORER DATA
The data analysis tools for searching continuous gravitational-wave signals that
we have developed in the previous sections of the present work can be applied
both to the resonant bar and the laser interferometric detectors. We plan to
apply these tools to the data from the resonant bar detector
EXPLORER9 [19]. The
detector has already collected many years of data with high duty cycle (e.g. in
1991 the duty cycle was 75%). Our primary objective is to carry out an all-sky
search. It is a unique property of the gravitational-wave detectors that with a
single time series one can search for signals coming from all sky directions.
In the case of other instruments like optical and radio telescopes to cover the
whole or even part of the sky requires a large amount of expensive telescope
time. The directed search of the galactic center has already been carried out
and limits for the amplitude of the gravitational waves has been established
[20].
The EXPLORER detector is most sensitive over certain two narrow bandwidths
(called minus and plus modes) of about 1 Hz wide at two frequencies around
1 kHz. To make the search computationally feasible we propose an all-sky search
of data of a few days long in the narrow band were the detector has the best
sensitivity. By narrowing the bandwidth of the search we can shorten the length
of the data to be analyzed as we need to sample the data at only twice the
bandwidth and thus we reduce the computational time. To reduce the parameter
space to search we restrict ourselves to only one spin-down parameter. We would
also like to use the linear filter model as the search template. Then as our
frequency is around 1 kHz from Table II we read that we can consider
up to 2 days of coherent observation time in order that the fitting factor is
greater then 0.9. For the sake of the FFT algorithm it is best to keep the
length of the data to be a power of 2. Consequently we choose the number of
data points to analyze to be N = 218. Then for To = 2
days of observation time the bandwidth
Δν of the data will be
Δν =
N/(2To) ~ 0.76 Hz. We also choose
to analyze the data for the
plus mode which has frequency around 922 Hz. With these parameters we can
calculate the number of filters that we need to compute.
From Eq. (7.22) and for the hexagonal grid over the
sky we get that NFFT ~ 3.7×108. Assuming that the data processing rate
should be comparable to the data acquisition rate the computing power required
[calculated by means of Eq. (7.23)] is around 7.7 Gflops. If we allow
a month for off-line processing of data with the above parameters we only need
around 250 Mflops of computer power.
From Eq. (3.11) we can calculate the threshold that we
need to set. For example choosing the false alarm probability to be 1% we
find by inverting Eq. (3.11) and using Eq.
(3.10) that for the parameters that we have chosen above the
threshold signal-to-noise ratio is 8.3. However we know that in the coarse
search we are
using a suboptimal filter and we are losing signal-to-noise ratio. For the
parameters of our search we find that in the worst case the fitting factor is
0.94. Moreover due to our discrete grid in the parameter space the
signal-to-noise ratio can decrease in the worst case by an additional factor of
√(0.77) ~ 0.88. Thus in the worst case the signal-to-noise ratio of our
coarse search can be a factor of 0.83 of the optimal one. Hence in order not
to lose any signals we lower the signal-to-noise threshold by a factor of 0.83.
By lowering the threshold we must make sure that the number of false alarms does
not increase excessively. From Eq. (3.12) we find that the expected
number of false alarms with the lower threshold is
~ 310. This is
certainly a manageable number that will insignificantly increase the
computational time of the total search. We can consider lowering the threshold
even further in order to have more candidate events that can be later verified
using longer stretches of data. For example by lowering the threshold by a
factor of 0.8 the expected number of false alarms is around 1600 which will
still be manageable to verify.
The minimum detectable amplitude h0, i.e. the amplitude for which the
signal-to-noise ratio is equal to 1, is given by
where Sh is the one-sided spectral density of noise. For 2 days of
observation time To and spectral density Sh at the plus mode equal to
2×10–42/Hz, the minimum detectable amplitude is
3.4×10–24. In order that we have a detection with 99% confidence by
the calculation above we need a signal-to-noise ratio of 8.3 and thus the
amplitude of the signal must be around 2.8×10–23. Consequently by
estimate given in Eq. (2.3) a continuous gravitational-wave signal from a
neutron star located at a distance of 1 kpc, spinning with period of 2 ms, and
with ellipticity ε ~ 10–5 will be detectable.
|
ACKNOWLEDGMENTS
One of us (A.K) would like to thank ROG group in Istituto Nazionale di Fisica
Nucleare (INFN), Frascati, where part of this work was done, for hospitality
and Consiglio Nazionale delle Ricerche (CNR) for support within the exchange
agreement with Polish Academy of Sciences. This work was supported in part by
the KBN Grant No. 2 P03B 094 17 (K.M.B., P.J., and A.K.). We would also like
to thank Interdisciplinary Center for Mathematical and Computational Modeling of
Warsaw University for computing time.
|
APPENDIX A: BEAM-PATTERN FUNCTIONS
1. Interferometric beam-pattern functions
Noise-free response function h of the laser interferometric detector is
defined as the difference between the wave induced relative length changes of
the two interferometer arms. Derivation of formula (2.1)
in the case of the
laser interferometer can be found e.g. in Sec. II A
of Ref. [20].
Explicit formulas for the interferometric beam-pattern functions
F+ and F× from Eq. (2.1)
are derived e.g. in Sec. II A of
Ref. [2]. The functions read
|
|
|
sinζ[a(t) cos2ψ
+ b(t) sin2ψ], |
|
(A1a) | |
|
sinζ[b(t) cos2ψ –
a(t) sin2ψ], |
|
(A1b) |
|
where
|
|
|
|
|
1
4
|
sin2γ(1 + sin2φ) (1 + sin2δ)cos[2(α – φr –
Ωrt)] |
|
|
|
|
– |
1
2
|
cos2γsinφ(1
+ sin2δ)sin[2(α
– φr – Ωrt)] |
|
|
|
|
+ | 1
4
|
sin2γsin2φsin2δcos(α
– φr – Ωrt) |
|
|
|
|
|
– |
1
2
|
cos2γcosφsin2δsin(α – φr –
Ωrt) |
| |
|
|
(A2a) |
|
|
|
cos2γsinφsinδcos[2(α – φr –
Ωrt)] |
| |
|
|
+ |
1
2
|
sin2γ(1
+ sin2φ)
sinδsin[2(α –
φr – Ωrt)] |
| |
|
|
+ cos2γcosφcosδcos(α – φr –
Ωrt) |
|
|
|
|
| + |
1
2
|
sin2γ
sin2φcosδsin(α – φr
– Ωrt). |
| (A2b) |
|
In Eqs. (A1) ζ is the angle
between the interferometer arms (usually ζ = 90°)
and ψ is the polarization angle of the wave. In
Eqs. (A2) the angles α
and δ are respectively right
ascension and declination of the gravitational-wave source. The geodetic
latitude of the detector's site is denoted by φ
[its precise definition is given in Eq. (5.1a)],
the angle γ determines the orientation of
the detector's arms with respect to local geographical directions:
γ is
measured counter-clockwise from East to the bisector of the interferometer
arms. The rotational angular velocity of the Earth is denoted by
Ωr, and
φr is a deterministic phase which
defines the position of the Earth in its diurnal motion at t = 0 (the sum
φr +
Ωrt essentially coincides with
the local sidereal time of the detector's site, i.e. with the angle between the
local meridian and the vernal point; see
Sec. VII B).
2. Bar beam-pattern functions
We consider here the response of a bar detector to a weak plane gravitational
wave in the long wavelength approximation. Moreover, we assume that the
frequency spectrum of the gravitational wave which hits the bar entirely lies
within the sensitivity band of the detector. Under these assumptions the
dimensionless response function h of the bar detector can be computed from
the formula (cf. Sec. 9.5.2 in Ref. [21])
|
where n denotes the unit vector parallel to the symmetry axis of the
bar, | ~
H | is |
the three-dimensional matrix
of the spatial metric perturbation produced by the wave in the proper
reference frame of the detector,
and a dot stands for the standard scalar product in the three-dimensional
Cartesian space. In the detector's reference frame we introduce Cartesian
detector coordinates (xd,yd,zd) with the
zd axis along the Earth's radius pointing toward zenith, and the
xd axis along the bar's axis of symmetry. In these coordinates
the vector n from Eq. (A3) has components
In the wave Cartesian coordinate system
(xw,yw,zw) (in which the wave travels in the
+zw direction), the three-dimensional matrix H of the wave induced
spatial metric perturbation has components
|
H(t) = |  |
|  |
, |
| (A5) |
where the functions h+ and h× describe two independent wave's
polarizations. |
The matrices | ~
H | and H are related
through equation |
|
|
~
H
|
(t) = M(t) H(t) M(t)T, |
| (A6) |
where M is the three-dimensional orthogonal matrix of transformation from the
wave coordinates to the detector coordinates, T denotes matrix transposition.
Collecting Eqs. (A3)–(A6)
together one can see that the
response function h is a linear combination of the functions h+ and
h×:
|
h(t)=F+(t)h+(t) + F×(t)h×(t), |
| (A7) |
where F+ and F× are beam-pattern functions.
Because of the diurnal motion of the Earth the beam-patterns F+ and
F× are periodic functions of time with a period equal to one sidereal
day. We want to express F+ and F× as functions of the right
ascension α and the declination δ
of the gravitational-wave source and the polarization angle ψ
(the angles α, δ, and ψ
determine the orientation of the wave reference frame with respect to the
celestial reference frame defined below). We represent the matrix M of
Eq. (A6) as
where M1 is the matrix of transformation from wave to celestial frame
coordinates, M2 is the matrix of transformation from celestial coordinates to
cardinal coordinates and M3 is the matrix of transformation from cardinal
coordinates to detector coordinates. In celestial coordinates the z axis
coincides with the Earth's rotation axis and points toward the North pole, the
x and y axes lie in the Earth's equatorial plane, and the x axis points
toward the vernal point. In cardinal coordinates the (x,y) plane is tangent
to the surface of the Earth at detector's location with x axis in the
North-South direction and y axis in the West-East direction, the z cardinal
axis is along the Earth's radius pointing toward zenith. Under the above
conventions the matrices M1, M2, and M3
are as follows (matrices M1
and M2 are taken from Sec. II A of
Ref. [2])
|
|
= |
 |
|  |
, |
| (A9a) |
|
|
= |
 |
|  |
, |
| (A9b) |
|
|
= |
|
 |
|
 |
. |
|
(A9c) |
|
In Eq. (A9b) φ is
the geodetic latitude of the detector's site,
Ωr is the rotational angular velocity
of the Earth, and the phase φr
defines the position of the Earth in its diurnal motion at t = 0 (the
sum φr +
Ωrt essentially coincides with
the local sidereal time of the detector's site;
see Sec. V B)
in the present paper. In Eq. (A9c)
γ determines the orientation of the bar's axis
of symmetry with respect to local geographical directions, it is measured
counter-clockwise from East to the bar's axis of symmetry.
To find the explicit formula for F+ and F×
we have to combine
Eqs. (A3)–(A9).
After some algebraic manipulations we arrive at the expressions:
where
|
|
|
|
|
1
2
|
(cos2γ –
sin2γsin2φ)(1
+ sin2δ)cos[2(α – φr – Ωrt)] |
| |
|
|
+ |
1
2
|
sin2γsinφ(1
+ sin2δ)sin[2(α
– φr – Ωrt)] |
| |
|
|
– |
1
2
|
sin2γsin2φsin2δcos[α – φr
– Ωrt] |
| |
|
|
+ |
1
2
|
sin2γcosφsin2δsin(α – φr – Ωrt)
|
| |
|
|
+ |
1
2
|
(1– 3sin2γcos2φ)cos2δ, |
| (A11a) |
|
|
|
–sin2γsinφsinδcos[2(α
– φr – Ωrt)] |
|
|
|
|
+ (cos2γ –
sin2γsin2φ) sinδsin[2(α –
φr – Ωrt)] |
|
|
|
|
– sin2γcosφcosδcos(α – φr – Ωrt) |
|
|
|
| –
sin2γsin2φcosδsin(α –
φr – Ωrt). | | (A11b) |
|
In Eqs. (A10) and (A11)
α, δ,
ψ, φ,
Ωr, and
φr all have the same meaning as in
Eqs. (A1)–(A2); the angle
γ determines the orientation of the bar detector
with respect to local geographical directions: γ
is measured counter-clockwise from East to the bar's axis of symmetry.
Equivalent explicit formulas for the functions a and b from
Eqs. (A11) can be found in
Ref. [22] where different
angles describing the position of the gravitational-wave source in the sky
and the orientation of the detector on the Earth are
used.10
APPENDIX B: THE TIME AVERAGES <a2>
and <b2>
1. Laser interferometeric detector
The time averages
<a2> and
<b2>
entering Eqs. (3.1), for
the observation time To chosen as an integer number of sidereal days, for the
laser interferometeric detector take the form (here n is a positive integer):
|
|
|
|
| 1
16
|
sin22γ | [ |
9cos4φcos4δ + |
1
2
|
sin22φsin22δ |
|
|
|
|
|
| + |
1
32
|
(3 – cos2φ)2(3 –
cos2δ)2 |
] |
|
|
|
|
|
|
+ | 1
32
|
cos22γ[4cos2φsin22δ
+ sin2φ(3 –
cos2δ)2], | |
(B1a) |
|
|
|
|
|
1
32
|
sin22γ[(3 –
cos2φ)2sin2δ
+ 4sin22φcos2δ]
|
| |
|
|
| + |
1
4
|
cos22γ(1 + cos2φcos2δ).
|
| (B1b) |
|
We see that <a2>
and <b2>
depend only on one unknown parameter of the signal-the declination
δ of the gravitational-wave source. They
also depend on the latitude φ of the detector's
location and the orientation γ of the detector's
arms with respect to local geographical directions.
2. Resonant bar detector
For the resonant bar detector the time averages
<a2> and
<b2>, for
the observation time To being an integer number of sidereal
days, have the form:
|
|
|
|
| 1
4
|
(1 – 3sin2γcos2φ)2
cos4δ |
|
|
|
|
+ | 1
2
|
sin2γcos2φ(1 –
sin2γcos2φ)sin22δ
|
| |
|
|
|
+ | 1
8
|
[sin22γsin2φ
+ (cos2γ –
sin2γsin2φ)2](1
+ sin2δ)2, |
|
(B2a) |
|
|
|
|
1
2
|
(sin22γcos2φ
+ sin4γsin22φ) cos2δ
|
| |
|
|
| + |
1
2
|
( |
cos4γ + |
1
2
|
sin22γsin2φ
+ sin4γsin4φ |
) |
sin2δ. |
| (B2b) |
|
As in the case of the laser interferometeric detector, the time averages
<a2> and
<b2> depend on
the declination δ of the
gravitational-wave source, the latitude φ of
the detector's location, and the orientation γ
of the detector's axis of symmetry with respect to local geographical directions.
APPENDIX C: THE Top2Bary PROCEDURE
The algorithms described in Sec. V were implemented in an easily callable
subroutine named Top2Bary consisting of about 900 lines of FORTRAN code.
The ephemeris files (DE405'90.'10, tai-utc.dat and yearly
eopc04.yy) required by the program must be kept in the directory
\Top2Bary\EphData on the current disk. The procedure header is shown
below.
subroutine Top2Bary(CJD_E,clat,clong,height,pve,pvo)
c Procedure to calculate position (km) and velocity (km/s) of an observatory
c located at given geographical position (conventional coordinates in degrees
c and height above the Earth ellipsoid in m) at given Julian day.
c It requires some ephemeris files, placed in the 'path' directory.
c Argument description:
c CJD_E - Julian Day number representing the Coordinated Universal Time
c If CJD_E is negative it is assumed that it is -1*(Ephemeris JD).
c clat - observatory conventional geographical latitude (deg).
c clong - observatory conventional geographical longitude (deg).
c height- observatory height above the Earth ellipsoid (m).
c pvo - 6 element array of barycentric vectors (3 for position in km, and
c 3 for velocity in km/s) of the observatory relative to Earth baryc.
c pve - 6 element array of barycentric vectors (3 for position in km,
c and 3 for velocity in km/s) of the Earth barycenter relative to SSB.
c More important subroutines called:
c polmot(CJD,Px,Py,UT1_UTC,dpsi,deps) - reads polar motion and UT1 data
c topobs(DJ1,glat,glong,height,pvo,amst) - returns observer's coord. in 'pvo'
c earthPV(BJD,pve) - returns Earth barycentric position (J2000 frame) in 'pve'
|
|
References
[1]
P. R. Brady, T. Creighton, C. Cutler, and B. F. Schutz,
Phys. Rev. D 57, 2101 (1998).
[2]
P. Jaranowski, A. Królak, and B. F. Schutz,
Phys. Rev. D 58, 063001 (1998).
[3]
M. A. Papa, P. Astone, S. Frasca, and B. F. Schutz,
in Proceedings of the 2nd Workshop on Gravitational Wave Data Analysis,
edited by M. Davier and P. Hello
(Éditions Frontièrs, 1998),
pp. 241-246.
[4]
M. A. Papa and B. F. Schutz,
in Proceedings of the XXXIVth Rencontres de moriond:
Gravitational Waves and Experimental Relativity,
edited by J. Trân Thanh Vân, J. Dumarchez, S. Reynaud, C. Salomon,
S. Thorsett, and J.-Y. Vinet
(World Publishers, Hanoi, 2000),
pp. 199-205.
[5]
P. R. Brady and T. Creighton,
Phys. Rev. D 61, 082001 (2000).
[6]
P. Jaranowski and A. Królak,
Phys. Rev. D 61, 062001 (2000).
[7]
B. J. Owen,
Phys. Rev. D 53, 6749 (1996).
[8]
S. D. Mohanty and S. V. Dhurandhar,
Phys. Rev. D 54, 7108 (1996).
[9]
S. D. Mohanty,
Phys. Rev. D 57, 630 (1998).
[10]
T. A. Apostolatos,
Phys. Rev. D 52, 605 (1995).
[11]
P. Astone et al.,
Phys. Rev. D 65, 022001 (2002).
[12]
E. M. Standish,
JPL Planetary and Lunar Ephemerides, DE405/LE405,
IOM 312.F-98-048 (1998).
[13]
S. Brandt,
Statistical and Computational Methods in Data Analysis
(Springer Verlag, New York, 1997).
[14]
J. C. Lagarias, J. A. Reeds, M. H. Wright, and P. E. Wright,
SIAM Journal of Optimization 9, 112 (1998).
[15]
J. Middleditch, W. Deich, and S. Kulkarni,
in Isolated Pulsars: Proceedings of the Los Alamos Workshop, held in Taos,
New Mexico, February 23-28, 1991,
edited by C. Ho, R. Epstein, and K. A. Van Riper
(Cambridge University Press, Cambridge, 1993).
[16]
H. L. Van Trees,
Detection, Estimation and Modulation Theory, Part I
(Wiley, New York, 1969).
[17]
K. D. Kokkotas, A. Królak, and G. Tsegas,
Class. Quantum Grav. 11, 1901 (1994).
[18]
R. Balasubramanian, B. S. Sathyaprakash, and S. V. Dhurandhar,
Phys. Rev. D 53, 3033 (1996).
[19]
P. Astone et al.,
Phys. Rev. D 47, 362 (1993).
[20]
P. Jaranowski and A. Królak,
Phys. Rev. D 48, 1723 (1994).
[21]
K. S. Thorne,
in Three Hundred Years of Gravitation,
edited by S. W. Hawking and W. Israel
(Cambridge University Press, Cambridge, 1987),
pp. 330-458.
[22]
M. Montero,
Ph. D. thesis,
Universitat de Barcelona, 1998.
|
Footnotes:
1F is the
log likelihood function Λ
with amplitudes Ai replaced by their ML
estimators Âi.
2For the
narrow-band signals considered in our paper the scalar product
(h|h') can
be approximated as
| (h|h') ≈
[2/Sh(f0)]∫ | To
0
| h(t) h'(t) dt. |
3The time
steps are available in the form of a table; see
hpiers.obspm.fr/webiers/general/earthor/utc/table1.html.
4They are
available as eopc04.yy files, where yy stands for
a two digit year number (e.g. 99 for 1999, and
00 for 2000); see
hpiers.obspm.fr/iers/eop/eopc04.
5For
past years, since 1962, the data necessary for
reduction are included in eopc04.yy files mentioned in footnote
4.
6It is
available via the Internet (anonymous ftp:
navigator.jpl.nasa.gov, the directory:
ephem/export) or on CD (from the publisher: Willmann-Bell, Inc.;
www.willbell.com/software/jpl.htm).
7Padding time
series with zeros of the length of the original time series in real signal
search means that we would need to calculate FFTs of twice the length of the
original data. This means doubling the computational time and the computer
memory used. To avoid this pulsar astronomers have invented special
interpolation algorithms that work in the Fourier domain and give twice as fine
Fourier grid from the FFT of the original data. In the analysis of EXPLORER
data we shall use one such algorithm provided to us by Duncan Lorimer (the
details of which can be found in Ref. [15]).
8The reasonable result one obtains only when
translating along this principal direction of the hyperellipsoid (7.9),
which almost coincides with the p‾0 axis.
9The EXPLORER detector is operated by the ROG collaboration
located in Italian Istituto Nazionale di Fisica Nucleare (INFN); see
www.roma1.infn.it/rog/explorer/explorer.html.
10Our functions
a and b from Eqs. (A11) are identical with the
functions S+ and S× from Eqs. (2.90) and (2.91) of
Ref. [22], provided the following identification
of the variables η, α, θ, Ψ used in [22]
with our variables Ωr, φr, α,
δ, φ, γ is made: η → –
(α – φr – Ωrt),
α → π/2 – δ,
θ → π/2 – φ,
Ψ → γ – π/2.
File translated from
TEX
by
TTH,
version 3.13 on 16 Oct 2002.