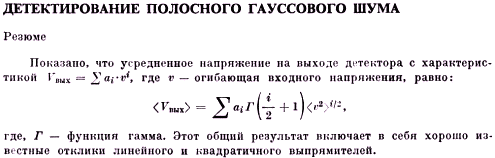
SCIENTIFIC INSTRUMENTATION
Nauch. apparat., 1987, 2, 1, 121-123 PL ISSN 0257-3881



DETECTING THE BAND-LIMITED GAUSSIAN NOISE

K. M. BORKOWSKI

Toruń Radio Astronomy Observatory,
Nicolaus Copernicus University
ul. Chopina 12/18, 87-100 Toruń, Poland


Simple formulae relating the mean output voltage of various detectors to the input noise power are developed.


The Gaussian noise, called also normal noise, is a common kind of signals met in various branches of science and technology. Its narrow band measurements are used as means to study a wide range of physical processes. Extreme exmples, where the noise power is the quantity of profound interest, include almost all radio astronomy observations and some experiments in thermometry.

The noise waveform itself may be consi ered as highly irregular voltage fluctuations around the zero level. Its power, apart of proportionality constant, is the time average of the squared voltage, or of squared instantaneous amplitude (the envelope): <v2>. In order to measure this quantity the signal, besides amplifying, is initially being frequency limited by passing it through a filter, and then rectified by means of a detector. The band limited noise has well known amplitude distribution of the form [1]

p(v) =  2
<v2>
exp–  v2
<v2>
,
 (1)

which is the Rayleigh distribution. The detector is always a nonlinear device whose averaged unidirectional output voltage or current is taken as a certain measure of the signal power at the input. In majority of noise measuring apparatus a voltage squaring rectifier is used as the detector. Obviously, the mean output voltage of this detector represents just the power of the input signal, <v2>. For reasons of this simplicity it became almost a custom to presume the square-law detector while analysing signal processing performed with the use of diverse variety of devices [2–4]. Another noise detector often used in practical applications is the linear one [5]. It is known to produce an averaged output equal to (π<v2>)1/2/2 [1].

The real detectors, however, rarely meet the requirement of perfect linearity or squareness which significantly restricts usefulness of the two, beautiful as they are, responses presented above. Since, in literature at hand, we have not found any generalization as to the expected output of a detector having arbitrary characteristics and fed with the Gaussian noise, we set out to derive some useful relationships relevant to the subject.

Consider first the general case of power-law detectors whose output voltage envelope is given by V = vn, where n is an integer greater than 0. The probability of finding the output between V and V + dV is the same as of finding the input between v and v + dv, so that p(V) dV = p(v) dv. Thus, it also follows that


<V> = ∞
∫
0
 V p(V) dV = ∞
∫
0
 vn p(v) dv = Γ( n
2
 + 1) <v2>n/2,
(2)

where Γ is the Euler gamma function and [6]:
Γ(  n
2
 + 1)  =  

 
(n/2)!,

n!
√
π
/{[(n – 1)/2]! 2n}, 

for even n,




for odd n.

(3)
 

Now, substituting in (2) for n the values of 2 or 1 we arrive immediately at the two particular solutions for the square-law and linear detector, respectively. The convenience of the power-law response as expressed by eq. (2) has been demonstrated elsewhere [7–10] through successful application to the analysis of the famous switched receiver [l1–14] and to radio interferometry.

Further extension of our results to other types of detectors may come out to be straightforward. For instance, the action of a quite general class of detectors can satisfactorily be expressed by a power sum (or series)

V = Σaivi,
 (4)

where the coefficients and index have their usual meaning. Averaging V in the manner of eq. (2) yields
<V> = ΣaiΓ(i
2		   + 1) <v2>i/2,
 
 (5)

which being simple is also general enough to satisfy the needs of many of potentially interested investigators.



   REFERENCES

  1.  BRACEWELL R. N ., The Fourier Transform and Its Applications, McGraw-Hill, New York 1965.
  2. KRAUS J. D., Radio Astronomy, McGraw.Hill, New York 1966.
  3. BENDAT J. S., PIERSOL A. G., Random Data: Analysis and Measurement Procedures, Wiley-Interscience, New York 1971.
  4. PENFIELD H., Multichannel filter Spectrometers, Meth. Exper. Phys., 12B, 266 (1976).
  5. EVANS J. V., in Radar Astronomy, Evans J. V. and Hagfors T. (eds.), McGraw.Hill, New York 1968, p. 499.
  6. DWIGHT H. B., Tables of Integrals and Other Mathematical Data, McMillan, New York 1961.
  7. BORKOWSKI K. M., Odbiorniki radioastronomiczne, Post. Astron., 28, 15 (1980).
  8. BORKOWSKI K. M., Analiza charakterystyk wzmocnienia odbiornika przełączanego, Post. Astron., 28, 315 (1980).
  9. BORKOWSKI K. M., Teoria odbioru interferometrycznego w radioastronomii, Post. Astron., 28, 79 (1980).
10. BORKOWSKI K. M., The Quiet Sun Brightness Temperature at 127 MHz, Solar Phys., 81, 207 (1982).
11. DICKE R. H., The Measurements of Thermal Radiation at Microwave Frequencies, Rev. Sci. Instrum., 17, 268 (1946).
12. ROBINSON B. J., Receivers for Cosmic Radio Waves, Ann. Rev. Astron. Astrophys., 2, 401 (1964).
13. TIURI M. E., Radio Astronomy Receivers, IEEE Trans. Military Electron., 8, 264 (1964).
14. PRICE R. M., Radiometer Fundamentals, Meth. Exper. Phys., 12B, 201 (1976).




File translated from TEX by TTH, version 3.13 on 24 Sep 2002.