K.M. Borkowski, Centre
for Astronomy, Nicolaus Copernicus University, Toruń, Poland
|
OptiCass program designed specifically to analyse the classical Cassegrain (CC) radio telescopes has recently been adapted for the case of the Ritchey-Chretien (RC) type telescopes which are known to perform much better than the classical Cassegrain in optical domain in that they practically eliminate the coma aberration thus allowing for wide field of views. With the help of this upgraded software it was found that the RC does perform better than CC also in radio domain but the improvements are relatively small. Some may be tempted to ascribe this to limitations of implementation of the ray tracing technique in this program. To dispell such doubts OptiCass was slightly modified so as to be able to work with and display very high frequencies, beyond radio range. Already at wavelengths of the order of 0.00001 m or 10 µm (30 THz) coma structure well known in optical telescopes is very nicely reproduced with OptiCass. Its RC variety (OptiCassRC) demonstrated very efficient removal of this aberration in the RC design. This report presents a few examples of comas obtained with OptiCass and compares them with optical counterparts taken from literature. The comparisons speak in favour of OptiCass, which originally wasn't intended to simulate telescopes at such high frequencies, so that it was strained close to its limits to do the presented job. |
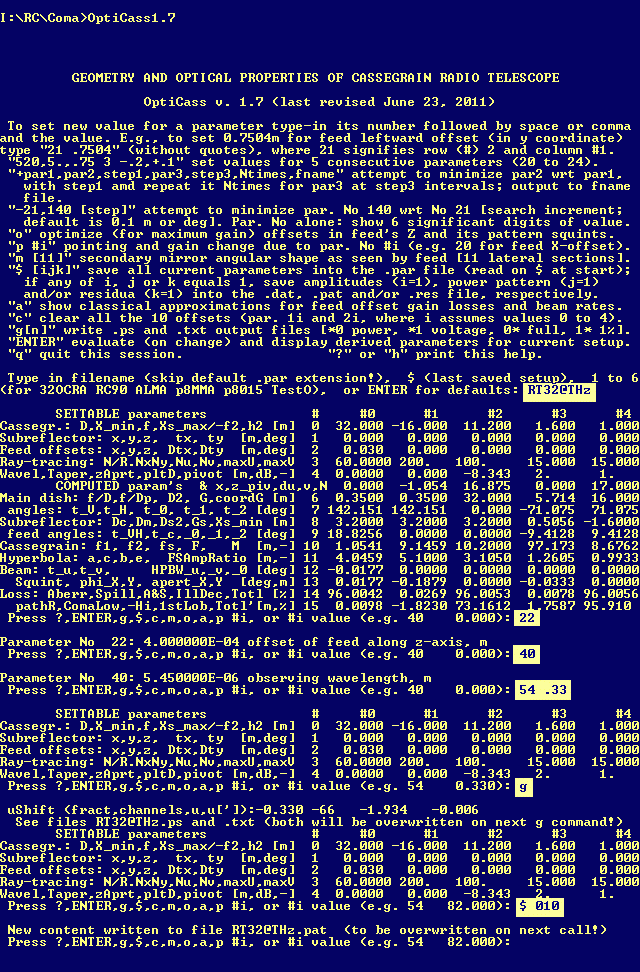
Two Cassegrain telescope designs were considered. Their main geometrical
characteristics are given in Tab. 1. and Fig. 1. which is the content
of screen displayed by OptiCass right from its initialization. Using these data
the reader may himself easily obtain all the results presented here as well as
experiment with other telescopes. To exactly reproduce our results for 32 metre
telescope just download the program executable
and parameter file, then run the program (you may drag
and drop the .par file onto the executable and wait a while) and on
prompts enter the inputs shown on the whitened background in Fig. 1.
In doing so be patient, because these are extreme settings (11 401
rays traced and (200+1)(100+1) = 20 301 points in the plotted power
spectra) and therefore, using a 2 GHz machine, it takes
the program several minutes to compute the telescope pattern.
Table 1: Design data of two
classical Cassegrains considered in this report
Aperture diameter, D 32.00 90.00 m Focal length of primary mirror, f 11.20 31.50 m Focal ratio of primary mirror, f/D 0.35 0.35 Subreflector diameter, d 3.20 9.00 m Height of secondary focus above primary vertex, h2 1.00 1.00 m Effective focal length, F 97.17 291.31 m Effective focal ratio, F/D 3.04 3.24 |
| Fig. 1: Initial setting and running of OptiCass program for analysis of 32-metre telescope of Tab. 1. at very high frequencies. Note the two very small values of parameters No 22 and 40, which are displayed in the main table rounded to zero. If needed, one enters them by hand the usual way (e.g. 22 4e-4 for the feed z-offset). Note also the excessive aberration losses (displayed as the number 96.0042 %) being due to phase errors at this feed offset and wavelength. |
The parameter No 41 (row 4, column #1)
in the first table of Fig. 1. is seen to be set to 0 which
means that the illumination function of this telescope is UNIFORM. This is
intentional for our present purpose is to simulate the optical telescope.
Users of previous versions of OptiCass will note a new program option activated by entering "54 value." This is usual way of ascribing a value to parameter No 54, but here value, if fractional, tells OptiCass to shift the pattern leftward by value (a fraction) of the spectral window width in u coordinate. This option was devised ad hoc for the sole purpose of having more 'economical' use of limited resolution of the final spectrum. The standard output, in which the main peak is centred in the window, would have most of its left half empty (flat) and to display the coma tail of Fig. 2. would require considerable widening of the available window, what means lowering of the resolution. Being ad hoc, the option does not behave as expected in all circumstances (in fact it spoils some measurements, notably the Aberr, parameter No 140, i.e. the aberration loss), so the reader should use it with utmost care.
| Fig. 2: Here is part of the output figure (RT32@THz.ps file) obtained with the setup of Fig. 1. after issuing this new command: 54 0.33 (to shift the pattern; see text) followed by g (graph command). |
Raw data used for production of the graphic file, like that in Fig. 2., can
be output to a .pat file with the command "$ 010" (without
quotation marks) and further processed. Below, in Fig. 3., is the result
of processing of such data with the help of a freeware program
QuikGrid (v. 5.4).
| Fig. 3: (Left panel) Contour map of power pattern (same as in Fig. 2.) of 32 m telescope at 55 THz and at optimal placement of feed at 3 cm off axis obtained with OptiCass, and (right panel) theoretical structure of coma (Φ = 6.4 λ ρ3 cosθ, where ρ is the normalized radial distance on the aperture and θ – the angular coordinate there) taken from Fig. 9.7. in Principles of Optics (Born & Wolf, 1980), after R. Kingslake, Proc. Phys. Soc., 61 (1948), 147. |
Excellent agreement of the two coma structures of the above figure,
one simulated in the OptiCass and the other predicted theoretically,
adds richly to the positive outcome of
other checks of the ray tracing method
as implemented in OptiCass. The next examples (Fig. 4.), where maps of
telescope radiation pattern are placed parallelly with actual images
of optical coma, are just further confirmation of this conclusion.
|
Estimating the coma size Although most of the coma energy is contained within so called sagittal coma (where opticians say reside about 80% of total power), which covers the V-shaped area from the tip up to the bottom of circular arc shown in the right part of Fig. 3., the overall angular extent of coma (including the whole outer circle) is three times greater than this (see for example Sacek, where similar relation is given for focal plane images):Λ = 3(xfeed/F)[D/(4F)]2 [rad], where xfeed is the feed lateral offset, F – the effective (or Cassegrain) focal length, and D – the main mirror diameter. Approximating the half-power beamwidth (HPBW) by 1.22λ/D and expressing the above angle in units of HPBW we getΛ = 3xfeed/(20λ) (D/F)3. Now we can check when coma should begin to be visible in power patterns of quite typical radio telescopes of Tab. 1. Since the minimum between the first sidelobe and main beam for circular apertures is at about 1.25 HPBW and the main beam is somewhat shifted into the coma, we may take for the condition of visibility of coma Λ > 1.5, i.e. 3xfeed/(20λ) (D/F)3 > 1.5 orxfeed > 10λ (F/D)3, which is 280λ for 32-m telescope and 340λ for 90-m telescope. These numbers tell us that at the wavelength λ = 1 cm (30 GHz) the feed offset should exceed about 3 m for the coma to only begin to manifest in the first minimum or sidelobe of directional pattern of typical radio telescope. Since feeds do not radiate uniformly, there is considerable tapering of illumination at the aperture edges. This means that the outer part of radio coma is considerably diminished in intensity, compared to examples presented in this report. Therefore, normally it is not clearly discernible.Conversely, with the feed offset fixed at 20 cm, the coma should show up at λ smaller than 20cm/280 = 0.071 cm and 20cm/340 = 0.059 cm for 32-m and 90-m antenna, respectively. This is above some 500 GHz in frequency for both the telescopes. Nevertheless, it should be born in mind that, although usually completely hidden under the main beam, coma leads to not insignificant signal loss also at lower frequencies, as demonstrated in this accompanying report on performance of a radio telescope with Ritchey-Chretien (hyperboloidal) mirrors. |
|
Fig. 4:
(Top panel) Images in focal plane in the presence of coma
Φ = C λ ρ3
cosθ, where C assumes values 0.3, 1, 2.4 , 5 and 10
(respectively, left to right); picture taken from Fig. 9.8. in Principles
of Optics (Born & Wolf, 1980), after K. Nienhuis, Thesis, University
of Groningen, 1948, p. 40. (Bottom panels) Contour maps of power pattern of 90 m Cassegrain telescope with lateral feed offset of 20 cm at 1, 3, 7.5, 15 and 30 THz, respectively (left to right). Each of the lower panels was computed in the same spectral window (15 spatial cycles on a side), thus they are gradually smaller when expressed as angles on the sky (from 10.3 to 0.34 arcsec, left to right). |
Fig. 5: Directional pattern of 90-m antenna at 30 THz and feed offset of 5 cm. |
The last figure, Fig. 6., shows how the power pattern of 90-metre antenna changes as we go down to practical frequencies, from 1 THz to 10 GHz. The 1 THz pattern image is just another presentation of leftmost coma at the bottom of Fig. 4. The feed offset was here kept constant at 200 mm in x and 6.27 mm in z. As the residual pattern (difference of the pattern in top part and one that is offset-free) reveals, the coma preserves about the same shape and changes essentially only in amplitude, becoming insignificant at longer wavelengths. Tab. 2. contains details about the three cases.
| Fig. 6: Power pattern of 90-m antenna at 1 THz, 100 GHz and 10 GHz, from left to right respectively. Comatic pattern distortions relative to the pattern of the same telescope with feed placed in the focus are shown in bottom panels, their amplitudes are here normalized (absolute values are given numerically in Tab. 2. in percent of the main beam). |
Table 2: Performance of 90-m telescope
at four frequencies
computed for uniform illumination (see also Fig. 6.)
Frequency 10 THz 1 THz 100 GHz 10 GHz Aberration loss [%] 96.020 19.136 0.211 0.002 Coma at maximum [%] 69.174 9.900 0.663 0.091 Side lobe height [%] 19.974 10.519 2.638 2.093 HPBW (max) ["] 0.191 0.735 7.048 70.451 Beam offset [deg] -0.039 -0.039 -0.039 -0.039 |