See also subsequent analyses.
RT32 Pointing Model
The RT32 telescope, due to its rigid construction, is quite
accurate an instrument that allows for precise pointing to a desired sky object at
most of observing frequencies. However, small deviations from an ideal case
in mechanical construction and electrical properties become gradually more important as higher frequencies are used. To be able to quickly and
unfailingly aim the telescope at any sky object, a steering system
must be given a model that accounts for all the inaccuracies down to
certain limit. Such a model is used to compute corrections to 'true'
sky coordinates (corresponding to an ideal construction) to obtain
'apparent' coordinates.
Here we describe a model worked out for the RT32 telescope based on
the standard pointing model used in the
Field System
(FS) and detailed in the Mark IV Field System Documentation,
Pointing Model
(Version 8.2/Sept. 1, 1993). The FS model, which is applicable
to a variety of telescope mounts (Toruń Alt-Az mount inclusive),
is based in turn on the model used to analyze Apollo 13 tracking data
(Apollo 13 MSFN Metric Tracking Performance, Final Report, Document
X-832-70-156, NASA GSFC, Greenbelt, July 1970).
The model implemented in the FS is approximate one. The approximations
are very good indeed. Still they necessarily fail in close proximity of
the zenith, which is not really a big problem, since this region is
practically inaccesible due to a blind spot caused by a singularity
at the zenith itself (where the azimith velocity corresponding to
diurnal motion is infinite and the zenith coordinate indeterminate).
Nevertheless, it is useful to have an exact model at least
to be able to check on accuracy of the approximated model. The general
exact model presented in the FS documentation is quite involved and is
based on vector and matrix calculus. We have derived an exact
altitude-azimuth model basing on spherical trigonometry solutions alone,
which turns out to be simple enough
to be directly implemented in a fitting process. Tests have proved that
the approximation model can be safely used in place of the exact one, at
least in the case of the RT32 telescope, whose parameters are very small.
When comparing our model with the FS model one should remember that
our definition of the azimuth coordinate differs in respect of
the origin. We measure it from the direction of South, while FS has it
counted from North, thus there is a shift of π
between these two
definitions. Consequently, e.g. our terms for the tilts 'out' and 'over',
since they have the same mathematical form as those defined in the FS
model, when positive must be interpreted as toward South and West,
respectively (and not North and East).
Telescope azimuth axis tilt
|
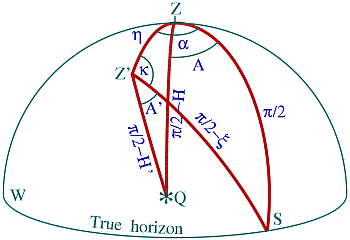
Fig. 1: Sky coordinate relationships for an Alt-Az mounted telescope with
azimuth axis tilted by η in meridian plane α West from South
|
|
Consider a situation when the telescope azimuth axis lies in the meridian
at an angle α
West from the local meridian (i.e., the one that passes through
the South point, S) at an angle η away
from the zenith. In other words,
the apparent zenith has true coordinates:
azimuth α and altitude
π/2 – η.
This situation would mean that the azimuthal track is not
accurately levelled. The transformation from the true coordinates of a source,
azimuth A and altitude H, to the apparent coordinates (as measured by
otherwise an ideal alt-az telescope), A' and H', can be obtained by solving
two spherical triangles having one common side, between the zeniths (true Z and
apparent Z'), and the other two connecting these zeniths with the South point
and with the observed source Q (see accompanying figure). We have obviously:
-
sin(π/2 – ξ)
sinκ = sinα
sin(π/2 – ξ)
cosκ
= –cosη cosα
(these allow to find the intermediate angle κ)
-
sin(π/2 –
H′) sin(A′+
κ) = cos H sin(α – A)
sin(π/2
– H′)
cos(A′+ κ)
= sin H sinη –
cos H cosη cos(α – A)
cos(π/2 –
H′) = sin H cosη
+ cos H sinη cos(α – A).
Reducing these equations leads to the required relations:
| |
|
|
arctan |
cos H sin(α – A)
sinH sinη – cos H cosη
cos(α – A)
|
– arctan |
sinα
–cosη cosα
|
|
| | (1) |
| |
|
| arcsin[sinH cosη
+ cos H sinη cos(α – A)] |
| | (2) |
|
Here, in equation (1), the arctan functions must be
evaluated for a proper quarter basing on the signes of the numerator
and denominator of their arguments.
Splitting this tilt into two orthogonal components, ξ along
the local meridian and ζ towards West (W), one obtains:
(these relations were derived so as to be consistent with
the definitions given in the FS Documentation).
Exact expressions for A' and H' dependence on ξ and ζ
are derived from equations (1) and (2) by substituting
0 and π/2, respectively, for α.
For small η so obtained equations can be easily reduced to
practically useful approximations:
| |
|
|
ηsin(A – α) tan H
≈ (ξsin A
– ζcos A) tan H |
|
| (5) |
| |
|
| ηcos(A – α)
≈ ξcos A + ζsin A |
|
| (6) |
|
Elevation axis and main lobe offsets
The azimuth and altitude axes are ideally mutually perpendicular, so
are altitude axis and optical axis (meaning direction of the power
pattern maximum) of an alt-az telescope. In the following we shall
derive formulae that account for imperfections in these two
perpendicularities, firstly each one separetely, then both combined.
All of them were checked i practical programs.
Elevation axis skew
If the elevation axis is inclined to the plane perpendicular
to the azimuth axis (i.e. plane of the track) by an angle
σ
defined positive when, while A = 0, its West side points above
the plane, then the required relations are obtained by solving
the triangle fomed by the South point, the 'tilted zenith' and
the observed source. We have:
- sin H′ = sin H"σ cosσ
sin(A"σ – A′)
cos H′ = sinσ sin H"σ
and also (useful for derivation of approximation to H"σ – H′)
| tan |
H"σ – H′
2
|
= tan |
A"σ – A′
2
|
|
sin(σ/2)
cos(σ/2)
|
. |
|
Thus the measured horizontal coordinates will be:
| |
|
| | (7) |
| |
|
|
arcsin |
sin H′
cosσ
|
, for H′ ≤ |
π
2
|
|
| | (8) |
| |
|
| π –
arcsin |
sin H′
cosσ
|
, for H′ > |
π
2
|
|
| |
|
Note that the equations (7) and (8)
imply inaccessibility of the sky regions, where
π/2 – |σ| < H′ < π/2 + |σ|,
i.e. within a circular spot of radius equal to |σ| around the 'tilted zenith'.
Corresponding approximations for small σ are:
Beam direction (or box) offset
The main beam direction with respect to the elevation axis
is determined primarily by mutual orientation of the dish, the secondary
mirror and the placement of feeds. Assuming the effective beam declines
from perpendicularity to the elevation axis by an angle β,
counted positive towards East when the dish is directed to A = 0,
one can easily solve a suitably chosen triangle with vertices at
the West point of the elevation axis, the source, and the point
on the 'skewed meridian' passing through the source and placed
π/2 away from the 'skewed zenith' (the sides of
this triangle are π/2 + β,
π/2 –
A"β + A"σ,
and H"σ). Thus noting that-
cos(π/2 + β) = sin(A"β –
A"σ)
cos H"σ, and
|
sin(π/2 + β) = |
sin H"σ
sin H"β
|
|
|
we get immediately:
|
|
|
|
A"σ + arcsin |
sinβ
cos H"σ
|
|
| | (11) |
|
|
|
| | (12) |
|
with conditioning of eq. (12) similar to that of (8)
or using instead the expression H''β =
arccos(cos H"σ √{1 – sin2β/cos2H"σ}/cosβ). Also
note again that the equations (11) and (12)
imply inaccessibility of the sky regions, where
|π/2 –
H"σ| > |β|,
which effectively causes
the circular spot due to the elevation axis skew around the 'tilted
zenith' to enlarge (or shrink) its radius to |σ + β|.
Corresponding approximations for small β are:
Skew and box offset jointly

|
Fig. 2: Sky coordinate relationships for an Alt-Az mounted telescope with
elevation axis skewed by σ and main beam offset
by β with respect to the perpendicular to the
elevation axis. The beam may assume only directions along the broken curve,
thus up to the altitude of π/2 – |σ + β|
|
|
These two effects can be solved for simultaneously. Referring to
Fig. 2 one obtains directly:
sin(π/2 – β)
sin(π/2 + H") = sin(π/2 – H′)
sin(π/2 + A" – A′)
sin(π/2 – β) cos(π/2 + H") = cos(π/2 – H′)
sin(π/2 – σ) – sin(π/2 – H′)
cos(π/2 – σ) cos(π/2 + A" – A′)
cos(π/2 + β) = sin H′sinσ + cos H′cosσ
cos(π/2 + A" – A′).
Reducing these equations leads to the required relations:
| |
| = A′
+
arcsin |
sin H′
sinσ
+ sinβ
cos H′
cosσ
|
|
| | (15) |
| |
|
= arctan |
sin H′
+ sinσ
sinβ
cos H′
cosσ
cos(A" –
A′)
|
|
|
| (16) |
|
Sag
Gravitational pull exerted on telescope structural elements and
thermal deformations cause errors that would be difficult to precisely
predict. To a first approximation the gravitational sag can be modeled
to affect only the altitude coordinate so that
Other offsets
Both the coordinate counters (encoders) are likely to
contain a constant offset (bias) and possibly a rate component. They can
be modeled simply as Ao + ρA
for the azimuth and similar expression for the altitude counter.
Various unmodeled effects are almost sure to be present in practice
and must be accounted for basing on analysis of measurements
made with a particular design. Frequently useful are ad hoc
model components proportional to the sine and cosine of the coordinates
and their multiples.
Complete model
Groupping all the described contributions to overall position offsets
in both coordinates one may construct a complete form of the model.
Preliminary analysis of actual observational data for the RT32
showed that the approximations derived above are really very good
and not all the mentioned ad hoc components are useful.
These allowed to reduce the model to the following two expressions:
|
|
|
|
Ao + (ξsin A – ζcos A + σ) tan H + |
β
cos H
|
+ p9sin2A + p10cos2A | |
(18) |
|
|
|
| Ho + ξcos A +
ζsin A + γcos H + p8sin H +
p11sin2A + p12(condition) |
|
(19) |
Here follows a Fortran subroutine to calculate azimuth
(dAz) and altitude (dAlt) offsetts in degrees for given
true coordinates, Az and Alt (in radians) and the model
parameters, according to exact formulation.
subroutine Model(Az,Alt,dAz,dAlt,p)
c RT32 model for azimuth (Az) and altitude (Alt) pointing
c offsets, dAz, dAlt. Parameters p are in degrees, so are the
c offsets while Az and Alt must be supplied in radians.
c It is more accurate version of Model3A with exact analytical
c expressions for effects of telescope tilt, elevation axis
c skew and main lobe offset.
implicit real*8 (a-h,o-z)
real*4 Az,dAz,Alt,dAlt,p(12),Hjump
data pi/3.141592653589793d0/
arcsin(arg)=dasin(dmin1(1.d0,dmax1(-1.d0,arg)))
xi=p(5)*pi/180d0 ! tilt out (toward Az=0 deg)
zeta=p(6)*pi/180d0 ! tilt over (toward Az=90 deg)
sigma=p(3)*pi/180d0 ! skew
beta=p(4)*pi/180d0 ! beam (box) offset
sh=dsin(Alt)
ch=dcos(Alt)
c Tilt
se=dsign(dsqrt(dsin(xi)**2+dsin(zeta)**2),ch)
ce=dsqrt(1-se*se)
alfa=datan2(dsin(zeta),dsin(xi))
AT=datan2(ch*dsin(alfa-Az),sh*se-ch*ce*dcos(alfa-Az))
*-datan2(dsin(alfa),-ce*dcos(alfa))
hT=dasin(ce*sh+se*ch*dcos(alfa-Az))
AT_Az=AT - Az
if(ch.lt.0d0) then
AT_Az=pi-AT_Az
hT=pi-hT
endif
c Skew & box offset together (good also for hT > pi/2)
dAz=arcsin( (dsin(sigma)*dsin(hT)+
*dsin(beta))/(dcos(hT)*dcos(sigma)) )
hb=datan2(dsin(hT)*dcos(sigma)
*+cos(hT)*sin(sigma)*dsin(dAz),dcos(hT)*dcos(dAz))
dAz=dmod((dAz+AT_Az)*180/pi,360d0)
*+p(1) ! encoder offset
*+p(9)*sin(2*Az) ! ad hoc
*+p(10)*cos(2*Az) ! ad hoc
if(dabs(dAz).gt.180d0) dAz=dAz-dsign(360d0,dAz)
dAlt= (hb-Alt)*180/pi
*+p(2) ! encoder offset
*+p(7)*ch ! sag
*+p(8)*sh ! ad hoc
*+p(11)*sin(2*Az) ! ad hoc
if(Hjump(Az,Alt).gt.0.) dAlt=dAlt+p(12)
end
function Hjump(Az,Alt)
c Ad hoc function used to model the observed jump in altitude
c offsets. With Alt<0 it returns the altitude of the jump.
data pi/3.141593/
Hjump=0
A=Az*180/pi
H=Alt*180/pi
if(A.le.0.) then
Hj=65+7*cos(Az/2)
else
Hj=55+((A-95)/90)**2*15
endif
if(Alt.gt.0..and.Hj.le.H) Hjump=1
if(Alt.lt.0.) Hjump=Hj
end
|
The described approximations were implemented according to equations
(18) and (19) in this routine:
subroutine ModelA(Az,Alt,dAz,dAlt,p)
c RT32 model for azimuth and altitude offsets; parameters p are
c in degrees. Should be good for Alt > pi/2 since then p5 and
c p6 both get opposite signs relative to pi - Alt direction and
c assuming p9 and p10 are connected with wheels position on
c the azimuth track.
real*4 p(12)
data pi/3.141593/
c ********* Model for azimuth offset **********
t=tan(Alt)
dAz=p(1) ! encoder offset
*+p(3)*t ! axis skew
*+p(4)/cos(Alt) ! box offset
*+p(5)*sin(Az)*t ! tilt out (toward Az=0 deg)
*-p(6)*cos(Az)*t ! tilt over (toward Az=90 deg)
*+p(9)*sin(2*Az) ! ad hoc
*+p(10)*cos(2*Az)
dAz=amod(dAz,360.)
if(abs(dAz).gt.180.) dAz=dAz-sign(360.,dAz)
c ********** Model for altitude offset **********
A=Az
if(Alt.gt.pi/2) A=pi+A
dAlt= p(2) ! encoder offset
*+p(5)*cos(A) ! tilt out (toward Az=0 deg)
*+p(6)*sin(A) ! tilt over (toward Az=90 deg)
*+p(7)*cos(Alt) ! sag
*+p(8)*sin(Alt) ! ad hoc
*+p(11)*sin(2*A) ! ad hoc
if(Hjump(Az,Alt).gt.0.) dAlt=dAlt+p(12)
end
|
This Fortran subroutine must not be used for points very close to
the zenith (say, closer than 0.1 degree in the RT32 case).
However it
was programmed to be applicable for pointing in plunge, i.e. for
altitudes (Alt) some distance behind π/2,
provided the p9 and p10 parameters are interpreted to be
related to the wheels position on the azimuth track. So far, however,
this option of pointing in plunge has not been tested against measurements
(for a time being, the steering system prevents such observations).
Data analysis
The offsets from the true source positions were recently
measured independently for both the coordinates at a few thousand points.
These measurements were performed using special software described in the
32 m
Radio Telescope — Technical Description and Observer's Handbook
(Chapter VIII, presently
available
only in Polish). Assumed source positions were the catalogue equatorial
coordinates precessed to the epoch of observations
and converted to the azimuth and zenith distance at the RT32 latitude and
longitude.
For the purpose of model fitting these data at the outset have been
corrected by removing from them a few of known effects, namely:
-
1) Nutation of catalogue source coordinates (amplitude about 17")
2) Stellar and diurnal aberration (20")
3) UT1 – UTC offset due to variable Earth rotation (13")
4) Polar motion effect on RT32 coordinates (17 m)
5) Mean atmospheric refraction (~60"/tan H).
(The item No 4 above is practically negligible, but has been included for
completeness.)
Corrected data were then used in a fitting process to get the estimates
of model parameters, simultaneously for azimuth and altitude models.
Simultaneity is essential, because the two approximation models have two
(tilt) parameters in common, and there are more common parameters in
the exact version. To this end the two data sets were glued together
to be seen by a standard weighted least-squares fitting program as
one while the function being fitted switched between the two models
depending on datum currently called by the fitting program.
The parameter estimation was done in a few iterations, which differed
in number of points effectively used for fitting. In the first iteration
step all altitude offsets were used with equal weights and the azimuth
offsets were weighted proportionally to the cosine of altitude. Before
each successive step data, that deviated from the fit so far obtained
by more than certain level, were downweighted by a factor of 1000.
This somewhat subjective (because the final level choice depends
on a user) procedure allowed to almost automatically eliminate
any significant influence of outliers on the final solution. By the same
token any weird behaviour of the telescope is left essentially undistorted
and stands clearly out in the residuals for further study.
The example presented in the remainder of this document is a solution
obtained at the rejection level
arbitrarily set at 0.007 degrees, which effectively eliminated from
the fit about a third of original data (those that deviated from
the previous fit by more than this level). In this solution we have
combined measurements collected in two separate campaigns, March 15 to
June 12 in 2003, and January 29 to May 6 in 2004. Alterations,
connected with the RT32 maintenance, carried out in the intervening
period resulted in the relative beam offset of 0.017±0.001 degrees (as
deduced from comparison of an earlier model based on 2004 data with
the raw 2003 data). This required correction of the measured 2003 azimuth
offsets by subtracting 0.017/cos H degrees before the final fit of all
the data.
RT32 Model3 parameters (without refraction)
All ~5600 data collected in 2003 and 2004 were analysed
and 3684 points fitted with RMS of 12.8" = 0.003550 deg
p Parameter (deriv.) Value
1 Zero Az (1) -177.4+/- 1.9" = -0.049282+/-0.000528 deg
2 Zero Alt=pi/2-z (1) -214.7+/-10.8" = -0.059632+/-0.003008 deg
3 Skew Az (tg Alt) 34.0+/- 2.5" = 0.009452+/-0.000702 deg
4 Box Az (1/cos Alt) -47.7+/- 3.0" = -0.013255+/-0.000835 deg
5 Tilt South Az,Alt 5.0+/- 0.2" = 0.001393+/-0.000056 deg
6 Tilt West Az,Alt -1.1+/- 0.2" = -0.000304+/-0.000057 deg
7 Sag Alt (cos Alt) 112.6+/- 8.7" = 0.031273+/-0.002407 deg
8 Ad hoc Alt (sin Alt) 41.2+/- 7.0" = 0.011458+/-0.001949 deg
9 " Az (sin 2Az) -42.3+/- 0.3" = -0.011751+/-0.000094 deg
10 " Az (cos 2Az) 16.3+/- 0.3" = 0.004539+/-0.000083 deg
11 " Alt (sin 2Az) 15.4+/- 0.4" = 0.004291+/-0.000123 deg
12 " Alt jump (1) -73.4+/- 2.2" = -0.020392+/-0.000621 deg
|
Although the above table may indicate quite nice fit of the model and
data, we would like to point out that individual parameters are not to be
relied upon too much and the errors given are overoptimistic. This conlusion
is based on comparison with earlier fits to parts of data included in this most
complete collection. We believe this is due to high correlation between some
of the 12 parameters. In particular, the correlation of the parameter No 1 in
the table (azimuth encoder offset) with the 3rd and 4th
is as high as about 0.95 and still
higher correlation exists between the parameters 2, 7 and 8.
For our purposes, however, the noted property is not of real moment, since
we are interested primarily in stability and goodness of the overall fit.
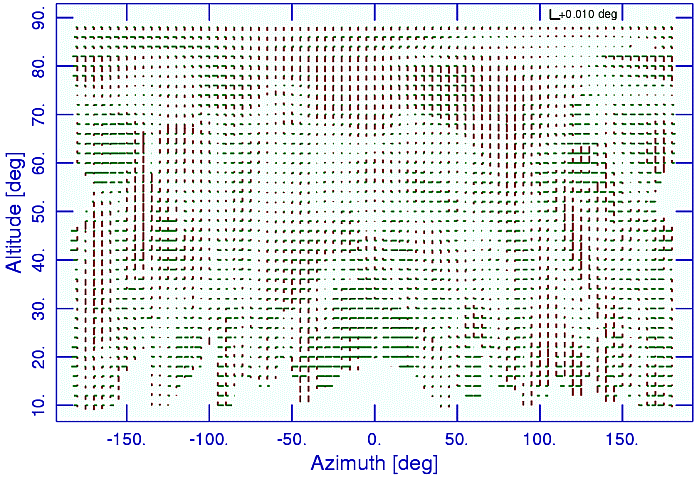
As seen in Fig. 3, the residua from this model, which was
fitted to about 66 % of the data, are generally small on the whole Alt-Az plane.
Among 5615 (2758 altitude offsets and 2857 azimuth offsets) plotted
points we have found as many as 4987 (2376 plus 2611), i.e. about 89 %, with
residua smaller than 0.01 deg.
There are, however, whole sequences of measurement points with evidently
systematically high departures. These that lie in close proximity of apparently
good measurements may be assumed to be spurious and resulting e.g. from some error
connected with particular observing session. More fundamental seems the abrupt
fall of the altitude offsets when moving the telescope to higher altitudes
and modeled as the 'jump'. The red line in the plot
approximates the location of this jump.
|
Fig. 3: Residuals from RT32 pointing model fitting. Majority of them lie well below
0.01 degree in magnitude (a scale bar of +0.02 degree is shown near to the upper
right corner), however there are areas of larger and systematic mismatching, most
notably in the altitude case
(lower figure) around the red curve, which marks a discontinuity (the jump in
the model) of 0.02 degree. These need further investigation (a working hypothesis
is that they might be due to a mechanical problem related to the subreflector)
|
|
Fig. 4: Smoothed residuals from Model3. The vertical bars correspond to the altitude
offsets and the horizontal ones to the azimuth offsets. Each smoothed value is an
average of residuals within 5° off the point, weighted with cosine function of
the angular distance scaled to π/2 at the edge of this
circular area. Averaged residuals were the same as in Fig. 3 except that those
that exceeded 0.01° in absolute value have been suppressed.
|
|
Fig. 5: Distribution of residuals from Model3 along the azimuth (left panels) and
along altitude coordinate (right panels). The upper panels show the residuals
of azimuth offsets, the lower panels show the residuals of altitute offsets.
|
Lookup table of offsets
The model of azimuth offsets described in the preceding section can be used
directly by the telescope steering system, but the elevation offsets must
still be supplemented with a model for mean atmospheric refraction,
similar to that employed for initial correcting of the raw offsets.
The RT32 steering system corrects the true coordinates basing on
numerical data given in the form of a regular array. The array consists
of 4 colums that represent the azimuth, zenith distance, azimuth offset
and zenith distance offset, in this order, all these quantities being
expressed in degrees. Each row corresponds to different coordinates
in step of 1 degree covering the range:
–270 through +270 in azimuth, and
–5 through 89 in zenith distance,
so that there are 541×95 = 51395 rows or offset pairs
in the lookup table.
Its structure, using the Model3 as an example, looks like this:
-270 -5 -0.0257069 0.0722200
-270 -4 -0.0189086 0.0713727
...............................
-270 89 -0.0668883 -0.3294362
-269 -5 -0.0252313 0.0723455
.
.
.
270 88 -0.0668030 -0.2543178
270 89 -0.0669250 -0.3300445
|
Such an ASCII table is further compressed to a binary format
before submitting to the steering program. An RT32 operator invokes
this particular table under the name '3model'.
The following tables give further details on the 3model correction table.
Columns correspond to the azimuth given at their top in degrees. Rows correspond
to the zenith distance (90° – H) given in degrees in the leftmost column.
The values were here rounded to the nearest integer number of indicated units.
Extracts from the 3model CORRECTION TABLE
Azimuth offsets as obtained from the exact model [0.001 deg]
z\Az -180 -150 -120 -90 -60 -30 0 30 60 90 120 150 180
-5.00 3 -2 -2 6 15 12 -4 -24 -33 -26 -9 2 3
0.10-2366-2758-3007-3040-2852-2498-2078-1704-1468-1430-1601-1942-2366
10.00 -69 -85 -92 -84 -70 -62 -66 -74 -77 -69 -58 -57 -69
20.00 -58 -73 -78 -70 -57 -51 -57 -67 -71 -63 -51 -48 -58
30.00 -55 -69 -74 -66 -53 -48 -54 -66 -70 -62 -50 -46 -55
40.00 -54 -68 -73 -65 -52 -47 -54 -65 -69 -62 -49 -46 -54
50.00 -54 -67 -72 -64 -52 -47 -54 -66 -70 -62 -50 -46 -54
60.00 -55 -68 -72 -64 -52 -47 -54 -66 -71 -63 -51 -46 -55
70.00 -56 -68 -73 -65 -52 -48 -55 -68 -72 -64 -52 -47 -56
80.00 -57 -69 -74 -66 -53 -49 -56 -69 -73 -65 -53 -49 -57
89.00 -58 -70 -75 -67 -54 -50 -58 -70 -75 -67 -54 -50 -58
[approximate model has the form: p1 + p4/sinz + (p3 + p5*sinAz
- p6*cosAz)/tanz + p9*sin2Az + p10*cos2Az]
Zenith angle offsets (refraction and jump included) [0.001 deg]
z\Az -180 -150 -120 -90 -60 -30 0 30 60 90 120 150 180
-5.00 71 68 68 73 77 78 74 70 69 72 75 75 71
0.10 70 66 65 68 71 71 67 63 64 69 73 73 70
10.00 62 58 57 60 63 63 59 56 57 61 65 66 62
20.00 54 50 50 53 35 35 31 48 49 53 58 58 54
30.00 26 22 22 25 28 27 23 20 41 46 50 30 26
40.00 19 15 14 17 20 20 16 12 13 18 22 22 19
50.00 10 6 6 9 12 11 8 4 5 9 14 14 10
60.00 0 -4 -4 -1 2 1 -3 -6 -5 -1 4 4 0
70.00 -16 -20 -21 -18 -15 -15 -19 -23 -22 -18 -13 -13 -16
80.00 -60 -64 -65 -62 -59 -59 -63 -66 -65 -61 -57 -56 -60
89.00 -328 -332 -333 -330 -327 -327 -331 -335 -334 -329 -325 -325 -328
[approximate model has the form: -p2 - p5*cosAz - p6*sinAz - p7*sinz
- p8*cosz - p11*sin2Az - p12(conditionally) - refraction]
Differences: approximate model - exact model [0.0001 deg]
Azimuth differences
z\Az -180 -150 -120 -90 -60 -30 0 30 60 90 120 150 180
-5.00 0 0 0 0 0 0 0 0 0 0 0 0 0
0.10 -319 -281 -125 93 274 340 289 178 65 -38 -146 -254 -318
10.00 0 0 0 0 0 0 0 0 0 0 0 0 0
..... ........................ (all zeroes) ........................
89.00 0 0 0 0 0 0 0 0 0 0 0 0 0
Zenith angle differences
z\Az -180 -150 -120 -90 -60 -30 0 30 60 90 120 150 180
-5.00 0 0 0 0 0 0 0 0 0 0 0 0 0
0.10 1 1 1 1 1 1 1 1 1 1 1 1 1
10.00 0 0 0 0 0 0 0 0 0 0 0 0 0
..... ........................ (all zeroes) ........................
89.00 0 0 0 0 0 0 0 0 0 0 0 0 0
|
Acknowledgements:
This document is based on years of efforts
of the TRAO staff. I would like to especially thank my colleagues,
Andrzej Kus, Marcin Gawroński and Radosław Zajączkowski, whose help and
contribution were essential to finalizing the presented work.
Translated from
TEX
by
TTH,
v. 3.59 on 16 May 2004, 19:55|
Last modified: 2004.06.24 | |