This page is in Polish, however abstract,
tables and figure captions are in English.

Optyczne własności RT32 związane z położeniem subreflektora

Skok ten odpowiada zmniejszeniu porawki dodawanej do nominalnych odległości zenitalnych, z, we wspomnianym obszarze, np. z 0.060 do 0.040°, przy przejazdach z obszarów bliższych zenitowi ku horyzontowi. Oznacza to, że po przeskoku teleskop trzeba skierować nieznacznie w górę (zmniejszyć współrzędną z). To z kolei oznacza, że wiązka charakterystyki kierunkowej na skutek przeskoku podczas przejazdu w dół, w kierunku horyzontu, obniżyła się. Przyjmiemy dalej, że ten kierunek odchylenia wiązki, kierunek wzrostu odległości zenitalnej, w dół, jest dodatni. W takim kierunku przesuwa się wiązka, gdy:
— cały teleskop albo tylko sam paraboloid obróci się w tę właśnie stronę (ku horyzontowi),
— oświetlacze w ognisku wtórnym przestawi się w przeciwną stronę, w górę,
— lustro Cassegraina obróci się wierzchołkiem nieco w dół, ku horyzontowi,
— to samo lustro przesunie się prostopadle do osi optycznej teleskopu w górę.
Wielkość kąta przesunięcia wiązki i kierunek zestawiono w zależności od przyczyny w poniższej tabeli. Kolumny 'Rate of change' podają o ile stopni lub minut łuku przesunie się wiązka na podaną jednostką czynnika powodującego zmianę. Są tam dwie kolumny: pierwsza według obliczeń opartych o znane z literatury wzory przybliżeń optyki geometrycznej, a druga bazująca na metodzie 'ray-tracingu' z wykorzystaniem przygotowanego w 2005 r. w Centrum Astrnomii specjalnego programu OptiCass. Jak widać uzyskane wartości są bardzo zbliżone (większe różnice można stwierdzić dopiero przy większych wartościach 'offsetów', a wynikają one głównie z ograniczeń klasycznych przybliżeń) i podajemy je tutaj jedynie dla nadania wiarygodności obliczeniom wykonanym za pomocą zupełnie nowego oprogramowania.
W ostatniej kolumnie Tabeli 1a widnieje wielkość efektu, który mógłby spowodować obserwowane przesunięcie wiązki o 0.02° (czyli 0.02° podzielone przez 'rate' z poprzedzającej kolumny po przeliczeniu na podane jednostki).

Tabela 1b zawiera bardziej szczegółowe dane wykorzystane częściowo w Tab. 1a.

Tab. 1a.

Offsets of RT32 with OCRA resulting in beam shift of 0.02 deg The column Class. contains values derived from classical approach while column Ray-T has them obtained with ray-tracing method Effect -- Rate of change -- 0.02 deg --- Subreflector motions -------------- Class. Ray-T Units requires Lateral translation -3.39 -3.40 °/m -5.9 mm Vertical rotation around actual pivot 4.57 4.54 '/° +0.264 deg corresponding vertex translation +7.1 mm Rotation about prime focus 6.27 6.27 '/° +0.190 ° corresponding vertex translation 3.5 mm Rotation about vertex 10.0 10.2 '/° +0.120 ° corresponding edge translation +3.4 mm Rotation about secondary focus - 26.3 '/° +0.046 ° corresponding subreflector sag +7.3 mm Rotation about paraboloid vertex - 29.8 '/° +0.067 ° corresponding main dish translation +11.9 mm ------ Other offsets ------------------ Main dish translation -3.98 -3.98 °/m -5.0 mm Feed lateral offset (second. focus) -35.2 -35.2 '/m -34.1 mm

Tab. 1b.

Some RT32 characteristics at 30 GHz valid for small offsets (based on classical optics approach; 12 dB parabolic on pedestal or Gaussian illumination function assumed) Half power beam width .......................... 0.0208 [°] First side lobe power level due to taper ....... 0.5351 [%] Gain loss due to diffraction at subreflector ... 1.6493 [%] Beam deviation factor, prime focus ............. 0.7780 dimensionless Beam deviation factor, secondary focus ......... 0.9961 dimensionless Beam dev. due to primary translation ........... -3.9798*Xoff/m [°] Beam dev. due to primary rotation .............. 1.7780*tilt/° [°] Beam dev. due to secondary translation ......... -3.3925*Xoff/m [°] Beam dev. due to secondary rotation about vertex 0.1670*tilt/° [°] Beam dev. due to secondary rotation about focus 0.1046*tilt/° [°] Beam dev. due to secondary rotation about pivot 0.0761*tilt/° [°] Beam dev. due to feed translation in sec. focus -0.5873*Xoff/m [°] Feed offset per beam width, prime focus ........ -0.0052*NoOfBeams [m] Feed offset per beam width, secondary focus .... -0.0355*NoOfBeams [m]

Z tych obliczeń wynika, że jeśli źródłem problemów jest lustro Cassegraina, to można oczekiwać przesunięć jego elementów o łatwo mierzalne, kilkumilimetrowe wartości. Bardzo prawdopodobne miejsce luzu, w Tab. 1a czynnik wymieniony na drugiej pozycji, oznaczałoby ok. 7 mm opadanie wierzchołka lustra na ramieniu o długości 1.054 + 0.480 m = 1.534 m (punkt obrotu lustra w tej płaszczyźnie znajduje się na osi głownej teleskopu, ok. 0.5 m ponad ogniskiem pierwotnym).

W tym kontekście warto zauważyć, że wyznaczone wcześniej z pointingu przesunięcie –0.017° w azymucie takie, że nowe poprawki są mniejsze (co wynika z konieczności dodania tej wartości przeskalowanej cosinusem wysokości przy redukcji wcześniejszych pomiarów do obecnych), zgodnie z Tab. 1b oznacza przesunięcie lustra Cassegraina o –0.017°/(–3.3925 °/m) = 0.005 m. Ujemna poprawka w azymucie wyraża wiązkę przesuniętą o tę wartość (bezwzględnie) ku większym azymutom (na zachód od południka) względem nominalnego kierunku. Ta argumentacja prowadzi do wniosku, że między wiosną i jesienią 2003 r. lustro uległo przesunięciu o ok. 5 mm w kierunku przeciwnym do wiązki, czyli w lewo patrząc od strony oświetlaczy teleskopu skierowanego na horyzont.

W obecnym modelu poprawek widnieje składnik (4-ty parametr w Model3, Box offset) odpowiadający poprawce w azymucie –0.013255°/sin(z), czyli odchyłce wiązki charakterystyki kierunkowej o ok. 0.013° w prawo, czyli lustra o 0.013/3.3925 m = 4 mm w lewo. Nasuwa się skojarzenie, że te 4 mm to może bezpośredni skutek wyżej opisanego przesunięcia o 5 mm. Czy takie przesunięcie lustra jest praktycznie znaczące dla własności optycznych radioteleskopu?

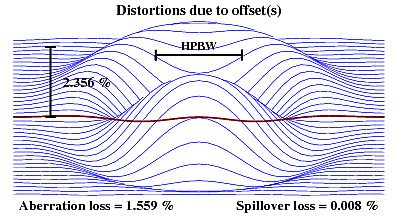
Fig. 1: One of components of the present model for azimuth pointing offsets (namely parameter No 4 or Box offset) can be related to a subreflector lateral displacement of about 4 mm. This figure presents distortions of power pattern of the RT32 telescope at 30 GHz expected of lateral shift of its secondary mirror by 4 mm. Plotted are vertical sections through the differential beam. In the case presented here tracing was made for 2904 rays and the DFTs calculated at 1681 points on a u-v plane square (~5 beamwidth on a side) centered at the beam. The percentages given in this picture however do not change appreciably when the number of rays is increased to some 15000.

Jak pokazują obliczenia samo poziome przesunięcie lustra o 4 mm przy obserwacjach na fali 1 cm (30 GHz) powoduje straty sygnału (skuteczności anteny) o ok. 1.57% w stosunku do sytuacji idealnego zjustowania optyki. Poziome przesunięcie można często prawie całkowicie skompensować obrotem lustra w płaszczyźnie zawierającej kierunek przesunięcia i oświetlacz, ewentualnie z translacja ogniskującą (wzdłuż osi optycznej). W przypadku RT32 obrót boczny lustra odbywa się jednak wokół ogniska, co praktycznie nie pozwala na kompensowanie bocznych jego translacji. W istocie same aberracyjne straty (tzn. spowodowane astygmatyzmem i comą) można w ten sposób zmniejszyć, ale tylko do ok. 1.3% i przy równoczesnym wzroście strat na 'spillover' (spowodowany tym, że wiązka wyemitowana z oświetlaczy po odbiciu od lustra Cassegraina nie w całości trafia w główny reflektor) do ok. 0.5% (tych ostatnich w naszym przypadku nie można znacząco zmniejszyć korekcją kierunku oświetlaczy). W sumie więc takie korygowanie nie jest efektywne, a niewielka poprawa strat aberracyjnych w istocie nie opłaca się. Podobnie nieefektywne byłyby próby przesunięcia oświetlacza poza ognisko. Wydaje się więc, że jedynym sposobem na wyeliminowanie takiej 1.5-procentowej straty (która, bądź co bądź, odpowiada ujęciu ok. 12 m² z apertury, czyli usunięciu 5 paneli!) jest zatem korekcja samej przyczyny, czyli poziomego ustawienia subreflektora. Dla niższych częstości straty z tego offsetu lustra Cassegraina są mało istotne. Np. na 12 GHz wynoszą one ok. 0.26%, a na 5  — już tylko ok. 0.06%

Zniekształcenia wiązki głównej charakterystyki kierunkowej wynikające z 4 mm bocznego przesunięcia lustra pokazuje rysunek Fig. 1. Są tam wykreślone różnice między znormalizowanymi charakterystykami mocy RT32 z domniemanym przesunięciem i bez niego. Podane wyliczenia uzyskano z 'ray-tacingu' blisko 3000 promieni (za pomocą programu OptiCass). Po około pięciokrotnym zwiększeniu tej liczby, do 14600 śledzonych promieni, otrzymuje się niewiele różne oceny: straty odbieranej mocy na poziomie 1.56% (w tym 1.549% stanowią zaznaczone na rysunku aberracje) i zakres odkształceń charakterystyki od –1.767 do 2.347% (co trzeba porównywać z liczbami –1.772 i 2.356% otrzymanymi dla 3000 promieni).

Drugie możliwe źródło tego 0.013-stopniowego składnika modelu odchyłek to obrót lustra Cassegraina o –0.127° (tj. wierzchołkiem w prawo dla patrzącego z miejsca oświetlaczy teleskopu skierowanego na horyzont) wokół ogniska pierwotnego. Tego typu błąd ustawienia lustra w praktyce nie powoduje żadnych istotnych strat (bo są one znacznie poniżej 0.01%) aberracyjnych, a jedynie niewielkie (0.08%) straty na spillover.

Dyskusja nowych danych pozycjonowania

— niedoskonałość samego modelu poprawek (najlepiej dopasowany do pomiarów model, model3, pozostawiał ok. 11% danych odbiegających od niego o więcej niż 0.01°)
— model nie uwzględnia odchyłek zależnych od zmiennych czynników takich jak aberracja światła, nutacja i mniej znaczące wpływy ruchu bieguna Ziemi, nierównomierności rotacji Ziemi (zmienna i niezerowa wartość UT1 – UTC), zmienności refrakcji (w funkcji warunków atmosferycznych) oraz dyskretności samej tabeli poprawek (tabela poprawek nazywana model3 efektywnie wykorzystuje tylko wartości tego modelu z węzłów siatki wyznaczonej przez nieparzyste wartości azymutu i odległości zenitalnej wyrażone w stopniach)
— istnienie nieciągłości (0.02° skoku) w poprawkach w niestabilnym miejscu przy zmianach odległości zenitalnej RT32.

Poniższy rysunek przedstawia korekcje na dwa najważniejsze z wymienionych wyżej zmiennych czynników obliczone dla każdego z pomiarów RF. Ich znak jest taki, że należy je dodać do zmierzonych błędów pointingu, aby uzyskać błędy samego modelu poprawek. Dwa panele zawierają te same dane wykreślone raz w funkcji azymutu, raz — elewacji (wysokości).

Fig. 2: Aberration and nutation corrections to the RT32 telescope pointing, as required in addition to permanent look-up table, computed for the analysed sample of measurements performed in March and April 2005. The same data are plotted against the azimuth (upper panel) and altitude (lower panel)

Widać stąd, że przynajmniej w analizowanych tu danych przyczynki od zmiennych czynników nie przekraczają wartości 0.01°, jednak mniej więcej połowa z nich przewyższa połowę tej granicy. Takie wartości są już znaczące przy wiązce o szerokości połówkowej 0.02° (jaką ma RT32 na 30 GHz). Błędy pointingu bez i z powyższymi poprawkami przedstawia rysunek Fig. 3.

Fig. 3: Observed (blue) and corrected (red) pointing errors in the azimuth (upper panel) and zenith distance (lower panel). These plots show that the errors are dominated by still unaccounted systematic effects. Note however that the presence of the 0.02° jump becames discernced in the zenith distance errors after applying corrections for aberration and nutation only; see also Fig. 4. The jump seems to be mainly responsible for the standard deviations remaining practically the same before and after applying the corrections. Nevertheless, the percentage of errors exceeding 0.01° in absolute value fell down due to the two corrections from 17% to 8% in azimuth and from 36% to 23% in zenth distance (each set, of the two corresponding to these two coordinates, consisted of 314 measurements).

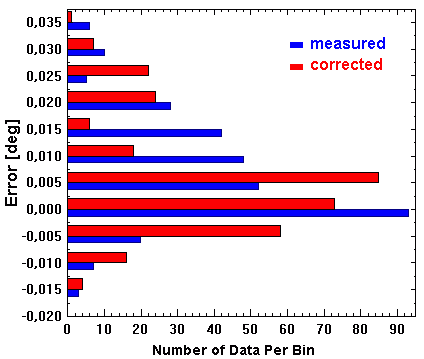
Fig. 4: Error distributions for uncorrected (blue) and corrected (red) pointing measurements in the zenith distance. This diagram reveals the presence of 0.02-degree jump in the corrected errors (bars clearly peaking near 0.02° with the main peak near –0.005 to 0.005°).

Rysunki Fig. 3 pokazują, że w obecnej sytuacji korygowanie danych na zmienne czynniki niewiele poprawia jakość pointingu mierzoną rozrzutem błędów ze względu na duże błędy innego pochodzenia. Niemniej, wprowadzenie tylko dwóch największych poprawek do analizowanych tu 314 pomiarów spowodowało zmniejszenie odsetka błędów przekraczających 0.01° z 17% do 8% w azymucie i z 36% do 23% w odległości zenitalnej. Poprawienie dodatkowo na efekty związane z orientacją Ziemi (zasadniczo UT1 – UTC, które w tym okresie wynosiło ok. –0.6 s czyli –0.002°) redukuje jeszcze wymienione azymutalne 8% do 6%. Średnio mamy więc ok. 14% procent błędów przewyższających 0.01°, co jest bliskie owym 11% 'przysługującym' modelowi. Nadwyżkę można bez skrępowania spisać na karb większego ułamka obserwacji w pobliżu uskoku obecnego w tabeli poprawek, gdyż dwa słupki na rysunku Fig. 4, w rozkładzie poprawionych błędów we współrzędnej z, dla wartości 0.020 i 0.025° zawierają aż około 15% wszystkich pomiarów. Gdyby ująć z wyżej podanego odsetka 23% te 15%, mielibyśmy praktycznie ten sam procent (ok. 8) błędów przekraczających umowną granicę 0.01° w obu współrzędnych w tej próbce pomiarów, czyli znacznie lepiej niż w przypadku danych użytych pierwotnie do dopasowania modelu!

Porównanie charakteru rozkładu błędów azymutu (górny panel Fig. 3) z analogiczną statystyką pomiarów z kampanii 2003 i 2004 (górny lewy panel Fig. 5 w innym pliku reprodukowany tutaj jako Fig. 5.) wskazuje, że tamte odstępstwa przejawiają się częściowo w tych pomiarach. Np., struktura w obszarze między azymutami ok. 50 i 100° zdaje się być szczególnie wyraźnym i trwałym zjawiskiem i powinna łatwo dać się usunąć przez dodanie liniowego składnika do obecnego modelu poprawek. Podobnie stabilna sytuacja występuje w pobliżu A = 180° i być może w innych zakresach azymutu, ale mamy jeszcze trochę za małą statystykę, by się przy tym upierać.

Fig. 5: Residua from the original Model3 fit to data of 2003 and 2004 in azimuth (taken from Fig 5. in another file). Compare it with the upper panel of Fig. 3 to note a few common features, especially one between 40 and 80° in azimuth.

Zmienne poprawki a System Sterowania

  Niewątpliwie najwiekszy wpływ na widome położenia radioźródeł mają zjawiska aberracji i nutacji. Relatywistyczna aberracja (roczna i dobowa) wynika z ruchu obiegowego Ziemi wokół Słońca i rotacji Ziemi wokół własnej osi, ma więc okresowość roczną i dobową. Maksymalne przesunięcie położenia źródła w wyniku tego efektu rocznego wynosi ok. 20" czyli ok. 0.006°, zaś składnik dobowy na naszych szerokościach geograficznych nie przekracza 0.2", można go więc pominąć w praktyce naszych obserwacji. Przybliżone wzory na poprawki współrzędnych równikowych na efekt aberracji można znaleźć np. w rocznikach Astronomical Almanac.

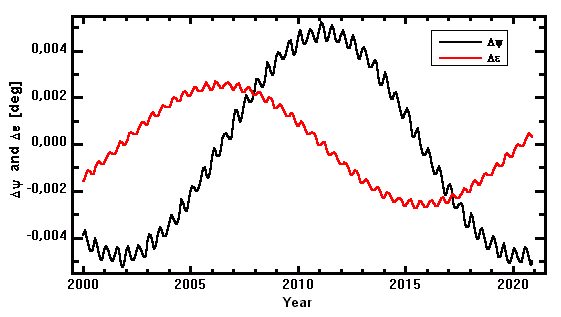
Fig. 6: Components of nutation in ecliptic longitude Δψ and inclination of equator to ecliptic Δε. These components correspond approximately to maximum change in source right ascesion and declination, respectively.

Drugi ze wspomnianych czynników to nutacja osi rotacji Ziemi w przestrzeni, którą w pełnej precyzji opisuje dość złożony algorytm (kilkadziesiąt do ponad tysiąca członów, zależnie od teorii). Dla celów sterowania naturalnie nie potrzebujemy bardzo wysokiej precyzji i, jak widać na załączonym rysunku (Fig. 6), możemy ograniczyć się nawet do dwóch sinusoidalnych składników o ok. 19-letniej okresowości i amplitudach ok. 17.2" i 9.2". Pierwszy z nich należy dodać do długości ekliptycznej radioźródła (obliczonej ze średnich współrzędnych równikowych epoki), a drugi do średniego nachylenia ekliptyki do równika (ε) i przeliczyć współrzędne ekliptyczne źródła z powrotem na równikowe. Alternatywne uproszczenie można zaczerpnąć również z Astronomical Almanac.

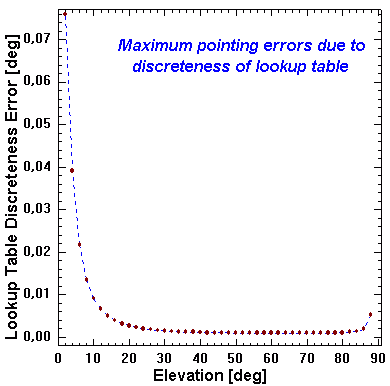
Fig. 7: Corrections of nominal coordinates presently are done every 2° of azimuth and zenith distance using lookup table data at odd number of degrees of the coordinates. Such discreteness leads to errors in pointing that are largest near to knots of even values of the coordinates expressed in degrees. For given knot the root of sum of squared errors in azimuth and zenith distance has been calculated at four points ±0.00001° away from every knot in either coordinate. This plot shows the largest value of such errors of all knots at each even degree of elevation starting from the telescope horizon (i.e. elevation of 2°). Between altitudes 24 and 86° this pointing error does not exceed 0.002°, and falls below 0.001° for altitudes 50 to 78°.

Trzeci co do ważności ze zmiennych czynników wpływających na pointing to różnica między czasem UT1 (wyrażającym rzeczywisty kąt obrotu Ziemi w jej dobowym ruchu) i czasem, który używamy podczas obserwacji, UTC, który biegnie zasadniczo (pomijając sekundy przestępne) równomiernie. Różnice mogą zbliżać się nawet do całej sekundy (obecnie jest to ok. –0.6 s). Zmierzone wartości różnicy są dostępne w bazach danych centrów IERS (np. pliki EOPc04.yy dla poszczególnych lat yy). Dla nas jednak ważniejsze są predykcje, które można znaleźć w uaktualnianym co tydzień IERS Bulletin-A. Biuletyn ten zawiera tabele predykcji UT1–UTC na okres roku. Znajdujemy tam także wyrażenia analityczne typu UT1–UTC = –.5323 – .00031 (MJD – 53402) – (UT2–UT1), gdzie ostatni człon (przyczynki sezonowe) stanowią 4 składniki sinusoidalne, jednak można je pominąć, gdyż razem nie przekraczają 0.04 s (przytoczony wzór wzięto z biuletynu z dnia 27 stycznia 2005). Takie wyrażenia nie są wprawdzie równoważne predykcjom podanym w postaci tabeli wartości dziennych, ale można je stosować dla predykcji wykraczających poza 1 rok naprzód. Niemniej, okresowo trzeba będzie uaktualniać albo cały biuletyn albo tylko trzy stałe występujące w przytoczonej wyżej formule. Szczególnie ważne będzie uaktualnienie każdorazowo po wystąpieniu sekundy przestępnej. Uwzględnianie poprawki UT1–UTC w Systemie Sterowania sprowadzałoby się do obliczania kąta godzinnego, a zatem czasu gwiazdowego, w oparciu o UT1, a nie jak to czynimy obecnie, o UTC.

Błędy wynikające z dyskretności tabeli poprawek (co dwa stopnie w obu współrzędnych) okazują się zasadniczo niegroźne nawet dla obserwacji na 30 GHz, gdyż aż do wysokości 86° (od 24) nad horyzontem nie przekraczają 0.002°, co ilustruje rysunek Fig. 7.

Pokazane na tym rysunku maksymalne błędy zostały obliczone dla węzłów siatki współrzędnych (azymut i wysokość) odpowiadającej parzystym wartościom tych współrzędnych wyrażonych w stopniach. W sąsiedztwie takich węzłów błędy są największe, gdyż do sterowania brane są wartości poprawek wzięte z węzłów nieparzystych. Do sporządzenia załączonego wykresu wykorzystano obliczenia różnicy w poprawkach wziętych z pełnego modelu i tych z tablicy w czterech punktach bliskich każdego węzła. Punkty te to ±0.00001° w obu współrzędnych wokół węzła. Błędy zdefiniowano jako pierwiastek z sumy kwadratów różnic w obu współrzędnych. Do wykresu zostały wzięte tylko największe wartości tak obliczonych błędów na danej wysokości (odległości zenitalnej).

— KMB        
29 kwietnia 2005 r. (ostatnia modyfikacja 2005.05.06)