Analizy przeprowadzone kilka lat wcześniej dotyczyły uproszczonego modelu radioteleskopu RT32, który nie uwzględniał przesłaniania apertury przez słupy i ramiona konstrukcji wsporczej lustra wtórnego. W tej pracy wykorzytano macierze 1024×1024 punktów ucyfrowionego rysunku czaszy z cieniami (tu jest przykład takiego rysunku z cieniami geometrycznymi). Czarnobiałe rysunki tego rodzaju były konwertowane na format 'raw' a następnie piksele czytane jako binarne dane zero-jedynkowe. Uzyskane tak dane były z kolei przemnażane przez funkcję oświetlenia i transformowane zwykłym (nie szybkim) przekształceniem Fouriera na widmo przestrzenne. Użytą procedurę (DFTxy) dyskretnej dwuwymiarowej transformaty Fouriera zawiera ramka poniżej.

subroutine DFTxy(x,y,daneRe,daneIm,N,u,v,DFT_Re,DFT_Im) c Procedura oblicza jeden punkt zespolonego dwuwymiarowego widma c Fouriera (DFT_Re,DFT_Im) funkcji zespolonej reprezentowanej przez c tablice x i y (wspolrzedne) oraz daneRe i daneIm (wartosci funkcji), c wszystkie o wymiarach N. Czestosci przestrzenne u i v sa wyrazone w c liczbie okresow albo cykli (Fu i Fv) na przedziale danych (Dx i Dy) c podzielonej przez te przedzialy: u=Fu/Dx i v=Fv/Dy. Liczy sie tak: c Suma{(daneRe + j*daneIm)*exp[-2*pi*j*(u*x + v*y)]} c gdzie j jest jednostka urojona, a sumowanie przebiega po wszystkich c danych (N). Te sume ewentualnie mozna podzielic, dla znormalizowania, c przez pierwiastek z liczby danych, N, tj. sqrt(N). Te procedure mozna c uzyc do obliczania jednowymiarowej transformaty wolajac ja tak: c call DFTxy(x,y,daneRe,daneIm,N,u,0.d0,DFT_Re,DFT_Im) c gdzie tablica y moze zawierac dowolne wartosci. c Transformate odwrotna dostaniemy zmieniajac znak argumentow u i v: c call DFTxy(x,y,daneRe,daneIm,N,-u,-v,DFT_Re,DFT_Im) implicit real*8 (a-h,o-z) dimension x(N),y(*),daneRe(N),daneIm(N) data dwaPi/6.283185307180d0/ DFT_Re = 0 DFT_Im = 0 do 1 i = 1,N faza = dwaPi*(u*x(i)+v*y(i)) ! u=Fu/Dx ; v=Fv/Dy si=dsin(faza) co=dcos(faza) DFT_Re = DFT_Re + (daneRe(i)*co+daneIm(i)*si) 1 DFT_Im = DFT_Im - (daneRe(i)*si-daneIm(i)*co) end

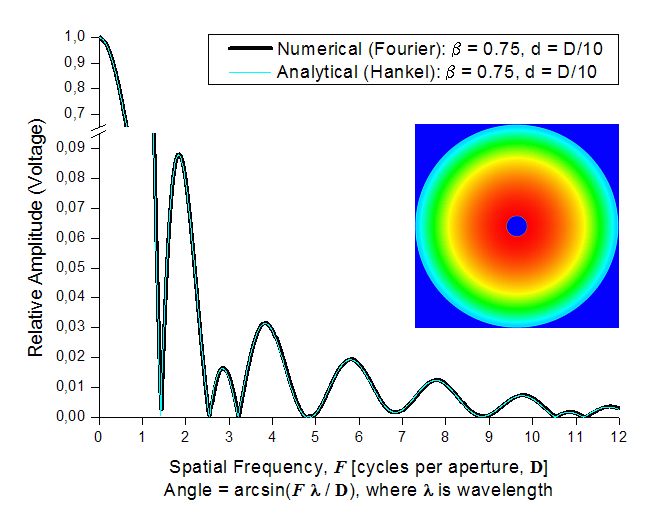
Aby mieć pewność, że schemat ten jest poprawny, przeprowadzono porównanie obliczeń analitycznych dla kołowo symetrycznego modelu RT32 (funkcja CharRT32) i obliczeń za pomocą transformaty Fouriera tegoż modelu w ucyfrowionej postaci (tablica 1024×1024 punktów). Wyniki przedstawia Rys. 1. Jak z niego widać, obie metody dają praktycznie takie same wyniki.

Rys. 1. Przekrój przez widmo przestrzenne dla kołowej apertury o średnicy D z otworem o średnicy d = 0.1 D. Przyjęto rozkład pola w postaci 1 – β(2 r/D)2, gdzie β = 0.75, zaś r to odległość od środka apertury. Oznacza to, że osłabienie oświetlenia czaszy na brzegu (dla r = D/2) względem jej środka wynosi 20 log(1 – β) = –12 dB. Krzywa wykreślona grubą czarną kreską została obliczona za pomocą transformacji Fouriera danych dyskretnych w postaci tablicy o wymiarach 1024×1024, które odpowiadają rysunkowi pokazanemu nad krzywymi. Cieńsza krzywa zaznaczona jasnym kolorem na tle czarnej krzywej to wynik obliczeń analitycznych — jest to transformata Hankela. Pierwszy listek boczny tej charakterystyki ma maksimum na częstości przestrzennej F = 1.83478, co na częstotliwości radiowej 5 GHz (λ = 0.06 m) i dla D = 32 m odpowiada kątowi arcsin(Fλ/D) = 0.1971° = 11.8' liczonemu od kierunku głównej wiązki.

Rys. 2. Rozkład pola na aperturze RT32 w postaci funkcji Gaussa z uwzględnieniem cieni od lustra wtórnego i jego konstrukcji nośnej. Poziomice zaznaczono co 0.1 amplitudy pola przypadającego na środek apertury. Tutaj cienie od konstrukcji nośnej są poszerzone o 5 cm z obu stron poszczególnych elementów konstrukcji. Widmo tego rozkładu pokazano w dolnej części Rys. 4 oraz na Rys. 5. (Uwaga: ten i większość z dalszych rysunków na tej stronie ma większą rozdzielczość niż pokazana; można więc zobaczyć więcej szczegółów po pobraniu pliku danego rysunku.)

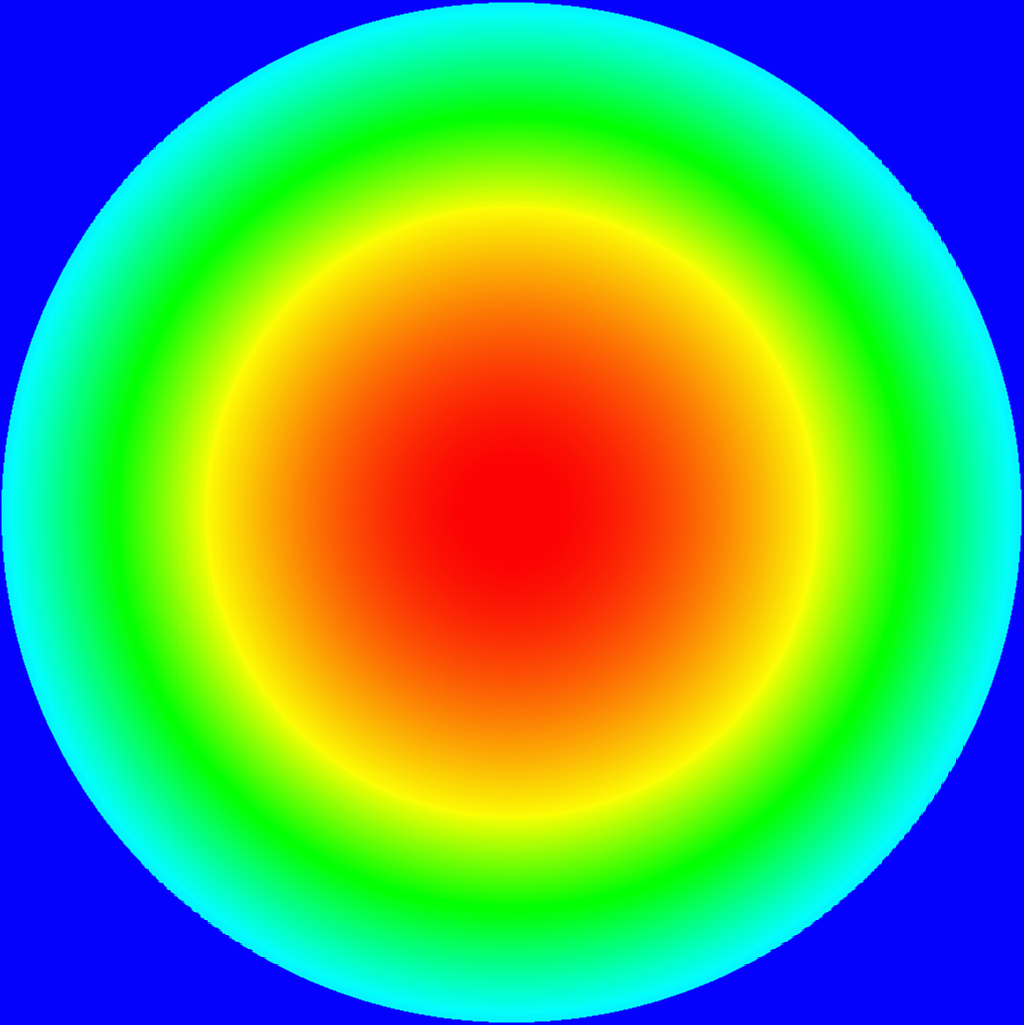
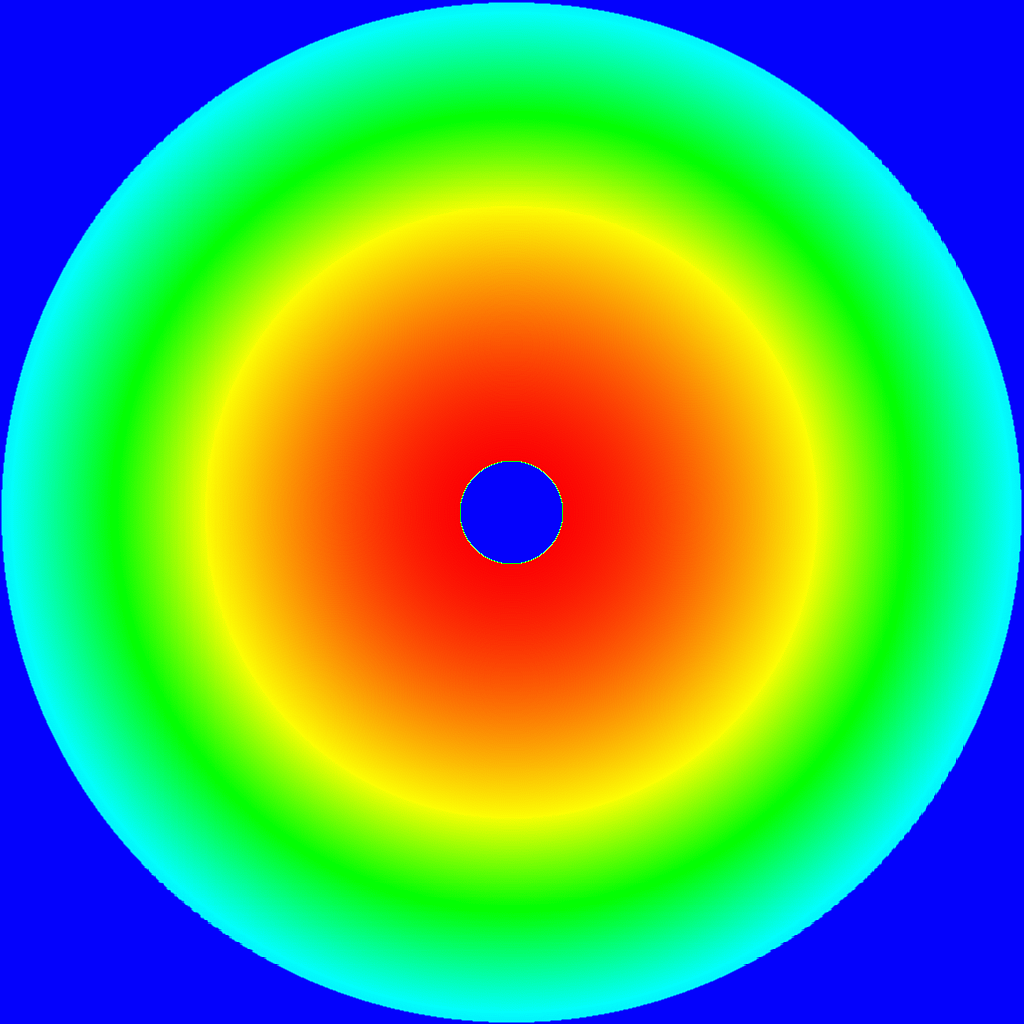
Rys. 3. Gaussowskie rozkłady pola na dysku i dysku z otworem z 10-decybelowym taperem (osłabieniem mocy na brzegach) oraz ich widma. Lewe panele: rozkład pola elektrycznego, u góry – na pełnej aperturze kołowej, u dołu – na aperturze z cieniem subreflektora o średnicy 0.1 głównego lustra. Prawy panel: kompozycja widm przestrzennych – dopełniające się połówki (górna dla częstości przestrzennych [w cyklach na średnicy] 0 < v < 24 i dolna –24 < v < 0) transformat Fouriera (tj. napięciowych charakterystyk kierunkowych) odpowiadajacych rozkładów pola na aperturze, pokazanych w lewych panelach. Mapy wyskalowanie są dla zakresu amplitud od 0 (kolor ciemnoniebieski) do 0.03 i więcej (czerwony). Znaczy to, że w kierunkach wyrysowanych kolorem czerwonym odbierana moc wynosi od 0.0009 do 1 (w środku). Na rozkładach pola skala napięć jest inna: od 0 (na niebiesko) do 1 (na czerwono).

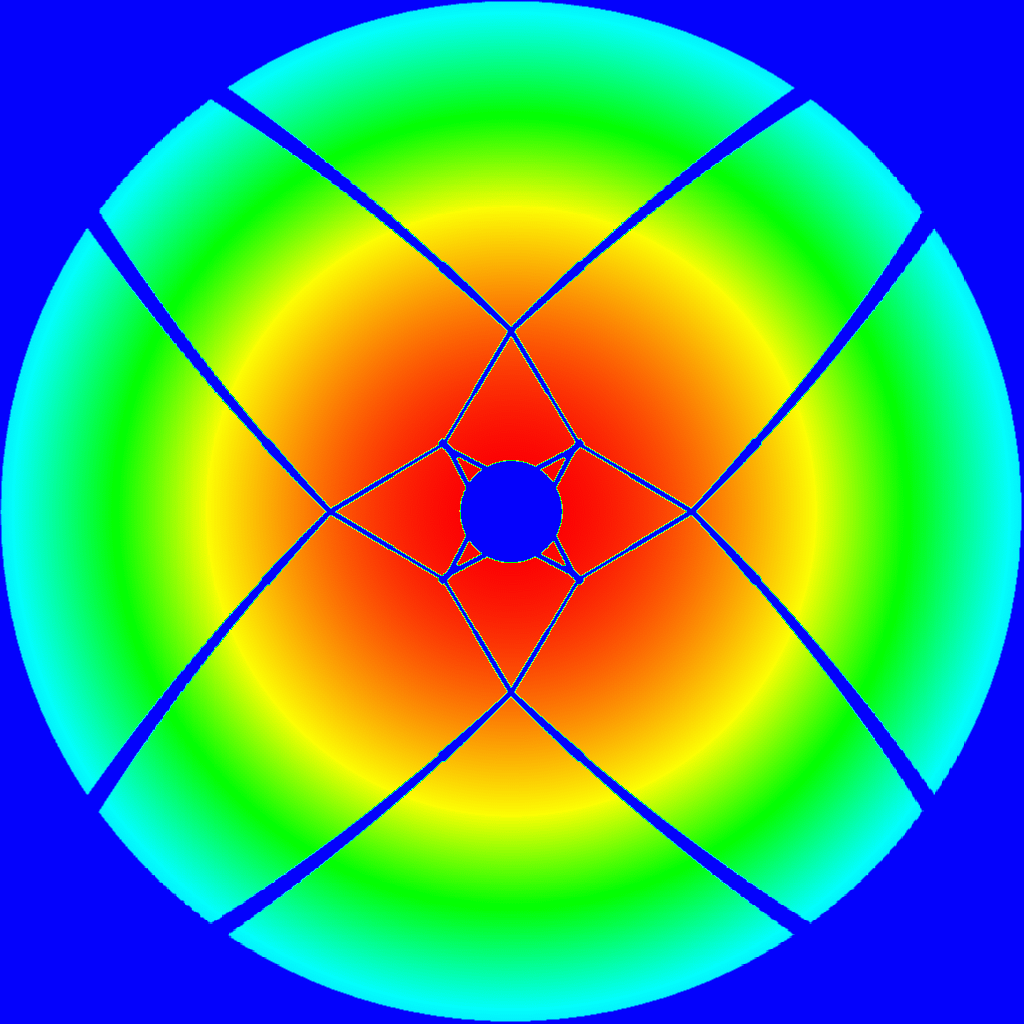
Rys. 4. Rozkład pola i widma RT32 oświetlonego gaussowsko (z 10-decybelowym taperem) z zaznaczonymi cieniami subreflektora i jego konstrukcji wsporczej. Lewe panele: górny – cienie 'optyczne' (geometryczne), dolny – cienie poszerzone o 5 cm z obu stron ramion i słupów (ten sam rozkład w innym rzucie przedstawia Rys. 2). Prawy panel: kompozycja widm przestrzennych – dopełniające się połówki (górna dla częstości przestrzennych [w cyklach na średnicy] 0 < v < 24 i dolna –24 < v < 0) transformat Fouriera (charakterystyk kierunkowych) odpowiadających rozkładów pola na aperturze, pokazanych w lewych panelach. Obie mapy wyskalowanie są dla zakresu od 0 (kolor ciemnoniebieski) do 0.03 i więcej (czerwony). Znaczy to, że w kierunkach wyrysowanych kolorem czerwonym odbierana moc wynosi od 0.0009 do 1 (w środku). Na rozkładach pola (lewe panele) skala napięć jest inna: od 0 (na niebiesko) do 1 (na czerwono).

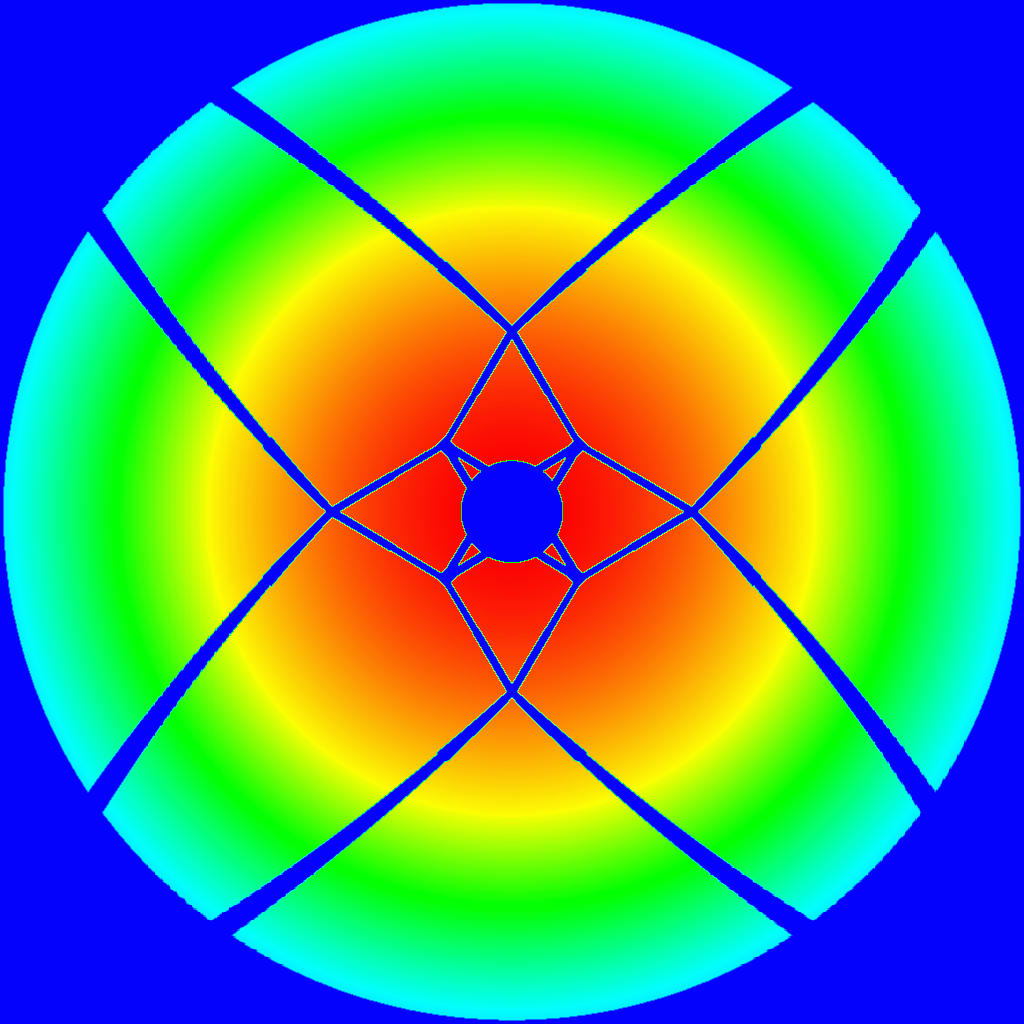
Rys. 5. Struktura listków bocznych napięciowej charakterystyki kierunkowej z dolnej części Rys. 4 w zakresie od 0 do 0.03 wartości w maksimum. Poziomice zaznaczono co 0.003 (najwyższa, kolor czarny, odpowiada poziomowi 0.03, do którego większe amplitudy zostały obcięte).

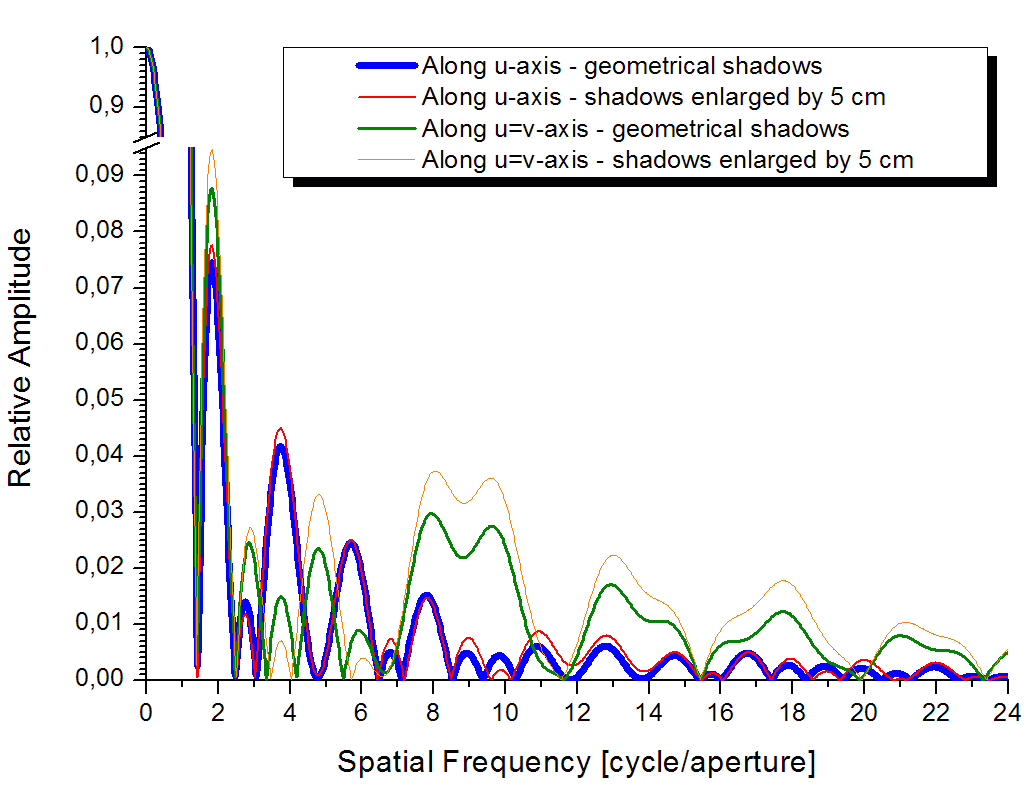
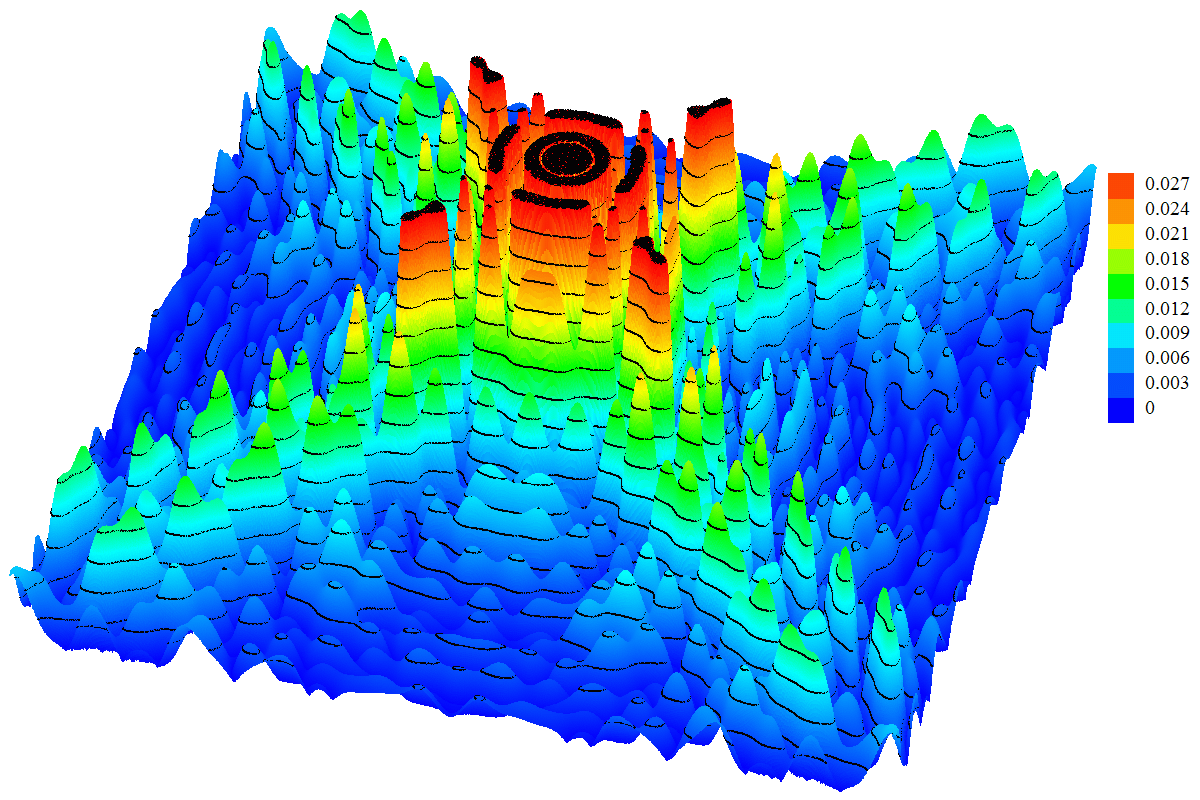
Rys. 6. Przekrój przez listki boczne napięciowych charakterystyk kierunkowych z Rys. 4 na kierunku współrzędnej u (poziomo) i pod kątem 45° do niego.

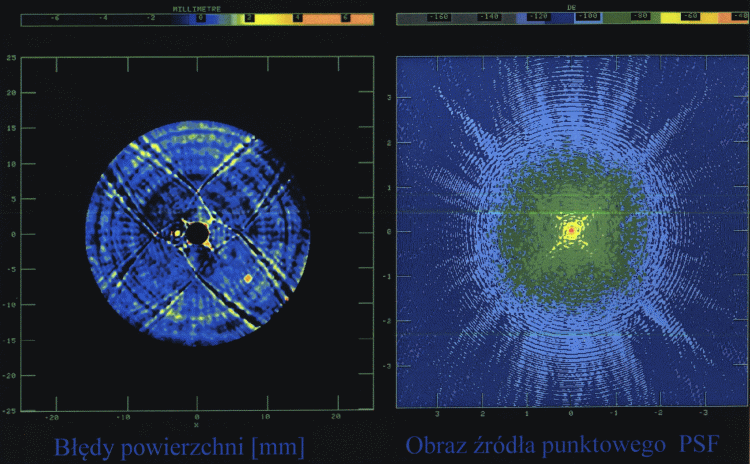
Rys. 7. Wyniki pomiarów holograficznych RT32 na częstotliwości 12 GHz: błędy powierzchni (z lewej) i odpowiednia charakterystyka kierunkowa (z prawej). W charakterystyce kierunkowej zwraca uwagę obecność promienistych struktur wychodzących od wiązki głównej pod kątem 45° względem pionu/poziomu, przypominających te widoczne na Rys. 4 i 5. Rysunek ten obliczył i wykonał Prof. Andrzej Kus.

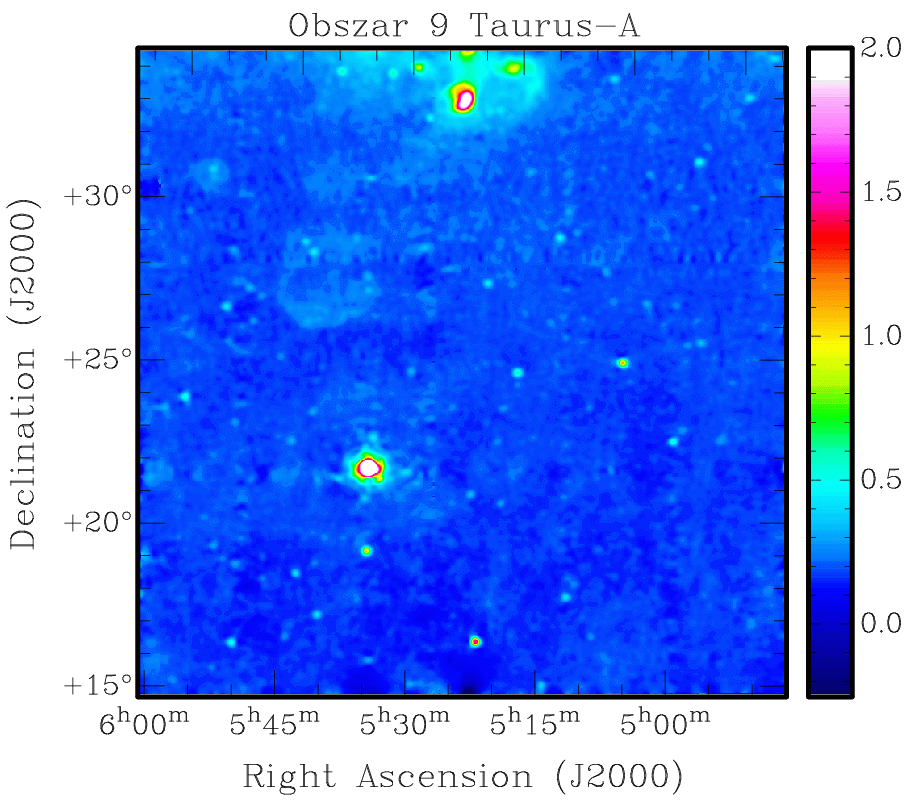
Rys. 8. Mapa okolic źródła Taurus A (Mgławica Krab) uzyskana z obserwacji na fali 6 cm (5 GHz) wzięta z pracy Promieniowanie radiowe (λ = 6 cm) z obszaru antycentrum Galaktyki (autorzy: S. Ryś, E. Pazderski i M. Soida). Wysunięto podejrzenie, że za cztery (trzy?) punktowe źródła dość symetrycznie rozłożone wokół Tau A mogą być odpowiedzialne listki boczne charakterystyki promieniowania RT32. Z tej mapy wynika, że źródła te są odległe o ok. 1° od Kraba, a to przekłada się na sin1° D/λ = 9 cykli częstości przestrzennej. Na Rys. 6 widać, że w zakresie 8–10 cykli rzeczywiście jest dość silny podwójny pik na kierunkach pod kątem 45° względem horyzontu lub wertykału (dla charakterystyki z Rys. 9. ten garbaty pik ma jeszcze większą wysokość: 0.042 i 0.041, gdy na Rys. 6 mamy 0.037 i 0.036 dla ok. 8.1 i 9.6 cykli, odpowiednio). A ponieważ większość obserwacji wykorzystanych do zrobienia tej mapy wykonano kilka godzin (ok. 3) po górowaniu (tj. przy kącie paralaktycznym bliskim 40°, co oznacza taki sam obrót osi u i v charakterystyki względem współrzędnych z mapy), ta hipoteza pochodzenia tych źródeł zyskuje stąd pewne wsparcie.

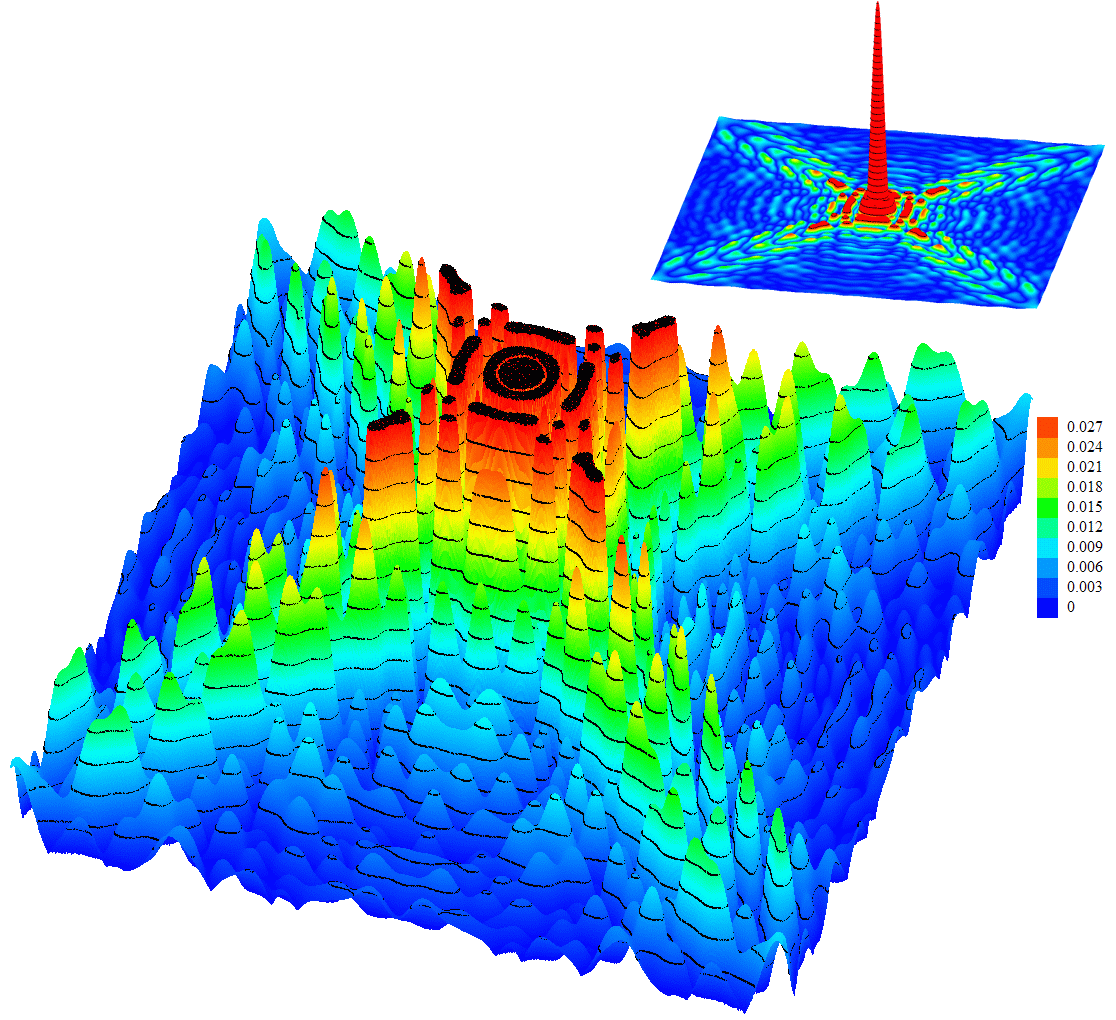
Rys. 9. Struktura napięciowej charakterystyki kierunkowej dla apertury RT32 zacienionej subeflektorem i elementami konstrukcji powiększonymi o 5 cm. Skala i poziomice tej mapy są takie same jak podano w podpisie do Rys. 5. Z prawej strony u góry jest pomniejszona mapka pełnego zakresu charakterystyki w tej samej skali kolorów, ale poziomice są tam co 0.03 (pierwsza poziomica odpowiada więc ostatniej, czyli zaczernionemu poziomowi obcięcia, na głównej mapie).

Wyniki przedstawione poniżej uzyskano tak samo jak dla RT32, ale z tylko czterema prostymi podporami o grubości 0.159 m (tak jak w dolnej części podpór RT32) zamocowanymi u dołu tak samo (tj. przebijającymi czaszę w odległości ok. 5.7 m od osi) ale leżącymi w płaszczyżnie osi paraboloidy, tworząc z tą osią kąt 27.56°.

Rys. 10. Apertura z zaznaczonymi cieniami subreflektora i jego konstrukcji wsporczej i widma przestrzenne (charakterystyki promieniowania) teleskopu oświetlonego gaussowsko (z 10-decybelowym taperem). Lewe panele: górny – cienie 'optyczne' (geometryczne), dolny – cienie od nóg wsporczych i subreflektora o promieniach powiększonych o 5 cm. Prawy panel: kompozycja widm przestrzennych – dopełniające się połówki (górna dla częstości przestrzennych [w cyklach na średnicy] 0 < v < 24 i dolna –24 < v < 0) transformat Fouriera (charakterystyk kierunkowych) odpowiadających rozkładów pola na aperturze, pokazanych w lewych panelach. Obie mapy wyskalowane są tak samo jak na Rys. 4. Znaczy to, że w kierunkach wyrysowanych kolorem czerwonym odbierana moc przekracza 0.0009 wartości w maksimum (tj. tej w środku). Ten kwadratowy obszar na fali λ = 6 cm skaluje się na niebie jako pole o bokach 2 arcsin(24*0.06/32) = 2.58°. Trójwymiarową mapę dla dolnego przypadku zawiera następny rysunek.

Rys. 11. Struktura napięciowej charakterystyki kierunkowej dla apertury hipotetycznego RT32 zacienionej subeflektorem i 4 prostymi jego podporami powiększonymi w promieniu o 5 cm w stosunku do założonych z lewego górnego panelu na Rys. 10. Skala kolorów tej mapy jest taka sama jak na Rys. 5 i Rys. 9, tzn. od 0 (na niebiesko) do 0.03 (na czerwono), a poziomice zaznaczono co 0.003 (najwyższa, kolor czarny, odpowiada poziomowi 0.03, do którego większe amplitudy zostały obcięte). Z prawej strony u góry jest pomniejszona mapka pełnego zakresu charakterystyki w tej samej skali kolorów, ale poziomice są tam co 0.03 (pierwsza poziomica odpowiada więc ostatniej, czyli czarnemu poziomowi obcięcia, na głównej mapie).

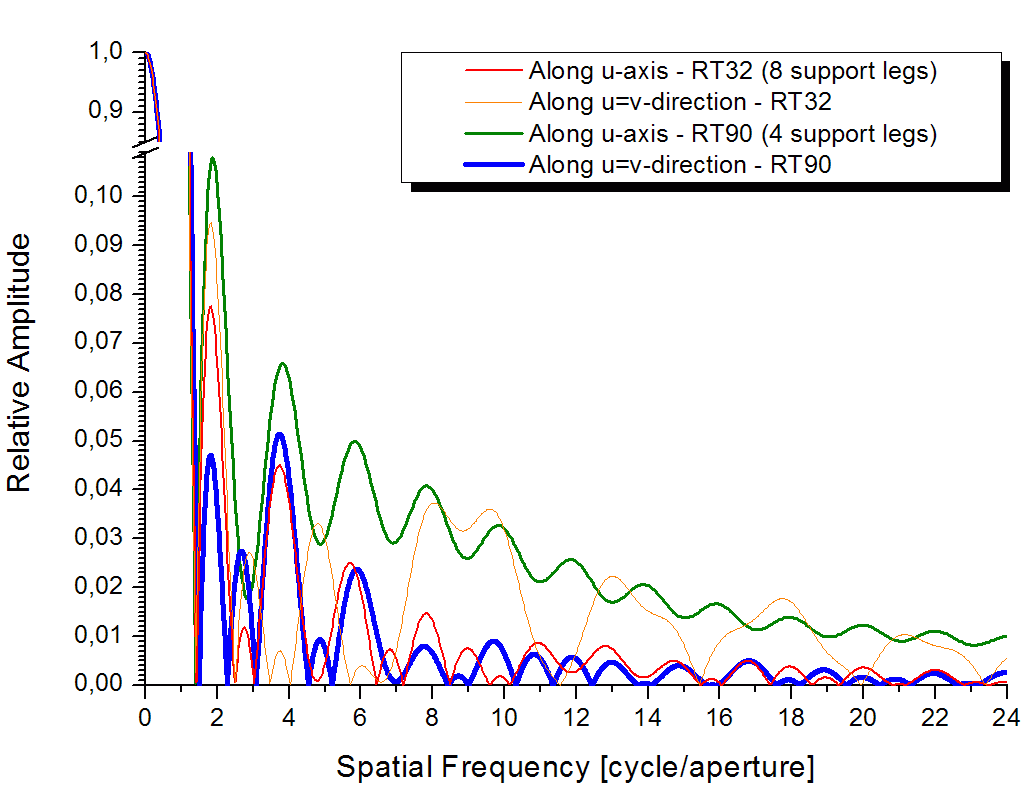
Rys. 12. Przekroje przez listki boczne napięciowych charakterystyk kierunkowych z Rys. 5 i Rys. 11 na kierunku współrzędnej u (lub v, tj. poziomo lub po wertykale) i pod kątem 45° do niego. Krzywe czerwona i żółta są tymi samymi, co na Rys. 6 (tj. dla RT32), zaś zielona i niebieska odpowiadają radioteleskopowi o podobnej geometrii, ale z bardziej typowym zawieszeniem subreflektora, na 4 podporach. Wszystkie przedstawione tu przypadki dotyczą cieni od subreflektora i elementów konstrukcji wsporczych powiększonych o 10 cm na średnicach lub szerokościach.

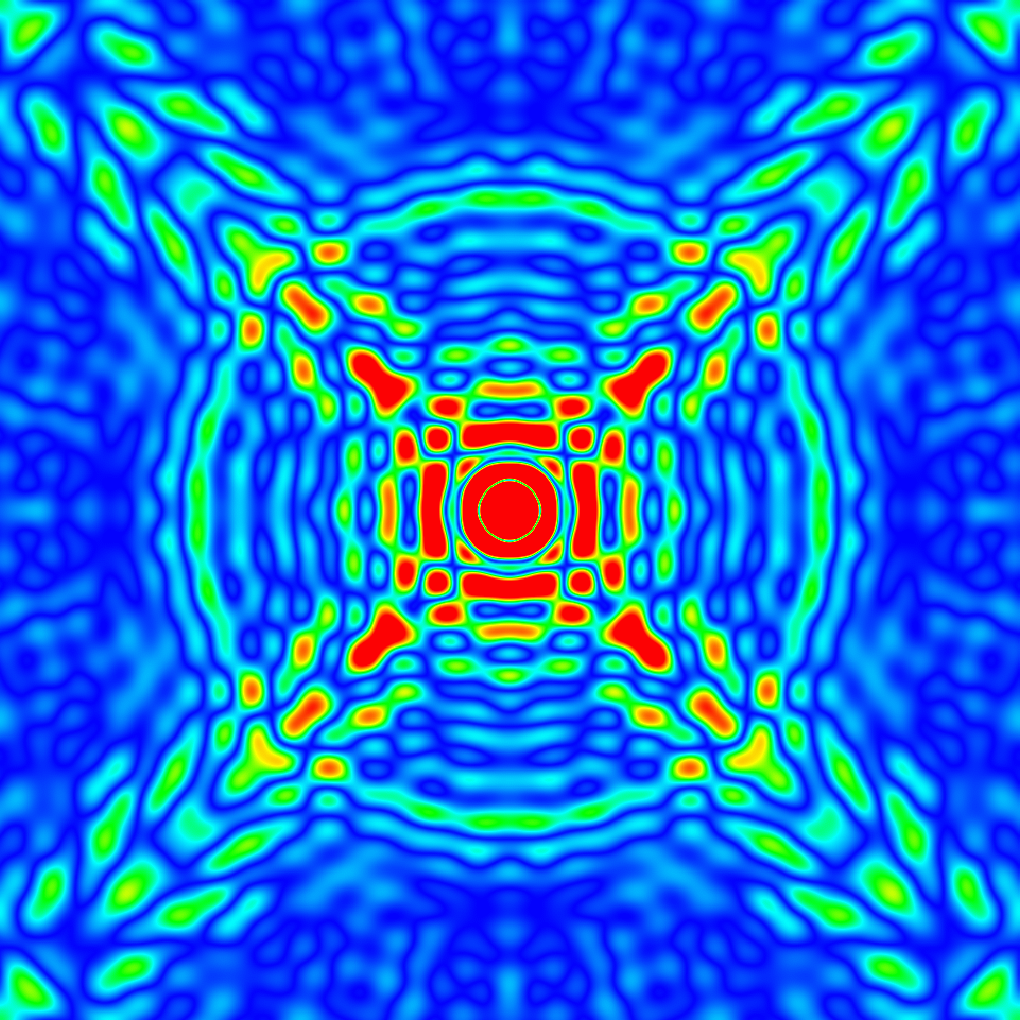
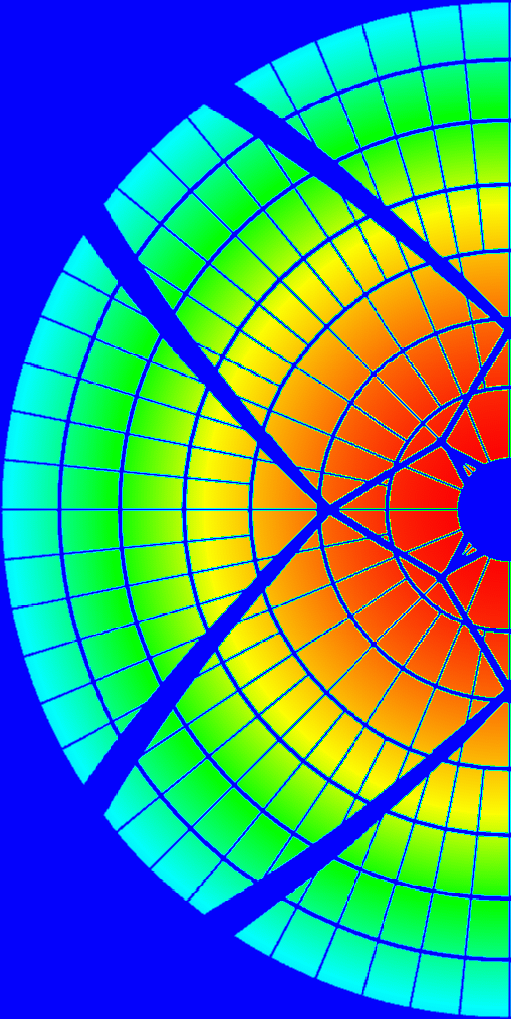
Rys. 13. Lewy panel: połowa apertury RT32 z zaznaczonymi panelami głównego reflektora oraz cieniami powiększonego o 5 cm subreflektora i jego konstrukcji wsporczej. Tutaj szpary między pierścieniami paneli mają szerokość ok. 5 pikseli (przy średnicy czaszy ok. 1020 pikseli przekłada się to na prawie 16 cm na faktycznej aperturze), zaś te radialne były rysowane kreską dwukrotnie cieńszą. Kolory oznaczają amplitudę pola elektrycznego w postaci funkcji Gaussa (z 10-decybelowym taperem), od 0 (kolor niebieski) do 1 (czerwony). Prawy panel: mapa amplitudy widma przestrzennego (charakterystyki promieniowania) tego teleskopu w zakresie ±24 cykli na aperturze w obu współrzędnych. Mapa wyskalowana jest tak samo jak na wcześniejszych rysunkach, tzn. od 0 (kolor niebieski) do 0.03 i więcej (kolor czerwony).

KMB, Toruń–Piwnice, dn. 23 lipca 2012 r.