Pointing and RT32 Gain
| •
Model3
has an azimuth component of –0.013255°/sin(z) ↓
Radiation pattern deviates to the right by 0.013°Subreflector is translated –0.013255/–3.3925 m = +4 mm to the left (as seen from the feeds) → 1.5 % ABERRATION LOSSES ——— or ——— is rotated by –0.013255°/0.1046 = –0.127° (i.e., seen from feeds, its vertex to the right) around prime focus → NO LOSSES• Data of campaign 2003 against 2004 shifted in azimuth by –0.017° → translation of secondary by 5 mm (direction being consistent with the idea that the above 4 mm is purely due to it) |
The losses of about 1.5 % resulting from the translation in case
of RT32 cannot be compensated by other subreflector motions.
|
Conclusion: a small (4 –
5 mm) correction in the horizontal position of the Cassegrain mirror
promises the recovery of about 12 m2 of aperture area
(5 panels) supposedly lost
at 30 GHz after unintentional change
during maintenance of the mirror drives in 2003. The pronounced asymmetry
of the first side lobe (seen in the above figure) should be observable
provided the signal to noise ratio exceeding 50:1 can be achieved for a point source.
If observationally detected it would be rather unmistakable indication of the presence
of discussed lateral misalignment of the secondary.
In fact similar signature on the first
sidelobe could be expected also of a feed displacement, however to get comparable
magnitude of the distortion it would require as much as a metre of its lateral offset
and another nearly 0.5 m of axial adjustment.
Pointing Model Revisited
Alarmingly large percentage (Roman Feiler) of pointing errors in measurements made between 30 March and 7 April 2005 with OCRA crossed the level of 0.01° (half of HPBW at 30 GHz):
17 % of 314 measurements in the azimuth coordinate
36 % of 314 measurements in the zenith distance
After correction for variable astronomical effects of the annual aberration of light and nutation of Earth axis (see these figures) these numbers reduce to:
8 % in the azimuth
23 % in the zenith distance
This makes average of 14 % of real 'outliers'.
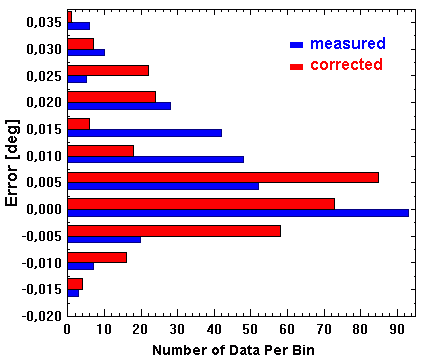
Of original data (of 2003 and 2004) used to fit the pointing model (the one currently used)
|
|
The above figure shows that in the zenith distance coordinate there is considerable fraction (about 15 %) of errors in the range +0.0175 to +0.0275°. Attributing them all to the +0.02-degree jump diminishes those 23 % to 8 %, about equal to the other coordinate percentage.
Thus, after correction for the two variable astronomical
effects and the jump in elevation coordinate this new series of measurements
appears to contain only about 8 % 'outliers'. This favourably compares with
the mentioned 11 % of similar outliers in the original data of 2003/2004.
The missed 3 % can easily be explained by preselection effects
(data analysed here have been picked, by RF, from a larger set with an eye on
'better' measurements).
Conclusion 1: Analysed measurements confirm that Model3 developed last year for RT32 pointing does not contain significant biases.
Conclusion 2: There is an urgent necessity to improve the present steering system in that at least two variable, but easily predictable, astronomical effects (annual aberration and nutation) be accounted for in addition to the precession of catalogue equatorial coordinates of sources when observed with the OCRA receivers.
A further 2 or 3 % improvement in this regard may be expected from inclusion
of the third of most prominent effects, that due to the UT1 – UTC difference.
Practical suggestions on implementation of these effects are given in an
earlier report.
The zenith distance coordinate pointing apparently
is still very much affected by the 0.02° jump.
Can Model3 be improved?
|
Pointing Lookup Table
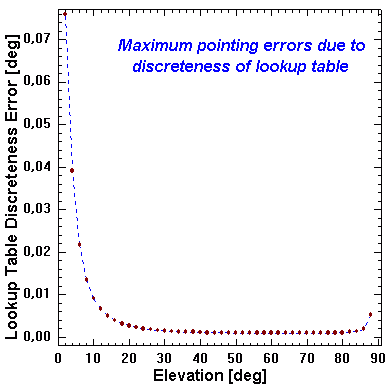
Corrections of nominal coordinates presently are done every 2° of azimuth and zenith distance using lookup table data at odd number of degrees of the coordinates.
No interpolation:
The plot below shows the largest value of position errors (composed of errors in the two coordinates added quadratically) of all knots at each even degree of elevation starting from the telescope horizon (i.e. elevation of 2°).
|
Between altitudes 24 and 86° this pointing error does not exceed 0.002°, and falls below 0.001° for altitudes 50 to 78°.
Conclusion: Anccuracy of current scheme of using lookup table for pointing corrections seems satisfactory for OCRA purposes.
More on Optical Properties
The results presented in the following figures were obtained with the help of OptiCass program set so that the ray tracing was being performed for 1300 rays and power spectrum computed at 625 points evenly distributed in the u×v window of 5×5 (i.e. over a spherical square of about 5 HPBW on a side, or ±2.5 beamwidths around the main lobe).
The gain losses represent the percentage of the beam peak power that gets lost when phase errors due to ray path lengths are accounted for. The parabolic illumination function was assumed, with 12 dB edge taper. Diffraction effects were neglected altogether (other calculation indicates that the RT32 gain loss due to diffraction at the secondary at this wavelength is about 1.65 %).

| |
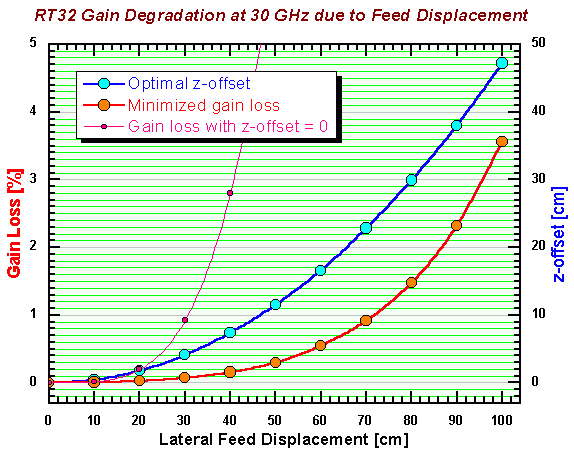
| RT32 aperture efficiency losses due to subreflector lateral displacement and defocus of subreflector and feeds. Note the different scale (top) for the subreflector displacements. Downward axial displacements result in similar (although slightly smaller) losses as these presented | |
| An error of 1 mm in the axial position of the subreflector results in similar gain losses (1.4 %) as these due to 50 mm of the feed axial displacement (1.3 %)! |
Is this observation consistent with the known fact that the secondary focus is of the order of the magnification squared, M2, as deep as the prime focus? Typically the proportionality factor in this rule is estimated to about 0.7 and M of RT32 equals to about 8.7, thus the theoretical ratio of the two depths would be about 53. This number is in very good agreement with the above noted factor of 50. The purpose of this check is to convince the reader that the presented results, though obtained with entirely new software (the OptiCass program), can be relied upon. There are more checks available for inspection in another document. Those there are related to various beam parameters (such as the width and deviations in response to feed and subreflector offsets).
To arrive at the optimized results for lateral feed offsets use was made of the OptiCass 'o' (optimize) command. The command causes two searches: first for minimum of aberration losses as a function of the z-coordinate of feeds, and then for minimum of 'total losses' (accounting for the spillover and the illumination function) as a function of the feed radiation pattern direction in the plane containing the telescope optical axis (z-axis) and the displaced feed. The displacement of this pattern with respect to the nominal direction (towards the centre of subreflector) matches roughly a linear law of 0.7° per metre of the lateral feed offset in the direction opposite to the beam squint (i.e. so that the rays shifted closer to the dish rim get slightly diminished weight).
| |
|
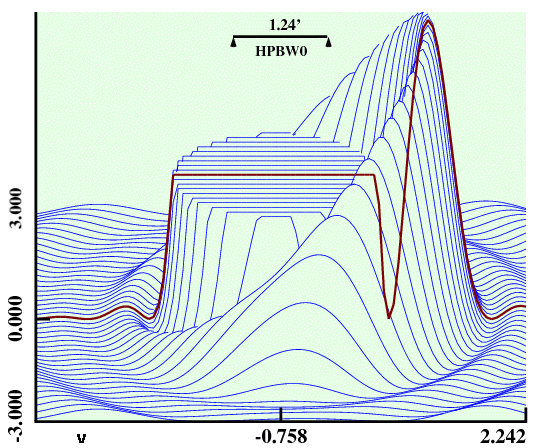
Wavefront aberration losses in antenna gain as a function of
lateral displacement of feeds computed for the RT32 optics and observing
frequency of 30 GHz. The thinner
pink curve shows the losses with feeds kept
at the level of nominal focal plane, i.e. without refocusing, while the thick
red curve (lowest one) represents the minimum loss when
the feed z-coordinate and its direction of radiation pattern are adjusted.
The amount of the refocussing required is shown as the
blue curve.
Numerical values of losses at the smallest displacement plotted (10 cm) are
0.017 % (without z-offset) and 0.006 % (z-offset of 4.5 mm)
| |
| For lateral feed displacements smaller than 10 cm, even in the absence of refocusing, the aberration losses are negligible (staying below 0.02 %). |
Postscript: OCRA-F Losses
| The material in this section is a fruit of informal discussions and computations carried out during the Workshop and only later has been added to this document. |
Next generation of the OCRA array is expected to have 16 closely packed feeds placed at the same height (z-coordinate). Each horn (8.5 cm in diameter) will be directed parallelly to z-axis. This means that the outermost and innermost feeds will be displaced by 18 cm and 6 cm, respectively, from the RT32 optical axis.
OptiCass computes patterns assuming the feed to be directed towards the subreflector centre, but a user can offset this direction as he desires. Making the feed radiation pattern parallel to z-axis in OptiCass is particularly simple since one of normally displayed parameters is the inclination of the feed — subreflector centre direction with respect to the optical axis. Thus it is enough to set one of the two feed angles to the value displayed for the corresponding inclination angle assigning to it an opposite sign. This procedure was used to compute results that follow.
OCRA5 ====> r-offset: max = 0.18 m, min = 0.06 m
Feed pattern parallel to optical axis
Feed Beam Aberr Spill 1st side
z-off angle squint loss loss lobe
m deg deg % % %
Outer feeds, r_off = 18 cm
0.0 -1.1275 -0.1057 0.1344 0.2834 0.8634 <== Feed toward subrefl. centre
0.0 0.0 -0.1058 0.1128 0.1973 0.8636 <== Feed parallel to z
0.014 -0.0017 -0.1059 0.0192 0.1976 0.8770 <== Optimal z-offset
0.014 0.0000 -0.1059 0.0192 0.1975 0.8771 <== Parallel to z (final)
Inner feeds, r_off = 6 cm
0.0 -0.3759 -0.0352 0.0035 0.0847 0.7672 <== Subreflector centre
0.0 0.0 -0.0352 0.0033 0.0752 0.7686 <== Parallel to z
0.002 0.0 -0.0353 0.0021 0.0752 0.7692 <== Optimal position
Aberration and added-spillover losses for all the feeds at the same
level (z-off, counted from the secondary focus, upwards positive)
Feed at r=6cm Feed at r=13.44cm Feed at r=18cm
z-off Aberr Spill Aberr Spill Aberr Spill
m % % % % % %
0.008 0.0233 0.0753 0.0108 0.1432 0.0357 0.1974
0.009 0.0304 0.0753 0.0115 0.1432 0.0305 0.1974 <== 'best z'
0.010 0.0386 0.0753 0.0133 0.1432 0.0263 0.1975
Complete set of assumed and computed parameters
as displayed by OptiCass for the outer feed at optimal z
SETTABLE parameters # #0 #1 #2 #3 #4
Cassegrain: D,X_min,f,Xs_max,h2 [m] 0 32.000 -16.000 11.200 1.600 1.000
Subreflector: x,y,z, tx, ty [m,deg] 1 0.000 0.000 0.000 0.000 0.000
Feed offsets: x,y,z, Dtx,Dty [m,deg] 2 0.180 0.000 0.009 1.129 0.000
Ray-tracing: N/R.NxNy,Nu,Nv,maxU,maxV 3 20.00 24. 24. 2.500 2.500
Wavel,Taper,zAprt,pltD,pivot [m,dB,-] 4 0.010 12.000 -8.343 2. -1.
COMPUTED param's & x,z_piv,du,v,N 0.000 0.480 0.004 0.000 0.000
Main dish: f/D,f/Dp, D2, G,coordG [m] 6 0.3500 0.3500 32.000 5.714 16.000
angles: t_V,t_H, t_0, t_1, t_2 [deg] 7 142.151 142.151 0.000 -71.075 71.075
Subreflector: Dc,Dm,Ds2,Gs,Xs_min [m] 8 3.2000 3.2000 3.2000 0.5056 -1.6000
feed angles: t_VH,t_c,_0,_1,_2 [deg] 9 18.8256 0.0000 0.0000 -9.4128 9.4128
Cassegrain: f1, f2, fs, F, M [m,-] 10 1.0541 9.1459 10.2000 97.173 8.6762
Hyperbola: a,c,b,e, FSAmpRatio [m,-] 11 4.0459 5.1000 3.1050 1.2605 0.9933
Beam: t_u,t_v, HPBW_u,_v,_0 [deg] 12 -0.1058 0.0000 0.0210 0.0206 0.0208
Squint, phi_X,Y, apert_X,Y [deg,m] 13 0.1058 -1.1286 0.0000 -0.1999 0.0000
Loss: Aberr,Spill,A&S,IllDec,Totl [%] 14 0.0305 0.1974 0.2279 3.0697 3.2905
pathR,ComaLow,-Hi,1stLob,Totl'[m,%] 15 0.0575 -0.0799 1.5544 0.8715 1.232
|
Note in the above tables the same (in absolute sense) values for feed initial direction to the subreflector centre (phi_X of –1.1286) and feed radiation pattern offset (Dtx of 1.129, which is internal 1.1286 rounded only for display). This ensures parallelism of the feed pattern and the RT32 optical axis.
| These computations demonstrate that for the OCRA-F size the losses due to lateral feed displacements and due to the field curvature will not be significant. If the array is placed exactly in the focal plane, the aberration losses (i.e. those usually referred to as coma and astigmatism) will not exceed 0.15 % for the outer feeds (the inner feeds will then experience practically no losses). Lifting the array by about 9 mm above the secondary focus, toward the subreflector, nearly equates the losses for the inner and outer feeds (keeping all the 16 feeds still at marginally low losses of about 0.03 % or less). |
Note also: 30 GHz ray-tracing beam of a laterally offset
feed deviates from the RT32 optical axis by 35.3' per metre of offset or
by 21.2" with each centimetre of the offset. Thus the horn separation of
8.5 cm will correspond to 3', or 0.05°, or 2.4 HPBW separation of
beams on the sky.
— KMB
(kb@astro.uni.torun.pl)
Last updated 2005.07.05
.gif)
.gif)
-compare.gif)