Geometria paneli RT32
Kazimierz Borkowski
TRAO
Paraboliczny reflektor radioteleskopu
32-metrowego (zobacz też ten dokument) składa
się z 336 paneli ułożonych w siedmiu koncentrycznych pierścieniach.
Pierścienie mają szerokość 224 cm i taką też długość mają panele,
ich szerokości są zaś różne w różnych pierścieniach.
Wykładzina paneli, stanowiąca powierzchnię odbijającą promieniowanie,
powinna mieć kształt możliwie najbliższy wycinkowi paraboloidy
obrotowej odpowiadającemu danemu pierścieniowi. Zarówno podczas
produkcji paneli, jak i do celów weryfikacji okresowych pomiarów,
potrzebny był i jest matematyczny model powierzchni paneli w układzie
odniesienia związanym z samym panelem, a nie teleskopem jako całością.
Ta strona przedstawia takie modele.
|
Głębokość panelu względem cięciwy |
 |
|
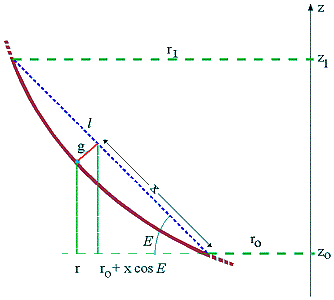
| Rys. 1 |
Rozważmy przekrój paraboloidy radioteleskopu płaszczyzną
przechodzącą przez oś symetrii, z, czaszy (Rys. 1).
Jeśli założymy, że współrzędna z liczona jest od wierzchołka paraboli,
zaś r jest odległością punktu na paraboli od tej osi, to równanie
tej paraboli przyjmie bardzo prostą postać:
gdzie f jest odległością ogniskową paraboli (odległością ogniska
od wierzchołka paraboli) i wynosi 11,2 m.
W przypadku, gdy znamy promienie okręgów ograniczających dany pierścień
paneli, ro i r1, możemy obliczyć kąt, E,
nachylenia cięciwy, która przechodzi przez końce panelu, względem
płaszczyzny apertury (prostopadłej do osi z):
|
tanE = |
z1 − zo
r1 − ro |
= |
r12 −
ro2
4f(r1 − ro) |
|
|
czyli
Długość cięciwy wynosi oczywiście:
Głębokość panelu względem cięciwy w miejscu odległym o r od osi z można
wyrazić przez:
|
g(r) = (r −
ro) sinE −
|
r2 − ro2
4f
|
cosE. | |
(4) |
Stąd da się wyliczyć maksymalną głębokość panelu. Przyrównanie
do zera pochodnej g po r,
daje nam wartość r = 2f tanE, przy której głębokość jest największa
i wynosi:
|
gmax = g(2f tanE)
= (f tanE –
ro) sinE + |
ro2
4f |
cosE. | |
(5) |
W praktyce przydatniejsze jest wyrażenie głębokości w funkcji odległości,
x, mierzonej wzdłuż cięciwy, poczynając od końca panelu bliższego
osi teleskopu. Eliminując r z układu
-
r = ro + x cosE + g sinE
r2 = ro2 + 4f(x sinE
− g cosE)
i otrzymane równanie rozwiązując ze względu na g, nietrudno dowieść, że
|
g(x) = |
|
√4f x/sinE
+ C2 |
− C − x cosE |
sinE |
, | |
| (6) |
gdzie C = ro + 2f/tanE. Analogicznie jak w przypadku
zależności g od r, z tej postaci możemy także wyznaczyć maksymalną
głębokość panelu. Mianowicie, przypada ona na
|
xmax = |
f
sinE cos2E
|
− |
C2sinE
4f |
|
| (7) |
i wynosi
|
gmax = |
(f/sinE − 0,5C cosE)2
f cosE |
. |
| (8) |
To wyrażenie jest, oczywiście, równoważne równaniu (5).
|
Wpływ odkształcenia panelu na fazę
sygnału |
 |
|
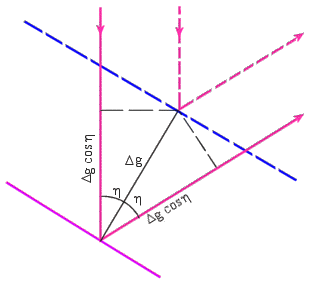
| Rys. 2 |
Jeżeli głębokość panelu w miejscu odległym o r od osi paraboloidu
jest większa od projektowanej o Δg,
wówczas zarówno promień padający, jak i odbity, mają drogę dłuższą
od spodziewanej o Δg cosη (Rys. 2),
gdzie η jest kątem nachylenia stycznej
do paraboli w tym miejscu, czyli
|
η = arctan |
r
2f |
= arccos[ |
1/√{
|
1 + |
(
|
0,5r/f
)2 |
| }] |
|
(kąt E, jak widać z porównania z (2), jest
równy η dla średniej wartości skrajnych
promieni danego panelu). Zatem przy obserwacjach na fali o długości
λ zmiana fazy sygnału (opóźnienie, czyli
zmniejszenie wartości, przy wgłębieniu na panelu) wyniesie:
|
ΔΦ = 2π |
2Δg cosη
λ
|
= |
8πf
|
· |
Δg
λ |
[rad]. |
| (9) |
W metodzie holograficznej pomiarów anten otrzymuje się rozkład
błędów fazy na płaszczyźnie apertury, czyli na płaszczyźnie
prostopadłej do osi z. Tak więc, jeśli zmierzony błąd fazy w
odległości r od środka apertury można przypisać wyłącznie
niedokładności powierzchni reflektora głównego, wówczas można
zeń wyliczyć wartość (i kierunek) odchyłki głębokości w danym
miejscu czaszy z zależności:
Ponieważ, dla teleskopu parabolicznego o średnicy d,
2f = (2f/d)d, w naszym przypadku mamy:
2f = 2×0,35×2d/2 = 1,4 (d/2). We wzorze (10) za
r/(2f) można więc podstawić
praktyczniejszą wielkość: r'/1,4, gdzie r' jest promieniem znormalizowanym,
liczonym od 0,1 (najbardziej wewnętrzny brzeg paneli) do 1,0 (brzeg
całej czaszy). Dla RT32 mamy w takim razie:
|
Δg = λ |
ΔΦ
4π
|
|
√ |
|
=
|
| 0,05684
|
√ |
1,96 + r'2
|
λ ΔΦ | |
, |
|
(11) |
gdzie ΔΦ należy wyrazić w radianach.
Widać stąd, że czynnik skalujący dla λ ΔΦ
zmienia się od 0,0798 (przy r' = 0,1) do 0,0978 (przy r' =1),
czyli o niespełna 23 %.
κ = √{1 + r2/(2f)2}
Nr panelu 0 1 2 3 4 5 6 7
Promień r [m] 16.000 14.143 12.214 10.212 8.141 6.007 3.822 1.600
Współczynnik κ 1.229 1.183 1.139 1.099 1.064 1.035 1.014 1.003
|
|
Radialne odległości paneli |
W obliczeniach związanych z głębokością panelu wymagana jest znajomość
odległości jego brzegów od osi symetrii (ro i r1).
Można je wyznaczyć w oparciu o fakt, że projektowana długość wszystkich
paneli jest taka sama (ok. 2,24 m). Ponieważ nie jest precyzyjnie powiedziane
jak ta długość jest określona, przyjmiemy że jest mierzona po parabolicznym
łuku przekroju panelu (siedem cięciw o wspomnianej długości nie zmieściłoby
się w zadanej geometrii czaszy). Poniżej przedstawimy sposób obliczenia
promieni ri przez podzielenie łuku paraboli na 7 równych odcinków.
Infinitezymalnie mała długość łuku krzywej płaskiej wynosi w ogólności
ds = √{dr2 + dz2}.
W przypadku paraboli opisanej równaniem (1), długość
łuku liczonego od wierzchołka paraboli do odległości r wyrazi się całką:
|
|
|
|
| = |
∫ |
r
0 |
√ |
|
dr = |
∫ |
r
0 |
√ |
|
dr = | |
|
|
|
|
| = |
r
4f
| |
√
|
4f2 + r2
|
+ f·ln |
2f
|
. |
| |
| |
| (12) |
Zatem łuk od wewnętrznej strony wewnętrznego pierścienia paneli, czyli
od odległości r = 1,6 m, do brzegu czaszy (r = 16 m) ma
długość (w metrach):
|
s(16) − s(1,6) = | 17,271731652
− 1,601359505 = |
|
= | 15,670372147 = 7×2,238624592. |
|
Mamy już zatem 6 punktów wzdłuż paraboli, co ok. 2,239 m licząc od brzegu
czaszy, którym należy teraz przypisać odpowiadające im promienie r. Z braku
analitycznego rozwiązania tego zadania, wykorzystano następujący podprogram
(w języku Fortran) dający rozwiązanie numeryczne:
real*8 function RADIUS(sr)
c Oblicza funkcje odwrotna do s(r), tj. promien
c r = radius przy zadanej dlugosci luku paraboli
implicit real*8 (a-h,o-z)
eps = 1d-7
dx = .05d0
x = sr
1 r1 = s(x) - sr
r2 = s(x+dx) - sr
p = (r2 - r1)/dx
x = x - r1/p
if(abs(r1/p).gt.eps) go to 1
radius = x + .5*r1/p
end
|
W poniższej tabeli zebrano ważniejsze parametry
opisujące położenie, rozmiary i kształt paneli poszczególnych pierścieni.
Trzeba pamiętać, że wymiary te zostały tutaj wyliczone dla idealnego
pokrycia apertury; w rzeczywistości panele są mniejsze, gdyż między nimi,
z oczywistych względów, zostawiono kilkumilimetrowe odstępy. Podane w tabeli
pole powierzchni panelu można wyliczyć, podobnie jak długość łuku ze wzoru
(12), przez scałkowanie elementu powierzchni:
2πr ds. Dla symetrycznego wycinka paraboloidy
o promieniu r otrzymuje się:
A(r) = 8πf2{[1 +
(0,5r/f)2]3/2 – 1}/3.
Pole pojedynczego panelu z pierścienia zawierającego N paneli wynosi więc:
AN = [A(rout) – A(rin)]/N,
gdzie wskaźniki out i in odróżniają promienie zewnętrznych i
wewnętrznych, odpowiednio, boków panelu.
| Tabela 1. Parametry paneli RT32 |
|
Wszystkie wielkości o wymiarze długości
podano tu w milimetrach (kąty 2P, rozwarcia paneli, E,
nachylenia cięciwy, i E', nachylenia płaszczyzny odniesienia, są wyrażone
w stopniach). 'Łuk' jest odległością od wewnętrznego brzegu
lustra mierzoną, inaczej niż promienie r, po powierzchni paneli. Parametr
z'out jest wysokością ponad wewnętrzny brzeg lustra.
Yout, Yin i l są długościami boków rombu
wyznaczonego przez narożniki panelu, Dlug to wysokość tego rombu
(panel po stronie zewnętrznej wystaje poza romb o
'+' i jest wcięty od wewnątrz na
'-') zaś A jest polem (na paraboloidzie) panelu.
G... są głębokościami panelu względem płaszczyzny przechodzącej
przez jego narożniki: Gmax — maksymalną całego panelu,
Gout — na środku między zewnętrznymi narożnikami,
Gin — między wewnętrznymi narożnikami. Wiersze zaczynające
się od liczb (od 100 do 2200) zawierają głębokości g(x) (tj. względem
cięciwy) paneli co 100 mm w x liczonym od wewnętrznego końca cięciwy;
jej maksymalna wartość wynosi gmax = g(xmax). W ostatnim
wierszu parametr Δx wskazuje przybliżone położenie
(względem teoretycznego brzegu panelu) pierwszego rzędu z siatki pomiarów
przedstawionych w dokumentacji pracy Karola Borkowego (Tab. 2).
|
Pierścień I (1) II (2) III (3) IV (4) V (5) VI (6) VII (7)
N 64 64 64 64 32 32 16
Łuk' 15670.37 13431.75 11193.12 8954.50 6715.87 4477.25 2238.62
rout 16000.00 14142.91 12213.76 10212.36 8141.38 6007.36 3821.53
rin 14142.91 12213.76 10212.36 8141.38 6007.36 3821.53 1600.00
zout 5714.29 4464.77 3329.82 2327.96 1479.51 805.54 325.98
z'out 5657.14 4407.63 3272.68 2270.81 1422.37 748.40 268.84
Yout 1570.17 1387.92 1198.61 1002.20 1595.99 1177.65 1491.09
Yin 1387.92 1198.61 1002.20 798.96 1177.65 749.15 624.29
Dlug 2236.46 2236.24 2236.00 2235.73 2228.12 2227.54 2195.37
+ 15.98 14.68 13.15 11.38 37.37 28.25 72.88
- 14.13 12.68 11.00 9.07 27.57 17.97 30.51
l 2238.32 2238.25 2238.16 2238.04 2237.92 2237.82 2237.74
A [m2] 3.314 2.898 2.466 2.018 3.112 2.162 2.385
2P [°] 5.63 5.63 5.63 5.63 11.25 11.25 22.50
E [°] 33.93 30.47 26.59 22.28 17.53 12.37 6.90
E'[°] 33.97 30.50 26.62 22.30 17.61 12.43 7.03
Gmax 26.11 25.95 26.04 26.34 34.55 31.14 33.77
Gout 11.20 9.10 7.04 5.10 13.38 7.48 12.25
Gin 9.10 7.04 5.10 3.35 7.49 3.09 2.17
gmax 15.97 17.90 19.99 22.16 24.25 26.06 27.36
xmax 1108.50 1108.72 1109.22 1110.15 1111.59 1113.54 1115.94
100.0 2.77 3.11 3.47 3.84 4.19 4.49 4.70
200.0 5.28 5.92 6.60 7.31 7.98 8.55 8.95
300.0 7.52 8.43 9.40 10.41 11.37 12.19 12.76
400.0 9.49 10.64 11.87 13.14 14.36 15.40 16.12
500.0 11.20 12.55 14.01 15.51 16.95 18.18 19.05
600.0 12.64 14.17 15.82 17.52 19.15 20.55 21.53
700.0 13.83 15.50 17.30 19.16 20.95 22.49 23.57
800.0 14.75 16.53 18.46 20.45 22.36 24.01 25.18
900.0 15.41 17.28 19.29 21.37 23.38 25.11 26.34
1000.0 15.82 17.74 19.80 21.94 24.00 25.79 27.07
1100.0 15.97 17.90 19.99 22.15 24.24 26.06 27.35
1200.0 15.86 17.79 19.86 22.01 24.10 25.90 27.21
1300.0 15.50 17.38 19.41 21.52 23.56 25.34 26.62
1400.0 14.89 16.70 18.65 20.68 22.64 24.36 25.60
1500.0 14.03 15.73 17.57 19.48 21.34 22.96 24.14
1600.0 12.92 14.48 16.18 17.94 19.66 21.16 22.25
1700.0 11.55 12.96 14.47 16.05 17.59 18.94 19.93
1800.0 9.95 11.15 12.46 13.82 15.15 16.32 17.18
1900.0 8.09 9.07 10.14 11.25 12.33 13.28 13.99
2000.0 5.99 6.72 7.51 8.33 9.13 9.84 10.37
2100.0 3.65 4.09 4.57 5.07 5.56 6.00 6.32
2200.0 1.06 1.19 1.33 1.47 1.62 1.74 1.84
Δx 58 57 57 56.5 49.1 49 15.5
|
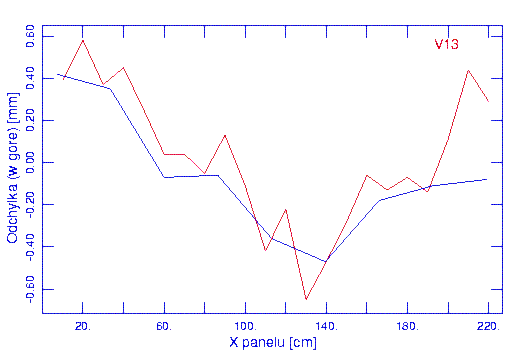
Na Rys. 3. pokazano wyniki pomiarów panelu z pierścienia
V o numerze 13 (numeracja zaczyna się od 1 i, dla patrzącego ze środka
czaszy skierowanej na zenit, biegnie od kierunku południa w lewo) wykonane
w lutym 1993 r. (przez mgr inż. Karola Borkowego), przed montażem
radioteleskopu, (kolor niebieski) i
w październiku 2003 r. (czerwony) wzdłuż cięciwy poprowadzonej przez
środek panelu. Są to odchyłki w górę, w kierunku cięciwy, (gdy są dodatnie)
od modelowej paraboli wyrażone w milimetrach. Jak stąd widać, przez
dziesięć lat ten szczególny panel nie uległ istotnym odkształceniom.
 |
|
| Rys. 3 |
|
Dwuwymiarowa głębokość panelu |
Głębokość opisana w pierwszym punkcie tego dokumentu dotyczyła
przekroju panelu płaszczyzną przechodzącą przez oś symetrii radioteleskopu
i odległości od cięciwy leżącej w tej płaszczyźnie. Wycinek paraboloidy,
którą odwzorowuje panel, jest jednak trójwymiarowy i pełny praktycznie
użyteczny opis kształtu takiej powierzchni wymaga płaszczyzny odniesienia.
W fazie przygotowań do produkcji paneli wykonawcy potrzebowali matematycznego
modelu głębokości paneli jako funkcji jego odległości od płaszczyzny
opartej na czterech narożnikach panelu. Początek pomiaru prostokątnych
współrzędnych na tej płaszczyźnie został ustalony w lewym (patrząc z
góry) zewnętrznym narożniku panelu, jedną z osi zdefiniowano w kierunku
drugiego zewnętrznego narożnika, a drugą — prostopadle do pierwszej
w stronę narożników wewnętrznych.
| Tabela 2 |
|
Fragment dokumentacji Budowa RT–4. Czasza, panele, pomiary. Pierwszy
wiersz danych zawiera surowe pomiary głębokości w poprzek panelu V w pobliżu
(konkretniej, jak podaje Tab. 1,
Δx = 49.1 mm od)
zewnętrznego brzegu (z krokiem 150 mm), w drugim (odróżnionym tutaj kolorem
niebieskim) są wartości teoretyczne obliczone względem płaszczyzny
przechodzącej przez narożniki (ostatnio przeprowadzono
weryfikację tych wartości), a w trzecim
— odchyłki (po uwzględnieniu
różnicy wartości średnich). Dalsze wiersze na tej stronie dokumentacji
zawierają podobne pomiary wykonane w rzędach biegnących w poprzek panelu
równolegle do tych pierwszych w odstępach co 265 mm (tutaj przytoczone są
wyniki z ostaniego, 9-tego, rzędu w pobliżu wewnętrznego brzegu panelu).
Pierwsza odchyłka zmierzona na linii przechodzącej przez środek (wzdłuż)
panelu (–0.08) została naniesiona na Rys. 3. jako
ostatni pomiar, zaś ostatnia (0.42) — jako pierwszy.
|
Panel V-13
0.00 4.35 7.55 9.95 11.45 11.85 11.35 9.85 7.60 4.40 -0.10
3.50 7.75 11.06 13.43 14.85 15.32 14.85 13.43 11.06 7.75 3.50
0.00 -0.11 -0.01 -0.05 -0.14 -0.08 -0.06 0.01 -0.12 -0.24 0.00
................................................................
0.05 2.25 3.60 4.05 3.50 2.15 0.15
0.00 2.41 5.81 8.24 9.69 10.18 9.69 8.24 5.81 2.41 0.00
0.00 0.25 0.36 0.42 0.50 0.41 0.00
|
Obecne pomiary na czaszy radioteleskopu są odnoszone do wewnętrznego
skraju panelu.
Poniższy podprogram jest zmodyfikowaną wersją oryginalnego programu
przygotowanego w fazie projektowania RT32. Modyfikacje dotyczą tylko
początku i kierunku pomiaru wielkości xo oraz wartości danych
początkowych: liczby paneli nj i ich promieni rj, które
nie były wówczas takie same jak obecnie. Niechaj Czytelnik zwróci też
uwagę na to, że w komentarzach wewnątrz tego programu wielkość x
(np. w G(x)) nie jest tą samą, którą używaliśmy wyżej
(odległością wzdłuż cięciwy), lecz liczy się od osi z prostopadle do
niej (oraz do y). Na końcu listingu znajduje się programik
testowy i wynik jego wykonania (w postaci, jaka pojawia się na ekranie).
double precision function PANEL(NRpan,xo,yo)
c Oblicza odleglosc paraboloidalnego panelu od plaszczyzny odniesienia
c opartej na jego naroznikach w funkcji prostokatnych wspolrzednych
c (xo,yo) na tej plaszczyznie. Srodek między wewnetrznymi (blizszymi
c siebie) naroznikami ma wspolrzedne (0,0), os yo biegnie w kierunku
c wewnetrznego naroznika, zas os xo - na zewnatrz. Przy pomiarach
c podczas produkcji paneli xo i yo liczono od zewnetrznego (lewego
c patrzac z gory) naroznika do wewnatrz, co trzeba uwzglednic
c analizujac dokumentacje tamtych pomiarow; by wrocic do tamtego
c schematu wystarczy wybrac alternatywne opcje podane przy etykietach
c 1 i 2. Wielkosci o wymiarze dlugosci (w tym xo, yo i PANEL) sa
c wyrazone w mm. NRpan przyjmuje wartosci od 1 (zewnetrzny pierscien)
c do 7 (najblizej srodka RT32).
c Rownanie paraboloidu z = r**2/c = (x**2 + y**2)/c, gdzie c = 4f
implicit real*8 (a-h,o-z)
dimension rj(0:7),nj(7)
c Zalozenie bardzo waskich paneli (dużej ich liczby, nj) bardzo dobrze
c przybliza przypadek jednowymiarowej glebokosci (wzgledem cieciwy):
c data c/44.8d3/,nj/7*10000/
data c/44.8d3/,nj/4*64,32,32,16/ ! rzeczywisty RT32
c Promienie okregow ograniczajacych pierscienie paneli obliczone przez
c podzielenie luku wzdluz 'poludnika' miedzy r = 1.6 i 16 m na 7
c rownych czesci za pomoca funkcji RADIUS(sr) (patrz tekst glowny)
data rj/16d3,14142.91d0,12213.76d0,10212.36d0,8141.38d0,
* 6007.36d0,3821.53d0,16d2/,NR/0/
if(NRpan.lt.1.or.NRpan.gt.7) then
print*,' Niema panelu o numerze', NRpan,' !!!'
return
endif
if(NR.eq.NRpan) go to 1
NR=NRpan
c odleglosci brzegow (tez naroznikow) paneli od osi paraboloidy [mm]
r0=rj(NRpan)
r1=rj(NRpan-1)
c P - polowa kata rozwarcia panelu = 180stopni/(liczba paneli)
cosP=cos(3.1415926536d0/nj(NRpan))
c Tangens, kosinus i sinus nachylenia panelu wzgl. plaszcz. (x,y),
c tj. plaszczyzny prostopadlej do osi symetrii paraboloidu, z.
tgE=(r0+r1)/(c*cosP)
cosE=1/sqrt(1+tgE*tgE)
sinE=tgE*cosE
dyo=r1*sqrt(1-cosP*cosP)
c Wymiary panelu: odstep zewnetrznych (Yout) i wewnetrznych (Yin)
c naroznikow, odleglosc prostych laczacych zewnetrzne i wewnetrzne
c narozniki (Dlug) oraz najwieksza odleglosc panelu od plaszczyzny
c odniesienia (Gmax)
Dlug=(r1-r0)*sqrt((r0+r1)**2/c/c+cosP**2)
Yin=2*dyo*r0/r1 !tj. Yout*r0/r1
Gmax=(c/4*tgE-r1*cosP)*sinE+r1*r1/c*cosE
write(*,'(a,4(f8.2,a))')' Yout=',2*dyo,' Yin=',Yin,
* ' Dlug=',Dlug,' Glebokosc=',Gmax,' [mm]'
c Powyzszy wzor na glebokosc Gmax uzyskuje sie z zaleznosci odleglosci
c od paraboloidu do plaszczyzny odniesienia w funkcji x i y:
c G(x)=(r1**2-x**2-y**2)/c*cosE-(r1*cosP-x)*sinE
c G'(x)= sinE-2x*cosE/c = 0 --> x_max=tgE*c/2; przy y=0.
c Wspolrzedne (x0,y0) na plaszczyznie odniesienia maja poczatek:
c y0 na osi symetrii panelu, zas x0 liczone od zewnatrz do srodka.
c Konwersja danych wejsciowych zalezy od ich zdefiniowania:
1 x0=Dlug-xo ! gdy xo liczone od wewnatrz na zewnatrz
c 1 x0=xo ! gdy xo liczone z zewnatrz do wewnatrz
2 y0=yo ! gdy yo liczone od srodka panelu
c 2 y0=yo-dyo ! gdy yo liczone od naroznika panelu
c Dla prostej z=z0-x/tgE prostopadlej do plaszczyzny odnies. w punkcie
c (x0,y0), obliczam wartosc z0, tj. z(x=0,y dowolne). W tymze punkcie
c musi byc tez: z=r1**2/c-x0*sinE i x=r1*cosP-x0*cosE, zatem
cE=c/(tgE+tgE)
z0=r1*(r1+2*cE*cosP)/c-x0/sinE
c Prostopadla przebija panel w punkcie (xp,y0,zp) takim, ze:
c zp = (xp**2+y0**2)/c i zp = z0-xp/tgE
c stad (odejmujac stronami): xp**2+c/tgE*xp+y0**2-z0*c = 0
c sqrt(del)/2 = sqrt((c/(2*tgE))**2-(y0*y0-c*z0))
c xp = sqrt(del)/2-c/(2*tgE)
c (rozwiazanie na xp>0). Wspolrzedne punktu na panelu wynosza wiec
xp=sqrt(cE*cE-y0*y0+c*z0)-cE
zp=(xp*xp+y0*y0)/c
c Obliczam odleglosc punktu na panelu od plaszczyzny odniesienia.
c Na plaszcz. odniesienia jest: x=r1*cosP-x0*cosE oraz
c z=r1**2/c-x0*sinE
dx=xp-(r1*cosP-x0*cosE)
dz=zp-(r1*r1/c-x0*sinE)
PANEL=sign(sqrt(dx*dx+dz*dz),dx)
end
======================================================================
Program Test_Panel !sprawdza procedure PANEL
real*8 panel
G=PANEL(5,1000d0,209.18d0)
print*,' Glebokosc panelu Nr 5 w punkcie (1000,209.18):',G
end
-----------------Wynik wykonania powyzszego programu------------------
Yout= 1595.99 Yin= 1177.65 Dlug= 2228.12 Glebokosc= 34.55 [mm]
Glebokosc panelu Nr 5 w punkcie (1000,209.18): 33.0272
|
W związku z nieco mylącymi oznaczeniami w powyższym programie i
różnicami w stosunku do oznaczeń użytych wcześniej w tym dokumencie
poniżej podajemy dodatkowe wyjaśnienia idei rozwiązań
zastosowanych w podprogramie PANEL.
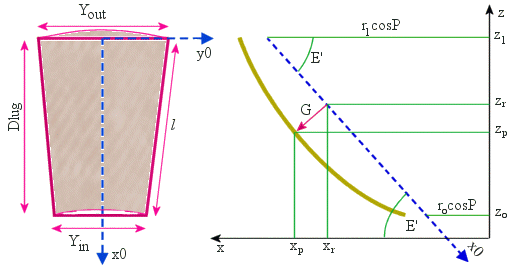 |
|
| Rys. 4 |
W pierścieniach zawierających N paneli, każdy z nich jest ograniczony
płaszczyznami przechodzacymi przez oś paraboloidu i przecinającymi się
pod kątem 2P = 2π/N. Płaszczyzna zawierająca
wszystkie narożniki panelu jest nachylona do płaszczyzny apertury
pod kątem E' takim, że:
tanE' = (r0 + r1)/(4f cosP).
Ten wzór na kąt E' przy znikającym P zmierza do (2).
Romb rozpięty na narożnikach panelu ma wymiary (długości podstaw oraz
wysokość):
| Yout = | 2r1sinP
|
| Yin = | 2r0sinP
|
| Dlug = | r1
– r0
4f
|
√
|
(r0 + r1)2 + (4f cosP)2
|
.
|
Jak widać na Rys. 4, w rzucie na płaszczyznę
odniesienia panel wystaje poza romb i jest nieco wcięty po wewnętrznej
stronie. Łatwo zauważyć, że maksymalna wartość tych odstępstw wynosi:
-
Dlug+ = r1(1 – cosP)cosE' oraz
Dlug– = r0(1 – cosP)cosE',
odpowiednio.
Prosta prostopadła do płaszczyzny odniesienia przechodząca przez punkt
(x0,y0) ma postać:
Punkt (x0,y0) na płaszczyźnie (x,y0,z) spełnia
równania:
-
zr = z0 − xr/tanE',
zr = r12/(4f) − x0 sinE',
xr = r1cosP − x0 cosE'.
Z powyższych trzech równań otrzymujemy stałą do równania prostej
(13):
|
z0 = |
r1
4f
|
(r1 + 4f |
cosP
tanE' |
) − |
x0
sinE' |
. |
|
Prosta (13) przebija paraboloidę (panel) w punkcie
(xp,yp,zp) takim, że
| yp = y0,
zp = |
xp2 + yp2
4f |
,
zp = z0 − |
xp
tanE' |
, |
|
co prowadzi do łatwego do rozwiązania równania:
|
xp2 + |
4f
tanE' |
xp + y02 −
4f z0 = 0. |
|
Otrzymane stąd xp (to z dwóch, które może przyjmować wartości
dodatnie),
xp = √{(2f/tgE')2
– y02 + 4f z0} – 2f/tgE',
pozwala wyliczyć także zp = (xp2
+ y02)/(4f), a więc również
odległość tych dwóch punktów, (xr,y0,zr) i
(xp,y0,zp), jako
|
G(x0,y0) = |
√
|
(xp −
xr)2 + (zp −
zr)2
|
. |
|
Największa głębokość Gmax przypadnie oczywiście gdzieś na
podłużnym przekroju przez środek panelu, tj. dla y0 = 0. Nietrudno
zauważyć, że przy tym warunku
|
G(x) = |
r12 − x2
4f |
cosE' −
(r1cosP − x)sinE',
| | (14) |
co jest analogiczne do (4) i dlatego maksimum ma
także przy x = 2f tanE':
|
Gmax = (f tanE' −
r1cosP)sinE' + |
r12
4f |
cosE'.
| |
Maksymalne głębokości wzdłuż równoległych boków rombu wyznaczonego
przez jego narożniki dostaje się z opisanej procedury
na głębokość panelu: PANEL(NRpan,0d0,0d0) i
PANEL(NRpan,Dlug,0d0).
Można też wyliczyć je ze wzoru (14) podstawiając w nim
za x wyrażenia r1cosP + G sinE' i r0cosP + G sinE'
i rozwiązując otrzymane równania ze względu na G. Np. dla zewnętrznej
podstawy rombu dostaje się w ten sposób:
Gout =
[√{(r1sinP)2
+ C'2} – C']/sinE'
gdzie C' = 2f/tanE' +
r1cosP (na drugiej podstawie mamy taką samą postać
rozwiązania, w którym rolę r1 zastępuje r0).
Te wzory posłużyły do obliczenia odpowiednich składników Tab.
1. Wartości uzyskane procedurą PANEL wywołaną z
argumentami y0 = 0 i x0 = 0 lub x0 = Dlug nie różnią się od podanych w tabeli.
Bardziej kłopotliwe jest wyliczenie maksymalnej głębokości wzdłuż ukośnych
boków rombu. Chociaż ten przypadek nie ma istotnego znaczenia praktycznego,
dla kompletności poniżej przedstawiamy odpowiednie rozwiązanie.
Ogólniejsze od (14) jest równanie:
|
G(x,y) = |
r12 − (x2
+ y2)
4f |
cosE' − (r1cosP − x)sinE',
| | (15) |
w którym x i y wskazują na punkt na paraboloidzie. Dla punktów pod prostą
na płaszczyźnie odniesienia, na której leży ukośny bok rombu, słuszne są
związki:
-
x = r1cosP – x0 cosE' + G sinE' oraz
y = r1sinP – x0 tanψ,
gdzie tanψ = (r1 – r0)sinP/Dlug.
Po podstawieniu ich do wzoru (15) i rozwiązaniu ze względu
na G otrzymujemy:
|
G(x0) = (√{b2 + c} – b +
x0 cosE')/sinE', |
| (16) |
gdzie
-
b = 2f/tanE' + r1cosP
c = x0(2r1sinP tanψ –
x0 tan2ψ – 4f/sinE').
Przyrównanie pochodnej G(x0) po x0 do zera prowadzi do rozwiązania:
- A = 2f/sinE' – r1sinP tanψ
B = 2f/(tan2ψ sinE')
– r1sinP/tanψ
D = 2f/tanE' + r1cosP
c1 = [A2 –
(D cosE)2]/[tan2ψ(tan2ψ +
cos2E')]
x0 = √{B2 – c1} – B
które można wykorzystać w (16), albo wraz z
y0 = r1sinP – x0 tanψ
użyć w ogólnej procedurze na głębokość panelu (np. PANEL).
Oba podejścia dają, naturalnie, identyczne wyniki. Z obliczeń wynika, że
maksymalna głębokość z boku panelu względem płaszczyzny odniesienia
jest praktycznie taka sama (z dokładnością do setnej części milimetra)
jak względem cięciwy, gmax, chociaż przypada
w innym miejscu (odległym nawet o ponad 20 cm od xmax
z Tab. 1).
|
File translated from TEX
by
TTH,
version 3.45 on 09 Nov 2003. |
Ostatnia modyfikacja: 2004.05.22 |