Materiał przedstawiony na specjalistycznym seminarium
Katedry Radioastronomii UMK dnia 9 stycznia 2009 r.

Własności powiększonego RT32

K.M. Borkowski, Centrum Astronomii UMK, Toruń

Spis treści
Geometria radioteleskopu
Geometria czaszy RT32 i RT36
Geometria optyki RT32 i RT36
Geometria dodatkowych paneli
Oświetlenie apertury feedem OCRA
Oświetlenie apertury feedem L-band
Własności RT32 i RT36

Streszczenie: W raporcie tym rozpatruje się pewne podstawowe aspekty rozbudowy istniejącego radioteleskopu o średnicy głównego lustra 32 m związane z powiększeniem tego lustra do 36 m. Powiększenie polegałoby na dołożeniu dodatkowego pierścienia 64 jednakowych paneli. Omówiono własności radioteleskopu przy użyciu istniejących oświetlaczy wskazując na znaczący zysk w skuteczności wykorzystania apertury po ewentualnym przystosowaniu oświetlaczy do powiększonej apertury.

Geometria czaszy, paneli i subreflektora

Geometria czaszy RT32 i RT36

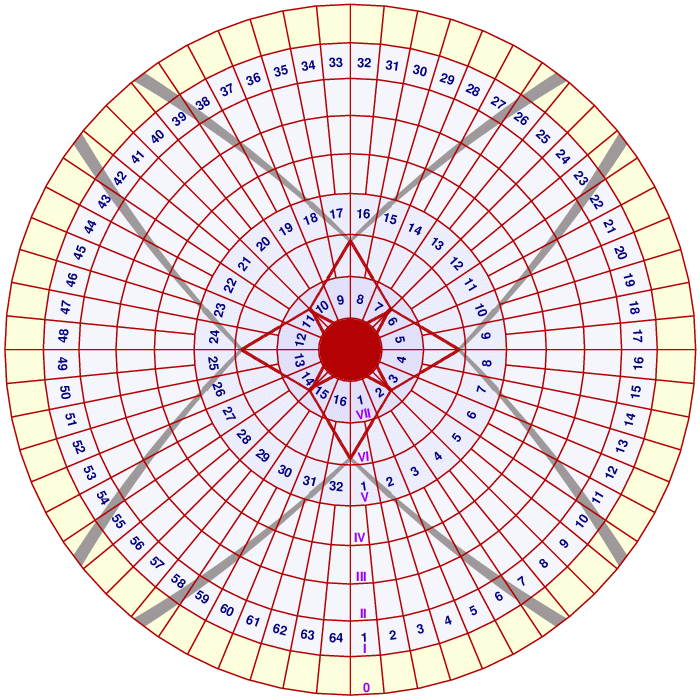
Rozkład paneli i cieni na czaszy rozbudowanego radioteleskopu, RT36, w rzucie na płaszczyznę apertury. Lustro wtórne i elementy jego konstrukcji nośnej przesłaniają promieniowanie padające wprost na czaszę i zostały zaznaczone kolorem czerwonym, natomiast miejsce na lustrze głównym, w którym odbite promienie na drodze do subreflektora trafiają na belki wsporcze zostało zaznaczone na szaro. Numeracja paneli jest zgodna z dokumentacją teleskopu 32-metrowego.

Geometria optyki RT32 i RT36

      Cassegrain radio telescope parameters 
                               
Dish diameter, D                                         32.000    36.000 m
Focal length of primary mirror, f                        11.200           m
Focal ratio of primary mirror, f/D                        0.350     0.311  
Telescope F-number (or F/#): F/D                          3.037     2.699  
Dish depth, g                                             5.714     7.232 m
Dish subtended angle                                    142.151   155.137 deg
Dish edge angle as seen from secondary focus             73.583    70.903 deg
Height of secondary focus above paraboloid vertex, h      1.000           m
Subreflector subtended angle                             18.826    21.166 deg
Subreflector diameter                                     3.200     3.661 m
Diameter of blind area at subreflector centre             0.301     0.345 m
Subreflector depth at centre                              0.506     0.651 m
Subreflector pivot coordinates, x,y,z    0.000   0.000    0.480           m
Prime focus – subreflector edge distance                  1.691     1.874 m
Prime focus to hyperboloid vertex,     f1 = c-a           1.054           m
Secondary focus to hyperboloid vertex, f2 = c+a           9.146           m
Secondary interfocal length, f1+f2 = 2c                  10.200           m
Eccentricity of the hyperboloid, e = c/a                  1.261        
Ray path difference to the foci, (f-h)a/c                 8.092           m
Cassegrain telescope magnification, M = f2/f1             8.676        
Effective focal length, F = M*f                          97.173           m


       Classical optics approximations for Gaussian illumination

Illumination taper at dish edge (OCRA feeds) .......... -11.973  -15.154  dB
Half power beam width (Baars 2003) ....................   0.0208   0.0189 deg
First side lobe power level due to taper (Baars) ......   0.5359   0.4656 %
Gain loss due to tapered illumination .................  13.3106  19.4623 %
Gain loss due to diffraction at subreflector (Lamb) ...   1.6524   1.2288 %
 Coma gain loss due to lateral feed offset ............   0.0008   0.0014 %
 Aberration (astigmatism & coma) gain loss ............   0.0008   0.0014 %
Beam dev. due to primary translation (Baars) ..........  -3.9803  -3.8116 deg/m
Beam dev. due to primary rotation .....................   1.7781   1.7451 deg/deg
Beam dev. due to secondary translation ................  -3.3969  -3.2281 deg/m
Beam dev. due to secondary rotation about vertex ......   0.1664   0.1633 deg/deg
Beam dev. due to secondary rotation about focus .......   0.1039   0.1039 deg/deg
Beam dev. due to secondary rotation about "z_piv" .....   0.0754   0.0768 deg/deg
Beam dev. due to feed translation in secondary focus ..  -0.5834  -0.5835 deg/m
Feed offset per beam width, prime focus (Baars) .......  -0.0052  -0.0050 m
Feed offset per beam width, secondary focus ...........  -0.0357  -0.0324 m

Geometria paneli

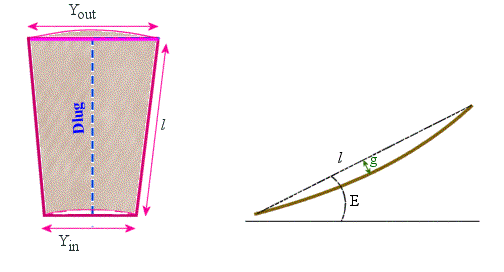
Profil i głębokość panela

Poniższa analiza oparta jest na kompletniejszym opracowaniu .

Równania paraboli tworzącej główny reflektor i hiperboli tworzącej subreflektor mają postać:

z =

r²

(1)

z = a

( √

r²

b²

+ 1

– 1

)

(2)

gdzie współrzędna z liczona jest od wierzchołka paraboli lub hiperboli wzdłuż osi symetrii, r jest odległością punktu na paraboli lub hiperboli od tej osi, f = 11,2 m jest odległością ogniskową paraboli (odległością ogniska od wierzchołka paraboli), zaś a = 4.0459 m i b = √(c² – a²) = 3.1050 m to parametry hiperboli tworzącej subreflektor.

Znając promienie okręgów ograniczających pierścień paneli, r_o = 16 m i r₁ = 18 m, możemy obliczyć kąt nachylenia E oraz długość l cięciwy, która leży w płaszczyźnie osi symetrii czaszy i przechodzi przez końce panela:

E = arctan

(

r_o + r₁

4 f

)

(3)

l =

r₁ – r_o

cos E

(4)

Głębokość panela względem cięciwy wynosi:

g(ξ) =

√

4 f ξ/sin E + C²

– C – ξcos E

sin E

(5)

gdzie ξ jest mierzone wzdłuż cięciwy od jej końca bliższego osi paraboloidy, a C = r_o + 2 f / tan E. Głebokość ta osiąga największa wartość

g_max =

(f / sin E – 0.5 C cos E)²

f cos E

(6)

dla

ξ_max =

sin E cos²E

–

C²sin E

4 f

(7)

W fazie przygotowań do produkcji paneli wykonawcy będą potrzebowali matematycznego modelu głębokości paneli jako funkcji jego odległości od płaszczyzny opartej na czterech narożnikach panela. Taki model wraz z programem zawiera ten dokument. Można w nim znaleźć też inne zależności, potrzebne do obliczenia długości po łuku łuk i trójwymiarowej powierzchni paneli jako wycinka paraboloidy(A).

W poniższej tabeli zebrano ważniejsze parametry opisujące położenie i kształt paneli poszczególnych rzędów. Wszystkie liczby podano tam w milimetrach, z wyjątkiem kątów E i E′, które wyrażono w stopniach (E′ jest analogicznym do omówionego nachylenia cięciwy E nachyleniem wspomnianej wyżej płaszczyzny odniesienia względem płaszczyzny apertury). Końcowe wiersze tabeli zaczynające się od liczb ξ (od 100 do 2500) zawierają głębokości g(ξ) paneli mierzone w punktach ξ liczonych od wewnętrznego końca cięciwy co 100 mm.

Parametry paneli RT36


Pierścień 0        1        2        3        4        5        6        7

N        64       64       64       64       64       32       32       16
r_1   18000.00 16000.00 14142.91 12213.76 10212.36  8141.38  6007.35  3821.53
z_1    7232.14  5714.29  4464.77  3329.82  2327.96  1479.51   805.54   325.98
l      2510.75  2238.32  2238.24  2238.15  2238.04  2237.92  2237.82  2237.73
łuk    2511.09  2238.62  2238.62  2238.62  2238.62  2238.62  2238.62  2238.62
A [m2]   4.193    3.314    2.898    2.466    2.018    3.112    2.162    2.385
E        37.20    33.93    30.47    26.59    22.28    17.53    12.37     6.90
ξ_max  1241.88  1108.42  1108.59  1109.07  1109.95  1111.31  1113.19  1115.56
g_max    17.78    15.97    17.90    19.99    22.15    24.23    26.04    27.34
       Parametry mierzone na płaszczyźnie odniesienia lub względem niej
Yout   1766.44  1570.17  1387.92  1198.61  1002.20  1595.99  1177.65  1491.09
Yin    1570.17  1387.92  1198.61  1002.20   798.96  1177.65   749.15   624.29
Gmax     30.17    26.11    25.95    26.04    26.34    34.55    31.14    33.77
E'       37.23    33.97    30.50    26.62    22.30    17.61    12.43     7.03
Dlug   2508.84  2236.47  2236.19  2236.00  2235.77  2228.13  2227.53  2195.37
   +     17.26    15.98    14.68    13.15    11.38    37.37    28.25    72.88
   -     15.35    14.13    12.68    11.00     9.07    27.57    17.97    30.51
                   Głębokości mierzone względem cięciwy
 100      2.78     2.77     3.11     3.47     3.84     4.19     4.49     4.69
 200      5.31     5.28     5.92     6.60     7.31     7.98     8.55     8.94
 300      7.61     7.52     8.43     9.40    10.41    11.37    12.18    12.75
 400      9.67     9.49    10.64    11.87    13.14    14.35    15.39    16.12
 500     11.49    11.20    12.55    14.01    15.51    16.95    18.18    19.04
 600     13.08    12.64    14.17    15.82    17.51    19.14    20.54    21.52
 700     14.44    13.83    15.50    17.30    19.16    20.94    22.48    23.56
 800     15.56    14.75    16.53    18.46    20.44    22.35    24.00    25.16
 900     16.45    15.41    17.28    19.29    21.37    23.37    25.10    26.32
1000     17.12    15.82    17.73    19.80    21.93    23.99    25.78    27.05
1100     17.55    15.97    17.90    19.99    22.15    24.23    26.04    27.34
1200     17.76    15.86    17.78    19.86    22.01    24.08    25.89    27.19
1300     17.74    15.50    17.38    19.41    21.51    23.55    25.32    26.60
1400     17.50    14.89    16.69    18.64    20.67    22.63    24.34    25.58
1500     17.03    14.03    15.72    17.56    19.47    21.32    22.94    24.12
1600     16.34    12.91    14.48    16.17    17.93    19.64    21.13    22.23
1700     15.43    11.55    12.95    14.47    16.04    17.57    18.92    19.90
1800     14.30     9.94    11.14    12.45    13.81    15.13    16.29    17.15
1900     12.95     8.09     9.06    10.13    11.23    12.31    13.26    13.96
2000     11.38     5.99     6.71     7.50     8.32     9.11     9.81    10.34
2100      9.59     3.64     4.08     4.56     5.06     5.54     5.97     6.28
2200      7.59     1.06     1.18     1.32     1.46     1.59     1.71     1.80
2300      5.37
2400      2.94
2500      0.30

Przesłanianie paneli przez nogi wsporcze lustra wtórnego

Cień od ośmiu nóg wsporczych subreflectora na panelach pierścienia '0' ma powierzchnię:

8×(7.474 – 5.641) = 1.833×8 = 14.664 m²

i stanowi to ułamek 14.664/(64×4.193) = 0.0228 czyli tylko około 2 % całkowitej powierzchni apertury zewnętrznego pierścienia.
Dla porównania, w RT32 apertura jest blokowana na poziomie ok. 7.4 %

Oświetlenie apertury feedem OCRA

Wszystkie systemy odbiorcze RT32 mają oświetlecze przystosowane do geometrii tego teleskopu, tzn. do optymalnego oświetlenia lustra wtórnego, które widać z ogniska wtórnego pod kątem ok. 18.8°. Rozbudowany teleskop będzie miał większe lustro wtórne, widoczne z feedów pod kątem ok. 21.2 stopnia. Ocenimy jak skutecznie zostanie oświetlona apertura powiększonej czaszy za pomocą obecnego systemu OCRA.

Do dalszych analiz przydatny jest rozkład amplitudy promieniowania oświetlaczy na aperturze. Zmierzoną charakterystykę promieniowania P(θ) = V²(θ) łatwo jest przekształcić na rozkład pola na aperturze korzystając z zależności

r = 2F tan(θ/2),

gdzie r to odległość od środka apertury do punktu na niej, a F – skuteczna ogniskowa systemu Cassegraina.

Najlepsze dopasowanie pomiarów charakterystyki promieniowania oświetlacza OCRA w zakresie r ok. ±18.5 m wokół maksimum do funkcji Gaussa ma postać:

V(r) = e^{–(r –

0.022)²/185.7123} = e^{–[0.073380 (r – 0.022)]²}.

Jest to rozkład pola na aperturze RT32. Ze wzoru tego wynika, że na skraju 32-metrowej czaszy (r = 16) amplituda jest o czynnik 0.252 mniejsza niż w centrum apertury, zatem moc jest mniejsza o ok. 12.0 dB (20 log 0.252). W przypadku powiększonego teleskopu i tego samego rozkładu amplituda na skraju czaszy spada względem kierunku maksimum o czynnik 0.1747 (15.2 dB w mocy).

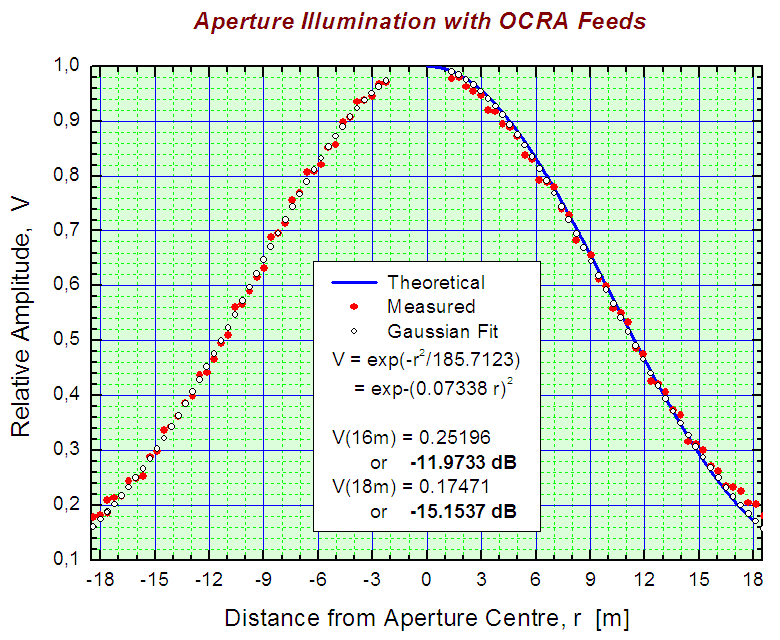
Rozkład amplitud pola promieniowania oświetlaczy OCRA na aperturze RT32. Dane pomiarowe uzyskano z reprezentacji graficznej za pomocą programu WinDig autorstwa Dominique Lovy. Pokazano trzy rozkłady: teoretyczny (krzywa niebieska), zmierzony laboratoryjnie (czerwone punkty) i, kułkami, najlepiej dopasowany do pomiarów rozkład Gaussa (dopasowywano tylko dyspersję i położenie na osi r, przy ustalonej jednostkowej amplitudzie).

Ponieważ nie dysponujemy dokładnymi pomiarami charakterystyk pozostałych oświetlaczy, przy ich analizie posłużymy się obliczeniami teoretycznymi. Większość oświetlaczy RT32 to korugowane anteny piramidalne takiego samego typu jak w systemie OCRA (przeskalowane zgodnie z długością fali) – wszystkie wykonane w Katedrze Radioastronomii. Wykorzystaliśmy algorytm opublikowany przez Loefera i in. (Microwaves, May 1976, p. 58) opisany przez JR Fishera w wewnętrznym raporcie No 190, Electronics Division, NRAO (Green Bank) z września 1978 r. Algorytm ten zapisaliśmy w postać programu w języku Fortran i przetestowaliśmy na przykładzie oświetlacza systemu OCRA. Dla oświetlacza OCRA przyjęliśmy 8 cm na średnicę apertury i długość równą 35 cm. Uzyskana charakterystyka, jak widać na powyższym rysunku, bardzo dobrze zgadza się z wynikami pomiarów: szerokość połówkowa 13.47°, –12.2 dB słabsze oświetlenie skraju czaszy RT32 i –15.3 dB w przypadku RT36.

Do obliczeń przedstawionych niżej dla pozostałych systemów odbiorczych z korugowanymi feedami (takimi nie jest jedynie oświetlacz pasma L) przyjęto, że oświetlenie apertury ma rozkład Gaussa, a na skraju 32-metrowej czaszy jest o 12 dB mniejsze niż w maksimum mocy. Dla anteny powiększonej do 36 m to osłabienie oświetlenie przyjęliśmy na –15.7 dB (ta liczba jest nieco zawyżona; lepiej byłoby przyjąć np. –15.4 dB).

Oświetlenie apertury feedem L-band

W odróżnieniu od pozostałych systemów odbiorczych oświetlacz tubowy na pasmo L jest piramidalnym stożkiem o przekroju kwadratowym. Jego apertura ma wymiary 760 mm × 760 mm, a paszczyzny przeciwległych ścianek przecinają się pod kątem 16.254°. Te parametry można użyć do wyznaczenia charakterystyki promieniowania tego urządzenia na danej długości fali jako transformatę Fouriera z rozkładu pola na aperturze oświetlacza. Zakładając, że czoło fali rozchodzącej się w tubie ma kształt sfery, można obliczyć odchyłki fazy w każdym punkcie apertury względem jej środka i przypisać je zespolonemu rozkładowi pola o stałej amplitudzie. Praktyczne obliczenia wykonaliśmy za pomocą dwuwymiarowego dyskretnego przekształcenia Fouriera (DFT) 21 × 21 jednakowych amplitud i różnych faz w punktach równomiernie rozłożonych na całej płaszczyźnie apertury oświetlacza. Widma obliczano na kwadratowej siatce 62 × 62 nieujemnych punktów płaszczyzny częstości przestrzennych (u,v). Widma te stanowią kierunkową charakterystykę napięciową promieniowania oświetlacza. Poniższy rysunek przedstawia przykład kwadratu takiej charakterystyki (czyli moc promieniowania) dla fali o długości 18 cm.

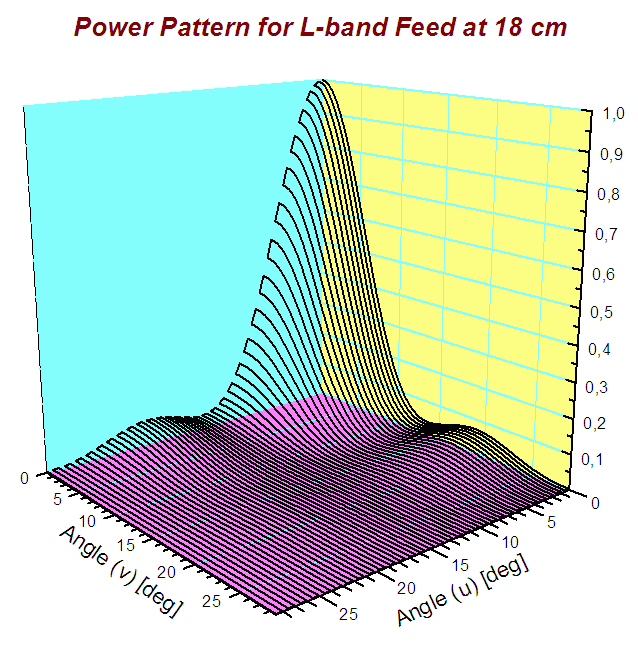
Charakterystyka kierunowa oświetlacza L-band na częstości 1666 MHz (18 cm) obliczona dla sferycznego czoła fali w piramidalnym feedzie. Wykres przedstawia względny rozkład mocy promieniowania (kwadrat amplitudy). Szerokość połówkowa tej charakterystyki wynosi około 12.4° (14.3° dla 21 cm)

Takie charakterystyki zostały przeliczone w postać rozkładów pola na aperturze 32-metrowego radioteleskopu według prostej zależności odległości od środka apertury, r, i kąta charakterystyki (Angle): r = 194.3458 tan(Angle/2), gdzie liczba 194.3458 to podwojona efektywna ogniskowa RT32. Poniższy rysunek przedstawia przykłady tego rodzaju rozkładów dla fali 21 cm.

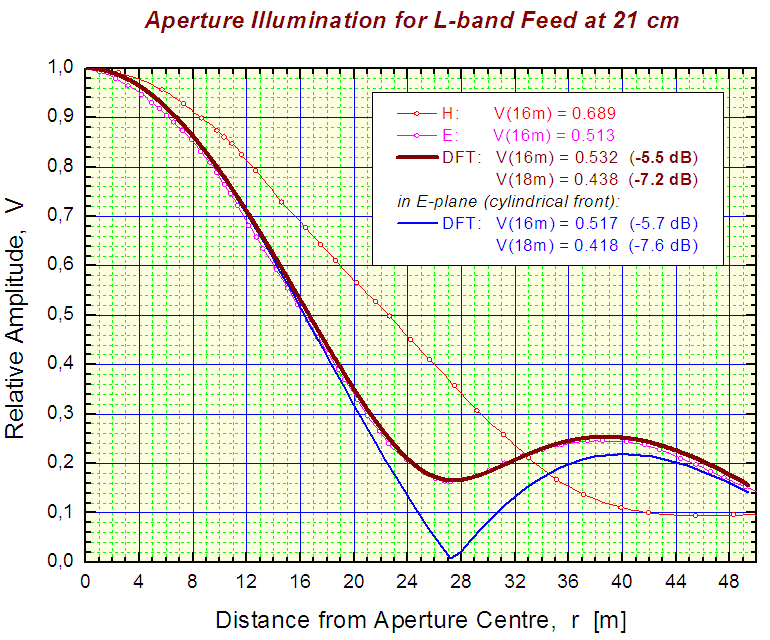
Napięciowy (amplituda) rozkład pola promieniownia oświetlacza L-band na częstości 1420 MHz (21 cm) na aperturze RT32. Dwa przebiegi narysowane krzywymi przerywanymi kółkami są przeskalowanymi wynikami zaczerpniętymi z książki DJ Bema (z użyciem Windig). Odpowiadają one maksymalnemu odchyleniu fazy Ψ_max = π/4, co jest bliskie naszemu oświetlaczowi przy obserwacjach na fali 21 cm (Ψ_max = 0.258 π dla fali 18 cm wartość ta wynosi 0.315 π). Linie ciągłe zostały wyznaczone za pomocą DFT. Są to przekroje rozkładów dwuwymiarowych na kierunku sferycznych odchyłek fazy (krzywa górna, brązowa) i na kierunku stałych odchyłek (cylindryczne czoło fali w piramidalnym feedzie; krzywa dolna, niebieska).

Własności RT32 i RT36

Położenie i własności elektryczne oświetlaczy
Oznaczenia:
λ – długość fali
D – średnica okrągłej lub bok kwadratowej apertury oświetlacza
L – wysokość stożka lub ostrosłupa (piramidy) oświetlacza
Taper32, Taper36 – osłabienie mocy oświetlenia na skraju czaszy RT32 i RT36
x, y, z – odchyłki (wertykalna, horyzontalna i w kierunku subrefl.) feedu od ogniska wtórnego
ΔΘx, ΔΘy – odchyłki (wertykalna i horyzontalna) osi feedu od kierunku na środek subreflektora
Feed λ D L x y z Taper32 Taper36 ΔΘx ΔΘy [cm] [cm] [cm] [cm] [cm] [cm] [dB] [dB] [°] [°]
OCRA 1.0 ~8 ~35 0.0 ±4.25 0.0 -11.973 -15.154 0.000 0.2662 7.3 31
K 1.35 11.7 50 0.0 +66.0 0.0 -12.0 -15.7 0.000 0.000
Kopt* 1.35 11.7 50 0.0 +66.0 +20.2 -12.0 -15.7 0.000 0.000
X1 2.5 19.8 84 +35.04 +65.5 0.0 -12.0 -15.7 0.000 0.000
X2 2.5 19.8 84 +12.03 +65.5 0.0 -12.0 -15.7 0.000 0.000
X3 2.5 19.8 84 -11.99 +65.5 0.0 -12.0 -15.7 0.000 0.000
X4 2.5 19.8 84 -35.01 +65.5 0.0 -12.0 -15.7 0.000 0.000
C2 4.5 33.3 142 +70.24 +29.13 0.0 -12.0 -15.7 0.000 0.000
C1 6.0 43.3 185 +75.9 -25.1 0.0 -12.0 -15.7 0.000 0.000
L-OH 18.0 76.0 266 -84.5 0.0 0.0 -8.54 -11.4 -0.500 0.000 L-H 21.0 76.0 266 -84.5 0.0 0.0 -6.2 -8.4 -0.500 0.000 L-UHF 33.3 76.0 266 -84.5 0.0 0.0 -2.3 -3.0 -0.500 0.000
* Kopt - K z optymalnym podniesieniem ponad płaszczyznę ogniskową

Porównanie parametrów oświetlenia apertury RT32 i RT36
Oznaczenia:
t_u, t_v, Squint – odchyłki (wertykalna, horyzontalna i absolutna) głównej wiązki od osi optycznej RT
HPBW_u, HPBW_v, HPBW_0 – szerokości połówkowe w dwu kierunkach oraz wynik analityczny
Aberr, Spill, IllDec – straty mocy sygnału na skutek aberracji, efektu spillover i ekscentryczności oświetlenia
Total – sumaryczna strata

Feed t_u t_v Squint HPBW_u HPBW_v HPBW_0 phi_X phi_Y Aberr Spill IllDec Total [deg] [deg] [deg] [deg] [deg] [deg] [deg] [deg] [%] [%] [%] [%]
OCRA32 0.0000 -0.0250 0.0250 0.0209 0.0209 0.0208 0.0000 -0.2662 0.0014 0.0995 0.0864 0.1872 36 0.0000 -0.0249 0.0249 0.0192 0.0193 0.0189 0.0000 -0.2662 0.0026 0.0841 0.0678 0.1543
K 32 0.0000 -0.3868 0.3868 0.0286 0.0294 0.0281 0.0000 -4.1275 10.6309 1.6953 0.0000 12.1460 36 0.0000 -0.3865 0.3865 0.0268 0.0277 0.0256 0.0000 -4.1275 15.4898 1.4056 0.0000 16.6776
Kopt32 0.0000 -0.3946 0.3946 0.0284 0.0288 0.0281 0.0000 -4.2204 0.4185 1.8072 0.0000 2.2181 36 0.0000 -0.3942 0.3942 0.0263 0.0267 0.0256 0.0000 -4.2204 0.6883 1.4798 0.0000 2.1579
X1 32 -0.2052 -0.3836 0.4350 0.0530 0.0537 0.0521 -2.1885 -4.0934 5.0337 1.9063 0.0000 6.8440 36 -0.2050 -0.3832 0.4346 0.0494 0.0500 0.0473 -2.1884 -4.0933 7.4299 1.5869 0.0000 8.8989
X2 32 -0.0705 -0.3838 0.3902 0.0527 0.0536 0.0521 -0.7517 -4.0960 3.3159 1.7168 0.0000 4.9758 36 -0.0704 -0.3834 0.3898 0.0490 0.0498 0.0473 -0.7517 -4.0959 4.9184 1.4237 0.0000 6.2721
X3 32 0.0703 -0.3838 0.3902 0.0527 0.0536 0.0521 0.7492 -4.0960 3.3145 1.7167 0.0000 4.9744 36 0.0702 -0.3834 0.3898 0.0490 0.0498 0.0473 0.7492 -4.0959 4.9163 1.4236 0.0000 6.2699
X4 32 0.2050 -0.3836 0.4349 0.0530 0.0537 0.0521 2.1866 -4.0934 5.0293 1.9065 0.0000 6.8400 36 0.2048 -0.3832 0.4345 0.0494 0.0500 0.0473 2.1865 -4.0933 7.4245 1.5867 0.0000 8.8934
C2 32 -0.4113 -0.1706 0.4452 0.0964 0.0951 0.0938 -4.3895 -1.8189 1.7227 1.9708 0.0000 3.6596 36 -0.4108 -0.1704 0.4447 0.0893 0.0883 0.0852 -4.3894 -1.8189 2.5671 1.6291 0.0000 4.1543
C1 32 -0.4443 0.1469 0.4679 0.1286 0.1267 0.1251 -4.7422 1.5667 1.1794 2.0695 0.0000 3.2244 36 -0.4438 0.1469 0.4675 0.1190 0.1175 0.1136 -4.7427 1.5685 1.7596 1.7185 0.0000 3.4478 -12dB -0.4438 0.1469 0.4675 0.1143 0.1126 0.1112 -4.7427 1.5685 1.8531 1.9148 0.0000 3.7325
L18 32 0.4947 0.0000 0.4947 0.3735 0.3652 0.3647 5.2787 0.0000 0.1682 2.3826 -0.1522 2.3985 36 0.4943 0.0000 0.4943 0.3412 0.3349 0.3321 5.2785 0.0000 0.2568 1.8767 -0.1589 1.9732 L21 32 0.4947 0.0000 0.4947 0.4271 0.4167 0.4165 5.2787 0.0000 0.1257 2.8086 -0.1327 2.8021 36 0.4942 0.0000 0.4942 0.3861 0.3779 0.3777 5.2785 0.0000 0.1948 2.2603 -0.1445 2.3098 L33 32 0.4948 0.0000 0.4948 0.6989 0.6843 0.6818 5.2787 0.0000 0.0486 2.2032 -0.1595 2.0948 36 0.4940 0.0000 0.4940 0.5813 0.5655 0.5620 5.2785 0.0000 0.0801 3.7049 -0.0726 3.7122

Powyższa tabela (kolumna 'Total') pokazuje, że straty wynikające z efektów aberracji, spillover i 'niecentralności' oświetlenia wyrażone w procentach głównej wiązki w obu teleskopach są porównywalne. Ponieważ oświetlenie dodatkowej zewnętrznej części apertury RT36 jest 15 – 30 razy (12 – 15 dB) słabsze, także czułość RT36 niewiele się poprawi. Dodatkowa powierzchnia to 1017.876 – 804.248 = 213.628 m², co stanowi 26.6 % obecnej apertury, ale (ze względu na wspomniane słabsze oświetlenie) zwiększy ona efektywną powierzchnię o mniej niż 2 % (26.6/15 = 1.8). Zatem, przy wykorzystaniu większości obecnie używanych oświetlaczy (wyjątkiem jest pasmo L) poprawa czułości RT36 w stosunku do RT32 wyniosłaby co najwyżej pojedyncze procenty.

Zwiększenie rozmiarów czaszy powinno
być związane z modyfikacja oświetlaczy.

Straty zysku anteny (gainu) RT36
przy użyciu obecnych oświetlaczy
i oświetlaczy zoptymalizowanych
do takich jak dla RT32
(obliczenia analityczne)

Taper Gain Diffr. First Feed Loss Subrefl. Sidelobe [dB] [%] [%] [%]
OCRA -15.154 19.5 1.23 0.47 -11.973 13.3 1.55 0.54 K/X -15.7 20.5 1.37/1.87 0.46 -12.0 13.4 1.79/2.44 0.54 C1/C2 -15.7 20.5 2.50/2.89 0.46 -12.0 13.4 3.27/3.78 0.54 L-OH -11.4 12.2 6.82 0.55 L-H -8.4 7.1 9.05 0.67 L-UHF -3.0 1.0 16.07 1.23

Zoptymalizowanie oświetlenia RT36 poprawi
jego skuteczną powierzchnię o 6 – 7 %.

Ostatnie zmiany: 28 stycznia 2009 r.

File partly translated from T_EX by T_TH, version 3.84.