Geometries assumed

The following table contains a few widely differing examples of assumed and computed geometrical and optical parameters obtained with the OptiCass program. The frequency dependent properties were calculated as if the paraboloid was not offset (no ray-tracing involved and closed formulae used instead) and using the parabolic on a pedestal illumination function with 12 dB taper at the dish edge.

Tab. 1: Examples of 80-meter offset telescope parameters

Parameter Set designation --> Set1 Set2 Set3 Set4 Set5 Circular aperture diameter, D 80.000 80.000 80.000 80.000 80.000 m Focal length, f 63.000 63.000 63.000 38.000 38.000 m Focal ratio, f/D_parent 0.350 0.350 0.332 0.200 0.200 Dish size ('vertical' diameter), D2 86.069 86.069 87.289 98.751 98.751 m Deepest dish point is off mid point by 16.282 16.282 18.197 24.925 24.925 m Dish depth, g_max 5.902 5.902 5.819 8.528 8.528 m Dish subtended angle - vertical plane 62.000 62.000 60.452 80.351 80.351 ° Dish subtended angle - laterally 60.610 60.610 58.903 71.544 71.544 ° Dish separation from optical axis, x1 10.000 10.000 15.000 15.000 15.000 m Optical axis to outermost dish point, x2 90.000 90.000 95.000 95.000 95.000 m Axis – subreflector furthermost edge point 10.000 10.000 15.000 15.000 15.000 m Height of secondary focus above parab. vertex, h 0.000 31.000 31.000 0.000 31.000 m Prime focus – subreflector furthermost point 10.571 10.571 15.602 15.375 15.375 m Prime focus to hyperboloid vertex, f1=c-a 6.583 6.150 8.047 4.682 2.068 m Secondary focus to hyperboloid vertex, f2=c+a 56.417 25.850 23.953 33.318 4.932 m Secondary interfocal length, f1+f2=2c 63.000 32.000 32.000 38.000 7.000 m Eccentricity of the hyperboloid, e=c/a 1.264 1.624 2.012 1.327 2.445 Ray path difference to the foci, (f-h)a/c 49.833 19.699 15.905 28.635 2.863 m Cassegrain telescope magnification, M=f2/f1 8.570 4.203 2.976 7.115 2.384 Effective focal length, F=M*f 539.894 264.790 187.513 270.386 90.609 m Aperture center angle as seen from sec. focus 5.302 10.787 16.687 11.615 33.766 ° Subreflector physical center angle 5.295 10.727 16.505 11.553 32.397 ° Subreflector subtended angle 8.468 17.126 23.849 16.750 45.866 ° Subreflector size in vertical plane 9.482 9.415 13.582 15.333 15.163 m Subreflector lateral size at center 8.623 8.338 11.389 11.189 7.478 m Subreflector depth at center 0.557 0.461 0.531 0.965 0.324 m Observing frequncy 4.997 GHz, wavelength 6.000 cm Half power beam width, HPBW ..................... 0.0500 0.0500 0.0500 0.0500 0.0500 ° First side lobe power level due to 12 dB taper .. 0.5351 0.5351 0.5351 0.5351 0.5351 % Gain loss due to diffraction at subreflector .... 2.4610 2.5027 2.1415 2.1605 2.6428 % Approximate Petzval radius of curvature ......... 15.7500 15.7500 23.6250 14.2500 14.2500 m Beam dev. due to primary translation ............ -0.8594 -0.8594 -0.8594 -1.3024 -1.3024·Xoff/m ° Beam dev. due to primary rotation ............... 1.9450 1.9450 1.9450 1.8638 1.8638·tilt/° ° Beam dev. due to secondary translation .......... -0.7534 -0.6437 -0.5559 -1.0912 -0.6875·Xoff/m ° Beam dev. due to secondary rotation about vertex 0.2032 0.1896 0.2476 0.2293 0.0999·tilt/° ° Beam dev. due to secondary rotation about focus . 0.1166 0.1204 0.1695 0.1401 0.0751·tilt/° ° Beam dev. due to feed translation in sec. focus . -0.1060 -0.2157 -0.3035 -0.2112 -0.6149·Xoff/m ° Feed offset per beamwidth, prime focus .......... -0.0582 -0.0582 -0.0582 -0.0384 -0.0384 m/HPBW Feed offset per beamwidth, secondary focus ...... -0.4719 -0.2320 -0.1648 -0.2369 -0.0814 m/HPBW

These data represent an 80 m × 86 to 99 m elliptical section of a paraboloid of revolution with focal length, f, of 38 or 63 m. A subreflector is mounted outside the telescope aperture (so that the latter is completely shadow-free). This secondary mirror is also a cut-out of hyperboloid of revolution but its edge is no longer a 2-D curve (although it fits circular cones that subtend it, whose vertices are at the foci). Its size is about 7–11 m × 9–15 m which corresponds to subtended angles (as seen from the secondary focus) ranging from 8° to 46°. The effective focal length of these Cassegrain systems ranges from 90 m to over 500 m.

Effect of offset dish on power pattern

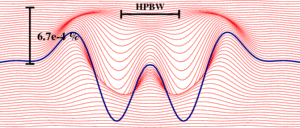
Fig. 1: Distortions of 80-meter telescope power pattern at 5 GHz with Set4 geometry due to asymmetry of the free-space taper alone. The distortions range here from –7 to +4 times 10–6 of the beam peak power. The blue curve is drawn along a section through this differantial pattern in the plane of symmetry (directed toward the u spatial frequency), that otherwise would be partly cancealed from view.

An assymetrical radio telescope construction in general will have the main beam somewhat distorted compared to a circularly symmetrical antenna. Fig. 1 presents the effect on power pattern resulting from an offset paraboloid with geometry of the Set4. Plotted there is the difference between the telescope actual power pattern and one with symmetrical free-space illumination function. The qualitative effect is similar for the other sets but the range varies and is greatest for the Set5, where the pattern differences reach –0.045% of the maximum. Thus these computations show that such kind of influence of assymetry is negligible in practice.

Focal field of view

An important property of a radio telescope is its sensitivity to feeds displacement from the focus. Cassegrain systems with axial symmetry are known for their good behaviour in this respect due to long effective focal lengths. The same can be expected of the offset paraboloid systems. Fig. 2 and Fig. 3 present detailed optical properties of a telescope corresponding to the Set1 geometry, the one with the longest effective focal length, and determined by the ray tracing method (as implemented in the OptiCass program). The computation of minimum losses for each lateral displacement consisted of optimizations of only two other parameters: the axial feed offset (in z-coordinate) and direction of peak radiation pattern at the feed. Thus the losses presented for all the displacements correspond to the same (nominal) position and tilt of the subreflector.

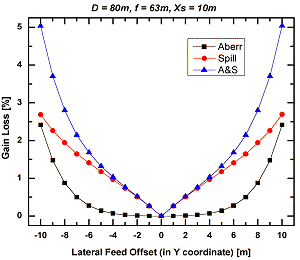
Fig. 2: Losses in antenna gain as a function of lateral displacement of feeds computed for the Set1 geometry and observing frequency of 5 GHz. The 'X-offset' (of the left panel) is in the plane of symmetry (determined by the optical axis and e.g. centre of the dish), and 'Y-coordinate' (of right panel) is perpendicular to this plane. The 'Aberr' losses (black symbols) represent fraction of peak power in the beam that gets lost when phase errors due to ray pathlengths are accounted for and the red dots mark similar measure of the power contained in properly weighted rays that fell outside the primary (dish) as a consequence of the squinted beam. These two effects combined are drawn in blue. Diffraction effects in these computations are neglected altogether.

As is seen in these diagrams, the Set1 geometry gives very wide field of view in the focal plane. It maintains small (below 1%) aberration losses as far as 10 m away from the focus towards the main mirror and 7 to 8 m backwards and sideways. This nice property worsens for other geometries (to practically break down for the Set5). This is illustrated in Tab. 2 where minimized losses are given for one arbitrarily chosen lateral feed offset of 5 m. They were obtained with the help of the o command of OptiCass which first minimizes the aberration loss with respect to the feed z-offset and then the 'total' (combined aberration, spillover and decentering of feed pattern) loss with respect to the feed radiation pattern deviation from its nominal direction in the respective zx- or zy-plane.

Tab. 2: Minimized losses at 5 GHz for 5-m lateral feed displacement from the secondary focus in the x- and y-coordinate. The Set5 is not included here because with this displacement it suffers too large distortions for meaningful estimates.

+5 m feed offset in x-coordinate Quantity and [units] Set1 Set2 Set3 Set4 Feed z-offset [m] 1.240 0.864 -0.100 0.705 Feed pattern x-offset [°] 0.373 1.599 2.119 0.735 Aberration loss [%] 0.024 1.503 15.974 6.037 Spillover loss [%] 1.040 2.272 2.586 1.206 Aberration & spillover [%] 1.064 3.740 18.147 7.170 Beam squint [°] -0.544 -1.130 -1.573 -1.114 same in beamwidths [HPBW] -10.9 -22.6 -31.5 -22.3 +5 m feed offset in y-coordinate Feed z-offset [m] 1.794 1.783 1.091 1.803 Feed pattern y-offset [°] 0.445 3.201 1.650 3.048 Aberration loss [%] 0.144 7.999 34.059 9.849 Spillover loss [%] 1.175 2.550 4.479 0.877 Aberration & spillover [%] 1.317 10.345 37.012 10.640 Beam squint [°] -0.543 -1.116 -1.518 -1.087 same in beamwidths [HPBW] -10.8 -22.4 -30.4 -21.7

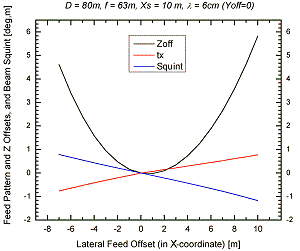
Fig. 3: Offsets in z-coordinate (black curves) and direction of feed radiation pattern (angles tx and ty) required to minimize aberration losses for feed lateral offsets in x- (left panel) and y-coordinate (right panel). Noteworthy, the radius of curvature of the optimal surface near the focus (about 1 to 1.5 m) is in marked contrast with the Petzval radius as given in Tab. 1 (15 m). Plotted in this diagram is also the beam deviation with respect to the optical axis (axis of the parent paraboloid) of a telescope with geometry of the Set1 (the blue line in the left panel and similar but green line in the right panel).

One may note on passing that for x-offset of +10 m the beam deviation in the zy-plane (–1.044°) of Fig. 3 agrees quite well with the value of Tab. 1 (–1.060°) calculated for normal telescope while that in zx-plane (–1.118°) deviates from it only slightly further away (and in opposite direction). This agreement degrades somewhat for geometries with shorter effective focal lengths, but even for the Set5 the classical formulation overestimates this parameter by only about 22%.

Sky field of view due to subreflector tilts

Nutations of the subreflector are frequently used to rapidly chop the beam on the sky for reference purposes. In transit telescopes such a movement may be used for source tracking. Tab. 3 presents gain losses and beam throws associated with the secondary mirror tilt by 5° for the five geometries. These results were obtained by minimizing of the combined aberration and spillover quantity as a function of the secondary position (which reduces to searching for an optimal centre for the rotation). It can be concluded that if a few percent of the aberration losses are to be the limiting factor, the field of view essentially does not exceed ±1° in any of the analysed cases, and only being very tolerant one could count at best on ±2° using the Set4.

Tab. 3: Minimized losses at 5 GHz for +5° rotation of the secondary
about the prime focus in the yz plane

Quantity [units] Set1 Set2 Set3 Set4 Set5 Subreflector y-offset [m] 0.035 0.070 0.186 0.040 0.124 Subreflector z-offset [m] -0.054 -0.049 -0.062 -0.084 -0.026 Aberration loss [%] 1.905 2.573 5.413 1.309 2.460 Spillover loss [%] 7.177 7.821 8.033 3.461 3.557 Aberration & spillover [%] 8.945 10.193 13.012 4.724 5.930 Beam squint [°] 0.561 0.561 0.751 0.668 0.301 same in beamwidths [HPBW] 11.2 11.2 15.0 13.4 6.0

Starting parameter set

Circular aperture diameter, D 90.000 m Focal length of primary mirror, f 30.000 m Subreflector diameter, d 8.000 m Height of secondary focus above paraboloid vertex, h 5.000 m Cassegrain telescope magnification, M=f2/f1 9.000 Effective focal length, F=M*f 270.000 m Subreflector subtended angle 19.055 deg Primary dish --> Symmetrical ------Offset paraboloid----- D=90m, d=8m D=90x125m, d=9x15m Feed lateral offset [m] 1 5 +1V -1V 1H 5H(V) 5H(H) Beem offset [deg] 0.21 1.03 0.21 0.20 0.207 -0.17 -1.01 Gain loss [%] 5.09 99.19 3.86 14.42 5.53 97.71 Optimal z [m] 0.189 0.96 -0.07 0.37 0.142 2.535 Beem offset [deg] 0.21 0.53 0.21 0.21 0.208 -0.09 -1.12 Minimized gain loss [%] 0.93 98.69 3.25 2.95 3.209 88.74

NOTES:
1) The high losses are mainly due to aberration.
2) For offset paraboloid the direction of feed displacement is defined positive toward the outermost point of main dish in 'vertical' (V) plane; horizontal displacements (H) cause both 'vertical' H(V) and horizontal H(H) beam offsets.
3) The assumed wavelength is 2 cm (about 15 GHz).

Results in the next three tables (with one exception in the last table) are obtained without optimization of z-coordinate of feed and the feed direction is uniformly set towards centre of the subreflector. 'Feed o. angle' stands for the subreflector subtended angle (i.e. as seen by the feed).

Constants: freq=15 GHz, D=90 m, d=8 m, h=5 m, feed_offset=2 m Focal length, f [m]: 25 30 35 40 45 50 Beam offset [deg] 0.52 0.42 0.36 0.31 0.27 0.24 Losses [%] 88.9 56.6 26.9 13.1 7.02 4.24 Feed o. angle [deg] 23.09 14.0 11.0 Constants: freq=15 GHz, D=90 m, d=8 m, f=40 m, feed_offset=2 m Feed height, h [m]: 0 5 10 15 20 25 Beam offset [deg] 0.27 0.31 0.37 0.44 0.57 0.78 Losses [%] 7.86 13.1 23.5 45.7 81.6 93.6 Feed o. angle [deg] 12.2 14.0 16.5 20.1 25.7 35.3 Constants: freq=15 GHz, D=90 m, d=8 m, f=50 m, feed_offset=2 m Feed height, h [m]: 0 5 10 15 20 25 25opt Beam offset [deg] 0.22 0.24 0.28 0.32 0.38 0.47 0.48 Losses [%] 3.02 4.2 6.5 10.7 19.7 39.6 5.4* Feed o. angle [deg] 9.8 11.0 12.5 14.5 17.2 21.1 21.1   * minimized aberration losses.

The following results are optimized for minimum aberration losses only (except for the last two columns of the table).

Constants: freq=15 GHz, D=90 m, d=8 m, f=50 m, h=25 m Feed offset [m] 1 2 3 4 4* 4** Optimum z of feed [m] 0.12 0.49 1.10 1.93 1.74 1.93 Beam offset [deg] 0.24 0.48 0.73 1.01 0.90 1.01 Minimized losses [%] 1.48 5.4 16.5 37.9 15.8 7.6  * Abberation and alignment (spillover) losses minimized by varying z and subrelfector horizontal tilt (optimum is at 0.94 deg) ** These data are computed for 5 GHz and the same configuration as for 15GHz, 4 m feed offset.

CONCLUSION: At wavelength of 2 cm (15 GHz) and with shorter focal lengths, f, say less than about 40 m, it will be difficult to obtain required field of view corresponding to ±5 minutes of observing time at transit, or ±1.25°, without excessive losses. For f = 50 m this criterion could be reached with feed offsets somewhat larger than ±4 m and simultaneous corrections to subreflector direction of the order of 1°.

Would the following solution do?

The table summarizes RT90 configuration for minimized losses with 6 m feed offset, that fulfills the requirement of 10 minutes observations at transit. Here the main beam is 1.3° offset and losses exceed 20 % in power while the sidelobe level gets as high as 18 % of the main beam.

Circular aperture diameter, D 90.000 m Dish size ('vertical' diameter), D2 90.000 m Focal length of primary mirror, f 50.000 m Focal ratio of primary mirror, f/D 0.556 Telescope F-number (or F/#): F_eff/D 2.705 Dish depth, g_max 10.125 m Dish subtended angle 96.911 deg Dish separation from axis, x1 -45.000 m Axis to outermost dish point, x2 45.000 m Height of secondary focus above paraboloid vertex, h 25.000 m Axis – subreflector outer edge distance 4.000 m Prime focus – subreflector outer edge distance 5.344 m Prime focus to hyperboloid vertex, f1=c-a 4.260 m Secondary focus to hyperboloid vertex, f2=c+a 20.740 m Secondary interfocal length, f1+f2=2c 25.000 m Eccentricity of the hyperboloid, e=c/a 1.517 Ray path difference to the foci, (f-h)a/c 16.481 m Cassegrain telescope magnification, M=f2/f1 4.869 Effective focal length, F=M*f 243.454 m Dish edge +angle as seen from secondary focus -71.708 deg Dish edge -angle as seen from secondary focus 71.708 deg Subreflector subtended angle 21.121 deg Subreflector diameter 8.000 m Subreflector depth at center 0.715 m Extension of subreflector blind spot 0.682 m Subreflector pivot coordinates, x,y,z 0.000 0.000 0.000 m Subreflector tilt towards +ve X and Y 0.000 2.785 deg Feed offsets in x, y and z 0.000 6.000 3.771 m Feed pattern nominal angles wrt YZ,XZ planes 0.000 -18.844 deg and respective offsets 0.000 1.746 deg Observing frequency [GHz] and wavelength 14.990 2.000 cm Assumed z-coordinate for aperture plane -44.938 m Number of rays traced 2912 Number of pattern bins in u.v dimensions 41.041 Span of u coordinate [spacial cycles] 5.000 Span of v coordinate 5.000 Beam offset, vertically (downward +ve) 0.000 deg Beam offset, laterally (leftward +ve) -1.327 deg HPBW, beamwidth in vertical plane 0.874 ' same in orthogonal plane (laterally) 1.016 ' Free space illumination taper or just asymmetry 0.073 dB Feed illumination taper at the edge 12.000 dB Ray tracing aberration loss 23.569 % Ray tracing spillover loss 4.143 % Loss due to decentered illumination -4.066 % Pattern distortions range (min and max): -2.991 17.981 % Analytic computations valid for symmetric reflector antenna (classical optics approximation for parabolic on pedestal illumination) Half power beam width (Baars 2003) .............. 0.0148 [deg] First side lobe power level due to taper (Baars) 0.5351 [%] Gain loss due to tapered illumination ........... 10.6659 [%] Gain loss due to diffraction at subrefl. (Lamb) . 1.4752 [%] Astigmatic gain loss due to lateral feed offset . 378.9590 [%] Coma gain loss due to lateral feed offset ....... 7.8835 [%] Aberration (astigmatism & coma) gain loss ....... 386.8425 [%] Petzval surface radius (inverse field curvature) 3.9252 [m] Beam dev. due to primary translation (Baars) .... -1.0268*Xoff/m [deg] Beam dev. due to primary rotation ............... 1.8961*tilt/deg [deg] Beam dev. due to secondary translation .......... -0.7927*Xoff/m [deg] Beam dev. due to secondary rotation about vertex 0.1611*tilt/deg [deg] Beam dev. due to secondary rotation about focus . 0.1022*tilt/deg [deg] Beam dev. due to secondary rotation about "z_piv" 0.1022*tilt/deg [deg] Beam dev. due to feed translation in sec. focus . -0.2342*Xoff/m [deg] Feed offset per beam width, prime focus (Baars) . -0.0144*NoOfBeams [m] Feed offset per beam width, secondary focus ..... -0.0633*NoOfBeams [m]

OptiCass output for the design SETTABLE parameters # #0 #1 #2 #3 #4 Cassegr.: D,X_min,f,Xs_max/-f2,h2 [m] 0 90.000 -45.000 50.000 4.000 25.000 Subreflector: x,y,z, tx, ty [m,deg] 1 0.000 0.000 0.000 0.000 2.785 Feed offsets: x,y,z, Dtx,Dty [m,deg] 2 0.000 6.000 3.771 0.000 1.746 Ray-tracing: N/R.NxNy,Nu,Nv,maxU,maxV 3 30.0000 40. 40. 2.500 2.500 Wavel,Taper,zAprt,pltD,pivot [m,dB,-] 4 0.020 12.000 -44.938 2. 0. Press ?,ENTER,g,$,c,m,o,a,p #i, or #i value (e.g. 21 6.000): COMPUTED param's & x,z_piv,du,v,N 0.000 0.000 0.000 0.046 205.000 Main dish: f/D,f/Dp, D2, G,coordG [m] 6 0.5556 0.5556 90.000 10.125 45.000 angles: t_V,t_H, t_0, t_1, t_2 [deg] 7 96.911 96.911 0.000 -48.455 48.455 Subreflector: Dc,Dm,Ds2,Gs,Xs_min [m] 8 8.0000 8.0000 8.0000 0.7152 -4.0000 feed angles: t_VH,t_c,_0,_1,_2 [deg] 9 21.1210 0.0000 0.0000-10.5605 10.5605 Cassegrain: f1, f2, fs, F, M [m,-] 10 4.2596 20.7404 25.0000 243.454 4.8691 Hyperbola: a,c,b,e, FSAmpRatio [m,-] 11 8.2404 12.5000 9.3992 1.5169 0.9916 Beam: t_u,t_v, HPBW_u,_v,_0 [deg] 12 0.0000 -1.3273 0.0146 0.0169 0.0148 Squint, phi_X,Y, apert_X,Y [deg,m] 13 1.3273 0.0000-18.8439 0.0000-10.4558 Loss: Aberr,Spill,A&S,IllDec,Totl [%] 14 23.5693 4.1429 26.7357 -4.0657 23.7570 pathR,ComaLow,-Hi,1stLob,Totl'[m,%] 15 2.1046 -2.9913 17.9812 1.3284 25.394

[May 14, 2009]