Fizyka w Szkole, XXXVIII (1992),
z. 5, 292–299.
dr Kazimierz M. Borkowski
Toruń — Katedra Radioastronomii UMK
Czy potrzebna jest reforma kalendarza gregoriańskiego?
Wstęp
Istnieją trzy duże grupy kalendarzy:
słoneczne, księżycowe i
księżycowo-słoneczne. Podstawą pierwszych jest astronomiczny
okres obiegu Ziemi wokół Słońca, tzw. rok zwrotnikowy, albo
czas upływający między kolejnymi równonocami (wiosennymi bądź
jesiennymi) lub przesileniami (letnimi bądź zimowymi). Kalendarze
księżycowe liczą miesiące synodyczne, tj. okresy powtarzania
się takich samych faz Księżyca — z reguły od jednego nowiu do
następnego. Ponieważ średnia długość miesiąca synodycznego
wynosi 29,53 dni (rzeczywista wartość zmienia się w granicach od
29,268 do 29,838 dni [1]), to kalendarze te mają na ogół na
przemian 29- i 30-dniowe miesiące. Najbardziej rozpowszechnionym
kalendarzem księżycowym jest kalendarz muzułmański
(mahometański). Lata liczone są tam w cyklach po 30, z których
19 ma po 354 (6·29 + 6·30) dni,
a 11 (przestępne) — po 355 dni. Dzień nowego roku cofa się więc
dość szybko po datach naszego kalendarza przez wszystkie pory roku.
Aby wyhamować takie cofanie się dat kalendarzowych względem pór
roku w kalendarzach księżycowo-słonecznych co kilka lat wprowadza się
dodatkowy miesiąc przestępny. Najważniejszym z nich jest kalendarz
żydowski (hebrajski) oparty o tzw. cykl Metona. W
19 latach tego cyklu lata o numerach 3, 6, 8, 11, 14, 17 i 19 są
przestępnymi (13-miesięcznymi). Taka konstrukcja zapewnia, że
nowy rok tego kalendarza oscyluje między 5 września i 5 października
w naszym kalendarzu.
Obowiązujący u nas (i powszechnie) od ponad 400 lat kalendarz
gregoriański jest kalendarzem słonecznym. Oznacza to, że jego reguły
dobrano tak, by pory roku nie przesuwały się względem dat kalendarzowych.
Reguły te stanowią, że normalnie lata liczą po 365 dni, ale lata
podzielne przez cztery, wyjąwszy lata ``setkowe'' niepodzielne przez
400, są przestępnymi — tj. o 366 dniach. Pory roku określa położenie
Słońca względem równika niebieskiego (który jest przekrojem sfery
niebieskiej płaszczyzną równika ziemskiego). Astronomowie przyjmują,
że np. wiosna rozpoczyna
się w chwili przechodzenia Słońca z południowej półkuli nieba na
północną. To miejsce na równiku jest nazywane punktem równonocy
wiosennej bądź punktem Barana (kiedyś punkt ten leżał w
gwiazdozbiorze o takiej nazwie). Dwa kolejne przejścia Słońca przez
punkt Barana wyznaczają wspomniany już rok zwrotnikowy.
Idealny kalendarz słoneczny powinien liczyć lata synchronicznie z obiegami
Słońca po ekliptyce (widomej drodze Słońca na sferze niebieskiej,
w odniesieniu do gwiazd), lecz te ostatnie nie wyrażają się całkowitą
ilością dni; gorzej — rok zwrotnikowy nie ma stałej długości.
Stąd rodzą się trudności w praktycznej realizacji kalendarzy
słonecznych. W poprzednim kalendarzu — juliańskim — co czwarty rok
był przestępnym, tzn. średnio w roku było 365,25 dni. Ponieważ
średni rok zwrotnikowy ma około 365,2422 dni, oznaczało to powolne
ale systematyczne (z szybkością 365,25 – 365,2422 = 0,0078 doby na
rok, albo mniej więcej trzech dób na 400 lat) cofanie się
pór roku po datach tego kalendarza. Skutkiem tego w okresie od roku 45
p.n.e., kiedy to Juliusz Cezar wprowadził ten kalendarz, do reformy
gregoriańskiej w 1582 r. data równonocy wiosennej (początku wiosny)
cofnęła się z 21 marca na 10 marca.
Kilkunastodniowe przesunięcie pór roku w kalendarzu nie jest jeszcze
powodem do alarmu, zwłaszcza gdy ,,utrata'' kolejnego dnia nastąpi
dopiero za ponad 100 lat. W rzeczy samej, reforma którą przeprowadzono
miała podłoże religijne, a konkretniej chodziło o problem daty
Wielkanocy. Zgodnie z Nowym Testamentem ukrzyżowanie Jezusa z
Nazaretu miało miejsce w piątek 14 albo 15 dnia żydowskiego miesiąca
Nisan, a więc 14 – 15 dni po wiosennym nowiu Księżyca — w czasie,
gdy naród Izraela rozpoczynał uroczyste świętowanie kolejnej rocznicy
ucieczki z Egiptu (Paschy).
Stąd ustaliła się tradycja obchodzenia Wielkanocy w najbliższą
niedzielę po pierwszej wiosennej (przypadającej po 21 marca) pełni
Księżyca. Nowy kalendarz opracowała specjalna komisja, która
oparła się na propozycji lekarza i wykładowcy uniwersytetu Perugii,
A. Liliusa (podobno w tej sprawie konsultowano się także M. Kopernika).
Ostatecznie, bulla papieża Grzegorza XIII nakazywała, by
po czwartku 4 października 1582 r. następowała data piątek 15
października 1582 r. i by niektóre z lat ,,setkowych'' dotąd
przestępnych stały się w przyszłości latami zwykłymi.
Z nowych reguł wynika, że w każdych kolejnych 400 latach jest 97
lat przestępnych, co także znaczy, że średni rok kalendarzowy
ma 365[ 97/400] = 365,2425 dni. Różnica względem astronomicznego
okresu powtarzania się pór roku wynosi zatem teraz tylko 0,0003 dnia, a to
implikuje cofanięcie się początku wiosny o 1 dzień dopiero za około
3000 lat. Rozumowanie takie powoduje, że dominuje zgodność opinii,
iż nasz obecny kalendarz, chociaż i on nie jest doskonały,
nie wymaga żadnej korekty w częstotliwości i sposobach wprowadzania
lat przestępnych jeszcze przez tysiące nadchodzących lat.
Nie oznacza to bynajmniej całkowitej zgodności opinii. Co kilka lat bowiem
pojawiają się publikacje sugerujące, że wcześniej czy
później reforma kalendarza gregoriańskiego będzie konieczna (np. [2]
i [3]). W pracach takich na ogół używa się rozumowania, któreśmy
tu podali, a które polega na porównaniu sumy długości
lat zwrotnikowych (po 365,2422 dni albo z niewielkim składnikiem zależnym
od czasu i wyrażającym zmienność długości tego okresu) z
odpowiednią sumą dni kalendarzowych. Na przestrzeni jednego lub dwóch
tysięcy lat sposób ten daje poprawne wyniki, lecz w swej istocie
jest niepoprawny, co uzasadnię później w tym artykule. Kiedy w grę
wchodzą dziesiątki tysięcy lat, to pojawia się następny kłopot,
gdyż autorzy takich analiz zapominają, że współczesne wzory
analityczne opisujące średni ruch Słońca po niebie, tzw. długość
ekliptyczną, a z których można obliczyć długość roku
zwrotnikowego, są ważne na przestrzeni zaledwie kilku tysięcy lat.
Wreszcie, autorzy ci zwykle pomijają w swoich rachunkach zmienną
długość doby kalendarzowej, a ta przecież systematycznie wydłuża
się na skutek wyhamowywania rotacji Ziemi przez oddziaływania pływowe
(głównie Księżyca). Zmienność doby powoduje, że nawet lata o
takiej samej liczbie dni mają różną długość, a to trzeba
uwzględnić w ścisłych rachunkach kalendarzowych.
Bliższa analiza pokazuje, że nasza współczesna wiedza dotycząca
ruchu Ziemi pozwala planować kalendarze nie dalej niż na jakieś 2, może
(optymistycznie) 3, tysiące lat na przód i że pójście znacząco
dalej oznacza czystą spekulację o znikomym lub żadnym znaczeniu dla
praktyki. W całym tym okresie kalendarz gregoriański bardzo dobrze oddaje
lata zwrotnikowe nie pozostawiając żadnych solidniejszych podstaw do
ewentualnej reformy. Pokażemy to na dalszych stronach.
Długość ekliptyczna Słońca a kalendarz
Naturalną podstawą zliczania mijających lat
zwrotnikowych jest długość ekliptyczna Słońca mierzona od precesującego
punktu równonocy wiosennej (Barana). Gdy długość ta osiąga
wielokrotność 360°, wtedy Słońce przechodzi przez
ten punkt i można przyjąć, że rozpoczyna się nowy rok słoneczny.
Według współczesnej teorii ruchu orbitalnego Ziemi, VSOP82 [4],
średnia (tzn. pomijając perturbacje okresowe) długość Słońca
wynosi
|
L = 280°27'59,2146'' + 129602771,36329''T +
1,093241''T2 + 0,0000762''T3, |
| (1) |
gdzie T jest równomiernym czasem mierzonym wiekami juliańskimi od
fundamentalnej epoki J2000 (południe czasu dynamicznego 1 stycznia 2000 r.),
tj.
JED w tym określeniu jest datą juliańską — kolejnym numerem
dnia licząc od południa 1 stycznia 4713 r.p.n.e. (wg. kalendarza
juliańskiego). Zakłada się tutaj, że wszystkie dni (doby) są
równej długości, po 86 400 sekund atomowych (układu SI). Dla
odróżnienia od dni juliańskich JD, liczonych jednostkami
niejednostajnego (bo zależnego od rotacji Ziemi) czasu uniwersalnego,
JED często nazywa się efemerydalnymi dniami juliańskimi.
Podstawowe znaczenie ma wiarogodność wyrażenia (1) i zakres jego
stosowalności. Okazuje się, że dokładność tego wzoru jest
całkowicie zadowalająca w przypadku dyskusji kalendarzy, gdyż na
większych przedziałach czasowych, kiedy nie można już mu ufać,
precyzję ogranicza nieokreśloność dobowej rotacji Ziemi. Sprawdziłem
to [5] przez porównanie z pełniejszą reprezentacją przedstawioną
przez Laskara [6]. Według tego autora błąd długości Słońca
obliczonej zgodnie z jego algorytmem sięga kilku sekund łuku dla
T = ±100, tj. 10 000 lat od współczesności.
W tak odległej epoce wyniki Laskara różnią się od wartości VSOP82
o około 0,6°, zatem możemy przyjąć, że
taki jest maksymalny błąd
naszego prostego wzoru (oczywiście, błąd ten szybko maleje dla epok
zmierzających do J2000). Dodajmy, że do tego miejsca w czasie, różnice
między teorią VSOP82 i do niedawna powszechnie obowiązującą
sędziwą już teorią Newcomba są w tym kontekscie zaniedbywalne.
Zauważamy też, że błąd 0,6° w długości
ekliptycznej Słońca transformuje się na bląd około 0,6 dnia w
kalendarzu słonecznym, co w skali 10 000 lat nie jest jeszcze groźne.
Sytuacja jednak gwałtownie pogarsza się gdybyśmy zapragnęli
pójść znacząco dalej w czasie, gdzie ponadto nie mamy informacji
o dokładności wzorów Laskara (bo zostały opracowane dla konkretnego
przedziału czasu). Dysponując zatem opublikowanymi wyrażeniami na
średnią długość ekliptyczną Słońca, analizy kalendarzy
musimy ograniczać w czasie do 10 000 lat lub tylko nieznacznie dalej.
Opuszczając nieistotny dla tych rozważań składnik stały z
prawej strony równania (1) i
dzieląc pozostałe współczynniki liczbowe przez 1 296 000'', tj.
przez ilość sekund łuku w pełnym obrocie o 360°, dostajemy
bardzo wygodne wyrażenie na obliczanie ilości obiegów Słońca
wokół ekliptyki, czyli ilości lat zwrotnikowych, które upłynęły
od epoki J2000 do chwili T:
|
Lτ = 100,0021383976·T + 8,43550·10–7·T2 + 5,88·10
–11·T3. |
| (3) |
To tę liczbę należy porównać z ilością lat kalendarzowych
zliczonych w tym samym czasie. W kalendarzu juliańskim jest po prostu
100·T lat kalendarzowych w T wiekach. Dla kalendarza
gregoriańskiego, w którym — jak mówiliśmy — lata mają średnio
po 365,2425 dni, mamy
lat kalendarzowych w T wiekach juliańskich.
Różnicę w zliczaniu lat zwrotnikowych (równanie (3)) i
kalendarzowych (4) można wyrazić w dniach przez pomnożenie jej
przez 365,2425. Dostajemy wtedy praktycznie użyteczną formułę:
|
N' = 0,03103369·T + 3,08100·10–4·T2 + 2,147·10–8·T3. |
| (5) |
Użyliśmy tutaj współczynnika 365,2425, który jest w zasadzie
właściwy tylko dla kalendarza gregoriańskiego. Jego wartość nie
jest jednak krytyczna: nawet trzycyfrowe zaokrąglenie, tj. liczba 365,
wydaje się zadowalające o ile końcowa różnica N' dla innego
kalendarza słonecznego (tj., także innego wzoru (4))
nie jest zbyt duża — powiedzmy, gdy jest mniejsza od pełnego roku
(nawet w tym skrajnym przypadku dostalibyśmy wynik z błędem nie
przekraczającym jeszcze 0,25 dnia).
Otrzymany w ten sposób wzór mówi nam o ile dni kalendarz gregoriański
wyprzedza astronomicznie ścisły kalendarz przy założeniu,
że oba były zgodne w chwili J2000. Na przykład, biorąc T = 20 (epoka
J4000) dostaje się N' = 0,74d. Oznacza to, że po 2000 lat od dziś
data równonocy wiosennej (mówmy 20 marca) przesunie się o prawie dzień
wstecz w kalendarzu gregoriańskim (mówmy na dzień 19 marca około
4000 r.). Tak więc na upartego po tylu latach, a raczej nieco wcześniej
— kiedy N' ≈ 0,5d, należałoby
poprawić kalendarz gregoriański poprzez uczynienie jednego z lat
przestępnych rokiem zwykłym (o 365 dniach).
Wpływ rotacji Ziemi na kalendarz
W dotychczasowych rozważaniach zakładaliśmy,
że dni kalendarzowe
mają stałą długość równą 86 400 atomowych sekund. Wiemy jednak,
że Ziemia rotuje nader nierównomiernie i długość doby powoli
rośnie. Prawdziwa ilość dni kalendarzowych (ilość obrotów Ziemi
względem Słońca), jakie upłynęły między J2000 i dowolną inną
epoką określoną przez T, formalnie wynosi
|
n = | ∫
|
T
0
|
Ω dT = 36525·T – |
ΔT – DTo
86400
|
, |
| (6) |
gdzie Ω = Ωo– ω jest rzeczywistą kątową
prędkością obrotu Ziemi, na którą składa się ściśle jeden
obrót w ciągu 86 400 sekund SI (Ωo) oraz przyczynek zmienny
(ω = [(dΔT)/dT]),
ΔT reprezentuje zakumulowaną różnicę między
ziemskim czasem dynamicznym (albo czasem efemeryd) a czasem uniwersalnym
wyrażoną, jak się to zwykle czyni, w sekundach, zaś
ΔTo jest
tą różnicą dla T = 0. Ze względu na małość tej ostatniej wielkości
(ΔTo
≈ 65 s), dla uproszczenia notacji, w
dalszej dyskusji pominiemy ją całkowicie bez obawy o utratę dokładności.
Uwzględnienie zmiennej rotacji
Ziemi w naszych rozważaniach będzie polegało na zastąpieniu
poprzedniego wyrażenia na LK, wzoru (4),
przez LK = n/365,2425.
Jest to równoważne zwiększeniu N' o ΔT
przeskalowane z sekund na doby:
|
N = ((2,147·10–8T + 3,081·10–4)T + 0,03103369)T + |
ΔT
86400
| . |
| (7) |
Rzeczywistym problemem jest to, że obecnie nie potrafimy dokładnie
przewidzieć długości doby nawet na niedaleką przyszłość, nie
mówiąc już o tysiącach czy milionach lat. Liczne współczesne oceny
przebiegu ΔT (który normalnie modeluje się parabolą) na dużych
przedziałach czasu wykazują wzajemne rozbieżności znacznie większe od
błędów formalnych. Jedna z ostatnich
kompilacji wyznaczeń tego parametru opartych o obserwacje teleskopowe
[7] prowadzi do następującego wyniku (w sekundach)
|
ΔTMB = 48,75 + 48,1699·T + 13,3066·T2. |
| (8) |
Wzór ten przewiduje raczej małe wartości dla
ΔT. Z drugiej
strony, również niedawne studium obserwacji
historycznych obejmujących lata od 390 p.n.e. do 948 n.e. [8],
dało całkiem inny obraz rotacji Ziemi:
|
ΔTSM = 2177 + 408,6·T + 44,3·T2. |
| (9) |
W literaturze można znaleźć wiele innych wyznaczeń
ΔT, jednak
te dwa wydają się ograniczać znakomitą większość z pozostałych.
I chociaż możnaby wskazać więcej argumentów na korzyść wyniku
Stephensona i Morrisona w przypadku odległych epok, to tutaj potraktujemy
oba rezultaty równoprawnie jako wyznaczające przedział przyszłych
dopuszczalnych wahań rotacji Ziemi. W takim razie, w roku 4000 (T =
20, ΔT od 6300 do 28 000 sekund) ze wzoru (7) będziemy mieli 0,8d < N <
1,1d zamiast 0,74d. Ten rezultat upoważnia nas do
stwierdzenia z przekonaniem, że nasz kalendarz gregoriański nie
wyprzedzi astronomicznego o znacząco więcej niż 1 dzień jeszcze przez
najbliższe 2000 lat.
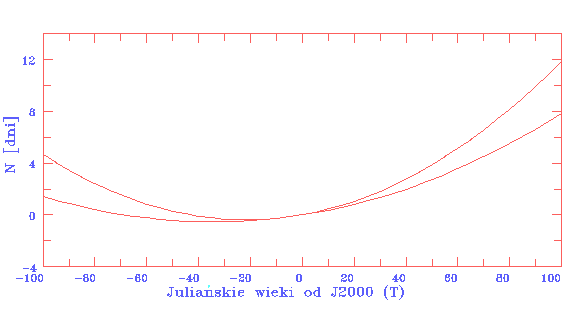 |
Rys. 1. Różnica w liczbie lat zwrotnikowych i
gregoriańskich obliczona zgodnie z równaniem (7).
Dwie krzywe odpowiadają różnym modelom zakumulowanego zwalniania dobowej
rotacji Ziemi: równanie (8) (dolna krzywa) i (9) (krzywa górna). |
Podobny rachunek dla 10 000 lat od teraz (T = 100; Rys. 1) jest
o wiele bardziej rozczarowujący: 8d < N < 12d.
Taka niepewność wespół
z całkiem zadowalającym zachowaniem się naszego kalendarza w
najbliższych tysiącleciach czynią próby reform tego kalendarza
z jednej strony przedwczesnymi, a z drugiej zbytecznymi. Można spekulować,
że jeśli nawet nasza cywilizacja przetrwa wszystkie prawdopodobne rewolucje
(społeczne, naukowe i techniczne) przyszłości, to okaże się, że
wcale nie zależy jej na precyzyjnej synchronizacji kalendarza z datami
świąt kościelnych (przypomnijmy, że reforma gregoriańska miała
na celu przede wszystkim pogodzenie daty Wielkanocy z datą równonocy
wiosennej). Dla kogoś, kto upierałby się jednak przy potrzebie reformy
może lepszym wyda się kontrargument, że przyszłe
pokolenia będą kontrolować rotację Ziemi (a może i jej obieg
wokół Słońca) w taki sposób, aby nie trzeba było korygować
reguł kalendarza!
Rok zwrotnikowy i inne okresy orbitalne
Rok zwrotnikowy jest typowym okresem orbitalnym jakich wiele spotyka
się w astronomii w związku obrotami ciał niebieskich. Z mechaniki nieba,
z praw Keplera wiemy, że każdy okres jest w zasadzie odwrotnością
średniego ruchu — średniej orbitalnej prędkości kątowej.
W rzeczywistości nigdy nie mamy do czynienia z czysto keplerowskimi orbitami,
gdyż nie istnieją izolowane układy podwójne. W praktyce jednak
przybliżenie takie jest często zadowalające, a na ogół przynajmniej
może służyć jako pierwsze przybliżenie, do którego dodaje się
funkcje perturbacyjne. Zmienne elementy orbit, które
występują w analitycznych teoriach ruchu planet, podaje się w funkcji
czasu (efemeryd bądź dynamicznego) w postaci szeregów potęgowych
niskiego (2, 3 lub wyższego) stopnia na ogół w układzie ekliptycznym.
Rodzi się pytanie, jak w tej sytuacji obliczać długość zmiennych
okresów obiegu. I chociaż sprawa jest raczej elementarna, trudno byłoby
polecić Czytelnikowi jakąś pozycję literatury. Z drugiej strony,
wszystkie najważniejsze roczniki astronomicznie podają
regularnie aktualne wartości liczbowe długości różnych lat i
miesięcy. Choćby z tego powodu warto omówić to zagadnienie szerzej.
Moglibyśmy poprzestać na określeniu długości roku zwrotnikowego,
jednakże sytuacja z innymi okresami jest bardzo podobna — autorzy
podstawowych opracowań zdają się traktować je jako nazbyt oczywiste
by poświęcić im nawet kilka zdań, nie mówiąc już o podaniu
jakichkolwiek wzorów praktycznych. Poniższe definicje i pełny przykład
dla roku zwrotnikowego powinny zaspokoić gros potrzeb w tym zakresie.
Bodaj najważniejszym ze wspomnianych keplerowskich elementów orbitalnych
jest średnia długość ekliptyczna ciała na orbicie, gdyż
zawiera zarówno informacje o okresach obiegu, jak też o chwili przejścia
przez punkt Barana. Taką wiekość już używaliśmy w postaci wzoru
(1). W ogólności ma ona postać:
L = M + 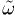 |
= Lo + aT + bT2 + cT3 + ... |
| (10) |
gdzie M jest anomalią średnią, 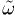 —
ekliptyczną
długością wstępującego węzła orbity zwiększoną o kątową
odległość peryhelium od węzła, T — czasem liczonym zwykle w
stuleciach juliańskich od epoki standardowej, a współczynniki
a, b, c i ewentualnie dalsze podaje się w stopniach lub sekundach łuku.
Z długości ekliptycznych (10) można łatwo obliczyć kilka
różnych okresów (w przypadku orbity Ziemi mówimy o latach, a o
miesiącach dla Księżyca).
—
ekliptyczną
długością wstępującego węzła orbity zwiększoną o kątową
odległość peryhelium od węzła, T — czasem liczonym zwykle w
stuleciach juliańskich od epoki standardowej, a współczynniki
a, b, c i ewentualnie dalsze podaje się w stopniach lub sekundach łuku.
Z długości ekliptycznych (10) można łatwo obliczyć kilka
różnych okresów (w przypadku orbity Ziemi mówimy o latach, a o
miesiącach dla Księżyca).
Okres (rok, miesiąc) zwrotnikowy dotyczy odstępu czasu pomiędzy
dwoma kolejnymi przejściami ciała przez punkt równonocy wiosennej:
|
τ = |
360°
|
= |
360°
a + 2bT + 3cT2 + ...
|
≈ |
360°
a
|
| (
|
1 – 2 |
b
a
|
T – 3 |
c
a
|
T2 – ... | ) |
, |
| (11) |
gdzie  oznacza pochodną po czasie (T) z L, zaś 360°
umieściliśmy w liczniku przy założeniu, że a, b, c, ...
wyrażono w stopniach; jeśli współczynniki te dane są w sekundach
łuku, wtedy w liczniku piszemy 360·3600'' — tak, jak w przykładzie
przy końcu tego punktu.
oznacza pochodną po czasie (T) z L, zaś 360°
umieściliśmy w liczniku przy założeniu, że a, b, c, ...
wyrażono w stopniach; jeśli współczynniki te dane są w sekundach
łuku, wtedy w liczniku piszemy 360·3600'' — tak, jak w przykładzie
przy końcu tego punktu.
Okresem synodycznym (od złączenia w długości do następnego
złączenia) dwóch obiektów o średnich długościach ekliptycznych
L1 i L2 (np. planety lub Księżyca i Słońca) będzie:
|
PS = |
360°
 2 2 –  1 1 |
|
= |
τ1τ2
τ1 – τ2
|
. |
| (12) |
Okres (rok, miesiąc) anomalistyczny obejmuje czas
pomiędzy dwoma kolejnymi przejściami obiektu przez perycentum:
Okres (rok, miesiąc) gwiazdowy albo syderyczny dotyczy ruchu względem
układu inercjalnego (odległych gwiazd albo kwazarów) i mierzy się
czasem dwóch kolejnych przejść obiektu przez ten sam punkt
ekliptyki (np. punkt Barana) z danej jednej epoki (tj. bez precesji):
gdzie pA jest tzw.
ogólną precesją w długości i możemy tutaj przyjąć
wartość z teorii VSOP82: 5029,0966''T + 1,1137''T2 – 0,000076''T3 [9],
wyrażenie z systemu Międzynarodowej Unii Astronomicznej [10]:
5029,0966''T + 1,11161''T2 – 0,000113''T3,
albo bardziej rozbudowany wzór Laskara [6].
W literaturze możemy spotkać się też z terminami rok
zaćmieniowy lub miesiąc smoczy, które oznaczają średni okres
pomiędzy kolejnymi przejściami Słońca lub Księżyca przez węzeł
wstępujący orbity Księżyca:
gdzie ΩK z kropką jest pochodną po czasie ze średniej długości
węzła Księżyca a  pochodną średniej długości
Słońca (dla roku zaćmieniowego) lub Księżyca (miesiąc smoczy).
Oto podstawowe elementy średnie orbity Księżyca według rozwiązania
ELP-2000/85 teorii Chapront-Touzé i Chapront ([11], [12]):
pochodną średniej długości
Słońca (dla roku zaćmieniowego) lub Księżyca (miesiąc smoczy).
Oto podstawowe elementy średnie orbity Księżyca według rozwiązania
ELP-2000/85 teorii Chapront-Touzé i Chapront ([11], [12]):
|
LK = 218°18'59,95571'' + 1732564372,83264T
– 4,7763T2 + 0,006681T3
– 5,522·10–5T4 |
|
ΩK =
125°2'40,39816'' – 6962890,2656T + 7,4742T2 + 0,007702T3 –
5,939·10–5T4 |
gdzie współczynniki przy Tn podano w sekundach łuku (|T| < 35).
Dla przykładu obliczymy wyrażenie na długość roku zwrotnikowego.
Okres ten ma pewne znaczenie przy konstrukcjach zależnych od niego
kalendarzy słonecznych, chociaż w takich zastosowaniach lepiej
posługiwać się wprost długością ekliptyczną, o czym będziemy
jeszcze pisać. Przybliżone wartości liczbowe innych ze zdefiniowanych
okresów podajemy w poniższej tabelce.
|
Długości miesięcy (dla epoki J2000) i lat |
| Okres | Miesiąc | Rok |
| Zwrotnikowy (p. Barana – p. Barana) | 27,321582 | 365,2421897 – 6,16·10–6T |
| Gwiazdowy (gwiazda – gwiazda) | 27,321662 | 365,2563631 + 1,04·10–7T |
| Anomalistyczny (perygeum – perygeum) | 27,554550 | 365,2596359 + 3,17·10–6T |
| Smoczy/zaćmieniowy (węzeł – węzeł) | 27,212221 | 346,6200759 + 3,24·10–5T |
| Synodyczny (nów – nów) | 29,530589 |
| |
Wyniki podano w dobach, przy czym jeśli występuje T to
należy je wyrazić w wiekach juliańskich od J2000. Wartości takie
uzyskaliśmy zgodnie z opisem w tekscie i używając elementów średnich
teorii Bretagnona [4] oraz Chapront-Touzé i Chapront [11].
Nie podajemy zmian długości miesięcy, gdyż są one bardzo powolne.
Najszybsza zmiana (skracanie miesiąca anomalistycznego) wynosi
1,04·10–6 doby na wiek, tj. mniej niż 0,1 sekundy na wiek.
|
|
Podstawiając współczynniki występujące w
równaniu (1) do pierwszego ze wzorów (11) dostajemy
(w wiekach juliańskich!):
|
τ = |
360·3600
129602771,36329 + 2·1,093241·T +
3·0,0000762·T2
|
, |
|
gdzie czynnik 3600 zamienia jednostki współczynników  z sekund łuku na stopnie. Mnożąc to wyrażenie przez 36525 (w celu
zamiany wyniku z wieków juliańskich na doby) i upraszczając
współczynniki liczbowe dostajemy ostatecznie
z sekund łuku na stopnie. Mnożąc to wyrażenie przez 36525 (w celu
zamiany wyniku z wieków juliańskich na doby) i upraszczając
współczynniki liczbowe dostajemy ostatecznie
|
τ = |
36525·360·3600
129602771,36329 + 2,186482·T + 0,0002286·T2
|
|
|
|
≈ 365,242189669781
– 6,161870·10–6·T –
6,44·10–10·T2. |
| (16) |
Przybliżenie powyższe jest jedynie formalnością, gdyż
na przedziale 10 000 lat wynikający stąd błąd długości
roku nie przekracza 0,0001 sekundy czasu — grubo poniżej błędu
wynikającego z niepewności długości ekliptycznej Słońca.
Otrzymany wynik można porównać ze wzorem Newcomba (opartym na jego
teorii ruchu Ziemi, a w szczególności na wyrażeniu na średnią
długość Słońca) cytowanym powszechnie w podręcznikach:
|
τN = 365,24219879 – 6,14·10–6·T'
= 365,24219265 – 6,14·10–6·T, |
|
gdzie T' = T + 1 liczone jest od epoki J1900. Wynik taki dostalibyśmy
przyjmując za Newcombem na średnią długość Słońca
|
LN = 279°41'48,04'' + 129602768,13''T' + 1,089''T'2. |
|
Zauważamy, że te dwie długości roku zwrotnikowego, obliczona przez
nas i przez Newcomba, współcześnie różnią się o 0,26 s przy
porównywalnych zmianach wiekowych (skracanie roku o 0,00000616d = 0,53s
na wiek).
Widzieliśmy, że nasz wzór (16) na długość roku
zwrotnikowego,
który zastępuje uhonorowany wieloletnim stosowaniem wzór newcombowski, w
sposób oczywisty wyraża rok w standardowych dobach po 86 400 sekund SI.
Są to zatem jednostki absolutne, niezależne od zmiennej dobowej rotacji
Ziemi. Także wzór Newcomba był niezależny od rotacji Ziemi (chociaż
za czasów Newcomba nie było pojęcia czasu efemeryd, to dziś jego
formuły interpretujemy jako wyrażone w jednostkach tego właśnie czasu,
a więc praktycznie takich samych jak nasze, tj. z układu SI).
Wspominamy tutaj o tym ze względu na Hope, który
przekonywująco dowodził [3], że występujący we
wzorze Newcomba składnik –6,14·10–6·T'
wynika li tylko ze zwalniania rotacji Ziemi. Ponieważ tak się składa, że
wydłużanie się doby można błędnie zinterpretować jako skracanie
roku w stopniu porównywalnym z tym wynikającym z nieliniowości zmian
długości ekliptycznej, sądzić trzeba, iż właśnie tutaj tkwi
źródło nieporozumienia.
Sumowanie długości roku zwrotnikowego a
kalendarz słoneczny
Jak wspomnieliśmy we Wstępie, w niektórych analizach kalendarzy
słonecznych w celu obliczenia ilości
lat zwrotnikowych w zadanym okresie sumuje się długości roku
zwrotnikowego. I chociaż wyniki liczbowe są zwykle poprawne (z pewną
tolerancją), to jednak jest to niewłaściwa metoda opierająca się
na fakcie, że zmiany długości roku są rzeczywiście bardzo małe.
Dla poparcia tej opinii załóżmy, że długość ekliptyczna jest
wyrażona w formie L = t + ε(t), gdzie t jest czasem liczonym
w latach o stałej długości (np. po 365,25 dób). Wtedy różnica
czasów mierzonych w latach zwrotnikowych i stałych wyniesie dokładnie
Gdybyśmy zliczali lata zwrotnikowe, każde o długości
|
τ = |
1
|
= |
1
|
1+ |
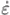 (t) (t) |
|
≈ 1 – |
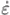 (t) (t) |
|
(zakładając, że 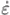 << 1), dostalibyśmy
<< 1), dostalibyśmy
|
N'' = |
∫ |
t
0
|
τ dt – t ≈ |
∫ |
t
0
|
[1 – |
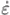 (t)]dt – t = –ε(t).
(t)]dt – t = –ε(t). |
|
Oznacza to, że całkowanie okresu, τ, tj. sumowanie długości
lat zwrotnikowych, prowadzi do prawie takich samych wyników przy
zmienionym znaku. Ten rezultat jest intuicyjnie zadowalający, jednak
dosadniej przekonuje następujące rozumowanie:
gdyby rok miał stałą długość ale był nieco, mówmy o δ,
krótszy niż rok kalendarzowy, wtedy po q kalendarzowych latach byłoby
w przybliżeniu q + qδ lat zwrotnikowych, nie zaś
q – qδ, jak to wynikałoby z samego sumowania długości lat.
Zauważamy łatwo, że w przypadku roku o stałej długości analizowany
okres czasu należałoby raczej podzielić przez długość roku
zwrotnikowego, by wyrazić go w tych jednostkach, co efektywnie prowadzi do
wykorzystania odwrotności okresu albo prędkości orbitalnej.
Trzeba także pamiętać, że dokładność obliczenia N'' zależy
od małości składnika 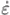 (t) tak, że w ogólności
należałoby unikać sumowania lat zwrotnikowych i używać bezpośrednio
średniej długości ekliptycznej w analizach kalendarzy — tak,
jak to opisaliśmy wcześniej.
(t) tak, że w ogólności
należałoby unikać sumowania lat zwrotnikowych i używać bezpośrednio
średniej długości ekliptycznej w analizach kalendarzy — tak,
jak to opisaliśmy wcześniej.
O pewnej formule kalendarzowej
Peck w swojej pracy [2] wyprowadził dwa nowe dość ogólne wzory
polecając je do stosowania w analizach kalendarzy słonecznych. Autor
ten, jak już wspominałem, oparł się na krytykowanym tutaj podejściu
i nie uwzględnił zmiennej rotacji Ziemi. Jeden z tych wzorów mówi
ile lat przestępnych, l, powinien mieć dowolny kalendarz słoneczny
w q latach liczonych od początku naszej ery, tj. od 0 r.n.e.
(JD = 1721058):
|
lP = 0,24231545q –
3,07·10–8q(q + 1). |
|
Nie jest zbyt trudno zauważyć, że wielkość
n(T) – 365·Lτ(T),
tj. różnica między ilością obrotów Ziemi (dni) i ilością
dni w Lτ 365-dniowych latach (chcemy by ilość
lat kalendarzowych była dokładnie równa ilości lat zwrotnikowych,
Lτ), jest poszukiwaną ilością lat przestępnych
między epokami J2000 i T. Przesuwając początek liczenia lat
przestępnych na rok 0 (dla T = –730487/36525
≡ To) dostajemy natychmiast w sposób ścisły:
|
|
|
|
n(T) – n(To)
– 365·[Lτ(T) –
Lτ(To)] |
| (17) | |
|
| 484,504 + 24,2195·T
– 3,079·10–4T2
– 2,15·10–8T3 – |
ΔT
– ΔT'o
86400
|
, |
|
|
gdzie ΔT'o jest wartością ΔT w roku 0
(albo dla epoki To).
W celu porównania naszego wzoru z Peckowym musimy zamienić argument T
na q. Z zadowalającym przybliżeniem T = q·365,2422/36525 + To,
zatem
|
l = q[0,242313 – q(3,07·10–8
+ 2,15·10–14q)] – |
ΔT –
ΔT'o
86400
|
, |
| (18) |
gdzie teraz argumentem jest rok naszej ery, q. Czytelnik może tą
wielkość porównać
z liniowo narastającą ilością lat przestępnych w kalendarzu
gregoriańskim: 97 na 400 lat (lG = 0,2425q).
Warto jeszcze zauważyć, że l można wyrazić także ściśle w funkcji
q przez podstawienie T = (365q + l)/36525 + To do (17), a
następnie rozwiązanie powstałego równania trzeciego stopnia względem
l. Tego rozwiązania nie prezentujemy z powodu jego złożoności i
faktu, że przybliżenie (18) na przedziale lat od 0 do 12 000 nie
odbiega od niego więcej niż o 0,002 dnia.
Odejmując od równania (18) ilość lat przestępnych faktycznie
wprowadzonych w określonym kalendarzu słonecznym do roku q dostajemy
uogólnienie drugiego z kalendarzowych wzorów Pecka (równanie
(3) w [3]), które mówi o błędzie tego kalendarza w stosunku do
idealnego kalendarza słonecznego. Porównując nasze uogólnienia
z oryginałami zauważamy, że istotną praktyczną różnicą
jest jedynie przyczynek ΔT, gdyż na przestrzeni stosowalności
tych wzorów (ok. 10 000 lat) pozostałe różnice są zaniedbywalne.
Podsumowanie
W przedstawionym artykule starałem się pokazać, że nasz
obecny kalendarz jest bardzo dobrym przybliżeniem idealnego kalendarza
naturalnego liczącego lata zwrotnikowe i że będzie tak jeszcze przez
kilka tysięcy najbliższych lat. Krytycznie oceniłem spotykane przymiarki
do reformy kalendarza greogoriańskiego jako nie mające solidnych podstaw.
Główne tezy krytyki są następujące.
Po pierwsze, dostępne wyrażenia na długość ekliptyczną Słońca
tracą swoją ważność po 3 – 10 tysiącach lat od
współczesności. Po drugie, zmienna szybkość rotacji Ziemi
uniemożliwia precyzyjne przewidywanie ilości dni kalendarzowych
(określanych odstępem czasu między kolejnymi górowaniami Słońca)
w roku zwrotnikowym — do tego stopnia, że za 10 000 lat mamy już
niepewność (ostrożnie oceniając) 4 dni. Po trzecie wreszcie,
zgodności kalendarza cywilnego z rachubą astronomicznie ścisłą nie
powinno się analizować przez porównywanie średniej długości roku
zwrotnikowego i roku kalendarzowego, lecz raczej ich matematycznej
odwrotności — orbitalnej prędkości kątowej Słońca i czegoś, co
moglibyśmy nazwać ,,słońcem kalendarzowym".
Podaliśmy też kilka praktycznie użytecznych wzorów na obliczanie:
♦ ilości lat zwrotnikowych upływających do wskazanej epoki — wzór (3),
♦ o ile dni kalendarz gregoriański wyprzedza astronomiczny — (7),
♦ długości roku zwrotnikowego — (16), oraz
♦ ilości lat przestępnych,
jakie powinny wystąpić do wskazanego roku naszej ery w dowolnym kalendarzu
słonecznym, aby był on zgodny z porami roku — (17) lub (18).
[1] F.R. Stephenson, Liu Baolin, The Observatory, 111, 21 (1991).
[2] P.A. Peck, J. Roy. Astron. Soc. Can., 84, 14 (1990).
[3] E.R. Hope, J. Roy. Astron. Soc. Can., 58, 3 (1964).
[4] P. Bretagnon, Astron. Astrophys., 114, 278 (1982).
[5]
K.M. Borkowski, J. Roy. Astron. Soc. Canada, 85, No. 3, 121, (1991).
[6] J. Laskar, Astron. Astrophys., 157, 59 (1986).
[7] D.D. McCarthy, A.K. Babcock, Phys. Earth Planet. Interiors, 44,
281 (1986).
[8] F.R. Stephenson, L.V. Morrison, Phil. Trans. Roy. Soc. London,
A313, 47 (1984).
[9] P. Bretagnon, J. Chapront, Astron. Astrophys., 103, 103 (1981).
[10] The Improved IAU System, Supplement to The Astronomical
Almanac 1984, U.S. Government Printing Office, Washington, and Her Majesty's
Stationery Office, London (1983), s. S1-S39.
[11] M. Chapront-Touzé, J. Chapront, Astron. Astrophys.,
190, 342 (1988).
[12] Connaissance des Temps. Éphémérides
Astronomiques, 1991, Bureau des Longitudes, Paris (1990).
File translated from
TEX
by
TTH,
version 3.12 on 30 Jul 2002.


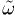 —
ekliptyczną
długością wstępującego węzła orbity zwiększoną o kątową
odległość peryhelium od węzła, T — czasem liczonym zwykle w
stuleciach juliańskich od epoki standardowej, a współczynniki
a, b, c i ewentualnie dalsze podaje się w stopniach lub sekundach łuku.
Z długości ekliptycznych (10) można łatwo obliczyć kilka
różnych okresów (w przypadku orbity Ziemi mówimy o latach, a o
miesiącach dla Księżyca).
—
ekliptyczną
długością wstępującego węzła orbity zwiększoną o kątową
odległość peryhelium od węzła, T — czasem liczonym zwykle w
stuleciach juliańskich od epoki standardowej, a współczynniki
a, b, c i ewentualnie dalsze podaje się w stopniach lub sekundach łuku.
Z długości ekliptycznych (10) można łatwo obliczyć kilka
różnych okresów (w przypadku orbity Ziemi mówimy o latach, a o
miesiącach dla Księżyca).
 oznacza pochodną po czasie (T) z L, zaś 360°
umieściliśmy w liczniku przy założeniu, że a, b, c, ...
wyrażono w stopniach; jeśli współczynniki te dane są w sekundach
łuku, wtedy w liczniku piszemy 360·3600'' — tak, jak w przykładzie
przy końcu tego punktu.
oznacza pochodną po czasie (T) z L, zaś 360°
umieściliśmy w liczniku przy założeniu, że a, b, c, ...
wyrażono w stopniach; jeśli współczynniki te dane są w sekundach
łuku, wtedy w liczniku piszemy 360·3600'' — tak, jak w przykładzie
przy końcu tego punktu.
 pochodną średniej długości
Słońca (dla roku zaćmieniowego) lub Księżyca (miesiąc smoczy).
Oto podstawowe elementy średnie orbity Księżyca według rozwiązania
ELP-2000/85 teorii Chapront-Touzé i Chapront ([11], [12]):
pochodną średniej długości
Słońca (dla roku zaćmieniowego) lub Księżyca (miesiąc smoczy).
Oto podstawowe elementy średnie orbity Księżyca według rozwiązania
ELP-2000/85 teorii Chapront-Touzé i Chapront ([11], [12]):
 z sekund łuku na stopnie. Mnożąc to wyrażenie przez 36525 (w celu
zamiany wyniku z wieków juliańskich na doby) i upraszczając
współczynniki liczbowe dostajemy ostatecznie
z sekund łuku na stopnie. Mnożąc to wyrażenie przez 36525 (w celu
zamiany wyniku z wieków juliańskich na doby) i upraszczając
współczynniki liczbowe dostajemy ostatecznie
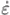 << 1), dostalibyśmy
<< 1), dostalibyśmy
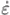 (t) tak, że w ogólności
należałoby unikać sumowania lat zwrotnikowych i używać bezpośrednio
średniej długości ekliptycznej w analizach kalendarzy — tak,
jak to opisaliśmy wcześniej.
(t) tak, że w ogólności
należałoby unikać sumowania lat zwrotnikowych i używać bezpośrednio
średniej długości ekliptycznej w analizach kalendarzy — tak,
jak to opisaliśmy wcześniej.