| Ui = U(Ti) – U(0) = Umax |  |
| – |
|  | . |
ANALIZA CHARAKTERYSTYK WZMOCNIENIA ODBIORNIKA PRZEŁĄCZANEGO
Katedra Radioastronomii Uniwersytetu M. Kopernika (Toruń)
(Otrzymano 15 lutego 1980 r.)
| S t r e s z c z e n i e — Praca stanowi doświadczalną weryfikację proponowanego przez autora analitycznego opisu charakterystyki wzmocnienia odbiornika przełączanego z ARW. Analiza wyników potwierdza słuszność sugerowanego podejścia i pozwala zdecydowanie odrzucić wcześniejsze przypuszczenie o logarytmicznym wzmocnieniu odbiornika. |
| AN ANALYSIS OF THE NONLINEAR GAIN OF A SWITCHED RECEIVER. S u m m a r y — A new formula for a Dicke receiver with an AGC was tested against experimental data. The analysis confirms validity of theoretical considerations by this author and allows to decisively reject an earlier assumption about the logarithmic gain of the receiver. |
Jednym z problemów obserwacji Słońca na falach metrowych jest trudność zapewnienia dużej dynamiki odbiorników (B o r k o w s k i i in. 1980). Częstym rozwiązaniem bywa zastosowanie wzmacniaczy logarytmicznych, dzięki którym napięcie wyjściowe odbiornika jest proporcjonalne do logarytmu sygnału wejściowego (mierzonego). W przypadku odbiorników nieprzełączanych tego typu charakterystykę wzmocnienia można uzyskać poprzez automatyczną regulację wzmocnienia (ARW) wzmacniaczy wielkiej lub pośredniej częstości. Zastosowanie ARW w odbiorniku przełączanym (Dicke'go) powoduje, że jego charakterystyka wzmocnienia różni się zdecydowanie od logarytmicznej (B o r k o w s k i 1980). Zignorowanie tego faktu może prowadzić do ogromnych błędów w pomiarach — zwłaszcza w pomiarach promieniowania Słońca aktywnego. Wiąże się to z tym, że w praktyce obserwacyjnej często charakterystykę wzmocnienia doświadczalnie można określić tylko dla niewielkich sygnałów, a przy pomiarach sygnałów wielokrotnie większych znaną część charakterystyki ekstrapoluje się w górę.
Niniejsza praca ma na celu doświadczalne zweryfikowanie teoretycznej analizy charakterystyki wzmocnienia odbiornika przełączanego z ARW, którą przeprowadziłem wcześniej (B o r k o w s k i 1980). Z tamtej pracy wynikało, że jeśli tylko wzmocnienie w pętli ARW takiego odbiornika jest dostatecznie duże i można zaniedbać nieidealność przełącznika wejściowego oraz detektora obwiedni, to napięcie wyjściowe U powinno wiązać się z temperaturą antenową TA i równoważną temperaturą źródła porównawczego (sygnału odniesienia) Tr za pomocą wzoru:
| (1) |
gdzie: n charakteryzuje detektor i przyjmuje wartość 1 w przypadku detektora liniowego, a wartość 2 — kwadratowego, zaś Umax jest pewną stałą proporcjonalności.
Sprawdzenie zasadności wzoru (1) przeprowadzę dla dwóch wspomnianych już przypadków odbiornika przełączanego: z detektorem liniowym i kwadratowym. Oprę się przy tym na kilkuletnich danych wziętych z codziennych kalibracji toruńskiego odbiornika pracującego w systemie do obserwacji Słońca na częstości 127 MHz (B o r k o w s k i i in. 1975). Kalibracje takie odbywają się przez zastąpienie sygnału antenowego sygnałem ze skalibrowanego generatora szumów. Już samo podłączenie generatora w miejsce anteny jest równoznaczne z podaniem sygnału kalibracyjnego na wejście odbiornika. W przypadku dopasowania impedancji obu urządzeń sygnał ten ma moc widmową 1 kTo, gdzie To jest temperaturą otoczenia, a k — stałą Boltzmanna. Moc ta na wyjściu odbiornika odpowiada najniższemu poziomowi napięcia (prądu), dlatego wygodnie jest potraktować ją jako początek charakterystyki. W wyniku kalibracji dostaje się ciąg poziomów napięcia odpowiadających znanym mocom sygnału wejściowego: {Ui,Ti}, gdzie Ui = U(Ti) – U(0). W momencie, gdy generator szumów wytwarza sygnał o mocy odpowiadającej temperaturze Ti w odbiorniku przełączanym wzmacniany jest sygnał odpowiadający temperaturze (Ti + Tr)/2 + To/2 + TR, gdzie TR jest temperaturą szumową (nadwyżkową) samego odbiornika.
Jeżeli impedancja generatora szumów (anteny) jest inna niż impedancja wejściowa odbiornika, to mniej mocy zostanie wydzielonej w obwodach wejściowych odbiornika niż w przypadku dupasowania. Niech straty takie charakteryzuje współczynnik ε, przyjmujący wartość z przedziału [0,1]. Wtedy sygnał TA wyrażony w jednostkach kTo i występujący we wzorze (1) przyjmuje postać:
| (2) |
Podobnie przypisanie źródłu sygnału porównawczego niedopasowania, powodującego. straty odpowiadające współczynnikowi ε', pozwala wyrazić moc dostarczaną do odbiornika z tego źródła przez:
| (3) |
gdzie T′r jest dostępną mocą generowaną w źródle porównawczym (tzn. taką, którą można by zeń czerpać w warunkach idealnego dopasowania). Występujące we wzorze (3) T′R wyraża fakt, że własności szumowe odbiornika mogą się zmieniać wskutek zmiany obciążenia (zmiana warunków pracy obwodów wejściowych). Gwoli ścisłości trzeba także dodać, że TR w wyrażeniu (2) należy traktować jako temperaturę szumową odbiornika właściwą niedopasowamu określającemu ε. Zagadnienie powiązania napięć Ui zmierzonych na wyjściu odbiornika z sygnałami Ti podawanymi z generatora szumów prowadzi w ogólności do niezbyt użytecznej w praktyce zależności:
|
Jeśli jednak T'r = 1 (źródło porównawcze umieszczone w temperaturze otoczenia, tak jak w toruńskim systemie odbiorczym) i ε′ = ε (a zatem także T′R = TR), to owa zależność znakomicie upraszcza się i staje się rownoważna wzorowi:
|
(4) |
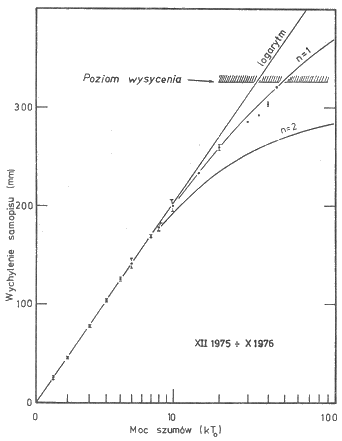 |
| Rys. 1. Charakterystyka odbiornika przełączanego z ARW i detektorem liniowym (n = 1). Pokazano też najlepsze dopasowania funkcji logarytmicznej i charakterystyki teoretycznej odbiornika z detektorem kwadratowym (n = 2) |
który z kolei w dwóch szczególnych przypadkach: gdy n = 1 lub n = 2, łatwo przekształca się ostatecznie do postaci:
| (5) |
gdzie A jest pewną stałą zależną od parametru n, temperatury szumowej odbiornika TR, współczynnika ε i napięcia Umax.
W celu wyznaczenia charakterystyki wzmocnienia odbiornika wystarczy teraz dobrać tylko dwa parametry we wzorze (5): A i Umax (zakłada się, że parametr n jest znany). Kilka praktycznie użytecznych sposobów dopasowania wyników pomiarów do tego wzoru opisałem w Dodatku.
Charakterystykę toruńskiego odbiornika w okresie XII 1975 – X 1976 r. sporządziłem przez uśrednienie nieco ponad 200 wybranych pomiarów z przedziału temperatur generatora szumów 0 – 45 To. W tym czasie do kalibracji używano generatora typu BM-380E (produkcji CSRS). Do wyników pomiarów dopasowałem funkcję logarytmiczną za pomocą programu na kalkulator HP-25, opublikowanego w opracowaniu Hewlett-Packard (1976) oraz charakterystyki teoretyczne typu (5) (Dodatek). Liczbowe wyniki tych dopasowań zawiera tab. 1, a na rys. 1 naniosłem odpowiednie przebiegi graficzne, przy tym wartości doświadczalne są tam zaznaczone punktami. Ponieważ odstępstwa wyników doświadczalnych od funkcji dopasowanych rosną ze wzrostem sygnału, dopasowania ograniczyłem tylko do dolnych obszarów charakterystyki odbiornika. Dzięki temu zabiegowi lepiej widać, która funkcja lepiej odzwierciedla rzeczywistość.
Wielkość Jedn. Wyniki pomiarów lub obliczeń Sygnał (Ti) kTo 0,5 1 2 3 4 5 7 8 10 15 20 30 35 40 45 Wychyl. samopisu (Ui) mm 25 45,5 77,5 103 125 141 170 178 200 233 260 286 293 304 320 Ilość pomiarów - 39 8 87 6 2 49 3 4 4 1 5 1 1 4 1 Ocena rozrzutu mm 2 1 1,5 1,5 2 5 1 4 6 - 3 - - 2 - -2 + 2,01·10Ui/260,9 kTo 0,50 1,00 1,98 2,99 4,05 4,97 7,00 7,66 9,73 13,7 17,9 23,1 24,7 27,4 31,8 1 4878Ui/(511,8 - Ui)2 kTo 0,51 1,02 2,00 3,01 4.08 5,00 7,10 7,79 10,04 14,6 20,0 27,4 29,9 34,4 42,4 2 4619Ui/(503,1 - Ui)2 kTo 0,51 1,00 1,98 2,97 4,04 4,97 7,08 7,78 10,06 14,8 20,3 28,0 30,7 35,4 44,1 3 5,54Ui/(300,3 - Ui) kTo 0,50 0,99 1,93 2,98 3,95 4,90 7,23 8,1 11,0 19,2 35,7 111 222 - - |
Wielkość Jedn. Wyniki pomiarów lub obliczeń Sygnał (Ti) kTo 1 1,5 2 3 4 5 7 10 15 20 30 45 Wychylenie samopisu (Ui) mm 46 62 74,5 93,5 106,5 117 134 147 162 165 176 183 Ilość pomiarów - 18 3 58 18 14 30 4 21 4 10 1 28 Ocena rozrzutu mm 1 1 1,5 1,5 2 2 3 3 3 4 - 5 0,641·10Ui/125,7 - 0,5 kTo 0,99 1,50 2,01 3,05 4,01 4,96 6,96 8,97 12,0 12,7 15,6 17.8 la 3,544Ui/(197,36 - Ui) kTo 1,08 1,62 2,15 3,19 4,15 5,16 7,50 10,3 16,2 18,1 29,2 45,2 3 3,215Ui/(194,06 - Ui) kTo 1,00 1,51 2,00 2,99 3.91 4,88 7,17 10,0 16,2 18,3 31,3 53,2 2 879,92Ui(255,6 - Ui)2 kTo 0,92 1,46 2;00 3,13 4,22 5,36 7,97 11,0 16,3 17,7 24,4 30,5 |
Rysunek 1 jednoznacznie podpowiada, że do wyników pomiarów najlepiej pasuje charakterystyka teoretyczna, odpowiadająca odbiornikowi przełączanemu z liniowym detektorem obwiedni. Jednakże i ona już dla sygnałów większych od 20 do 30 kTo w sposób zdecydowany odbiega od tych wyników. Zwraca też uwagę bardzo dobra zgodność wszystkich (!) dopasowywanych funkcji z wartościami doświadczalnymi w zakresie temperatur od 0 do ok. 7 To. Ponieważ średnie napięcie wyjściowe detektora w odbiorniku z ARW zachowuje się tak, jak funkcja logarytmiczna (por. wykres przedstawiony u B o r k o w s k i e g o i in. 1975), to wyżej odnotowana zgodność w przeszłości tylko utwierdziła mylne mniemanie, że charakterystyka wzmocnienia analizowanego tutaj odbiornika powinna być logarytmiczną. O tej mylności jeszcze dobitniej przekona następny przykład.
Zbliżoną do teoretycznej odbiornika przełączanego z ARW i z detektorem kwadratowym (n = 2) jest charakterystyka odbiornika toruńskiego z okresu 16 XI 1974 – 30 IV 1975 r. (różne charakterystyki tego samego odbiornika były rezultatem zmian konstrukcyjnych towarzyszących usuwaniu awarii urządzenia). Jest ona przedstawiona w tab. 2 i na rys. 2 wraz z wynikami dopasowań wykonanych w taki sam sposób, jak w pierwszym przykładzie. Łatwo dostrzec, że ta charakterystyka znacznie lepiej pasuje do teoretycznej niż w przypadku z detektorem liniowym. Tym samym znajduje tutaj potwierdzenie przewidziana teoretycznie (B o r k o w s k i 1980) większa wrażliwość odbiornika z detektorem liniowym na niedoskonałości niektórych podzespołów.
W celu sprawdzenia słuszności założenia o idealnej liniowości detektora z pierwszego przykładu oraz w nadziei, że dopasowania będą znacząco lepsze, wykonałem próbę dobrania trzech — a nie jak dotąd dwóch — parametrów charakterystyki teoretycznej. Posługując się wzorem (4) uwolniłem także parametr n i dopasowałem wyniki pomiarów (te, które zostały wykorzystane w przykładzie w Dodatku — tab. 4) metodą najmniejszych kwadratów na maszynie Riad-32 za pomocą programu GLSQA z biblioteki ASTRLIB (W o l s z c z a n i L u d w i c h o w s k i 1979). Okazało się, że najlepiej pasujące n mało różniło się od jedności, a różnicę (ok. 3%) nietrudno spisać na karb błędów pomiarów.
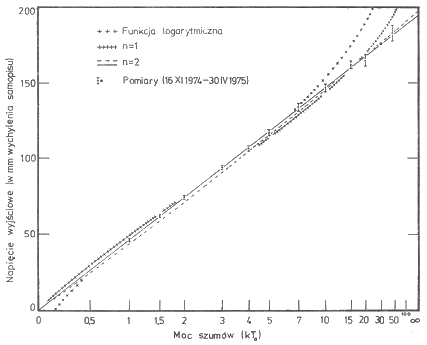 |
| Rys. 2. Charakterystyka odbiornika przełączanego z ARW i detektorem kwadratowym (n = 2). Linią ciągłą zaznaczono najlepsze dopasowanie wykonane metodą linearyzacji (program 3 ), zaś przerywaną — metodą najmniejszych kwadratów (program 1a). Przedstawiono też najlepsze dopasowania innych funkcji |
W latach 1974–1978 strumienie promieniowania Słońca obliczano w Toruniu przez liniowe odcinkami przybliżanie rzeczywistej charakterystyki odbiornika, odzyskanej z bieżących kalibracji w zakresie 0 – 8 kTo. Powyżej 8 kTo ekstrapolowano charakterystykę rzeczywistą z dolnych jej obszarów przez graficzne dopasowanie do funkcji logarytmicznej (w górnych partiach na ogół "naciągane" gdyż, jak to widać z obu rysunków, funkcja logarytmiczna zdecydowanie nie pasuje do charakterystyki rzeczywistej). Prowadziło to więc do systematycznego zaniżania wyników w sposób nieliniowy — tym bardziej im większy obserwowano strumień. W skrajnych przypadkach, w pobliżu poziomu "wysycenia", zaniżenie wyników mogło sięgać nawet kilku rzędów wielkości.
W podsumowaniu można stwierdzić, że przeprowadzona analiza charakterystyki toruńskiego odbiornika potwierdza słuszność wniosków teoretycznych wywiedzionych w mojej wcześniejszej pracy (B o r k o w s k i 1980). W przypadku odbiornika z detektorem kwadratowym całkowicie wystarczające okazuje się przybliżenie, w którym zaniedbuje się nieidealność przełącznika wejściowego, detektora obwiedni i skończoność wzmocnienia w pętli ARW. Takie przybliżenie jest natomiast niezadowalające przy analizie charakterystyki odbiornika z detektorem liniowym. Warto też zapamiętać, że stosunkowo złożona w ogólnym przypadku metoda najmniejszych kwadratów w rozpatrywanych problemach z powodzeniem może być zastąpiona uproszczeniem, polegającym na linearyzacji funkcji dopasowywanej.
Dopasowywanie charakterystyk teoretycznych odbiornika przełączanego do wyników kalibracji
Wszystkie niżej przedstawione algorytmy opracowałem pod kątem zastosowania do obliczeń na programowanym kalkulatorze HP-25. Do opisu metody najmniejszych kwadratów dołączyłem również szczegółowy opis programu, gdyż ograniczona pamięć kalkulatora może stanowić kłopotliwy problem przy próbach ułożenia innej wersji programu. Podobne opisy pozostałych (wraz z pewnymi pomocniczymi) programów można znaleźć w mojej pracy doktorskiej (B o r k o w s k i 1979).
a) Dopasowania ntetodą najmniejszych kwadratów (programy 1 i 1a)
Niech będzie dana funkcja T(U, Uo, A), gdzie Uo i A są pewnymi stałymi, oraz ciąg wyników doświadczalnych {Ti,Ui}. Dopasowanie funkcji T do wyników metodą najmniejszych kwadratów polega na dobraniu takich Ůo = Uo – ΔU i Ă = A – ΔA, dla których wyrażenie Σ[T(Ui,Ůo + ΔU,Ă + ΔA) – Ti]2 przyjmuje najmniejszą wartość. Jeżeli ten warunek uda się spełnić, to założenie, że T(U,Uo,A) = T(U, Ůo,Ă) + (∂T/∂Uo)ΔU + (∂T/∂A)ΔA (oznaczające, że ΔU i ΔA są małe) pozwala napisać układ równań:
|
który jest liniowy ze względu na ΔU i ΔA. W szczególności, jeśli T = AU/(Uo – U)k, to powyższy układ sprowadza się do układu:
|
gdzie dla przejrzystości opuszczono wskaźniki przy danych doświadczalnych (Ti i Ui)' po których następują sumowania. Z tych równań łatwo znajduje się poprawki do wstępnie przyjętych parametrów (Ůo i Ă):
ΔA = – Ă + (S2S5 – S3S4)/(S22 – S1S3) oraz
ΔU = (S1S5 – S2S4)/(S22 – S1S3) = [(Ă + ΔA)S1 – S4]/kĂS2,gdzie:
|
Mie- Instrukcja Uwagi Zawartości rejestrów jsce po obliczeniach 1 ÷ 2 f Last X X - ΔU 3 g x2 4 RCL 1 R0 - Uo 5 f Last X R1 - kĂ 6 - R2 - S2 7 STO 7 R3 - S3 8 6 lub 4 R4 - S4 9 f yx R5 - S5 10 ÷ R6 - S1 11 STO + 3 S3 R7 - kA 12 RCL 7 13 × 14 STO + 2 S2 15 f Last X Korzystanie z programu 16 × 17 STO + 6 S1 1. Wpisać program 18 × 19 RCL 7 lub g NOP 2. W stanie RUN wykonać: 20 × lub g NOP f PRGM, f REG 21 STO + 5 S5 22 RCL 7 3. Wprowadzić wstępne 23 × parametry: 24 STO + 4 S4 Ă, E↑, k, ×, 25 RCL 2 STO 1, Ůo, STO 0 26 RCL 5 27 × 4. Obliczyć poprawkę ΔU 28 RCL 4 i nową wartość kA: 29 RCL 3 T1, E↑, U1, R/S, 30 × T2, E↑, U2, R/S, 31 - .............., 32 RCL 2 TN, E↑, UN, R/S 33 g x2 34 RCL 6 5. Jeżeli poprawka ΔU jest 35 RCL 3 duża lub A dużo różni 36 × się od Ă to, utrzymując 37 - w rejestrze X ostatnio 38 g x≠0 obliczone ΔU, wykonać: 39 ÷ RCL 0, +, RCL 7, 40 STO 7 f REG, STO 1, R↓, 41 STO + 7 kA STO 0 42 RCL 6 i powtórzyć czynności 4. 43 × 44 RCL 4 45 - 46 RCL 2 47 ÷ 48 RCL 1 49 ÷ |
Program 1 (Tab. 3) służy do obliczania poprawek ΔA i ΔU w przypadku, gdy k = 2 (odbiornik z detektorem liniowym). Niewielka modyfikacja tego prograrnu w miejscach 8, 19 i 20 (w sposób podany w kolumnie "Uwagi") czyni wersję pozwalającą dopasowywać omawianą funkcję z parametrem k = 1 (odbiornik z detektorem kwadratowym; program 1a).
b) Dopasowania przybliżone (programy 2 i 3)
Związek T = AU/(Uo – U)2 można napisać w postaci √{U/T} = Uo/√A – U/√A. Położenie teraz y = √{U/T} pozwala zagadnienie dopasowania sprowadzić do przypadku regresji liniowej ciągu {yi,Ui}, gdzie yi = √{Ui/Ti}. Powszechnie znane wzory na parametry dopasowanej funkcji liniowej w tym przypadku sprowadzają się łatwo do poszukiwanych parametrów charakterystyki odbiornika:
|
gdzie symbol <x> oznacza wartość średnią wyników pomiaru wielkości x. Algorytm ten został wykorzystany przy układaniu programu 2.
Podobnie podstawienie y = 1/T i x = 1/U zastosowane do funkcji T = AU/(Uo – U), ponownie prowadzi do prostego zagadnienia dopasowania funkcji liniowej: y = –1/A + xUo/A. Tak jak w pierwszym przypadku, zastosowanie teraz metody najmniejszych kwadrat6w pozwala odzyskać poszukiwane parametry:
|
Program 3 ułożono zgodnie z takim algorytmem.
c) Przykład
Dnia 27 lutego 1979 r. wykonano kalibrację toruńskiego odbiornika na częstość 127 MHz za pomocą generatora szumów typu Γ2-32 (produkcji ZSRR). W tab. 4 są podane niektóre wyniki pomiaru napięcia wyjściowego Ui (w milimetrach wychylenia samopisu), uzyskanego pod wpływem sygnału Ti (w jednostkach kTo). Dopasowanie tych wyników do funkcji T = AU/(Uo – U)2 za pomocą programu 1 doprowadziło do parametrów i wartości obliczonych sygnałów podanych w trzecim wierszu tabeli. Dla porównania efektywności metody wykonano też dopasowanie tych samych wyników do tejże funkcji w oparciu o procedurę GLSQA (FORTRAN IV; W o l s z c z a n i L u d w i c h o w s k i 1979) na maszynie cyfrowej Riad-32. Rezultaty były identyczne.
W ostatnim wierszu tab. 4 podano wyniki dopasowania za pomocą programu 2.
1 Napięcie wyjściowe Ui (mm) 88,3 97 108,4 117 123,8 134 141,5 2 Sygnał Ti (kTo) 12 15 20 25 30 40 50 3 2629,7Ui/(227,8 - Ui)2 11,93 14,91 19,99 25,05 30,09 40,03 49,94 4 2678Ui/(228,8 - Ui)2 11,99 14,96 20,04 25,09 30,10 39,97 49,77 |
| LITERATURA |