| ΔT = T |  |
|  |
1/2
|
. |
POSTĘPY ASTRONOMII
Tom XXVIII (1980). Zeszyt 1, 15–34
Instytut Astronomii Uniwersytetu M. Kopernika (Toruń)
|
RADIO ASTRONOMY RECEIVERS Abstract In the paper basic concepts of noisy signal measurements are given. New formulae relating the output voltage to the input signal of a switched radiometer with an automatic gain control are developed. The receiver is shown to be relatively easily available and reliable tool for amateur radio astronomers. Finally some remarks about the Ryle-Vonberg system and its advantages are presented. |
Promieniowanie radiowe obiektów astronomicznych ma charakter szumowy. Zagadnienie jego pomiaru wiąże się zatem z detekcją zmian w poziomie szumów różnego pochodzenia, włącznie z szumami generowanymi przez sam system odbiorczy i odebranymi przez anteny z takich źródeł jak otoczenie, atmosfera i Galaktyka.
Moc szumów określa się zwyczajowo za pomocą tzw. równoważnej temperatury szumowej. To przedstawienie opiera się na znanej proporcjonalności mocy szumów termicznych dostępnych z opornika umieszczonego w temperaturze T (kelwinów) do tej temperatury (Z i e l 1954): P = kTΔf, gdzie k jest stałą Boltzmanna (1,38·10–23 J/K), a Δf — przedziałem częstości, w którym dokonuje się pomiaru mocy szumów (Hz).
Czułość systemu odbiorczego (najmniejszy wykrywalny sygnał) wiąże się ściśle z błędem pomiaru. Zależy ona od wielu czynników: charakterystyki anten, parametrów odbiornika, czasu pojedynczego pomiaru, ilości informacji odzyskiwanej równocześnie i wielkości obszaru nieba, który się obserwuje.
W literaturze zwykle podawane są wielce uproszczone analizy przetwarzania sygnałów w samym odbiorniku, co niekiedy prowadzi do błędnych wniosków. Najjaskrawszymi przykładami są chyba nieścisłości dotyczące czułości odbiorników, zauważone w cenionych dla innych powodów książkach N i k o l a e v a (1964), K r a u s a (1966) i E s e p k i n y i in. (1973), przez K i s l j a k o v a (1978; por. też K i s l j a k o v 1979 i K o r o l' k o v 1979). K i t t e l (1977) zwraca uwagę na brak jednoznacznego określenia częstości odniesienia przy definiowaniu równoważnej wstęgi szumowej w.cz.
Zagadnieniu pomiaru i detekcji sygnałów szumowych poświęcę znaczną część artykułu. W dalszej kolejności przedyskutuję szczegółowo niektóre aspekty odbiornika przełączanego z ARW. Wyróżnienie tego typu odbiornika wynika z dwóch, przynajmniej, przyczyn: wieloletniego użytkowania w toruńskiej służbie Słońca i braku rozważań teoretycznych na temat charakterystyki takiego odbiornika w dostępnej literaturze. W końcu pracy zwrócę uwagę na odbiornik Ryle'a-Vonberga i możliwości zbudowania odbiornika lepiej zaspokajającego wymagania wąskopasmowych obserwacji Słońca na falach metrowych.
Najprostszy odbiornik radioastronomiczny, albo przyrząd do pomiaru mocy szumów, składa się ze wzmacniacza wielkiej częstości (w.cz.), detektora i filtru wąskopasmowego. Niech na wejście takiego odbiornika będzie podany sygnał w postaci szumu normalnego (gaussowskiego) V z zerową średnią i jednostkową gęstością widmową mocy (<V2> = 1). Tenże sygnał pojawi się na detektorze, ale już z mocą widmową |A(f)|2, gdzie A(f) jest napięciową charakterystyką przenoszenia wzmacniacza w.cz. Zakładając, że detektor ma charakterystykę kwadratową, a sygnał podetekcyjny jest wygładzany za pomocą filtru o charakterystyce F2(f), na wyjściu odbiornika dostaje się sygnał v + <V2>, którego widmo jest proporcjonalne do:
| (1) |
gdzie pierwszy składnik określa widmo fluktuacji (v) (R i c e 1944), a drugi jest składową stałą proporcjonalną do mocy szumów wejściowych.
Miarą czułości instrumentu jest względna fluktuacja napięcia wyjściowego √(<v2>)/<V2>, którą można wyznaczyć ze składników wyrażenia (1). Zachodzi mianowicie:
| (2) |
gdzie współczynniki proporcjonalności są takie same dla obu związków. Przypisując powyższym mocom widmowym temperatury równoważne, odpowiednio: √(<v2>) ~ ΔT i <V2> ~ T, z (2) dostaje się:
| (3) |
Jeśli w (3) można przyjąć, że
|
to wzór ten uprości się do:
| (4) |
w wyrażeniu (4)
|
|
przy prostokątnej wstędze w.cz. o szerokości Δf, jest także równa tej szerokości; może być ona zatem definicją równoważnej szerokości wstęgi szumowej. Taką właśnie definicję zaproponował ostatnio K i t t e l (1977), dla celów termometrii. Skądinąd ta sama definicja była już zasadnie używana w radioastronomii, w równoważnych postaciach, w przeszłości (np. B r a c e w e l l 1962; T i u r i 1964; E s e p k i n a i in. 1973). W pracach radioastronomicznych nie odnotowano jednak przybliżenia w przejściu z zależności (3) do (4).
Często zamiast równoważnej szerokości wstęgi szumowej wygodniej jest posługiwać się wielkością odwrotną — równoważną stałą czasową τ = 1/ΔfLF. Wtedy wzór (4) można zapisać jako:
| (5) |
która to postać jest szeroko używana w praktyce. Okazuje się też, że wzór ten stosuje się również do odbiorników innych niż ten najprostszy, jednakże wówczas prawą stronę (5) należy pomnożyć przez czynnik zależny od konstrukcji odbiornika i metody pomiaru sygnału (jest to czynnik większy lub równy jedności). Także charakterystyka detektora nie jest krytyczna dla czułości systemu, np. w przypadku użycia detektora liniowego w miejsce kwadratowego prawą stronę wzoru (5) należy dodatkowo zwiększyć o 3–5% (C h r i s t i a n s e n, H ö g b o m 1969; E v a n s 1968). Niekiedy wielkość q = √(ΔfHFτ) nazywa się zyskiem radioastronomicznym, ponieważ, jak to widać z (5), oznacza on q-krotnie wyższą czułość systemu odbiorczego niż wynosi temperatura systemowa.
Czasami omawiany wzór na czułość odbiornika podawany jest w nieco innej postaci. Jednak na ogół różnice wynikają z różnic w przyjętych definicjach na równoważne szerokości wstęgi częstości. Spotyka się wszakże przypadki błędnej interpretacji zagadnienia czułości przyrządów pomiarowych. Należy podkreślić, że jeżeli już zgodziliśmy się na przybliżenie całki splotu inną wielkością, które na ogół jest rzeczywiście dobre, to wzór (5) określa najlepszą z osiągalnych czułości. W tym kontekście wzór przedstawiony przez P e p p e r a (1975) oraz P e p p e r a i B r o w n a (1979), a sugerujący, że czułość ich instrumentu do pomiaru temperatury przy pomocy pewnej nowej techniki jest lepsza o czynnik √π niż czułość (5), wypada uznać za wynik li tylko innego sensu przyjętych przez nich miar szerokości wstęg szumowych.
Zwrócę jeszcze uwagę na wspomniane już przybliżenie użyte w wyprowadzeniu zależności (5). Ocenę zasadności przybliżenia łatwo jest przeprowadzić w przypadku prostokątnej wstęgi w.cz. przy wzmocnieniu |Ao|2, dla którego splot występujący we wzorach (1) i (2) można wykonać ściśle. Jeżeli ponadto ΔfHF << fo, gdzie fo jest dolną częstością pasma po dodatniej stronie widma, to można pokazać, że całkę omawianego splotu lepiej niż
|
przybliża (K i t t e l 1978):
| (6) |
Dla wstęgi o szerokości rzędu 100 kHz i stałej czasowej wygładzającego filtru RC rzędu 1 s, użycie wyrażenia (6) w miejsce dotychczasowego przybliżenia czyni różnicę 0,01% w ocenie <v2> występującego we wzorze (2). Jest to, oczywiście, zaniedbywalna różnica.
Często rolę filtru wygładzającego spełniają obwody całkujące typu RC, których charakterystyka przenoszenia wyraża się wzorem:
| (7) |
Szereg niezależnych filtrów tego typu ma charakterystykę będącą iloczynem charakterystyk filtrów składowych. Równoważna stała czasowa (stosowalna w (5)) filtru RC, zgodnie z przyjętą tutaj definicją, wyraża się przez:
| (8) |
Wypada zwrócić uwagę na fakt, że wielkość RC, zwana stałą czasową filtru, jest tutaj aż 4-krotnie mniejsza niż równoważna stała czasowa stosowana do obliczania czułości systemu odbiorczego. Z uwagi na podobieństwo nazw i oznaczeń tych dwóch wielkości nie jest trudno o pomyłkę.
Analogicznie jak w przypadku filtru pojedynczego, równie łatwo obliczyć równoważne stałe czasowe filtru złożonego z dwóch niezależnych od siebie obwodów RC (R1C1 i R2C2):
| (9) |
Równoważne szerokości charakterystyk innych filtrów m.cz. można znaleźć np. u B r a c e w e l l a (1962) lub T i u r i e g o (1964), ale trzeba je podwajać przy użyciu we wzorze (5), ze względu na inną definicję ΔfLF lub τ stosowaną w tych źródłach. W tychże źródłach podano także równoważne szerokości pasm filtrów w.cz. (por. też E s e p k i n a i in. 1973; P r i c e 1976; B r a c e w e l l 1965).
Rzetelność każe wspomnieć o pewnej trudności pogodzenia teorii z doświadczeniem, z którą zetknąłem się w praktyce. Otóż zaobserwowałem, że użycie dwóch jednakowych filtrów RC na wyjściu odbiornika polepszało czułość systemu (rozumianą jako szerokość ścieżki szumowej zapisu) znacząco więcej niż użycie pojedynczego filtru o dwukrotnie większej stałej czasowej. Ze wzoru (9) wynika, że nie powinno być żadnej różnicy w czułości systemu w tych dwóch sytuacjach. Kierując się sugestią K i t t e l a (1978), uwzględniłem lepsze przybliżenie oceny czułości korzystając ze wzoru (6) i stwierdziłem nieznaczny wpływ tego czynnika. Z braku innych argumentów trzeba przystać na wyjaśnienie (także zasugerowane przez K i t t e l a), które przypisuje filtrowi tandemowemu (podwójnemu) lepsze usuwanie przydźwięku sieci (50 Hz, szum niegaussowski).
Istnieje wiele dogłębnych opracowań teorii detekcji sygnałów deterministycznych zakłóconych szumami normalnymi, jak też detekcji samych szumów (np. L e v i n 1974; S i f o r o v 1974; K n o c h i E k i e r t 1979). Znakomita ich większość została opracowana dla celów radiotechniki, ale metody opisu przetwarzania sygnałów tak ugruntowane znalazły swe zastosowanie również w wielu pracach z dziedziny radioastronomii, szczególnie te dotyczące sygnałów losowych (B e n d a t 1958; E s e p k i n a i in. 1973).
Do wielu celów w radioastronomii nie jest konieczne wprowadzanie tak złożonego aparatu matematycznego, jak we wspomnianych pracach. Tutaj, z bardzo dobrym przybliżeniem niemal wszystkie sygnały można traktować jako szumy gaussowskie i wówczas, przy odpowiednim podejściu, wiele opisów znacznie się upraszcza. Niech poniższa prosta analiza posłuży za poparcie tej opinii.
Znanym faktem jest, iż sygnał wejściowy detektora jest szumem wąskopasmowym o rozkładzie chwilowych amplitud (obwiedni R) typu Rayleigha:
| (10) |
Uzasadnienie istnienia takiego rozkładu uzyskuje się przez konstrukcję sygnału analitycznego (np. K n o c h i E k i e r t 1979; S w i e s z n i k o w 1965).
Detektor jest zawsze urządzeniem nieliniowym i zwykle jego działanie opisują złażone funkcje. Dla wielu potrzeb stosowane są detektory o charakterystyce potęgowej (np. liniowe lub kwadratowe), których działanie można opisać równaniem:
| (11) |
gdzie V jest proporcjonalne do napięcia wyjściowego detektora. Bez utraty ogólności przyjmę dalej, że jest to wprost napięcie wyjściowe.
Rozkład prawdopodobieństwa amplitud sygnału V można łatwo obliczyć opierając się na fakcie, że prawdopodobieństwo znalezienia napięcia V między V i V + dV jest takie same, jak znalezienia obwiedni R pomiędzy R i R + dR. Nieskomplikowane operacje na wzorach (10) i (11) prowadzą do rozkładu:
| (12) |
lub, wyrażając to samo przez obwiednię sygnału wejściowego, do:
| (13) |
Wartość średnią napięcia wyjściowego detektora można, teraz już prosto, wyliczyć ze wzoru (12) lub (13):
| (14) |
gdzie Γ jest funkcją gamma Eulera. Z teorii tej funkcji (np. K o t l a r s k i 1971; D w i g h t 1961 czy B r a n d t 1976) wiadomo, że w ogólności dla x > 0, Γ(x) > 0 i w szczególności:
|
|
W przypadku detektora liniowego (n = l) jest więc:
|
|
Te dwa wyniki są dobrze spopularyzowane.
Ze wzoru (14) wynika, że znajomość charakterystyki detektora (znajomość parametru n) pozwala na pomiar mocy szumów wejściowych poprzez pomiar średniego napięcia wyjściowego detektora (stałą proporcjonalności, która tutaj nie występuje, wyznacza się przez kalibrację bezwzględną).
Powyższą dyskusję nietrudno uogólnić na bardziej złożone charakterystyki detektorów (f(R)), o ile można je rozwinąć na szereg potęgowy:
| (15) |
Prawdopodobieństwo, że sygnał wyjściowy detektora potęgowego przekroczy m-krotnie wartość średnią, wynosi:
| (16) |
Skorzystanie z rozkładu (12) i wartości średniej (14) prowadzi wprost do:
| (17) |
skąd w szczególności:
| (17a) |
Wzory (17) i (17a) pozwalają ocenić, ile razy średnie napięcie wyjściowe detektora powinno być mniejsze od napięcia zasilania (lub innego poziomu granicznego, którego sygnał detektora nie powinien przekraczać), aby prawdopodobieństwo jego przekroczenia nie przewyższało zadanej wartości. Na przykład dopuszczając prawdopodobieństwo 0,001, średnie napięcie wyjściowe detektora liniowego trzeba ustalić nie wyżej niż na poziomie ok. 1/3 napięcia zasilania, a w przypadku detektora kwadratowego — 1/7 napięcia zasilania.
Odbiornik przełączany, znany też pod nazwą modulacyjnego lub odbiornika Dicke'ego, jest jednym z najszerzej stosowanych w radioastronomii od czasu wynalezienia w połowie lat 40. (D i c k e 1946; por. też R o b i n s o n 1964; K r a u s 1966; P r i c e 1976). Sukces tego urządzenia bierze się głównie z jego prostoty i możliwości redukcji błędu wynikającego z własnych fluktuacji wzmocnienia sekcji w.cz. odbiornika. Te wolnozmienne fluktuacje mają widmo odwrotnie proporcjonalne do częstości i w związku z tym są szeroko znane pod nazwą szumów typu 1/f (niekiedy są zwane tez szumem migotania – flicker noise). Warto wspomnieć, że chociaż wiadomo już bardzo dużo na temat tego szumu, to ciągle cieszy się on dużym zainteresowaniem z powodu niejasnego wciąż pochodzenia (np. W o l f 1978).
Działanie odbiornika Dicke'ego opiera się na pomiarze małej różnicy mocy sygnałów zamiast całego, często nieporównalnie większego, sygnału wejściowego. W tym celu na wejście odbiornika doprowadza się na przemian sygnał z anteny (TA) i sygnał ze źródła szumów o znanej temperaturze szumowej (Tr). Głębokość modulacji wynikającej z przełączania jest proporcjonalna do różnicy temperatur TA – Tr. Jeżeli odbiornik ma detektor kwadratowy, na wyjściu mierzy się różnicę mocy wejściowych jako różnicę w napięciach, za pomocą detektora synchronicznego (zwanego też fazowym lub koincydencyjnym). Ponieważ szum typu 1/f na częstościach powyżej kilkudziesięciu herców jest wielokrotnie słabszy (w sensie mocy widmowej) niż w okolicy 1 Hz, zatem przy częstościach przełączania rzędu 100 Hz lub większych można spodziewać się znacznej redukcji wpływu wolniejszych fluktuacji (na tyle wolnych, aby można było zaniedbać zmiany wzmocnienia na jednym cyklu przełączania wejścia odbiornika) na wynik pomiaru.
Nie jest trudno zauważyć, że zmiana wzmocnienia Δ|A|2 spowoduje na wyjściu odbiornika przełączanego z detektorem kwadratowym względny błąd pomiaru ΔT/(TA + Tr) równy:
|
Oznacza to, że wielce korzystna cecha niwelacji fluktuacji wzmocnienia odbiornika przełączanego znika ze wzrostem różnicy TA – Tr. Przy różnicy równej połowie temperatury systemowej (TA) fluktuacje są już tylko trzykrotnie mniejsze niż w odbiorniku bez przełączania. W przypadku sygnałów znacznie przewyższających poziomem mocy moc źródła porównawczego podstawowa własność odbiornika przełączanego jest niemal dokładnie stracona. Sytuacja taka pojawia się szczególnie ostro w wąskopasmowych obserwacjach Słońca na mniejszych częstościach (fale metrowe i dłuższe), gdzie ma się do czynienia z sygnałami przewyższającymi promieniowanie Słońca spokojnego nawet o 60 dB (milion razy). Chociaż istnieją inne rozwiązania systemów odbiorczych, pozwalające mierzyć sygnały o dynamice tego rzędu z zadowalającą dokładnością, to jednak spotyka się zwykłe odbiorniki przełączane w służbach Słońca tego zakresu fal (C o f f e y i S h e a 1977); m. in. w toruńskiej służbie na częstości 127 MHz taki odbiornik był w użyciu przez ostatnie kilkanaście lat.
Dla polepszenia stabilności wzmocnienia i zwiększenia dynamiki odbiornika, w stopnie w.cz. (często p.cz.) wprowadza się automatyczną regulację wzmocnienia (zwaną dalej ARW). W wyniku tego zabiegu uzyskuje się prawie liniową (w mocy) charakterystykę wzmocnienia dla sygnałów małych i zakrzywioną dla większych. W takim układzie pojawia się jednak problem kalibracji (wyznaczania rzeczywistej charakterystyki) odbiornika. Problem ten wymaga skalibrowanych generatorów szumów o wyjątkowo dużej mocy widmowej. Ten wymóg w praktyce rzadko jest zaspokajany. Prowadzi to do dalekiej ekstrapolacji charakterystyki wyznaczonej na jej początkowym odcinku (dla małych sygnałów), a konsekwencją tego są ogromne błędy w ocenie dużych sygnałów. Co więcej, dostępna literatura nie podaje teoretycznych charakterystyk odbiorników przełączanych z ARW w zastosowaniu do pomiaru sygnałów szumowych. Nie bardzo było zatem wiadomo, jak należy ekstrapolować (lub nawet interpolować) zmierzoną w pewnym obszarze charakterystykę. U B e n d a t a (1958) oraz L a w s o n a i U h l e n b e c k a (1950) są wprawdzie podane pewne rozważania na temat parametrów statystycznych sygnałów wyjściowych odbiornika z ARW, jednakże nie są one istotne przy rozpatrywaniu charakterystyki odbiornika jako całości.
Proponowana niżej dyskusja teoretycznej charakterystyki odbiornika przełączanego z ARW pozwoli związać sygnały wyjściowe z wejściowymi, poprzez parametry odbiornika, za pomocą prostych wzorów. Na tej podstawie można będzie wnioskować, iż jeżeli już trzeba używać odbiornika przełączanego do obserwacji Słońca, to powinien on zawierać raczej detektor liniowy niż kwadratowy, z powodu większej dynamiki tego pierwszego. Dalszym rezultatem dyskusji będzie propozycja prostej i obiecującej metody kalibracji odbiornika i systemu odbiorczego z istotnym, jak podpowiada praktyka, zastrzeżeniem o idealności przełącznika wejściowego i detektora potęgowego.
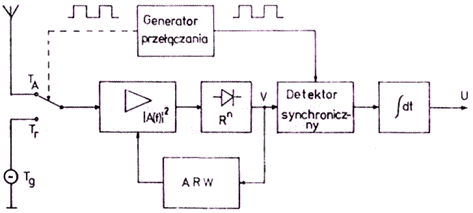 |
| Rys. 1. Odbiornik przełączany z automatyczną regulacją wzmocnienia (ARW) |
Rozważania ograniczę do wersji odbiornika przedstawionego na rys. l,
składającego się z liniowej sekcji wzmocnienia w.cz. z regulowanym
wzmocnieniem |A|2, detektora obwiedni o charakterystyce Rn,
detektora synchronicznego sterowanego sygnałem prostokątnym wytwarzanym
w generatorze przełączania i futru m.cz. (integratora). Generator
przełączania steruje również przełącznikiem wejściowym (przełącznik
diodowy), który doprowadza do odbiornika sygnał antenowy (TA) lub
źródła porównawczego (Tr). Wzmocnienie w pętli ARW można dobrać tak,
by średni (po czasie obejmującym przynajmniej kilka okresów przełączania)
sygnał detektora obwiedni można było uważać za stały w czasie.
Wcześniej pokazałem, że średnie napięcie wyjściowe potęgowego detektora obwiedni jest proporcjonalne do średniego kwadratu chwilowej amplitudy sygnału wejściowego w potędze n/2, gdzie n opisuje charakterystykę detektora, a zatem, zgodnie z twierdzeniem Nyquista i wzorem (14), także do Tn/2, gdzie T jest równoważną temperaturą szumową (stacjonarnego) sygnału na wejściu odbiornika. Jeżeli przełączanie sygnałów wejściowych będzie dostatecznie wolne na tyle, by uzyskany w rezultacie przełączania wycinek sygnału wejściowego można było uważać za reprezentatywny dla realizacji (jeśli warunku tego nie uda się spełnić, to w dalszym ciągu należy rozumieć, że fragment ten traktuję jako średnią po przestrzeni wielu realizacji procesu ergodycznego) i jednocześnie na tyle szybkie, by układ ARW już nie „widział" przełączania, to w każdej pozycji (stanie) przełącznika wejściowego na wyjściu detektora obwiedni pojawia się napięcie proporcjonalne do wzmocnienia odbiornika takie, że:
| (18) |
Układ ARW z założenia zapewnia, że z dobrym przybliżeniem suma napięć średnich ze wzorów (18) utrzymywana jest na stałym poziomie, co oznacza, że:
| (19) |
Detektor synchroniczny, umieszczony za detektorem obwiedni, odwraca polaryzację (zmienia znak) napięcia wejściowego w takt sygnału przełączania, co po uśrednieniu (w integratorze) jest równoważne odjęciu prawych stron wyrażeń (18). W praktyce często na detektor synchroniczny podaje się sygnał zmniejszony o wartość średnią, ale dla tej analizy jest to nieistotne. Uwzględniając jeszcze proporcjonalność (19), na wyjściu odbiornika dostaje się ostatecznie napięcie (prąd) proporcjonalne do:
| (20) |
gdzie Umax jest pewną stałą proporcjonalności. Wyrażenie (20) można uczynić bardziej przejrzystym przez położenie za jednostkę temperatury temperaturę źródła porównawczego Tr, a za jednostkę napięcia wartość Umax. Wtedy:
| (21) |
Nietrudno zauważyć, że U jest ograniczone do przedziału (–1,1) lub (–Umax,Umax), co się sprawdza przez przejścia graniczne z TA do nieskończoności. Fakt ten uzasadnia nazwę współczynnika proporcjonalności we wzorze (20). Proste przekształcenie wzoru (21) prowadzi do wyrażenia pozwalającego obliczać TA przy danym U:
| (22) |
albo, używając jednostek bezwzględnych:
| (23) |
Równania od (20) do (23) opisują tę samą charakterystykę odbiornika i stanowią bodajże najważniejszy punkt rozważań. Określają one związek sygnału (napięcia) wyjściowego odbiornika przełączanego z ARW, z równoważną temperaturą szumową sygnału wejściowego. Należy podkreślić, że ani TA, ani Tr nie są „czystymi" sygnałami, przypisanymi tutaj antenie i źródłu porównawczemu. Jak wynika z przyjętych założeń, są to sygnały, które odbiornik efektywnie „widzi" na wejściu, a zatem zawierają one w sobie również temperaturę szumową odbiornika (Tr) i są zmniejszone o straty na przełączniku i wskutek ewentualnego niedopasowania anteny (łącznie z liniami przesyłowymi) i źródła porównawczego do impedencji wejściowej odbiornika. Z tego powodu nie należy się spodziewać, by napięcie wyjściowe odbiornika osiągało wartość –Umax; TA zawsze jest większe od zera (w najlepszym przypadku są to szumy własne odbiornika). Jeśli jednak TA będzie zaniedbywalnie małe w porównaniu z Tr, to napięcie U można będzie uważać za dowolnie bliskie –Umax. Taka sytuacja wynikłaby, gdyby w miejscu sygnału porównawczego podać sygnał o bardzo dużej mocy (np. z intencją wyznaczenia Umax = |–Umax|).
Ze wzoru (21) łatwo jest wyliczyć, że na to, by napięcie. wyjściowe osiągnęło poziom równy 99% wartości maksymalnej potrzeba sygnału wejściowego zaledwie ok. 200 razy przewyższającego moc dostarczaną ze źródła porównawczego w przypadku detekcji kwadratowej, zaś ok. 4000 razy przy detekcji liniowej. Liczby te mogą być miarą dynamiki obu odbiorników. Tak np. na częstości rzędu 100 MHz, gdzie wygodne źródło porównania przy obserwacjach słabych źródeł powinno mieć moc odpowiadającą w przybliżeniu temperaturze otoczenia (taka jest temperatura równoważna tła galaktycznego), co przy szerokich charakterystykach promieniowania anten będzie odpowiadać mocy ok. dwu- trzykrotnie większej od odbieranej ze spokojnego Słońca, powyższe liczby odpowiadają granicom ok. 500 (27 dB) i 10000 razy (40 dB) przewyższającym promieniowanie spokojnego Słońca dla przypadków (odpowiednio) odbiornika z detektorem kwadratowym i liniowym. Takie dynamiki, zwłaszcza ta w przypadku detektora kwadratowego, są niewystarczające dla służb Słońca w tym zakresie częstości. W praktyce nie osiąga się nawet wspomnianych wyżej granic dynamiki ze względu na niedoskonałości przełącznika wejściowego i detektora potęgowego, o czym będzie jeszcze mowa.
Przebieg charakterystyki odbiornika przełączanego z ARW opisanej wzorami (20)–(23) podpowiada sposób kalibracji systemu odbiorczego. Aby można było określać moc sygnału wejściowego za pomocą pomiaru napięcia na wyjściu odbiornika (korzystając np. ze wzoru (23) trzeba znać, oprócz charakterystyki detektora czyli tutaj parametru n, graniczne napięcie wyjściowe i równoważną temperaturę sygnału porównawczego.
W celu określenia parametru Umax trzeba wyznaczyć najpierw poziom zerowy, od którego mierzy się U. Jest na to niemal idealny sposób: zatrzymanie przełącznika wejściowego w jednej z dwóch pozycji, brak modulacji bowiem oznacza na wyjściu odbiornika tyle samo, co zrównanie mocy TA i Tr,. Do wyznaczenia napięcia granicznego Umax potrzeba teraz jedynie generatora (niekoniecznie skalibrowanego) sygnału szumowego o bardzo dużej mocy włączonego bądź na miejsce anteny, bądź źródła porównawczego (w tym przypadku na wyjściu pojawi się napięcie –Umax). Jeżeli doprowadzona w ten sposób moc będzie dostatecznie duża, to także wyjściowy sygnał będzie dowolnie bliski granicznemu. Ze względu na silne zakrzywienie charakterystyki odbiornika, wymagania na stabilność, a nawet powtarzalność doprowadzanego sygnału są niewielkie. Taki generator szumu jest stosunkowo łatwo osiągalny, gdyż diody Zenera w pewnych układach mogą generować szumy o mocach ponad 50 dB wyższych od temperatury otoczenia (B o b n' e v 1971). Moc sygnału porównawczego jest tutaj tylko współczynnikiem proporcjonalności dla skali temperatur lub mierzonego strumienia. Jego wyznaczenie wiąże się z nawiązaniem do bezwzględnej skali strumienia, które wykonuje się przez obserwację radioźródeł o znanych strumieniach promieniowania.
Chciałbym podkreślić, że powyższa kalibracja odbiornika i całego systemu odbiorczego nie wymaga skalibrowanych i stabilnych generatorów szumów (wyjąwszy oczywiście źródło porównawcze, które powinno być jak najbardziej stabilne), co oznacza wyeliminowanie dodatkowego, poważnego źródła błędów w postaci niepewnych generatorów i nie zawsze zgodnych impedancji. Łatwo też całą procedurę kalibracji odbiornika zautomatyzować gwoli poprawienia dokładności wyników pomiarów.
Dotychczasowa dyskusja była prowadzona przy milczącym założeniu, że wejście antenowe jest doskonale odizolowane od źródła porównawczego — i na odwrót. W praktyce warunek ten nigdy nie jest spełniony. W poniższej analizie pokażę, że nawet niewielkie przenikanie sygnałów pomiędzy wejściami obniża znacząco dynamikę odbiornika przełączanego z ARW i detektorem liniowym.
Jeżeli istnieje różnica mocy sygnałów TA i Tr, na wejście, na które jest doprowadzony słabszy sygnał dostaje się część tej różnicy. Niech ową część określa współczynnik α, przyjmujący wartości z przedziału [0,1] i reprezentujący niedoskonałość izolacji wejść. Dla ustalenia uwagi przyjmę, że sygnał antenowy TA jest większy. Wobec tego rzeczywista wartość sygnału porównawczego wyniesie:
| (24) |
gdzie T'r jest wielkością niezależną od TA i równą Tr tylko wtedy, gdy TA = T'r. Zauważam najpierw, iż z nowego określenia Tr wynika, że:
|
a zatem także (ze wzoru (20)):
|
co już sugeruje, chociaż nie dowodzi, zmniejszenie dynamiki. Aby pokazać, że nie jest to tylko zawężenie skali sygnału wyjściowego, trzeba wyrazić napięcie wyjściowe w jednostkach napięcia granicznego. Niech zatem:
| (25) |
Proste przekształcenie wzoru (23) z uwzględnieniem (24) prowadzi do związku:
| (26) |
który po uwzględnieniu zależności (25) przechodzi w:
| (27) |
Wzór (27) pozwala obliczyć jakiego potrzeba sygnału antenowego TA, aby sygnał wyjściowy osiągnął zadany poziom U. Warto zauważyć, że gdy α = 0, wzór ten staje się identyczny ze wzorem (23).
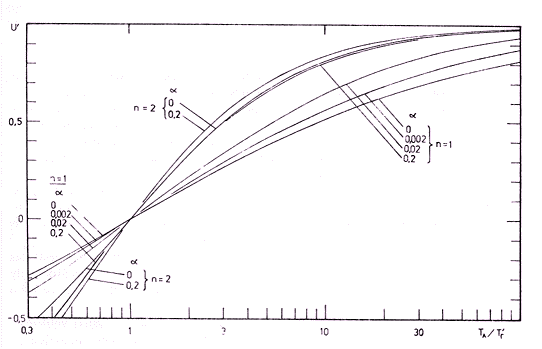 |
| Rys. 2. Charakterystyki wzmocnienia odbiornika przełączanego z ARW z różnymi detektorami (n = 1 dla detektora liniowego, n = 2 dla kwadratowego) i różnymi izolacjami wejścia antenowego od porównawczego (α) |
Na rys. 2 przedstawiłem kilka znormalizowanych charakterystyk odbiornika
przełączanego z ARW, sporządzonych na podstawie wzoru (27), dla przypadków
detektora liniowego i kwadratowego. Zwraca uwagę szybkie zmierzanie
charakterystyki odbiornika z detektorem liniowym do przebiegu wyznaczonego
przez charakterystykę odbiornika z detektorem kwadratowym ze wzrostem
wartości α, co oznacza także podobną degradację
dynamiki.
Na to, by napięcie wyjściowe osiągnęło 99% wartości granicznej (U' = 0,99) w obecności detektora liniowego i przy α = 0,02 (izolacja 17 dB), potrzeba sygnału TA = 692·T'r, co jest aż 57 razy (ponad 17 dB) mniej niż w przypadku, gdy α = 0. Podobny rachunek wykazuje, że nawet przy izolacji wejść rzędu 30 dB (α = 0,001) odbiornik ten traci na dynamice ok. pięciokrotnie (7 dB) w stosunku do przypadku doskonałego przełącznika wejściowego.
Izolacja 17 dB w obecności detektora kwadratowego powoduje zmniejszenie dynamiki odbiornika w punkcie U' = 0,99 o zaledwie 0,1 dB.
W charakterze detektorów obwiedni stosuje się powszechnie diody półprzewodnikowe. W zakresie niewielkich napięć charakterystyki diod opisuje dobrze tzw. równanie diody (np. R o t k i e w i c z i in.1973; S e e l y 1968), z którego wynika, że prąd diody jest proporcjonalny do:
| (28) |
gdzie e jest ładunkiem elektronu, V — doprowadzonym napięciem, m stałą zależną od materiału półprzewodnika (dla germanu m = 1, dla krzemu m = 2), k stałą Boltzmanna, a T — temperaturą bezwzględną złącza. Przy dużych napięciach dodatnich, zazwyczaj większych od 1 V, przebieg charakterystyki diody zbliża się do prostoliniowego, natomiast dla napięć ujemnych od pewnego punktu występuje gwałtowny wzrost prądu wstecznego. Do podstawowych wad diod jako detektorów trzeba zaliczyć zależności ich parametrów od temperatury otoczenia i istnienie pewnego prądu wstecznego.
Wspomniane zakrzywienie charakterystyki dla małych sygnałów może być dobrze przybliżone przez parabolę. Z tego powodu w praktyce obszar ów wykorzystuje się przy projektowaniu detektorów kwadratowych. Obranie punktu pracy diody w zakresie liniowym jej charakterystyki daje przybliżenie, na ogół dobre, detektora liniowego.
Ważną rzeczą jest zwrócenie uwagi na skutki użycia półprzewodnikowego detektora liniowego w odbiorniku przełączanym z ARW. Otóż w przypadku małych sygnałów (gdy TA ≈ Tr) będzie on dobrze przybliżał idealny detektor liniowy. Jednak dla sygnałów już o kilka decybeli wyższych sytuacja bardzo się komplikuje.
Oto uzasadnienie ostatniego zdania. W rozdz. 3 pokazałem, że średni sygnał wyjściowy detektora liniowego nie powinien przekraczać poziomu rzędu 1/3 napięcia granicznego (jeśli po detektorze nie ma pasywnego filtru pasmowego, to tą granicą jest co najwyżej napięcie zasilania), co oznacza, że w przypadku napięcia zasilania 15 V ten średni poziom powinien wynosić ok. 5 V. W odbiorniku przełączanym, dla dużych TA poziom średni odpowiadający sygnałowi TA jest ok. 2 razy wyższy niż średni poziom wyjściowy detektora, co czyni, że ten ostatni powinien mieć wartość niewiele większą niż 2 V. Jest to zaledwie ok. dwukrotnie wyżej niż początek obszaru liniowości przeciętnej diody. W konsekwencji, już przy sygnałach TA ≈ 4Tr, sygnał ze źródła porównawczego przez większość czasu podlega detekcji w nieliniowym obszarze charakterystyki diody, gdy tymczasem sygnał antenowy podlega praktycznie tylko detekcji liniowej. Wtedy też, oczywiście, tracą sens zależności (20)–(23). Łatwo zauważyć, że rzeczywista charakterystyka takiego odbiornika mieści się gdzieś pomiędzy charakterystykami odbiorników z idealnym detektorem liniowym i idealnym detektorem kwadratowym. W związku z tym dynamika tego odbiornika jest także znacząco mniejsza niż odbiornika z idealnym detektorem liniowym.
Innym ograniczeniem dynamiki odbiorników przełączanych z detektorami półprzewodnikowymi jest zachowanie się rzeczywistej diody w przypadku napięć ujemnych. Z przebiegu charakterystyki diody widać, że w przypadku małych napięć szumowych (rzędu 0,1 V lub mniej) detekcja w ogóle nie zachodzi lub jest bardzo nieskuteczna. Skutkiem tego zjawiska jest szybsze zmierzanie charakterystyki rzeczywistej odbiornika do wartości maksymalnej Umax niżby to wynikało z charakterystyk teoretycznych typu (20).
Proste wzory opisujące charakterystykę wzmocnienia odbiornika przełączanego dotąd przedstawione uzyskałem głównie dzięki załozeniu, że wzmocnienie w pętli ARW jest na tyle duże, by można było zaniedbywać zmiany średniego napięcia wyjściowego detektora
|
Niech, jak to często bywa w rzeczywistości, wzmocnienie w paśmie
przenoszenia wzmacniacza w.cz. opisuje proporcjonalność:
|
|
oraz (z powyższego i ze sposobu zdefiniowania |A|2):
|
gdzie Vo jest pewną stałą, to także:
|
Zaniedbanie teraz jedynie zmian wielkości
|
|
Zwykłe odbiorniki przełączane, w rodzaju odbiornika opisanego w poprzednim punkcie, tracą swój podstawowy walor redukcji niestabilności wzmocnienia ze wzrostem różnicy mocy wejściowych TA – Tr. Pokazałem ponadto, że poważne problemy wynikają z faktów niedoskonałości przełącznika wejściowego i potęgowych detektorów obwiedni. Odbiornik, który byłby wolny od tych wad, powinien pracować w stanie stałego zrównoważenia obu sygnałów wejściowych. Takie urządzenie zostało opracowane przez R y l e'a i V o n b e r g a (1948; M a c h i n i in. 1952). W oryginalnym rozwiązaniu źródło sygnału porównawczego było sterowane tak, aby sygnał na wyjściu zwykłego odbiornika przełączanego był zawsze zerem. Moc szumów generowanych przez diodę próżniową, użytą w charakterze źródła porównawczego, jest proporcjonalna do jej prądu anodowego. Pomiar tego prądu daje zatem miarę mocy dostarczanej przez antenę.
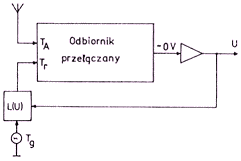 |
| Rys. 3. Odbiornik Ryle'a-Vonberga |
Jeżeli tłumik ma charakterystykę L(U), gdzie U jest napięciem sterującym tłumika i jednocześnie napięciem wyjściowym odbiornika, to z warunku zrównoważenia sygnałów wejściowych TA = Tr jest:
| (29) |
gdzie To jest temperaturą otoczenia (temperatura fizyczna tłumika), a Tg — temperaturą równoważną szumów wytwarzanych w generatorze. Znajomość charakterystyki L pozwala mierzyć sygnał antenowy przez pomiar napięcia wyjściowego U i skorzystanie ze wzoru (29). W przypadku, gdy jest ona eksponencjalna, tzn. L ~ 10U:
| (30) |
gdzie a i b są pewnymi stałymi. Wzór (30) oznacza, że napięcie wyjściowe odbiornika jest proporcjonalne do logarytmu mocy sygnału wejściowego. Przykład praktycznej realizacji odbiornika przełączanego z ARW podano u B o r k o w s k i e g o i in. (1975), dlatego tutaj ograniczę się tylko do omówienia przykładowych rozwiązań podzespołów różniących odbiornik Ryle'a-Vonberga od tamtego.
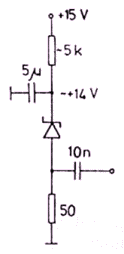 |
| Rys. 4. Generator szumów oparty na diodzie Zenera |
Niewątpliwie najważniejszym i najbardziej krytycznym elementem odbiornika Ryle'a-Vonberga jest tłumik. Jego charakterystyka i zakres tłumienia przenoszą się na charakterystykę i dynamikę odbiornika jako całości. Logarytmiczna charakterystyka systemu odbiorczego (typu (30)) zapewnia nie tylko dużą dynamikę, ale takie w przybliżeniu ten sam błąd względny przy pomiarach sygnałów dużych i małych, dlatego też najbardziej wskazaną charakterystyką tłumika jest funkcja eksponencjalna.
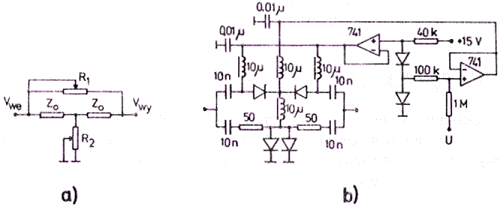 |
| Rys. 5. Regulowany tłumik typu T: a) idea, b) przykład rozwiązania opartego na diodach PIN |
Charakterystykę eksponencjalną zapewnia tłumik typu T (rys. 5a),
który charakteryzuje się niezależnością impedancji wejściowej
i wyjściowej od współczynnika tłumienia
(L = (Vwy/Vwe)2 ≤ 1)
pod warunkiem obciążenia z obu
stron impedancją charakterystyczną Zo oraz stałości iloczynu
rezystancji R1R2 (J o h n s o n 1950). Ten ostatni warunek wydaje
się trudny do praktycznego zrealizowania. Okazuje się jednak, że
stałość tego iloczynu można stosunkowo dobrze utrzymać, wykorzystując
pewne własności diod PIN. Opierając się na zrealizowanym przez
V i l e s a (1977) rozwiązaniu tłumika regulowanego typu L,
opracowałem wersję typu T, którą przedstawia rys. 5b. Diody PIN
są tutaj podwojone w celu powiększenia zakresu tłumienia
(do 60 dB). Trzeba dodać, że idea tego tłumika wymaga użycia
diod o bardzo zbliżonych parametrach. Para diod poza układem samego
tłumika służy także do kompensacji temperaturowej całego urządzenia.
Wszystkie idee przedstawione w tej pracy zrodziły się (niebezboleśnie) z praktycznych potrzeb toruńskich obserwacji Słońca na częstości 127 MHz. Najwięcej kłopotów dostarczało zagadnienie pomiaru dużych sygnałów — problem kalibracji odbiornika. Oczywiście, nie pomagało w tym obiegowe przekonanie, że charakterystyka odbiornika przełączanego z ARW powinna być bliska logarytmicznej, bo pomiary, przynajmniej w przypadku większych sygnałów, wyraźnie temu przeczyły.
Skutkiem wspomnianej niezgodności były rozbieżności toruńskich wyników obserwacji Słońca i wyników uzyskanych w innych stacjach (chodzi tu głównie o różnice w pomiarach dużych strumieni). Z przedstawionego w tej pracy opisu zachowania się odbiornika przełączanego wynika, że na krzywiznę charakterystyki wzmocnienia, a zatem również na dynamikę całego systemu odbiorczego, przemożny wpływ ma rodzaj detektora obwiedni, jego charakterystyka (w sensie odstępstwa od potęgowej), izolacja wejścia antenowego od źródła sygnału porównawczego i wartość wzmocnienia w pętli ARW. Wnioski te znajdują także zadowalające poparcie doświadczalne (przygotowuję odpowiednie materiały do publikacji na tych łamach).
Niejako ubocznym produktem przeprowadzonej tu analizy jest uzasadnienie marzenia o obiecująco prostym sposobie kalibracji zwykłego odbiornika przełączanego, pod warunkiem, że postęp techniki elektronicznej uczyni łatwo dostępnymi detektory, które będą bliższe idealnym niż zwykłe diody półprzewodnikowe. Taki odbiornik, ze względu na prostotę konstrukcji, byłby względnie łatwo osiągalny dla zaawansowanych radioamatorów. Łatwość kalibracji (bez potrzeby używania skalibrowanych generatorów szumów) i niepoślednia dynamika uczyniłyby możliwym rozwój pożytecznego wówczas ruchu amatorskiego w tej dziedzinie. Trzeba wszakże pamiętać, że nawet tak udoskonalony odbiornik przełączany nie spełnia wymagań współczesnej profesjonalnej służby Słońca na falach metrowych. Sporą przewagę w tym względzie nad przełączanym ma odbiornik Ryle'a-Vonberga.
B e n d a t, J. S., 1958, Principles and Application of Random Noise Theory, J. Wiley and Sons, N. Y.
B o b n e v, M. P ., 1971, Generirovanie sluchajnykh signalov, Ehnergiya, M.
B o r k o w s k i, K., G o r g o l e w s k i, S., U s o w i c z, J., 1975, Post. Astr., 23, 141.
B r a c e w e l l, R. N., 1962, w: Handbuch der Physik, 54, 42 (Springer-Verlag, Berlin).
B r a c e w e l l, R. N., 1965, The Fourier Transform and Its Applications, McGraw-Hill, N. Y.
B r a n d t, S., 1976, Statiatical and Computational Methods in Data Analysis, North-Holland, Amsterdam.
C h r i s t i a n s e n, W. N., H ö g b o m, J. A., 1969, Radiotelescopes, Cambridge University Press. Cambridge.
C o f f e y, H. E., S h e a, M. A., (wyd.), 1977, Directory of Solar-Terrestrial Physics Monitoring Stations, SCOSTEP, AFGL, WDC-A, Boulder, Colo.
D i c k e, R. H., 1946, Rev. Sci. Intrum., 17, 265.
D w i g h t, H. B., 1961, Tables of Integrals and Other Mathematical Data, McMillan, N. Y.
E s e p k i n a, N. A., K o r o l' k o v, D. W., P a r i j s k i j, Yu. N., 1973, Radioteleskopy i radiometry, Nauka, M.
E v a n s, J. V., 1968, w: Radar Astronomy, 516 (wyd. E v a n s, J. V., H a g f o r s, T., McGraw-Hill,N. Y.).
F a r b e r, 0., 1969, Radio, Nr 1, 37.
J o h n s o n, W. C., 1950, Transmission Lines and Networks, McGraw-Hill, N. Y.
K i s l j a k o v, A. G., 1978, Radiofizika, 21, 448.
K i s l j a k o v, A. G., 1979, tamże, 22, 513.
K i t t e l, P., 1977, Rev. Sci. Instrum., 48, 1214.
K i t t e l, P., 1978, informacja osobista.
K n o c h, L., E k i e r t, T., 1979, Modulacja i detekcja, WKŁ, Warszawa.
K o r o l' k o v, D. V., 1979, Radiofizika, 22, 511.
K o t l a r s k i, I., 1971, w zbiorze: Matematyka – Poradnik inżyniera, WNT, Warszawa.
K r a u s, J. D., 1966, Radio Astronomy, McGraw-Hill, N. Y.
L a w s o n, J. I., U h l e n b e c k, G. E., 1950, Threshold Signals, MIT Radiation Laboratory Series, 24, McGraw-HilI, N. Y.
L e v i n, B. R., 1974, Teoreticheskie osnovy statisticheskoj radiotekhniki, Sov. radio, M.
M a c h i n, K. E., R y l e, M., V o n b e r g, D. D., 1952, Proc. IEE, 99, 127.
N i k o l a e v, A. G., 1964, Radioteplolokacya, Sov. radio, M.
P e p p e r, M. G., 1975, Ph. D. Thesis, University of Kent.
P e p p e r, M. G., B r o w n, J. B., 1979, J. Phys. E: Sci. Instr., 12, 31.
P r i c e, R. M., 1976, Meth. Exp. Phys., 12B, 201.
R i c e, S. 0., 1944, Bell Sys. Tech. J., 23, 282.
R o b i n s o n, B. J., 1964, Ann. Rev. Astron. Astrophys., 2, 401.
R o t k i e w i c z, W., R o t k i e w i c z, P ., Z a l e s k i, B., 1973, Technika odbioru rodiowego, WNT, Warszawa.
R y l e, M., V o n b e r g, D. D., 1948, Roy. Soc. Proc. (London), A193, 98.
S e e l y, S., 1968, Electronic Circuits, Holt, Rinehart and Winston.
S i f o r o v, W. I., 1974, Radiopriemnye ustrojstva, Sov. radio, M.
S w i e s z n i k o w, A. A., 1965, Podstawowe metody funkcji losowych, PWN, Warszawa.
T i u r i, M. E., 1964, IEEE Trans. Military Electronics, 8, 264.
V i l e s, R. S., 1977, Electronic Design, 7, 100.
W o l f, D., 1978, w zbiorze: Noise in Physical Systems, 122 (wyd. Wolf, D., Springer-Verlag, Berlin).
Z i e l, A. van der, 1954, Noise, Prentice-Hall, Englewood Cliffs, N. J.