POSTĘPY  ASTRONOMII
Tom XXV (1977), Zeszyt 3, 135–159

PRZEGLĄD  TORUŃSKICH  WYNIKÓW OBSERWACJI  SŁOŃCA  NA  CZĘSTOŚCI  127 MHz

A SURVEY OF THE 127 MHz TORUŃ SOLAR RADIO DATA Summary     This paper presents (i) a complete survey of mean monthly and mean yearly values of the flux density from the Sun, (ii) a review of outstanding occurrences observed at 127 MHz since 1958 at the Toruń Observatory. All data are based on the records of the Institute of Astronomy in Toruń and most of them were never publshed before. The data show a general agreement witth the 11-year solar activity cycle. A spectral analysis suggests that there also exists a 3.4 month periodicity in the declining part of the 20th cycle. The results of the past two years show that the minimum of solar activity in the 20th cycle occurred between Murch and July 1975 and not in 1976 as was previously suggested by solar spots and interplanetary events observations.     A theoretical model enabled to find the most essential component of disturbances in the measurements. The model also shows that the present antenna system is not satisfactory for this type of observations.     Some critical remarks concerning incompleteness of presented observations and some suggestions for the future observations are given.

1. UWAGI WSTĘPNE

Problemy związane z wpływem aktywności Słońca na zjawiska geofizyczne wymagają, jak wiadomo, ciągle nowych danych obserwacyjnych. Te ostatnie są tym bardziej wartościowe im dłuższy obejmują okres i, oczywiście, im bardziej są kompletne. Toruńskie pomiary pozostawiają wprawdzie wiele do życzenia pod względem kompletności i stabilności, ale ich atutem jest właśnie bogactwo materiału statystycznego, które wraz z unikalnością (wyniki te stanowią obecnie bodajże najdłuższy na świecie ciąg obserwacji Słońca na tak długich falach) czyni je znaczącymi. Zatem, niezależnie od tego, że obserwacje te spełniały i spełniają swoje zadanie jako służba Słońca, pożyteczne wydaje się podjęcie próby zebrania i uporządkowania wszystkich dostępnych danych, którymi dysponują Światowe Centra Danych (WDCs), lub które istnieją li tylko w archiwach Instytutu Astronomii UMK. Jest to niewątpliwie przedsięwzięcie trudne do zrealizowania, jednak gdyby się powiodło chyba równie trudno byłoby przecenić jego wyniki.

Pierwszym celem niniejszego przeglądu jest zapoznanie potencjalnych zainteresowanych z istniejącym materiałem obserwacyjnym. Towarzyszy temu cień krytyki, który jednak nie podważa istoty ani potrzeby takich obserwacji, lecz daje podstawę do stwierdzenia, że jest jeszcze wiele do zrobienia, by rezultaty były bardziej wartościowe.

Dotychczasowe wykorzystanie toruńskich obserwacji, jeśli nie liczyć bieżącego pożytku charakterystycznego dla służby, ogranicza się do kilku publikacji, w których analizuje się lub korzysta z danych i które w zasadzie były dziełem tylko pracowników Instytutu. Niewątpliwie duża w tym „zasługa” braku szerokiej informacji i łatwego dostępu do tych obserwacji. Fakt, że wyniki były zawsze dostarczane do niektórych centrów danych i do wybranych osób zainteresowanych niewiele kłóci się z tą opinią wobec niesystematyczności, które pojawiały się często w opracowywaniu i dystrybucji comiesięcznych raportów i które w końcowym rozrachunku okazały się przyczyną powstawania luk w powszechnie dostępnych publikacjach.

Przez wiele lat podstawową publikacją radiowych wyników obserwacji Słońca był „Quarterly Bulletin on Solar Activity” (QBSA), docierający obecnie do odbiorców z wynikami opóźnionymi o ponad rok. Tam też można znaleźć najbardziej kompletny, choć posiadający wiele braków, materiał dotyczący średnich dziennych gęstości strumienia promieniowania Słońca (tabele Flux Density) na częstości 127 MHz, poczynając od nr 124 tego „Biuletynu” zawierającego m.in. pierwsze toruńskie wyniki z paździeqlika 1958 r. Do września 1970 r. strumienie średnie były prezentowane w QBSA równolegle ze wskaźnikiem zmienności (Variability). Od tego momentu zmienność nie jest uwzględniana w żadnym międzynarodowym biuletynie. W miarę aktualny przegląd toruńskich wyników oceny tego parametru stanowi praca B o r k o w s k i e g o (1976b). Również w QBSA były publikowane dane o zjawiskach niezwykłych (Distinctive Events lub Outstanding Occurrences), jednakże toruńskie opracowania reprezentowane były tam tylko w sporadycznych przypadkach. Znakomita większość tych wyników pozostała jedynie w raportach miesięcznych, o ile zostały w ogóle odzyskane z zapisów. Poczynając od obserwacji ze stycznia 1975 r. wszystkie opracowane w Toruniu zjawiska są opisywane w amerykańskim miesięczniku „Solar-Geophysical Data” (SGD) z opóźnieniem pół roku. Praktycznie użyteczną listę źródeł toruńskich wyników można zamknąć na kilku przeglądach rocznej aktywności Słońca publikowanych na łamach „Acta Astronomica”, „Postępów Astronomii” i „Uranii” (ostatnio tutaj zamieszczane są także comiesięczne uwagi o wynikach obserwacji i radiowej aktywności Słońca). Spis najważniejszych ze wspomianych przeglądów znajduje się w pracy B o r k o w s k i e g o (1976a).

2. WYNIKI

Tabela 1

Toruńskie obserwacje Słońca na częstości 127 MHz — średnie miesięczne gęstości strumienia (10–22 W·m–2·Hz–l; kolumny I do XII), oraz dane roczne: procentowa ilość dni obserwacji (P), średni strumień (S), ilość zjawisk niezwykłych (Z), zmienność (V) i liczba Wolfa (R, wg danych z Zürichu)  Rok I II III IV V VI VII VIII IX X XI XII P S Z V R 1958 - - - - - - - - - 6,2 5,2 8,7 10,1 6,7 0,38 0,49 184,8 1959 9,2 8,5 11,7 6,5 6,5 6,0 8,5 26,0 8,0 4,5 21,0 12,1 83,6 11,0 0,70 0,89 159,0 1960 7,2 - - - - - - - 4,7 29,5 30,6 8,4 38,0 16,9 0,52 0,82 112,3 1961 6,0 5,1 6,5 4,9 4,5 6,5 10,7 6,8 4,7 4,9 3,0 4,2 91,5 5,7 0,39 0,42 53,9 1962 3,2 36,5 4,8 7,2 8,6 3,8 4,6 3,3 5,3 3,3 4,8 3,3 81,9 6,2 0,26 0,37 37,6 1963 5,2 4,3 3,4 4,8 3,9 5,9 2,9 5,0 4,3 6,5 3,7 3,9 74,8 4,4 0,10 0,19 27,9 1964 5,0 6,2 4,4 3,2 2,9 2,7 2,9 2,8 2,6 3,3 3,0 2,3 89,1 3,5 0,04 0,08 10,2 1965 2,7 3,5 3,2 2,2 2,2 2,2 2,2 2,0 2,3 2,5 2,1 1,8 85,5 2,4 0,06 0,10 15,1 1966 5,3 1,8 14,4 3,9 3,1 5,3 6,4 6,2 4,3 3,6 3,3 9,2 71,0 5,8 0,26 0,43 47,0 1967 5,3 14,4 6,0 4,8 9,5 5,3 5,5 8,6 5,6 4,1 17,5 5,7 83,0 7,2 0,67 0,80 93,8 1968 7,9 9,2 4,8 2,6 3,1 3,7 4,2 21,9 7,3 23,4 8,1 7,5 80,6 8,6 0,27 0,90 105,9 1969 16,9 11,5 3,4 3,8 15,9 7,l 2,7 2,7 2,7 4,l 6,l 3,8 74,8 7,0 0,31 0,74 105,5 1970 3,6 3,4 48,7 4,4 3,0 8,4 5,2 12,7 9,9 6,6 23,2 5,0 71,0 11,2 0,37 0,53 104,5 1971 49,0 5,5 4,7 10,5 5,3 4,2 5,3 46,9 3,6 4,7 4,3 5,0 74,8 12,5 0,38 0,81 66,6 1972 3,9 4,6 5,8 6,l 11,8 6,0 - 8,3 4,4 5,l 2,9 2,5 66,4 5,8 0,23 0,41 68,9 1973 - - - - - 3,3 2,3 2,2 7,4 3,2 6,3 39,2 4,2 0,03 0,07 38,0 1974 3,4 2,9 2,9 4,0 5,1 4,1 - 4,8 49,1 28,8 5,2 7,9 77,3 9,9 0,23 0,15 34,5 1975 6,8 2,7 4,l 3,9 3,4 3,l 2,9 13,1 3,8 3,1103,0 3,4 94,2 13,2 0,l9 0,04 15,5 1976 3,5 3,2 23,4 3,3 2,7 2,5 3,3 12,1 6,3 3,6 3,4 3,9 96,7 6,0 0,35 0,l3 12,6

Zestawienie to oparto na dziennikach obserwacji z wyjątkiem okresu od X 1958 do I 1960 r., dla którego podstawą były raporty miesięczne. Niewielkie różnice między prezentowanymi wielkościami a odpowiednimi liczbami znalezionymi w danych dziennych publikowanych w QBSA, w kilku przypadkach także wziętych z raportów miesięcznych — na ogół wynikają z błędów w tamtych źródłach oraz faktu, że średnie miesięczne zamieszczane w QBSA były obliczane ze średnich dziennych zaokrąglonych do liczb całkowitych (średnie w tab. 1 obliczono ze średnich dziennych podanych z dokładnością do 0,1 su; 1 su = 10^–22 W·m^–2·Hz^–l). Niestety, nie wszystkie średnie miesięczne w tab. 1 są wewnętrznie zgodne. Wynika to z różnych założeń przyjmowanych w różnych okresach dla redukcji danych obserwacyjnych. Strumień Słońca obliczano zawsze na podstawie obserwacji radioźródła Cassiopeia A z uwzględnieniem źródła Cygnus A. W pierwszych latach obserwacji przyjmowano, że na częstości 127 MHz gęstość strumienia Cas A wynosi 1,5 su, a Cyg A — 1 su (W h i t f i e l d 1959). W okresie 1972,0 – 1974,5 przyjmowano na te wielkości odpowiednio 1,67 i 1,07 su. Od lipca 1974 r. w Toruniu stosuje się skalę kalibracyjną opartą na ostatnich wynikach pomiarów absolutnych, w której strumień Cas A na początku 1977 r. miał gęstość 1,407 su i spada o 1,22% w stosunku rocznym (B o r k o w s k i 1975; D e n t i in. 1974). Jeśli oprzeć się na powyższych danych i przyjąć, że ostatnio stosowana skala jest prawdziwa, wówczas współczynniki korygujące wszystkie wcześniejsze wyniki pomiarów strumienia dla kolejnych lat od 1958 do 1974 będą następujące: 1,17; 1,16; 1,15; 1,13; 1,12; 1,11; 1,09; 1,08; 1,07; 1,05; 1,04; 1,03; 1,02; 1,00; 0,89; 0,88 i 0,87. Współczynniki te zostały obliczone dla środka każdego roku z wyjątkiem 1974 r., dla którego czynnik 0,87 dotyczy tylko jego pierwszej połowy. Przedstawione tutaj wyniki nie uwzględniają tych poprawek. Jak wynika z niektórych prac, również obecne założenia mogą okazać się nieścisłe (E r i c k s o n, P e r l e y 1975; R e a d 1976; W i e l e b i n s k i l976; T s e y t l i n i in. 1976; K a n d a 1976). Trzeba także dodać, że podane współczynniki nie uwzględniają przyczynków związanych ze zjawiskiem dudnienia promieniowania Cas A i Cyg A (wynika ono z małej odległości kątowej tych źródeł w stosunku do charakterystyki anten), co czyni kalibrację w oparciu o obserwację dowolnego z tych źródeł obarczoną pewnym, możliwym do oceny błędem. Ponadto, na skutek omawianych dalej odbić promieniowania Słońca od ziemi, jego pomiary są silnie zakłócane, wobec czego praktycznie wszystkie wyniki z ostatnich kilku lat (od jesieni 1972 r.) należy traktować jako prowizoryczne.

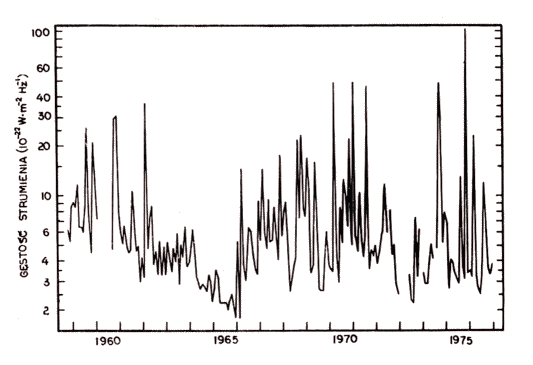Rys. 1. Średnie miesięczne gęstości strumienia promieniowania Słońca obserwowane na częstości 127 MHz w Obserwatorium Toruńskim

W tab. 2 przedstawiono podsumowanie wyników opracowania zjawisk niezwykłych. Oczywiste jest, że liczby te nie mają istotnego znaczenia statystycznego ze względu na niekompletność wynikającą z obiektywnych częściowo trudności. Częściowo, gdyż okazuje się, że szereg luk w tych wynikach powstała w różnych okresach z przyczyn, które można określić terminem „brak zainteresowania”. Widać to wyraźnie w pracy G a w r o ń s k i e j (1977), z której wynika m.in., że liczby z podane w tab. 2 powinny na ogół być zwiększone.

Tabela 2

Toruńskie obserwacje Słońca na częstości 127 MHz — ilość zjawisk niezwykłych (z) i dni obserwacji (n) w miesiącu i roku (Z i N, odpowiednio) Mies.: I II III IV V VI VII VIII IX X XI XII Rok Rok z n z n z n z n z n z n z n z n z n z n z n z n Z N 1958 - - - - - - - - - - - - - - - - - - 3 3 4 19 7 15 14 37 1959 6 5 3 14 22 24 12 29 32 31 30 30 18 29 22 31 11 29 18 29 28 30 10 24 212 305 1960 18 29 - - - - - - - - - - - - - - 18 24 16 29 11 30 9 27 72 139 1961 11 23 6 21 7 29 5 30 4 30 14 30 12 29 14 30 22 30 18 31 7 22 11 29 131 334 1962 3 26 8 15 7 30 14 21 4 22 1 25 2 23 0 24 16 27 8 31 8 24 7 31 78 299 1963 4 28 0 28 0 31 5 26 4 28 8 29 0 27 3 4 3 7 0 14 0 24 1 27 28 273 1964 4 25 4 29 2 31 0 24 0 27 0 28 0 30 0 27 0 29 0 26 0 29 2 21 12 326 1965 4 23 1 23 1 21 0 30 0 29 2 29 3 30 0 29 4 28 2 23 0 20 1 27 18 312 1966 3 27 0 17 10 25 7 22 1 23 2 18 10 27 6 20 4 10 2 24 5 23 17 23 67 259 1967 50 30 20 22 21 29 13 30 13 28 15 29 12 30 16 15 2 18 18 25 11 18 12 29 203 303 1968 17 30 5 19 4 28 1 29 1 23 3 26 1 27 13 24 6 24 8 28 11 21 11 16 81 295 1969 17 28 9 24 4 25 5 22 5 23 6 23 6 25 11 27 13 21 6 27 18 2 10 84 273 1970 2 19 11 19 24 20 4 20 13 20 13 22 11 20 9 25 5 26 0 25 1 22 2 21 95 259 1971 9 23 7 23 7 22 12 16 5 24 4 18 3 19 11 24 12 26 10 27 15 29 8 22 103 273 1972 5 27 7 23 6 25 11 29 8 28 10 29 - - 2 13 5 22 1 16 16 15 55 243 1973 - - - - - - - - - - 15 22 4 25 0 24 1 31 0 26 5 143 1974 30 26 30 30 30 27 - - 0 5 22 18 20 31 19 30 5 25 64 282 1975 8 29 1 27 4 29 6 28 4 31 2 27 4 26 16 31 0 26 0 29 14 30 8 31 67 344 1976 13 31 1 29 19 31 6 27 1 30 1 28 1 28 40 31 14 28 6 31 9 30 13 30 124 354

Puste miejsca w tab. 1 i 2 oznaczają brak opracowań wskazanych parametrów, mimo że istnieją zapisy obserwacji. Średnie roczne (tab. 1) obliczono na podstawie tych tabel zastępując puste miejsca i braki obserwacji zerami. Są to średnie ważone ilością dni obserwacji. Średnie zmienności (V) obliczono podobnie w oparciu o wyniki podane przez B o r k o w s k i e g o (1976b), uzupełniając o następujące średnie miesięczne z obserwacji późniejszych: 0,00; 0,10; 0,00; 0,55; 0,04; 0,00; 0,00; 0,07; 0,48; 0,14; 0,06; 0,03 i 0,07 (odpowiednio od XII 1975 do XII 1976 r.) oraz pominiętą w tamtej pracy średnią z grudnia 1972 r. — 0,33. Tych samych danych użyto do wyliczenia odpowiednich wielkości do tab. 3. Przytoczone dla porównania liczby Wolfa zostały zaczerpnięte z publikacji „Solar Terrestrial Physics and Meteorology” (1975) i uzupełnione o ostatnie wyniki końcowe i prowizoryczne zamieszczane w SGD (1976 i 1977). Również dla porównania obliczono średnie miesięcy gęstości strumienia na częstości 1000 MHz do tab. 3, do czego podstawą było „Complete Summary” ( 1975) oraz raporty miesięczne z Toyokawa Observatory (lata 1975 i 1976).

3. ANALIZA I DYSKUSJA WYNIKÓW

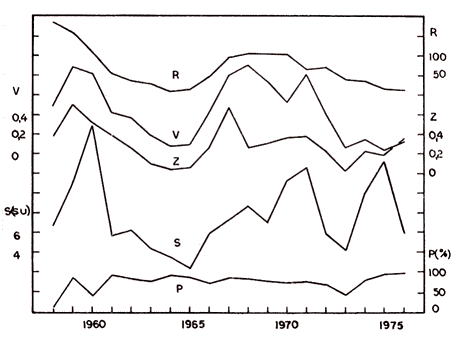Rys. 2. Średnie roczne: liczby Wolfa (R), wskaźniki zmienności (V), ilość wybuchów (Z) i gęstości strumienia (S) oraz procentowa liczba dni obserwacji (P)

Gdyby połączyć wyraźne odstępstwo przebiegu strumienia od przebiegu, jaki sugerują plamy słoneczne od 1973 r. z faktem całkowitej wymiany systemu odbiorczego w tym okresie, to nasuwa się wątpliwość, czy w metodyce opracowywania obserwacji nie tkwi obecnie jakiś gruby błąd. Znaczący jednak wydaje się być inny fakt. W listopadzie 1975 r. zanotowano największe poziomy promieniowania ciągłego w całej historii toruńskich obserwacji. Tak np. średnia z dnia 20 XI wyniosła 1600 jednostek strumienia, co dorównuje poziomom wielkich wybuchów. Stąd też średnia tego miesiąca była również rekordowo duża — dwukrotnie większa od dotychczasowego „rekordu”. Spowodowało to dalej, że średnia roczna wzrosła aż do wartości 13,2 su (największa od 1960 r.), gdy tymczasem średnia z pozostałych 11 miesięcy tego roku wynosi tylko 4,6 su. Ten sam fakt powoduje, że średnia listopada jest wyższa od pozostałych (tab. 3, rys. 3). Potwierdzenie anomalności tych rezultatów dają obserwacje na częstości 100 MHz (Gorki), z których średnia omawianego miesiąca wyniosła 70 su (QBSA 1976). Trzeba jednak pamiętać, że wyniki toruńskie i wspomnianej stacji zawsze istotnie się różniły. Interesujące w tych rozbieżnościach jest to, że toruńskie wyniki pomiarów są zaniżone względem rosyjskich w okresach spokojnego Słońca, natomiast zawyżone w czasie wzmożonej aktywności (dla dużych strumieni). Sugeruje to, że odpowiedzialna za ten efekt może okazać się nieliniowość charakterystyki wzmocnienia któregoś z odbiorników (niewłaściwa kalibarcja odbiornika).

Tabela 3

Średnie: strumień (S), zmienność (V) i ilość zjawisk niezwykłych (Z) wg obserwacji toruńskich obliczone dla poszczególnych miesięcy. W kolumnie S(1000) podano odpowiednie strumienie na częstości 1000 MHz wg obserwacji japońskich (Toyokawa Observatory) Mie- 29 X 1958 - 31 XII 1976 1 VIII 1964 - 31 VII 1976 Obserwacje Średnie Obserwacje Średnie siąc Dni % S V Z Dni % S V Z S(1000) I 433 77,6 7,8 0,57 0,40 297 79,8 9,4 0,58 0,43 72,6 II 359 70,5 6,9 0,42 0,23 252 74,3 5,6 0,46 0,25 71,6 III 430 77,1 8,9 0,43 0,32 285 76,6 10,4 0,54 0,35 70,4 IV 413 76,5 4,6 0,33 0,24 283 78,6 4,3 0,34 0,23 69,1 V 427 76,5 5,6 0,36 0,22 289 77,7 5,9 0,36 0,18 70,6 VI 433 80,2 6,2 0,35 0,26 301 83,6 4,4 0,32 0,19 69,3 VII 392 70,3 4,7 0,41 0,21 280 75,3 3,6 0,36 0,18 68,5 VIII 385 69,0 11,7 0,43 0,43 265 71,2 11,4 0,44 0,33 68,8 IX 417 77,2 7,1 0,49 0,38 272 75,6 7,8 6,42 0,27 69,1 X 480 85,6 8,4 0,46 0,28 312 83,9 8,2 0,48 0,22 69,3 XI 461 80,9 15,0 0,39 0,31 282 78,3 17,3 0,37 0,27 69,2 XII 423 71,8 5,4 0,40 0,30 240 64,5 4,9 0,34 0,28 70,2 Razem 5053 76,1 7,8 0,42 0,30 3358 76,6 7,8 0,42 0,26 69,9

Okazuje się, że ryzykowne wciąż pozostaje przewidywanie przebiegu aktywności Słońca, nawet na krótki okres (C o l e 1973; C o v i n g t o n 1974, 1976; S z y m a ń s k i 1976; B o r k o w s k i, K ę p a 1976). Istnieje jednak kilka przesłanek na to, że minimum aktywności Słońca w 11-letnim cyklu wystąpiło w lipcu ub.r. (np. MONSEE Bulletin 1976, SGD 1977). Do nich dołączają ostatnie wyniki obserwacji plam słonecznych oraz promieniowania na krótszych falach radiowych, na których wyraźnie widać składową wolnozmienną (SVC). Przegląd toruńskich wyników w zasadzie nie daje poparcia temu sądowi. Jeśliby wnioskować o minimum aktywności Słońca na tych falach z przebiegu średnich rocznych zinienności i ilości wybuchów, to — jak wskazuje

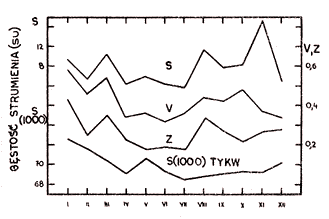Rys. 3. Średnie parametry obliczone dla poszczególnych miesięcy z okresu VIII 1964 – VII 1976 r.: S, V i Z odpowiadają strumieniowi, zmienności i gęstości zjawisk niezwykłych na 127 MHz, a S(1000) — strumieniowi na 1000 MHz

tab. 1 — rok 1975 okaże się najmniej aktywny (wyłączając ze względów oczywistych rok 1973). Jeśli ponadto potraktować zajwiska z XI 1975 jako „wybryk natury” wówczas także średni sturmień okaże się w tym roku mniejszy niż w sąsiednich. Bilższy wgląd w wyniki każe moment minimum umieścić pomiędzy marcem i lipcem 1975 r. Zwraca także uwagę stosunkowo głębokie minimum w średnich dziennych w okresie IV–VII 1976 r. (rys. 6 i dalsze), które zachęca do wniosku o jego związku z generalnym minimum aktywności Słońca, jednakże, choćby w świetle odbić, byłby to wniosek nieco przedwczesny.

Tabela 3 i rys. 3 zawierają statystyki poszczególnych miesięcy w obserwacjach toruńskich z wyszczególnieniem okresu obejmującego domniemany 20 cykl aktywności Słońca. Wahania średnich parametrów miesięcy w wynikach toruńskich (57–175% wartości średniej) znacznie przewyższają odpowiednią wielkość znalezioną dla strumienia na częstości 1000 MHz (6%). Najbardziej równomiernie po miesiącach w 20 cyklu rozłożyła się zmienność, ale różnica między średnią stycznia i czerwca osiągnęła prawie 62% średniej całego cyklu. Jest to świadectwo dużej dynamiki tych parametrów promieniowania Słońca na falach metrowych. Potwierdzeniem tej opinii może być też duże „zaszumienie” widm mocy (rys. 4).

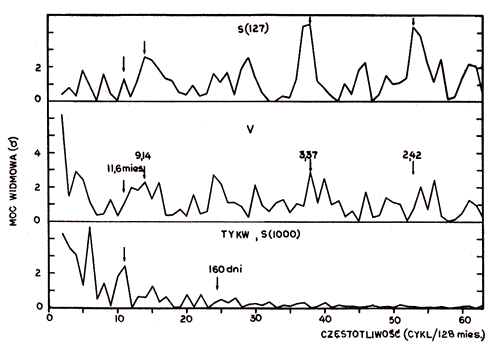Rys. 4.Widma mocy dla średnich miesięcznych strumieni i zmenności na 127 MHz oraz strumienia na 1000 MHz (Toyokawa) obliczone dla okresu XI 1961 – VI 1972 r. Wyniki są znormalizowane do odchylenia standardowego (σ)

Estymatory widmowej gęstości mocy oparto na transformatach Fouriera wykonanych metodą szybką (STF lub FFT; C o c h r a n i in. 1967; S o b k o w s k i 1975). Względy techniczne zadecydowały o ograniczeniu ciągów analizowanych danych dą 128 punktów. Wyniki zostały znormalizowane do odchylenia standardowego składowych widma o częstotliwościach większych niż 1 cykl/128 miesięcy. Na rys. 4 dla przejrzystości pominięto częstotliwości 0 i 1, które reprezentują składowe będące odbiciem wartości średniej i 11-letniej cykliczności (odpowiednio). Ta ostatnia składowa najwyraźniej występuje w widmie strumienia na częstości 1000 MHz (przewyższa 290 razy odchylenie standardowe σ). W toruńskich wynikach składowa ta wynosi 9,2 σ dla strumienia (S) i 41,2 σ dla zmienności (V). Poziom 3 σ przekracza również linia odpowiadająca okresowi ok. 3,4 miesiąca w widmie strumienia. Jest ona też widoczna, chociaż nieco słabiej, w widmie zmienności. Podobne analizy wykonane dla innych przedziałów czasu, z mniejszą rozdzielnością i z zastosowaniem funkcji okna typu Tukeya (S c h w a r t z, S h a w 1975; B e n d a t, P i e r s o l 1976) prowadzą do znacznie różnych wyników. Na tej podstawie można zaniedbać inne linie widmowe widoczne na rys. 4, dotyczące obserwacji toruńskich, być może z wyjątkiem wskazanych tam prążków odpowiadających okresom 11,6, 9,1 i 2,4 miesiąca. Ta rozbieżność rezultatów analizy widmowej i porównania z wynikami uzyskanymi przez E l- R a e y a i A m e r a (1975) (stwierdzają oni m.in. 160-dniową periodyczność w analizowanych tu wynikach z Toyokawy) oraz C u r r i e g o (1973) wobec niekompletności toruńskich pomiarów każą sądzić, że lepszym estymatorem widmowej gęstości mocy — zwłaszcza od strony małych częstotliwości widmowych — okaże się wynik zastosowania niedawno opracowanej metody maksymalnej entropii (np. U l r y c h 1972).

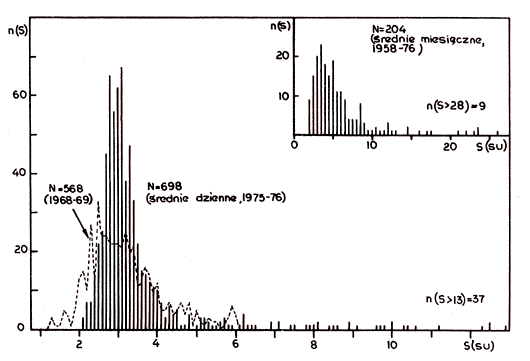
Rys. 5. Rozkład liczby średnich dziennych i miesięcznych n(S) w funkcji amplitudy strumienia S w obserwacjach toruńskich

Wgląd w rozkład amplitud średnich strumieni dziennych (rys. 5) daje dodatkowy argument na to, że w 1975 r. aktywność Słońca na 127 MHz osiągnęła minimum w części spadkowej 20 cyklu. Świadczy o tym procentowa ilość dni, w których obserwowano zwiększone strumienie promieniowania. Tak np., w 1975 r. zanotowano 7,6% średnich dziennych większych od 7 su, gdy w 1976 r. było ich 10,5% (jakościowo ten sam rezultat utrzymuje się dla średnich większych od dowolnej z wartości wziętych z przedziału 6–16 su). Porównanie histogramów amplitud średnich dziennych w latach 1975–1976 i 1968–1969 (rys. 5) sugeruje, że obecne pomiary promieniowania Słońca spokojnego są stabilniejsze (mówi o tym wyraźnie mniejszy rozrzut wokół mediany, która w latach 1975–1976 wyniosła 3,1 su, a w latach 1968–1969 — 3,2 su). Dodać też warto, że w l. 1968 i 1969 średnich dziennych większych od 7 su było odpowiednio 17,3 i 9,9%, co — wobec bliskości tych lat okresowi maksimum aktywności Słońca — znacznie osłabia argument o obecnym minimum.

4. WYNIKI Z LAT 1973–1976

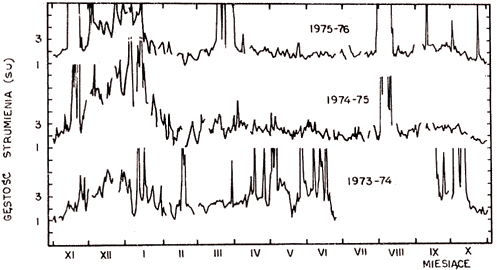Rys. 6. Wyniki toruńskich pomiarów strumienia promieniowania Słońca na częstości 127 MHz w latach 1973–1976 wykonanych w 6 listku interferencyjnym (ok. godz. 9 czasu uniwersalnego). Dane z 1973 r. pochodzą z innej serii opracowań

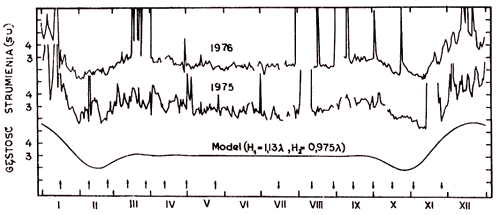Rys. 7. Porównanie rzeczywistych zmian strumienia obserwowanego na kierunku 9 listka interferencyjnego (południe prawdziwe) w latach 1975–1976 z przebiegiem teoretycznym. Strzałki u dołu rysunku wskazują momenty i kierunki przestawiania nachylenia anten (co 6° deklinacji Słońca)

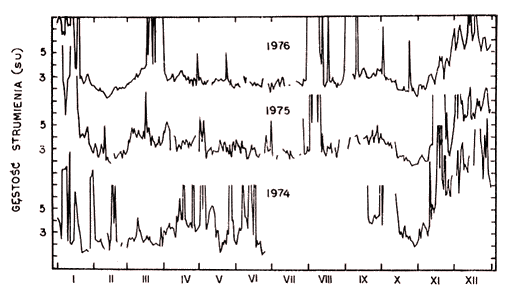
Nawet bardzo pobieżny przegląd obserwacji w ostatnich kilku latach pozwala zauważyć silny wpływ pór roku na wyniki. Dla zilustrowania tego efektu na rys. 6–9 przedstawiono roczne przebiegi wyników pomiaru strumienia promieniowania Słońca w kilku, reprezentatywnych dla charakterystyki systemu antenowego, listkach interferencyjnych w latach 1973–1976. Listkom przyporządkowano numery zgodnie z upływem czasu w ten sposób, że listek nr 9 pojawia się na ok. 10 min. przed południem prawdziwym w Piwniacach. Prezentowane na tych rysunkach wyniki nie pokrywają się z wynikami publikowanymi miesięcznie w dostępnych biuletynach. Obliczono je przy założeniu, że charakterystyka systemu antenowego w rozpatrywanym okresie nie ulega zmianie. Na wszystkich przebiegach wyróżnia się składnik wolnozmienny o rocznej powtarzalności mający trzy maksima, z których najwyższe przypada na okres najmniejszej deklinacji Słońca, oraz trzy minima z najmniej znaczącym z okresu maksimum deklinacji Słońca (czerwiec). Jakościowo taki sam przebieg uwidacznia się w uśrednionych całodziennych wynikach (średnie obejmujące listki od 5 lub 6 do 17). Pokazuje to rys. 9. Z pożytkiem dla późniejszych rozważań można zauważyć, że minima w lutym (rys. 10) oraz w październiku lub listopadzie, jak również niższe maksima z marca i września, pojawiają się tym później wiosną i tym wcześniej jesienią im większy jest kąt pomiędzy płaszczyzną południka miejscowego i kierunkiem listka charakterystyki anten.

Rys. 8. Wyniki pomiarów strumienia w latach 1974–1976 w 12 listku interferencyjnym (przed lub ok. 12 godz. UT)

Symetria zmian względem ekstremalnych deklinacji Słońca oraz zależność momentów pojawiania się ekstremów strumienia od kierunku na sferze niebieskiej (symetria względem południka) przemawiają za odbiciową ich interpretacją. Wprawdzie nie badano jeszcze wpływu tego czynnika na wcześniejsze wyniki obserwacji, jednak jeśli on istniał przed 1972 r., to w znacznie mniejszym stopniu niż obecnie. Wiąże się to z szerokością wiązek charakterystyki anten w płaszczyźnie H, w której następują odbicia. Od jesieni 1972 r. do służby Słońca używa się anten o szerokości połówkowej ok. 65°, z czego już wynika, że w okresie najmniejszej deklinacji Słońca promieniowanie odbite od płaskiego terenu przed antenami w poziomej składowej polaryzacji nawet w południe jest odbierane ze skutecznością ok. 50% w stosunku do sygnału przychodzącego z kierunku największego wzmocnienia.

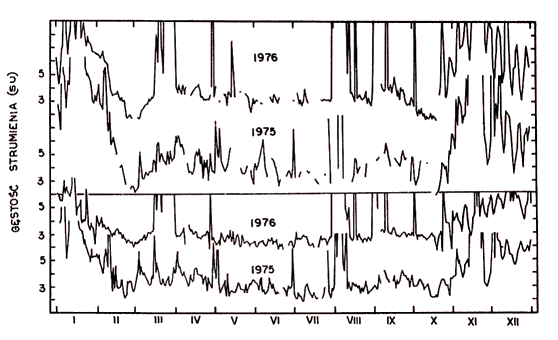
Rys. 9. Przebiegi strumienia obserwowanego w 15 listku interferencyjnym (u góry) i średnie dzienne (9–15 UT) w latach 1975–1976

Podczas opracowywania obserwacji łatwo jest zauważyć, że w czasie zimy istnieją ponadto względnie szybkie (dla kontrastu będą dalej zwane oscylacjami) zmiany strumienia mierzonego na poszczególnych listkach interferencyjnych mające okres kilku (4 – 10) dni. Zgodność pojawiania się ekstremów tych oscylacji w kolejnych latach (rys. 11a) i korelacja pomiędzy poszczególnymi iistkami niezbiecie świadczy o nieprzypadkowym ich charakterze i każe odrzucić m.in. wpływ aktywności Słońca jako jedną z możliwych interpretacji. Wyjaśnienia można by szukać w odbiciach promieniowania od dalekich przedmiotów terenowych (w odległościach rzędu 100 m), jak to sugeruje duża częstotliwość oscylacji w obecności małych zmian deklinacji Słońca. Mimo że istnieją również inne przesłanki „za”, to jednak wizja lokalna jest tym, co każe wątpić w takie wyjaśnienie.

Brak zadowalającego wytłumaczenia zjawiska oscylacji usprawiedliwia zwrócenia uwagi na dwa jeszcze fakty z tym związane. Szczególnie nieprzyjemne rozmiary osiągają oscylacje w środku zimy (grudzień) na kilku skrajnych popołudniowych listkach (rys. 9 i 11b). Inną charakterystyczną własnością jest niemal całkowity ich zanik jesienią, gdy wiosną widoczne są jeszcze w marcu. Pierwszy z faktów kojarzy się z niesymetrycznym względem kierunku południa ukształtowaniem terenu przed antenami, drugi zaś — z różnymi warunkami atmosferycznymi (wilgotność gruntu) wiosną i jesienią. Oba jednak, o ile te skojarzenia są słuszne, ponownie kierują myśl na odbicia.

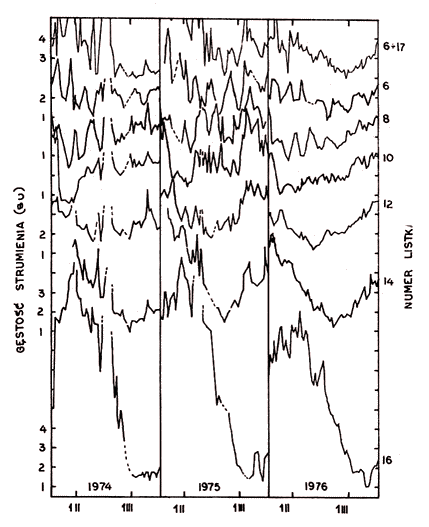Rys. 10. Przebiegi strumienia obserwowanego w listkach 6, 8, 10, 12, 14, 16 oraz średnie dzienne (z listków 5 lub 6–17) w dniach 20 I – 16 III lat 1974, 1975 i 1976

Od czasu uruchomienia obecnie używanych anten do września 1975 r. w opracowaniach obserwacji nie uwzględniano wpływu promieniowania odbitego. Efektywne zmiany wag listków interferencyjnych były poprawiane ze statystycznych odchyłek względem listka centralnego

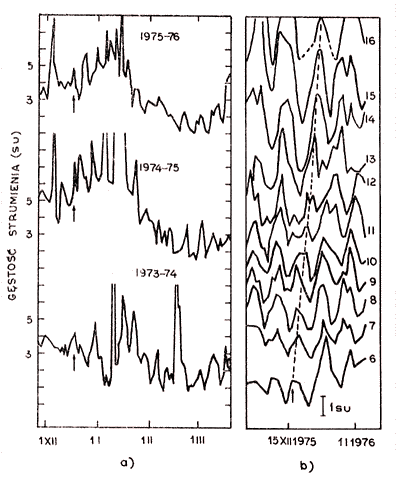Rys. 11. Przykłady oscylacji strumienia w okresie zimy w 5 listku intereferencyjnym (a) i ich porównanie w listkach od. 6 do 16 (b). Strzałki wskazują jedno z maksimów podejrzane o wspólne pochodzenie

(9; B o r k o w s k i 1976a). Nie eliminowało to, oczywiście, zmian wagi tego listka, a w końcowym rezultacie — zmian średnich dziennych wywołanych odbiciami. Poczynając od października 1975 r. redukcja danych odbywa się po szczegółowej analizie przebiegu strumienia obserwowanego w każdym listku z uwzględnieniem wyników obserwacji w analogicznych okresach ubiegłych lat. Na skutek braku absolutnego poziomu odniesienia dla strumieni w okresie wrzesień–kwiecień koniecznością staje się jednak założenie w to miejsce poziomu strumienia Słońca spokojnego (przyjmuje się nań 3 su). Może to w pewnych przypadkach prowadzić do skutecznego wyeliminowania długoczasowych (dłuższych niż ok. 10 dni) nieznacznych wzrostów lub spadków promieniowania Słońca, dlatego wszystkie wyniki pomiarów strumienia uzyskane po ostatniej wymianie anten należy traktować jako prowizoryczne. Poprawienie wyników powinno być wykonane po zebraniu dostatecznie obfitego materiału statystycznego w oparciu o analizę efektów odbiciowych z uwzględnieniem przebiegu aktywności Słońca obserwowanego na innych częstościach.

5. WIĘCEJ O ODBICIACH

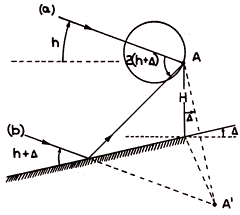Rys. 12. Szkic pokazujący mechanizm powstawania zakłóceń odbioru wywołanych przez promieniowanie odbite od ziemi, na przykładzie jednej anteny. Okrąg symbolizuje charakterystykę kierunkową anteny (A)

Na rys. 12 pokazano sytuację, w której do anteny odbiorczej A oprócz promieniowania padającego wprost (a) dociera też wiązka odbita (b) od powierzchni ziemi przed anteną (rozważana jest tu tylko składowa liniowa polaryzacji fali, prostopadła do rysunku). Z geometrii zjawiska łatwo zauważyć, że różnica dróg (wyrażona w długościach fali λ) przebytych przez oba promienie wyniesie 2·H·cosΔ·sin(h + Δ), gdzie: H jest wysokością środka promieniowania anteny nad ziemią (w λ), Δ — kątem nachylenia płaszczyzny odbijającej względem poziomu, a h — wysokością źródła promieniowania. Pomija się tutaj skończoną rozciągłość źródła oraz skończoność wstęgi odbieranych częstości, gdyż dla toruńskiego przypadku są one zaniedbywalne (Dodatek, B o r k o w s k i 1976a). Odpowiednia do przebytych dróg różnica faz sygnałów będzie większa o π (180°), ponieważ faza padającej fali w rozpatrywanej polaryzacji przy odbiciu zostaje odwrócona. W przypadku interferometru dwuantenowego o bazie d (w λ) będą cztery wiązki, których względne fazy wyniosą:

Ψo = 0, Ψ1 = 4πH1cosΔ1sin(h + Δ1) + π (wiązka odbita), Ψ2 = 2π{d[sinδsinδo + cosδcosδocos(t – to)] + D}      oraz Ψ3 = Ψ2 + 4πH2cosΔ2sin(h + Δ2) + π (wiązka odbita)

(1)

gdzie: indeksami 1 i 2 odróżniono wysokości obu anten i odpowiednie nachylenia terenu, δ_o i t_o oznaczają współrzędne równikowe bazy (deklinacja i kąt godzinny), δ i t — położenie źródła promieniowania w tychże współrzędnych, a D — różnicę dróg sygnałów w liniach przesyłowych (od anten do odbiornika) wyrażoną również w λ. Wielkości Ψ_o i Ψ₂ opisują zależności fazowe interferometru przy zaniedbaniu odbić.

Ograniczając nieco ogólność można przyjąć, że średnie amplitudy wszystkich czterech wiązek początkowo są jednakowe. Zróżnicowanie ich nastąpi wskutek strat przy odbiciu oraz nieizotropowości charakterystyk anten, Ten pierwszy czynnik silnie zależy od aktualnie panujących warunków atmosferycznych. Do obliczeń przyjęto zależność od kąta padania opracowaną dla tzw. dobrej gleby (ε = 10, σ = 0,01 S/m) na podstawie pracy P i c q u e n a r d a (1974 ): R_i = 0,864 – 0,0043(h + Δ_i), gdzie h + Δ_i, (i = 1,2) wyrażone jest w stopniach. Dla wiązek odbitych w dalekim polu (strefa Fraunhofera) tłumienie wynikające z charakterystyki anten dobrze przybliża czynnik cos²2(h + Δ_i) (rys. 12). Z faz (1) i powyższych przybliżeń można wyeliminować wysokość h korzystając ze znanych zależności trygonometrii sferycznej (zachodzi: sin h = sinψsinδ + cosψcosδcos t, gdzie ψ jest szerokością geograficzną miejsca obserwacji), co już pozwala skorzystać z zależności wyprowadzonej w Dodatku dla obliczenia przebiegu obserwacji źródła punktowego w funkcji jego współrzędnych równikowych i w obecności odbić. Ze względu na nieregularność rzeźby terenu dla toruńskiego interferometru najbardziej wiarogodne wydają się być chwilowo jedynie modele obliczone dla małych kątów godzinnych (obserwacje w pobliżu południa prawdziwego w przypadku Słońca). Praktyczne obliczenia wykonano w oparciu o przekształcenie:

V = S[(1 + Q1cosΨ1 + cosΨ2 + Q2cosΨ3)2 + (Q1sinΨ1 + sinΨ2 + Q2sinΨ3)2],

(2)

gdzie: Q_j = R_icos²2(h + Δ_i), i = 1, 2 są amplitudami pola, elektrycznego fal odbitych, a S jest średnim strumieniem Słońca spokojnego (przyjęto S = 3 su). Na parametry charakteryzujące toruński instrument położono następujące wartości: H₁ i H₂ z przedziału 0,8 – 1,5 λ, Δ₁ = 5°, Δ₂ = 0°, δ_o = 0°, t_o = 90°, d = 10 λ oraz D = 0,5 λ. Jeden z modeli, odpowiadający obserwacji w 9 listku interferencyjnym, przedstawia rys. 7.

Chociaż generalnie wyniki obliczeń teoretycznych przebiegów obserwacji Słońca w ciągu roku są zgodne z obserwacjami, to jednak istnieją różnice, których nie można złożyć na karb uproszczeń modelu czy też niedokładności parametrów interferometru. Z modelu wynika np, że gdy deklinacja Słońca osiągnie taką wartość, że promieniowanie odbite będzie dochodziło do anten pod kątem ok. 90° (względem kierunku maksimum wzmocnienia), wówczas jego wpływ powinien znikać przynajmniej tak, jak to sugeruje charakterystyka promieniowania anten (cosinus tego kąta w czwartej potędze). Łatwo skądinąd pokazać, że w takim przypadku odbicie następuje w pobliżu granicy dalekiego pola, gdzie przestają obowiązywać charakterystyki określone dla tamtego pola. Stąd prawdopodobnie wynika zaskakujący fakt wystąpienia minimum w obserwowanych strumieniach promieniowania Słońca w środku lata (kwiecień – sierpień), w czasie, gdy promieniowanie odbite dochodzi do anten pod kątem większym niż 90°. Oznacza to, że dostaje się ono tam przez listki boczne charakterystyki anten, a te w dalekim polu są przynajmniej 80-krotnie (w mocy) słabsze od głównego (B r o w n 1974; Andrew Corp. 1966), gdy tymczasem depresja strumienia obserwowanego wynosi (ostrożnie oceniając) ok. 10%. Biorąc jeszcze pod uwagę współczynnik odbicia (ok. 0,5 przy tych kątach padania) trudno jest ustrzec się wniosku, że to letnie minimum jest wynikiem w zasadzie tylko faktu, że wysokość umieszczenia anten nad ziemią jest mniejsza od odległości dalekiego pola (ok. 1 λ względem ok. 2 λ dla zwykle przyjmowanej granicy dalekiego poła). Dla poparcia tych rozważań na rys. 13 pokazano pośredni rezultat obliczania modelu obserwacji w obecności odbić — dla anten bezkierunkowych i ze 100% skutecznością odbicia, dzięki czemu wyniki są wolne od nieokreśloności charakterystyk anten i współczynnika odbicia. Widać z nich, że kderunek wpływu odbić letnich jest zgodny z tym, co się obserwuje (zaniżenie wyników pomiarów).

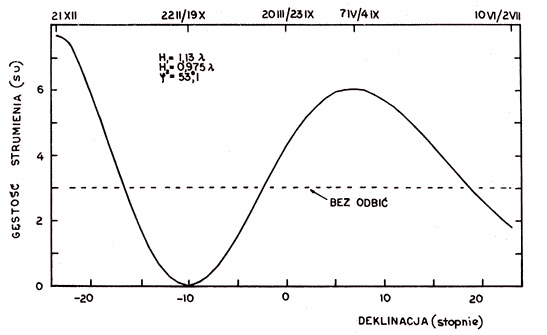Rys. 13. Teoretyczny przebieg strumienia obserwowanego w południku za pomocą interferometru o izotropowych antenach w obecności odbić, ze współczynnikiem 1, w funkcji deklinacji źródła (na górnej skali zaznaczono niektóre momenty odpowiadające deklinacji Słońca)

Analizując obserwowane przebiegi w 9 listku (rys. 7) w lutym i na przełomie października i listopada nietrudno wyróżnić nieoczekiwane wzrosty strumienia, kłócące się z modelem, Być może, że przyczynek do interpretacji tej rozbieżności tkwi w fakcie, że jest to okres, kiedy odbicia następują pod kątami bliskimi kątowi Brewstera. Przy przejściu przez ten kąt następuje odwrócenie fazy składowej pola elektrycznego, leżącej w płaszczyźnie padania. Jeżeli płaszczyzna ta nie jest prostopadła do kierunku polaryzacji anteny, wówczas składowa taka może być również odebrana. W danym przypadku rzeźba terenu sprzyja takiej możliwości.

Z przeprowadzonej dyskusji w tym punkcie wynikają dwa ważne wnioski. Po pierwsze, charakterystyki obecnie używanych anten są zbyt szerokie w płaszczyźnie H, co powoduje, że promieniowanie odbite przed antenami jest w znaczącym stopniu odbierane. Po drugie, wysokość umieszczenia anten jest zbyt mała, czego efektem jest obecność wpływu odbić na wyniki w ciągu całego roku. Godzi się jednak nadmienić, że ten czynnik nie jest tak istotny jak pierwszy, o czym przekonują wcześniejsze obserwacje — za pomocą anten o porównywalnej wysokości, lecz o węższej wiązce.

6. ZAMIAST ZAKOŃCZENIA

Tabela 4

Rozkład na dni tygodnia całodziennych braków w obserwacjach w okresie 11 IX 1974 – 31 I 1977 11 IX - 11 IX 1974 Okres 31 XIII 1975 1976 - 31 I 1977 1968-1969 Dzień 1974 dni % dni % Niedziela 3 7 4 15 34,1 29 17,8 Poniedziałek 3 5 7 16 36,4 36 22,1 Wtorek - 1 - 1 2,3 33 20,2 Środa - 3 1 4 9,1 13 8,0 Czwartek 1 3 - 4 9,1 18 11,0 Piątek - 1 - 1 2,3 17 10,4 Sobota 1 1 - 3 6,8 17 10,4 Razem dni/% 8 21 12 44 5,0 163 22,3

Tabela 5

To samo co w tab. 4, ale wg przyczyn Okres-> 1974 1975 1976 11 IX 1974 - 31 I 1977 Przyczyna (dni)-> (112) (365) (366) (874) Brak obsługi 3 14 7 27 = 61% Awaria odbiornika 1 6 4 11 25 Awaria innego urządzenia 1 1 1 6 14 Razem (w % okresu) 7,1 5,6 3,3 5,0

By uniknąć gołosłowności przeanalizowano straty (tylko całodzienne) w obserwacjach w ostatnim okresie. Analizą tą, objęto tylko okres po 11 IX 1974 r., gdyż przedtem wystąpiła dłużej trwająca przerwa spowodowana uszkodzeniem systemu antenowego. Rezultaty zawierają tab. 4 i 5. W pierwszej z nich przedstawiono rozkład strat wg dni tygodnia. Dla porównania podano tam analogiczny rozkład w latach 1968–1969. Komentarz wydaje się zbyteczny wobec wymowy liczb, warto jednak dodać, że z 31 dni straconych w niedzielę lub poniedziałek, aż 20 wystąpiło w niedzielę i następujący po niej poniedziałek (po kolei). Jeszcze bardziej przekonywająca wydaje się być tab. 5, w której zawarto podział strat na przyczyny. Podziału dokonano w ten sposób, że przez brak obsługi rozumiano wszelkie usterki systemu odbiorczego, które były możliwe do usunięcia w ramach codziennej obsługi, gdyby tylko zostały w porę zauważone. Do nich wliczono m.in. awarie automatu zegarowego włączającego zapis obserwacji i niesprawności samopisów (brak tuszu, brak taśmy papierowej, uszkodzenie taśmy uniemożliwiające zapis). Awarie odbiornika to długotrwałe niestabilności jego pracy lub wzbudzenie się {występowały głównie w letnie upalne dni). Do innych usterek zaliczono awarie zasilacza stabilizowanego (zasilacz odbiornika), uszkodzenie złącza antena – linie przesyłowe lub brak napięcia w sieci.

Do pozytywów warto dorzucić fakt, że tych straconych obserwacji w ostatnich latach jest jednak nieco mniej (tab. 2), nawet jeśli pominąć w rachunkach przerwy długoczasowe, wynikające z poważniejszych przyczyn. Najczęstszą przyczyną pojedynczych przerw w obserwacjach były niesprawności samopisów, a w tym kontekście wprowadzenie równoległego zapisu na dwóch rejestratorach niewątpliwie wydatnie zmniejszyło procent obserwacji zmarnowanych. Stosowane obecnie rejestratory (LRK-1) ulegają jednak tak częstym usterkom, że nawet ich dublowanie nie gwarantuje uzyskania jednego choćby zapisu z systemu pozostawionego przez 2–3 dni bez opieki. Na ich usprawiedliwienie trzeba dodać, że warunki ich pracy urągają niekiedy podstawowym wymogom klimatycznym. Pewnej dalszej poprawy skuteczności zapisu można oczekiwać w niedalekiej przyszłości, po zainstalowaniu elektronicznego układu włączenia i wyłączania zapisów w miejsce zawodnego zegara mechanicznego. Nie wyeliminuje to, oczywiście, strat poniesionych w wyniku awarii samopisów czy, jak kto woli, braku przynajmniej jednokrotnej w ciągu dnia kontroli przebiegu obserwacji.

7. DODATEK

Antena jest urządzeniem liniowym, dlatego sygnały indukują w niej napięcia proporcjonalne do chwilowych amplitud pola elektrycznego odbieranych fal w składowej o kierunku polaryzacji anteny (płaszczyzna E w przypadku dipola). Uśrednioną po czasie moc wydzielaną na obciążeniu anteny można wyrazić przez średnią kwadratową wartości indukowanego napięcia:

P ~ E[(   ∑ i  Vi + U)2],

(3)

gdzie: E[ ] jest symbolem wartości średniej, ΣV_i oznacza skończoną sumę napięć wywołanych przez sygnały wzajemnie skorelowane, a U — przyczynek od promieniowania niespójnego lub nieskorelowanego z poprzednimi. Występujący w rozwinięciu wyrażenia opisującego uśredniany sygnał iloczyn składników nieskorelowanych znika przy dostatecznie długim uśrednianiu, (3) można więc przepisać do postaci:

P ~ E(∑i,jViVj) + C,

(4)

gdzie: C = E(U²) w radioastronomicznej praktyce oznacza zwykle wolnozmienne tło dla sygnału obserwowanego. Dla dwóch sygnałów wąskowstęgowych zachodzi związek:

E(ViVj) = √   E(V2i)E(V2j)   cos(Ψi – Ψj),

(5)

co się łatwo sprawdza w przypadku, gdy te sygnały są harmoniczne. Jeżeli różnica faz sygnałów Ψ_i – Ψ_j i powstaje jedynie z różnicy τ_ij w czasie przybycia czół fal do środka promieniowania anteny, to jest ona równa 2πfτ_ij, gdzie f jest częstością odbieranych fal. Dla napięć szumowych w skończonej wstędze częstości Δf czynnik fazowy w (5) powinien być zastąpiony pnez odpowiednią średnią po wszystkich częstościach wstęgi, jest to jednak zbyteczne jeśli tylko nierówność:

2πΔfτij = 2π Δf f dij << 1

(6)

jest spełniona dla wszystkich opóźnień odpowiadających różnicom dróg d_ij (C h r i s t i a n s e n, H ö g b o m 1969). Tak np. przy częstości 127 MHz, wstędze 230 kHz i opóźnieniu 10 λ (toruński interferometr) lewa strona (6) wynosi 0,11, co zadowalająco spełnia ten warunek.

Kładąc w (5) E(V²_i) = E²_i z (4) i (5) dostaje się:

P ~ ∑EiEjcosΨicosΨj + ∑EiEjsinΨisinΨj + C.

(7)

Jeżeli do pomiaru sygnału używa się radiometru o charakterystyce kwadratowej, wówczas dostaje się na wyjściu napięcie proporcjonalne do mocy P albo, przepisując inaczej prawą stronę związku (7), do:

V = (∑iEicosΨi)2 + (∑iEisinΨi)2 + C

(8)

— dodać trzeba, że E_j wyraża tutaj skuteczną amplitudę pola elektrycznego i-tej wiązki promieniowania we właściwej składowej polaryzacji pomnożoną przez napięciową charakterystykę promieniowania anteny.

Pożytecznie jest zauważyć, że wzór (8) jest stosunkowo ogólny i łatwo go zastosować do dowolnego zestrojenia anten oraz układu obserwowanych źródeł. Przy obserwacji za pomocą kilku połączonych anten wzór ten pozostaje słuszny po uwzględnieniu w fazach Ψ_i dodatkowych opóźnień powstałych przypadkowo lub celowo w liniach przesyłowych — np. wskutek przełączania fazy w interferometrze typu Ryle'a albo na wyjściu odbiornika interferometru korelacyjnego pojawiają się napięcia postaci (8), w której C znika. Zastosowanie systemu odbiorczego typu Dicke'go zmniejsza tylko wartość „stałej" C o wielkość proporcjonalną do mocy szumów źródła porównawczego. W szczególności, w prostym (dwuantenowym) interferometrze addytywnym skierowanym na punktowe źródło kosmiczne, wyrażenie (8) sprowadza się do:

V = 2E2[1 + cos(Ψ2 – Ψ1)] + C = 4E2cos2 ( Ψ2 – Ψ1 2 ) + C,

(9)

gdzie położono E = E₁ = E₂ sugerując tym identyczność obu anten. Nietrudno też pokazać, wykorzystując dowolność wielkości C, że w przypadku dwóch takich źródeł obserwowanych jednocześnie wyrażenie analogiczne do (9) ma postać:

V = 4E2cos2 ( Ψ2 – Ψ1 2 ) + 4E'2cos2 ( Ψ'2 – Ψ'1 2 ) + C,

(10)

gdzie primami odróżniono amplitudy i fazy sygnałów z drugiego źródła. Wzór (10) daje pożyteczną podstawę do oceny zakłóceń obserwacji wywołanych obecnością niezbyt odległych kątowo źródeł (ważny problem toruńskich kalibracji obserwacji Słońca na źródłach Cas A i Cyg A).

Do opisu faz sygnałów konieczna jest znajomość rozmieszczenia anten. Pouczająca będzie analiza prostego przypadku z dwoma antenami. Jeśli w środku układu kartezjańskiego o osiach skierowanych na zachód (x), na południe (y) i na północy biegun nieba (z) mieści się jedna z anten, a druga ma współrzędne x_o, y_o i z_o, to transformują się one ze współrzędnych równikowych przez przekształcenie:

xo = d cosδosin to yo = d cosδocos to zo = d sinδo

(11)

gdzie: d = √(x_o² + y_o² + z_o²) jest odległością między antenami, a δ_o i t_o są deklinacją i kątem godzinnym kierunku wyznaczonego przez anteny. Różnica dróg przebytych przez czoło fali biegnącej do anten z kierunku o współrzędnych δ i t jest rzutem wektora przypisanego bazie interferometru d(x_o,y_o,z_o) na ten kierunek, czyli:

d·1(cosδsin t,cosδcos t,sinδ) = d(cosδcosδosin t sin to + cosδcosδocos t cos to + sinδsinδo),

gdzie 1(...) jest wektorem jednostkowym w kierunku źródła osadzonym w początku układów współrzędnych. Ta różnica dróg jest miarą różnicy faz (wyrażonej w radianach):

Ψ2 – Ψ1 = 2πd[cosδcosδocos(t – to) + sinδsinδo].

(12)

Bardzo często interferometry buduje się tak, by baza leżała na linii wschód–zachód i zawsze wymagana jest znajomość odchyłek od tego położenia. Korzystając z wzoru (12) nietrudno zauważyć, że różnica fazy sygnału źródła obserwowanego interferometrem rzeczywistym (11) i interferometrem o bazie d_o ustawionym idealnie na osi x wyniesie:

Ψ2 – Ψ1 – 2πdocosδsin t = 2π{[(xo – do)sin t + yocos t]cosδ – zosinδ},

(13)

gdzie x_o – d_o, y_o i z_o są dodatnimi odchyłkami (w λ) bazy odpowiednio: w kierunku zachodu, południa i ponad płaszczyznę równika niebieskiego. W praktyce właśnie z tej zależności korzysta się przy wyznaczaniu odchyłek w podanych kierunkach (E l s m o r e i in. 1966).

W rzeczywistości oprócz różnicy faz wynikającej z usytuowania anten powstaje zwykle też przesunięcie na skutek różnicy w długościach linii przesyłowych D (w λ) do punktu węzłowego, które trzeba dołączyć do różnicy (12). W przypadku, gdy δ = 0° i t_o = 90° (anteny na osi x) wzór (9) przechodzi w:

V = 2E2{1 + cos[2π(d cosδsin t + D)]} + C,

lub, zaniedbując stałe, w:

V ~ cos[2π(d cosδsin t + D)].

(14)

Autor pragnie dodać, iż powyższa praca powstała w znaczącym stopniu dzięki bezinteresownej pomocy wielu osób — pracowników Obserwatorium. Szczególne wyrazy wdzięczności chce on przekazać Dr. J. H a n a s z o w i  za nieustanną pomoc w wielu problemach związanych z obserwacjami Słońca, Dr. A. W o l s z c z a n o w i  za wprowadzenie w arkana dyskretnej analizy widmowej i Mgr inż. J. U s o w i c z o w i  za dyskusje z teorii sygnałów oraz życzliwie udostępnienie własnych zbiorów literaturowych.

LITERATURA

B e n d a t, J.S., P i e r s o l, A.G., 1976, Metody analizy i pomiaru sygnałów losowych, PWN , Warszawa.

B o r k o w s k i, K.M., 1975, Post. Astr., 23, 199.

B o r k o w s k i, K.M., 1976a, Post. Astr., 24, 15.

B o r k o w s k i, K.M., 1976b, Post. Astr., 24, 115.

B o r k o w s k i; K.M., G o r g o l e w s k i, S., U s o w i c z, J., 1975, Post. Astr., 23, 141.

B o r k o w s k i, K.M., K ę p a, A., 1976, Urania, 47, 89.

B r o w n, J.S., 1974, 1975, informacje prywatne.

C h r i s t i a n s e n, W.N., H ö g b o m, J.A., 1969, Radiotelescopes, Cambridge University Press, Cambridge.

C o c h r a n, W.T., C o o l e y, J.W., F a v i n, D.L. i inni, 1967, IEEE Trans. Audio Electroacoust., 15, 45, No 2.

C o l e, T.W., 1973, Solar Physics, 30, 103.

Complete Summary of Daily Solar Radio Flux, Series-70, Toyokawa 1975.

C o v i n g t o n, A.E., 1974, J. R. Astr. Soc. Can., 68, 31.

C o v i n g t o n, A.E., 1976, SGD, No. 378 (Supplement), 8.

C u r r i e, R.G., 1973, Astrophys. Space Sci., 20, 509.

D e n t, W.A., A l l e r, H.D., O l s e n, E.T., 1974, Astrophys. J., 188, L11.

E l- R a e y, M., A m e r, R., 1975, Solar Physics, 45, 533. .

E l s m o r e, B., K e n d e r d i n e, S., R y l e, M., 1966, MNRAS, 134, 87.

E r i c k s o n, W.C., P e r l e y, R.A., 1975, Astrophys. J., 200, 183.

G a w r o ń s k a, G., 1977, praca magisterska UMK.

K a n d a, M., 1976, IEEE Trans. Instr. Measur., 25, 173,

MONSEE Bulletin No.8, p. 10, ICSU Special Committee on Solar-Terrestrial Physics., Sep. 1976.

P i c q u e n a r d, A., 1974, Radio Wawe Propagation, Macmillan, London and Basingstoke.

Quarterly Bulletin on Solar Activity, 1959–1976, IAU, Zürich.

R e a d, P.L., 1976, 9th Young European Radio Astronomers Conference (YERAC), 2–5 Aug., Toruń. oraz MNRAS, 178, 259 (1977).

S c h w a r t z, M., S h a w, L., 1975, Signal Processing, McGraw-Hill, N. York.

S o b k o w s k i, J.. 1975, Częstotliwościowa analiza sygnałów, Wyd. MON, Warszawa.

Solar-Geophysical Data (SGD), 1975–1977, U.S. Department of Commerce, Boulder, Colorado.

Solar-Terrestrial Physics and Meteorology: A Working Document, SCOSTEP Secretariat, July 1975, Washington.

S z y m a ń s k i, W., 1976, Urania, 47, 88.

T s e y t l i n, N.M., D m i t r i e n k o, L.V., D m i t r i e n k o, D.A., M i l l e r, E.A., S n e g i r e v a, V.V., T i t o v, G.K., 1976, Radiofizika, XIX, 1106.

U l r y c h, T.J., 1972, J. Geophys. Res., 77, 1396.

Urania, 1975–1977, PTMA, Kraków,

W h i t f i e l d, G.R., 1959, Paris Symposium on Radio Astronomy (Ed. R.N. Bracewell), p. 297, Stanford, California.

W i e l e b i n s k i, R., 1976, Methods of Experimental Phys. (Astrophys.), 12, 82.