POSTĘPY  ASTRONOMII
Tom XXVIII (1980), Zeszyt 2, 79–93

TEORIA  ODBIORU INTERFEROMETRYCZNEGO W  RADIOASTRONOMII

THEORY OF THE INTERFEROMETER IN RADIO ASTRONOMY Summary     A theory of interferometric measurements is presented with special emphasis put upon solar observations made with a short baseline system. Interesting result of discussion is the response of the interferometer with a Gaussian frequency band to a source with Gaussian brightness distribution and response of the simple interferometer to a many-point source. A theoretical background for main interferometer parameters determination based on phase measurements is presented. Finally, the simple interferometer theory is broadened to a many-element interferometer.

1. WSTĘP

Podstawowymi obserwablami w radiointerferometrii są skorelowane amplitudy i względne fazy fal pochodzących ze wspólnego źródła w dwóch punktach przestrzeni. Wektor łączący takie dwa punkty zwany jest bazą interferometru. Zasady działania interferometrów radiowych są takie same, jak interferometrów optycznych. Użycie na tych falach technik interferometrycznych, albo korelacyjnych, jest więc logicznym rozszerzeniem praktyk optycznych zapoczątkowanych przez M i c h e l s o n a. W rzeczywistości wiele radioteleskopów jest przeskalowaną wersją odpowiedników optycznych. Są jednak także wyjątki, w których nowe techniki korelacyjne opracowane przez radioastronomów przyczyniły się do postępu obu gałęzi (np. R y l e 1952).

Mimo stosunkowo niedługiego „stażu" radiointerferometrii obecnie istnieje już wiele dobrze opracowanych teorii, uwzględniających szczególne wymagania narzucane przez praktyczne zastosowania. Inne zagadnienia teoretyczne są ważne w zastosowaniu do interferometrii bardzo wielkich baz (C a n n o n 1978), a inne do syntezy apertury (B r o u w 1968; R o g e r s 1976; C o l e 1979). Jeszcze inne elementy okazują się istotne w obserwacjach z małymi bazami, spotykanymi w służbach Słońca. Te ostatnie będę starał się uwypuklić w niniejszej pracy. Wypada jeszcze podkreślić, że prawie wszystkie teorie interferometrów opierają się na podstawach wypracowanych w optyce (B o r n i W o l f 1964). Stamtąd też pochodzi znaczna część terminów i pojęć w rodzaju: tensor (K o 1967) i funkcja spójności czy funkcja widzialności.

Pole elektromagnetyczne badane przez radioastronoma fluktuuje bardzo szybko i nieregularnie w czasie. Pola takie nazywa się statystycznymi. Wcześniejsze teoretyczne analizy interferometrów przeprowadzano przy założeniu, że odbierane promieniowanie jest monochromatyczne lub prawie monochromatyczne. Mimo tak jawnego odstępstwa założeń od rzeczywistości dawały one zadawalające rezultaty w wielu problemach praktycznych (C a r t e r i S o m e r s 1976). Wstępnie przyjmuje się zawsze, że mierzony sygnał jest ergodycznym, gaussowskim procesem losowym (o zerowej średniej), który jest stacjonarny zarówno w domenie czasu jak i przestrzeni. Chociaż w praktyce to założenie nigdy nie jest spełnione, to jednak odchylenia przewidywań teoretycznych od wyników doświadczalnych są w bardzo wielu przypadkach zaniedbywalnie małe. Praktycznie też zawsze używa się pojęcia sygnału analitycznego, który jest pewną konstrukcją pozwalającą wygodnie prezentować zachowanie się instrumentów pobudzonych sygnałem rzeczywistym. Ten ostatni jest częścią rzeczywistą owego sygnału analitycznego, zaś jego część urojona jest transformatą Hilberta sygnału rzeczywistego i ma te same charakterystyki statystyczne, co sygnał oryginalny, ale mimo to nie jest z nim skorelowana. Szczegółową dyskusję konstrukcji i własności sygnału analitycznego można znaleźć w wielu książkach (przejrzyste przedstawienia podano np. u K n o c h a i E k i e r t a 1979; B r a c e w e l l a 1965 czy też S w i e s z n i k o w a 1965).

W dalszych punktach pracy przedstawię szkic teorii interferometru i kilka zastosowań praktycznych, wybranych z myślą o obserwacjach Słońca na falach metrowych. Z tego powodu przedstawienie to nie pretenduje ani do przymiotu „kompletne", ani „ogólne". Chociaż oparte na ideach zawartych w pracy S w e n s o n a i M a t h u r a (1968), jest ono prawie w całości jednolitym i oryginalnym opisem wszystkich istotnych zagadnień, z którymi zetknąłem się w praktyce obserwacyjnej. Dostępna literatura nie zawiera spójnych opisów tak ważnych zagadnień, jak detekcja „niekwadratowa", dudnienia, odbicia itp. w zastosowaniu do obserwacji interferometrycznych.

Wszystkie całki występujące w tej pracy są całkami oznaczonymi. Jeżeli symbol całkowania nie ma wskazanych granic, trzeba rozumieć, że całkowanie odbywa się na całej współrzędnej (–∞,+∞).

2. TEORIA PROSTEGO INTERFEROMETRU ADDYTYWNEGO

Niech E(ξ,t) oznacza kątowy rozkład pola elektrycznego promieniowania odbieranego ze źródła „stacjonarnego" w funkcji czasu t, gdzie ξ = sinθ jest cosinusem kierunkowym źródła (cosinusem kąta między kierunkiem na źródło i kierunkiem bieguna bazy; θ jest dopełnieniem tego kąta do 90°, rys. 1). W i-tej antenie indukuje się napięcie proporcjonalne do:

v(ξi,fi) = ∫ Ě(ξ',fi)Gi(ξ' – ξi) dξ',

(1)

gdzie G_i(ξ_i,f_i) jest kierunkową charakterystyką napięciową promieniowania i-tej anteny w funkcji częstości f_i, a Ě jest transformatą Fouriera rozkładu E (Ě = ∫E exp(–i2πft) dt). Po wzmocnieniu i odfiltrowaniu przez wzmacniacze w.cz. o napięciowej charakterystyce przenoszenia A_i(f_i), sygnały wyjściowe można przedstawić w postaci:

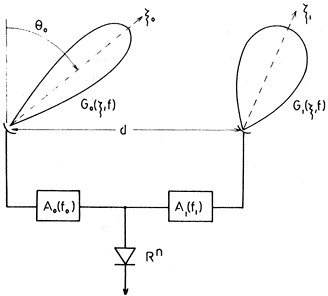Rys. 1. Schemat interferometru dwuantenowego

Vˇ(ξi,fi)  = v(ξ,fi)Ai(fi) = ∫ Ě(ξ,fi)Gi(ξ – ξi,fi)Ai(fi) dξ.

(2)

Moc sumy dwóch sygnałów postaci (2) wynosi:

lim T→∞ 1 2T ∫ |VT(ξo,t) + VT(ξ1,t – τ)|2dt ≡ <|V(ξo,t) + V(ξ1,t – τ)|2 >,

(3)

gdzie wskaźnik T oznacza napięcie typu (2), ale wywołane przez sygnał analityczny E_T(ξ,t), skonstruowany z rzeczywistego przyrównanego do zera dla |t| > T, a znak ≡ użyłem dla zdefiniowania innego sposobu zapisu. Wyżej określone obcięcie sygnału rzeczywistego pozwala zrealizować całkowanie sygnału stacjonarnego i wykonywać analizę fourierowską. Sygnały V^ˇ i V wiąże przekształcenie Fouriera, analogicznie do wielkości Ě i E.

Na tym etapie dostępne opracowania teorii interferometrów zakładały, że następnym stopniem przetwarzania sygnału jest detektor kwadratowy, na którego wyjściu pojawia się napięcie proporcjonalne do kwadratu napięcia wejściowego, a zatem do chwilowej mocy sygnału. Gdzie indziej (B o r k o w s k i 1980) pokazałem, że jeżeli do wejścia detektora obwiedni (chwilowej amplitudy) R o charakterystyce Rⁿ, gdzie n jest rzeczywiste i dodatnie, przyłożyć napięcie losowe o rozkładzie prawdopodobieństwa obwiedni typu Rayleigha (wąskopasmowy szum gaussowski), to na wyjściu otrzyma się napięcie, którego wartość średnia jest proporcjonalna do <R²>^n/2. Uśredniając zatem napięcie wyjściowe uogólnionego w powyższy sposób detektora, dostaje się w miejsce wyrażenia (3) wielkość proporcjonalną do:

V(ξo,ξ1,τ) ≡ <|V(ξo,t) + V(ξ1,t – τ)|2>n/2 = = [<|V(ξo,t)|2> + <|V(ξ1,t – τ)|2> + 2·Re <V(ξo,t)V*(ξ1,t – τ)>]n/2,

(4)

gdzie Re oznacza część rzeczywistą, a symbol * (gwiazdka) — wartość sprzężoną. Korzystając teraz ze związków (1), (2) i (3) oraz jednej z reprezentacji dystrybucji delta Diraca (δ(f₁ – f_o) = ∫exp[–i2π(f₁ – f_o)t] dt) nietrudno już pokazać, że:

<V(ξo,t)V*(ξ1,t – τ)> =

= ∫∫∫ Γ(ξ'o,ξ'1,f)Ao(f)A*1(f)Go(ξ'o – ξo,f)G*1(ξ'1 – ξ1,f)ei2πfτ df dξ'odξ'1,

(5)

gdzie:

Γ(ξo,ξ1,f) =  lim T→∞ ĚT(ξo,f)Ě*T(ξ1,f)

(6)

jest tzw. funkcją spójności wzajemnej.

Warto zauważyć, że związek (5) określa zależność napięcia (prądu) wyjściowego interferometru korelacyjnego (tzn. takiego, w którym sygnały z obu anten nie są dodawane, lecz wymnażane w urządzeniu spełniającym rolę detektora kwadratowego) od funkcji spójności wzajemnej źródła polichromatycznego i częściowo spójnego oraz od charakterystyk promieniowania anten i charakterystyk filtrów (S w e n s o n i M a t h u r 1968).

Ponieważ promieniowania pochodzące z dwóch różnych punktów źródła są statystycznie niezależne (źródło całkowicie niespójne), co można formalnie zapisać w postaci równości:

Γ(ξo,ξ1,f) = Γ(ξo,f)δ(ξo – ξ1),

zatem całkę występującą w (5) można uprościć, przez scałkowanie po jednym z kierunków, do:

<V(ξo,t)V*(ξ1,t – τ)> = ∫∫ Γ(ξ,f)Ao(f)A*1(f)Go(ξ – ξo,f)G*1(ξ – ξ1,f)ei2πfτ df dξ,

(7)

i, jako szczególnego przypadku tego związku,

<|V(ξ1,t – τ)|2> = ∫∫ Γ(ξ,f)|A1(f)|2|G1(ξ – ξ1,f)|2df dξ,

(8)

oraz analogicznego do tego wyrażenia na <|V(ξ_o,t)|²>.

Wzory (4), (7) i (8) opisują zależność napięcia (prądu) wyjściowego w interferometrze addytywnym od funkcji spójności źródła całkowicie niespójnego.

Dalszą dyskusję przeprowadzę przy założeniu identyczności obu gałęzi interferometru i jednakowej orientacji anten (poprzez opuszczenie wskaźników 0 i 1 przy A i G) oraz przy zaniedbaniu zmian charakterystyki anten i funkcji Γ na skończonym przedziale Δf częstości filtrów (A). Założenia te pozwalają przepisać wzory (7) i (8) w prostszej postaci:

<V(ξo,t)V*(ξ1,t – τ)> =

= ∫ Γ(ξ,fo)|G(ξ – ξo,fo)|2 ∫ fo+Δf/2 fo–Δf/2  |A(f)|2ei2π(f + fo)τd(f + fo)·dξ =

= ∫ Γ(ξ,fo)|G(ξ – ξo,fo)|2ei2πfoτ ∫ Δf/2 –Δf/2  |A'(f)|2exp(i2πfτ) df dξ

(9)

oraz

<|V(ξo,t)|2> = <|V(ξo,t – τ)|2> =

= ∫ Γ(ξ,fo)|G(ξ – ξo,fo)|2 ∫ fo+Δf/2 fo–Δf/2  |A(f)|2df dξ =

= ∫ |A(f)|2df· ∫ Γ(ξ,fo)|G(ξ – ξo,fo)|2dξ

(10)

gdzie A'(f) = A(f – f_o).

Użycie tych zależności we wzorze (4) upraszcza go do:

V(ξo,ξo,τ) ≡ V(ξo,τ) = [2 ∫ |A(f)|2df· ∫ Γ(ξ,fo)|G(ξ – ξo,fo)|2dξ

+ 2Re ∫ Γ(ξ,fo)|G(ξ – ξo,fo)|2ei2πfoτ ∫ |A'(f)|2exp(i2πfτ) df dξ]n/2.

(11)

Wyrażenie (11), mimo swej stosunkowo dużej ogólności, jest już wygodnym punktem startowym do praktycznych problemów obserwacyjnych. W dalszym ciągu będą mi potrzebne tylko przypadki, w których charakterystyka |A(f)|² jest symetryczna względem częstości środkowej f_o, a funkcje spójności są rzeczywiste. Warto zauważyć, że i te ograniczenia praktycznie niewiele ujmują z ogólności wyrażenia (11), które teraz sprowadza się do postaci:

V2/n(ξo,τ) ~ ∫ Γ(ξ,fo)|G(ξ – ξo,fo)|2dξ +

+ ∫ Γ(ξ,fo)cos(2πfoτ)|G(ξ – ξo,fo)|2 ∫ |a(f)|2cos(2πfτ) df dξ,

(12)

gdzie |a(f)|² = |A'(f)|² / ∫|A(f)|²df.

3. TRZY PRZYKŁADY

W przypadku obserwacji skończonej liczby źródeł punktowych, znajdujących się jednocześnie w obrębie charakterystyki anten, funkcję spójności można przedstawić w postaci:

Γ(ξ,f) = Σ i  Si·δ(ξ – ξi).

(13)

Scałkowanie prawej strony związku (12) daje w tym przypadku wprost opis sygnału wyjściowego interferometru z detekcją kwadratową:

Σ i  SiG(ξ – ξo,fo)|2 [ 1 + ∫ |a(f)|2cos(2πfτi) df·cos(2πfoτi) ] .

(14)

Jeżeli wstęga Δf jest dostatecznie wąska (na tyle, by można było położyć: sin(πΔfτ_i) ≈ πΔfτ_i), to ostatnie wyrażenie uprości się dalej i ostatecznie do:

Σ i  SiG(ξ – ξo,fo)|2cos2(πfoτi).

(15)

Taką postać sygnału wyjściowego przyjąłem na podstawę do oceny zakłóceń kalibracji systemu odbiorczego na częstość 127 MHz na radioźródłach Cas A i Cyg A (B o r k o w s k i 1979).

Pouczające jest również przestudiowanie odpowiedzi interferometru na źródła rozciągłe. Rozpatrzę tutaj dwa przypadki: źródło o gaussowskim rozkładzie jasności i interferometr z gaussowskim kształtem pasma przenoszonych częstości oraz źródło prostokątne i prostokątna wstęga odbiornika.

Niech będą dane źródło i wstęga takie, że:

Γ(ξ,fo) =  S σi exp [ –π  (ξ – ξo)2 σξ2 ]     i

(16a)

|A(f)|2 = exp [ –π  (f – fo)2 σf2 ] .

(16b)

Warto odnotować, że z powyższych określeń wynika, że ∫Γdξ = S oraz ∫|A(f)|²df = σ_f i że szerokości krzywych (wyznaczone przez σ_ξ i σ_f) opisanych wzorami (16) są bardzo bliskie szerokościom połówkowym lub 3-decybelowym.

W tym szczególnym przypadku odpowiedź systemu odbiorczego można wyznaczyć ściślej, bez uciekania się do uproszczenia (12). Zakładając, że funkcja G jest wolnozmienna w porównaniu z Γ, odpowiedź tę można uzyskać z wyrażeń typu (7) i (8), w których opuszczono wskaźniki 0 i 1 przy G i A. Nieco kłopotliwe, ale ścisłe przekształcenia prowadzą do rezultatu:

V2/n(ξo,τ) ~ 1 + W(σξ,σf) cos  2πd(ξo + D/d) 1 + (dσξσf/fo)2 ,

(17)

gdzie

W(σξ,σf) = [ 1 + ( dσξ  σf fo ) 2   ] –1/2   exp {  –πd2 1 + (dσξσf/fo)2 [ ( ξo +  D d ) 2    σf2 fo2 + σξ ] }

(18)

jest funkcją widzialności, a d — bazą interferometru wyrażoną w długościach fali λ = c/f_o, gdzie c oznacza prędkość światła). Przy wyprowadzeniu wzorów (17) i (18) przyjąłem ponadto, że:

foτ = D + ξod,

(19)

gdzie D jest zapóźnieniem instrumentalnym wyrażonym w długościach fali.

Jeżeli źródło i pasmo przepuszczania mają charakterystyki prostokątne, to:

Γ(ξ,fo) = S/Δξ, gdy |ξ – ξo| ≤ Δξ/2 0, gdzie indziej,

(20a)

∫ |a(f)|2cos(2πfτ) df = sin [ π  Δf fo (D + ξod) ] π  Δf fo (D + ξod)

(20b)

Utrzymując w mocy założenie o małości Δξ względem szerokości charakterystyki |G|² i dołączając warunek, by Δf << f_o, ze związków (12) i (20) uzyskuje się stosunkowo prosto proporcjonalność:

V2/n(ξo,τ) ~ 1 + W(Δξ,Δf) cos[2π(D + ξod)],

(21)

gdzie

W(Δξ,Δf) =  sin(πdΔξ) πdΔξ sin [ πd  Δf fo (  D d + ξo  )  ] πd  Δf fo (  D d + ξo  )

(22)

jest znów funkcją widzialności. Widzialność listków interferencyjnych (odpowiednik prążków optycznych) definiuje się jako stosunek ich amplitudy (amplitudy przebiegów sinusoidalnych wyznaczonych np. przez wzory (17) i (21)) do całkowitego strumienia źródła. Wzór (22) będzie w zgodzie z odpowiednikami spotykanymi w literaturze, jeśli ξ_o potraktować jako małe (tzn. przyjąć, że ξ_o = sinθ_o ≈ θ_o) i zaniedbać D. Uprości się on wtedy do:

W(Δξ,Δf) =  sin(πdΔθ) πdΔθ  sin(πξodΔf/fo) πξodΔf/fo ,

(23)

gdzie przyjąłem też, że Δξ ≈ Δθ (por. E s e p k i n a i in. 1973).

Porównanie widzialności (18) i (22) nie sugeruje żadnego podobieństwa. W rzeczywistości okazuje się, że dla małych σ_ξ i σ_f (Δξ i Δf) są one niemal równoważne. W przypadku granicznym, gdy te parametry zmierzają do zera, obie funkcje stają się identyczne i równe jedności, czego należało oczekiwać. Warto jeszcze przypomnieć, że wzór (22) jest ograniczony do przypadków, kiedy Δf << f_o, którego to zastrzeżenia nie było przy wyprowadzaniu wzoru (18).

W przytoczonych trzech przykładach skorzystałam z faktu, że funkcja spójności źródła jest po prostu jego rozkładem jasności (albo: rozkładem temperatury jasnościowej).

4. FUNKCJA WIDZIALNOŚCI

Opierając się na podstawach teoretycznych, dopiero co przedstawionych, wyprowadzę teraz wzór na funkcję widzialności w postaci ogólniejszej niż dotychczas dyskutowane. Charakterystyka detektora, jak nietrudno zauważyć na przykładach poprzedniego punktu, nie jest istotna przy rozpatrywaniu widzialności źródła, dlatego mając na uwadze przejrzystość przyjmę dalej, że jest ona kwadratowa (n = 2).

Przy obserwacji pojedynczego, niezbyt dużego w porównaniu z charakterystyką systemu antenowego źródła rozciągłego, sygnał wyjściowy instrumentu odbiorczego będzie proporcjonalny do V(ξ_o,τ) ze wzoru (12), a zatem także do:

1 + ∫ γ(ξ)cos[2π(D + ξd)] ∫ |a(f)|2cos[2π f fo (D + ξd)]df·dξ,

(24)

gdzie γ(ξ) = Γ(ξ,f_o) / ∫Γ(ξ,f_o)dξ.

Ważne są ograniczenia na stosowalność wyrażenia (24). Przypomnę, że przy jego wyprowadzaniu założyłem: 1) sygnał ergodyczny i stacjonarny z całkowicie niespójnego źródła, 2) identyczność obu gałęzi interferometru (w sensie jednakowych charakterystyk kierunkowych, orientacji, wzmocnienia i pasma przenoszonych częstości), 3) słabą zależność funkcji Γ i G od częstości, 4) symetrię filtracji w.cz. względem częstości środkowej f_o oraz 5) rzeczywistość funkcji spójności i małą jej szerokość w porównaniu z szerokością funkcji G.

Zawsze można dobrać takie ξ_o (równoważny w tym sensie kierunek na środek źródła), żeby całka podwójna:

∫ γ(ξ)cos[2π(D + ξd)] ∫ |a(f)|2cos[2π f fo (D + ξd)]df·dξ

znikała. Oznacza to, że całkę występującą w wyrażeniu (24) można przekształcić (rozbijając wyraz D/d + ξ na D/d + ξ_o i ξ – ξ_o) do postaci:

cos[2π(D + ξod)] ∫ γ(ξ)cos[2πd(ξ – ξo)] ∫ |a(f)|2cos[2π f fo (D + ξd)]df·dξ,

(25)

gdzie już łatwo widzieć funkcję widzialności:

∫ γ(ξ)cos[2πd(ξ – ξo)] ∫ |a(f)|2cos[2π f fo (D + ξd)]df·dξ.

(26)

Tę widzialność można wyrazić w wielkościach bardziej czytelnych pamiętając, że ξ = sinθ:

W = ∫ γ'(θ)cosθcos(2πd sinθ) ∫ |a(f)|2cos[2π f fo d(  D d + sinθ + sinθo)]df·dθ,

(27)

gdzie γ'(θ) = γ(sinθ + sinθ_o).

Jeżeli |a(f)|² jest prostokątem w przedziale [–Δf/2,+Δf/2], to wzór (27) zapisuje się prościej:

W = ∫ γ'(θ)cosθcos(2πd sinθ) sin [ πd Δf fo ( D d + sinθ + sinθo ) ] πd Δf fo ( D d + sinθ + sinθo ) dθ.

(28)

W przypadku, gdy Δf/f_o jest małe i małe jest Δθ (a zatem i θ), wzór (28) sprowadza się do postaci znanej z literatury (np. K r a u s 1966):

W = ∫ +Δθ/2 –Δθ/2  γ'(θ)cos(2πd sinθ)dθ.

(29)

Wyrażenia (27) i (25) pozwalają teraz sygnał wyjściowy interferometru addytywnego (24) przedstawić w znacznie przejrzystszej i dobrze znanej formie:

1 + W·cos[2π(D + d·sinθ)].

(30)

W praktyce radioźródła są zawsze obserwowane na tle źródeł bardziej rozciągłych (np. na tle galaktycznym), które mają funkcje widzialności bliskie lub równe zeru. Powoduje to, że wyrażenie (30) należy zwiększyć o składnik słabo zależny od kąta θ.

Wzory (28) i (29) wykorzystałem (B o r k o w s k i 1979) do obliczenia widzialności Słońca dla przypadku interferometru toruńskiego. Okazało się, że widzialność ta jest o ok. 2% mniejsza od jedności. Wcześniejsze, mniej dokładne, oceny wskazywały, że widzialność jest nieco lepsza: więcej niż 0,986 (B o r k ow s k i 1976) i 0,99 (S o l e c k i 1974).

5. PRZEJŚCIE DO UKŁADU WSPÓŁRZĘDNYCH ASTRONOMICZNYCH I KARTEZJAŃSKICH

Kąt θ, który występował w dotychczasowych wzorach, jest mierzony od płaszczyzny prostopadłej do linii bazy interferometru. Jeśli biegun interferometru (jeden z dwóch punktów na sferze niebieskiej wyznaczonych przez kierunek bazy; przyjmuje się nań punkt bliższy północnego bieguna niebieskiego) ma współrzędne równikowe t_o i δ_o (kąt godzinny i deklinacja, odpowiednio), to każdemu punktowi sfery niebieskiej (t,δ) można przypisać kąt θ, korzystając ze znanych zależności trygonometrii sferycznej. Zachodzi mianowicie:

sinθ = sinδosinδ + cosδocosδcos(to – t).

(31)

Jeśli współrzędne bieguna interferometru podane są w układzie horyzontalnym: A_o i h_o (azymut i wysokość, odpowiednio) i w tym samym układzie współrzędne źródła (A,h), to odpowiednia do (31) relacja przyjmuje postać:

sinθ = sin hosin h + cos hocos h cos(Ao – A).

(32)

Warto zauważyć, że d·sinθ, występujące we wzorze (30), można wyrazić, w ogólności, w dowolnych współrzędnych korzystając z faktu, że:

d·sinθ = d·1,

(33)

gdzie d jest wektorem o długości bazy i kierunku wyżej zdefiniowanego bieguna interferometru, zaś 1 jest wersorem o kierunku źródła promieniowania.

Łatwo jest zauważyć, że jeśli początek układu kartezjańskiego (współrzędnych prostokątnych) umieści się w ognisku anteny leżącej bliżej punktu wschodu i oś x skieruje na zachód, y — na południe (w płaszczyźnie równika niebieskiego), a z — na północny biegun nieba, to współrzędne drugiej anteny (x_o,y_o,z_o) można znaleźć z przekształcenia:

xo = d cosδosin to yo = d cosδocos to zo = d sinδo .

(34)

6. WYZNACZANIE PARAMETRÓW INTERFEROMETRU I EKSTREMÓW INTERFERENCYJNYCH

Fazę sygnału wyjściowego interferometru opisuje argument cosinusa w wyrażeniu (30). Rozwinięcie sinθ w tym argumencie zgodnie z wzorem (31) daje na fazę wartość (w cyklach):

Ψ/(2π) = D + d(sinδosinδ + cosδocos tocosδcos t + cosδosin tocosδsin t).

(35)

W tym wyrażeniu łatwo jest wyróżnić prawe strony przekształcenia (34), co pozwala na dalsze jego uproszczenie do postaci:

Ψ/(2π) = D + xocosδsin t + yocosδcos t + zosinδ.

(36)

Z tego wzoru widać, że pomiar fazy Ψ dla kilku punktów (t,δ) pozwala wyznaczyć parametry D, x_o, y_o i z_o (wszystkie wyrażone w długościach fali). Przekształcenie odwrotne do (34) może służyć do odzyskania parametrów d, t_o i δ_o.

Zwrócę uwagę na pewną modyfikację wzoru (36), wykorzystywaną niekiedy w praktyce do badania interferometrów o bazie leżącej blisko kierunku wschód-zachód. Ponieważ instrumentalne przesunięcie fazy D można dokładniej wyznaczyć z innego rodzaju pomiarów, przyjmę dalej, że jest ono znane.

Gdyby baza d' leżała idealnie na osi x (wschód-zachód), wówczas faza sygnału wyjściowego takiego instrumentu, jako szczególny przypadek wzorów (35) lub (36), wyniosłaby:

Ψ' = 2π(D + d'cosδsin t).

Odchyłka fazy interferometru rzeczywistego od założonego w powyższym wyrażeniu wynosi zatem Ψ – Ψ', tzn.:

2π{[(xo – d')sin t + yocos t]cosδ + zosinδ},

(37)

co jest w zgodzie z wyrażeniem przedstawionym (bez wyprowadzenia) przez E l s m o r e'a i in. (1966).

W przypadku interferometrów o krótkich bazach, ze względu na powolność zmiany fazy z kątem godzinnym t, dokładność wyznaczenia bazy i jej przestrzennej orientacji jest stosunkowo mała. Dokładniejsze wyniki uzyskuje się z pomiarów geodezyjnych.

Ze wzoru (30) wynika, że sygnał wyjściowy interferometru ma przebieg sinusoidalny z ekstremami dla momentów, kiedy:

D + d[sinδosinδ' + cosδocosδ'cos(to – t'k)] = k/2,

(38)

gazie k = ..., –1,0,1, ..., a primami zaznaczyłem współrzędne obserwowane (widome z miejsca obserwacji) źródła. Gdy k przyjmuje wartości parzyste, to ekstrema są maksimami.

Przekształcając odpowiednio wzór (38), można wyznaczyć kąt godzinny, przy którym pojawi się ekstremum interferencyjne:

t'k = to – arccos ( k – 2D 2d cosδocosδ' – tgδotgδ' ) .

(39)

W przypadku instrumentu umieszczonego pod atmosferą Ziemi zarówno kąt godzinny t'_k jak i deklinacja δ', występujące we wzorach (38) i (39), są skażone refrakcją. Z tego powodu nie można tych wzorów użyć wprost do nawiązania czasowego przebiegu fazy. Zjawisko refrakcji powoduje wzrost rzeczywistej wysokości źródeł kosmicznych o wartość R zależną od wysokości h źródła nad horyzontem. Efekt tego zjawiska jest taki sam, jak gdyby kąt godzinny i deklinacja źródła były zwiększone (por. np. K u l i k o v 1961) odpowiednio o:

Δt = –R cosφsin tk / (cos h cosδ)     i Δδ = R cos h (cosδsinφ – sinδcosφcos tk),

(40)

gdzie h = arcsin(sinδsinφ + cosδcosφcos t_k), a φ jest szerokością geograficzną miejsca obserwacji. Uwzględnienie w (39) poprawek (40) pozwala napisać:

tk = to – arccos [  k – 2D 2d cosδocos(δ + Δδ) – tgδotg(δ + Δδ) ] – Δt.

(41)

Kąt godzinny t_k, wyliczony przy pomocy wzoru (41) można teraz powiązać z czasem gwiazdowym lub słonecznym średnim:

Sk = tk + α   lub mk = tk + 12h – η,

(42)

odpowiednio, gdzie α jest rektascensją źródła, a η — równaniem czasu (czas prawdziwy minus czas średni).

7. INTERFEROMETR ZŁOŻONY A ODBICIA OD ZIEMI

Przedstawiona wcześniej teoria dotyczyła interferometru dwuantenowego. W przypadku, gdy interferometr składa się z wielu anten, z których sygnały sumuje się przed detekcją, uśredniony sygnał podetekcyjny opisuje zależność ogólniejsza:

V(ξ1,ξ2,...,ξN,τ1,τ2,...,τN) = < N |Σ   k=1 V(ξk,t – τk) |2 >n/2  =

= [ Re Σ k,l <V(ξk,t – τk)V*(ξl,t – τl)> ] n/2   ,

(43)

której przypadek szczególny, gdy N = 2, pokrywa się ze wzorem (4).

Dla źródła całkowicie niespójnego wyrażenie analogiczne do (7) przyjmuje teraz postać:

<V(ξk,t – τk)V*(ξl,t – τl)> =

= ∫∫ Γ(ξ,f)Ak(f)A*l(f)Gk(ξ – ξk,f)G*l(ξ – ξl,f)ei2πf(τl – τk) df dξ.

(44)

Oryginalny i elegancki opis sygnału wyjściowego z interferometru złożonego uzyskuje się stosunkowo prosto, zakładając źródło punktowe, jednakowe i symetryczne filtry w.cz. A_k(f + f_o) = A(|f| + f_o), rzeczywiste charakterystyki anten G_k = G*_k oraz niezależność widma promieniowania i charakterystyk anten od częstości. Mianowicie, w tej sytuacji część rzeczywista w wyrażeniu (43) będzie proporcjonalna do sumy (po wszystkich k i l) wyrażeń typu:

Gk(ξo – ξk,fo) Gl(ξo – ξl,fo) ∫ Δf/2 –Δf/2  |A'(f)|2cos[2πf(τk – τl)]df·cos[2πfo(τk – τl)]

co, przy dostatecznie wąskiej wstędze Δf, upoważnia do przepisania wzoru (43) w postaci:

V(ξ1,ξ2,...,ξN,τ1,τ2,...,τN) ~ Σ k,l  GkGlcos[2πfo(τk – τl)] =

= [ Σ Gkcos(2πfoτk) ] 2   + [ Σ Gksin(2πfoτk) ] 2   ,

(45)

gdzie G_k = G_k(ξ_o – ξ_k,f_o) (tutaj ξ_o jest cosinusem kierunkowym źródła, a ξ_k — kierunku maksimum wzmocnienia charakterystyki k-tej anteny). Sygnał wyjściowy w takiej formie przewidziałem wcześniej (B o r k o w s k i 1977) posługując się znacznie prostszą analizą. Wzór typu (45) posłużył wtedy do analizy wpływu promieniowania odbitego od ziemi przed antenami na przebieg obserwacji Słońca w ciągu roku. Zasadność takiego zastosowania wynika z tego, że sygnały odbite dochodzące do anten można potraktować tak, jak gdyby były odebrane przez inne anteny (będące lustrzanymi odbiciami anten istniejących względem płaszczyzny odbijającej promieniowanie). W ten sposób interferometr dwuantenowy w obecności odbić można taktować tak, jak interferometr złożony z większej ilości anten.

Warto zauważyć, że wyrażenia (43), (44) i (45) są niezmiennicze względem przesunięcia w czasie (istotne są tam tylko fazy względne). Pozwala to położyć na jedno z zapóźnień τ_k wartość zero.

LITERATURA

B o r k o w s k i, K.M., 1976, Post.Astr., 24, 15.

B o r k o w s k i, K.M., 1977, Post.Astr., 25, 135.

B o r k o w s k i, K.M., 1979, praca doktorska, UMK, Toruń.

B o r k o w s k i, K.M., 1980, Post. Astr., 28, 15.

B o r n, M., W o l f, E., 1964, Principles of Optics, Pergamon, N. Y.

B r a c e w e l l, R.N., 1965, The Fourier Transform and Its Applications, McGraw-Hill, N. Y.

B r o u w, W.N., 1968, w: Synthesis Radio Telescope Project, I.T.R.-62 (Leiden).

C a n n o n, W.H., 1978, Geophys. J. R. Astron. Soc., 53, 503.

C a r t e r, W.H., S o m e r s, L.E., 1976, IEEE Trans. Antennas Prop., 24, 815.

C o l e, T.W., 1979, J. Opt. Soc. Am., 69, 554.

E l s m o r e, B., K e n d e r d i n e, S., R y l e, M., 1966, M.N.R.A.S., 134, 87.

E s e p k i n a, N.A., K o r o l' k o v, D.W., P a r i j s k i j, Yu.N., 1973, Radioteleskopy i radiometry, Nauka, M.

K n o c h, L., E k i e r t, T., 1979, Modulacja i detekcja, WKŁ, Warszawa.

K o, H.C., 1967, IEEE Trans. Antennas Prop., 15, 10.

K r a u s, J.D., 1966, Radio Astronomy, McGraw-Hill, N. Y.

K u l i k o v, K.A., 1961, Kurs sfericheskoj astronomii, G.I.F.-M.L., M.

R o g e r s, A.E.E., 1976, Meth. Exper. Phys., l2C, 139.

R y l e, M., 1952, Proc. Royal Soc. (London), 211A, 351.

S o l e c k i, T., 1974, praca magisterska, UMK, Toruń.

S w e n s o n, G.W., M a t h u r, N.C., 1968, Proc. IEEE, 56, 2114.

S w i e s z n i k o w, A.A., 1965, Podstawowe metody funkcji losowych, PWN, Warszawa.