RT32 — K. Borkowski, Z. Bujakowski
(Ostatnia aktualizacja: 2003.08.06)
II.1 Opis konstrukcji
32-metrowa antena jest dziełem wielu zespołów z całej Polski.
Założenia
do projektu opracowali radioastronomowie toruńscy. Projektantem głównym
był, podobnie jak w przypadku poprzedniej 15-metrowej anteny,
mgr inż. Zygmunt Bujakowski. Przy pracach projektowych
wykorzystano także doświadczenia specjalistów z kilku zagranicznych
ośrodków związanych z budowaniem instrumentów radioastronomicznych
(m.in. z Jodrell Bank, Cambridge, Rutherford Appleton Laboratory i Bonn).
|
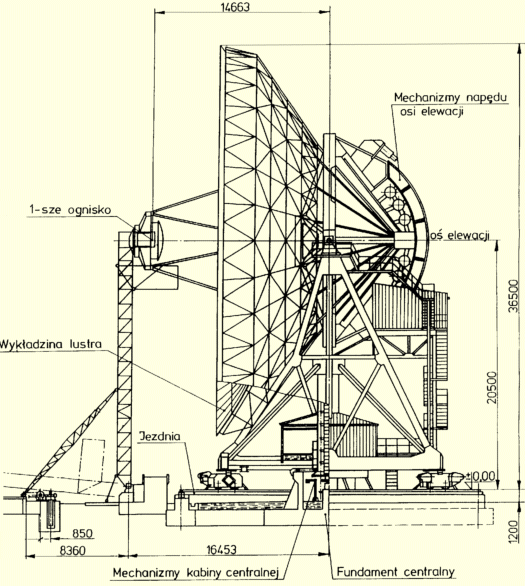
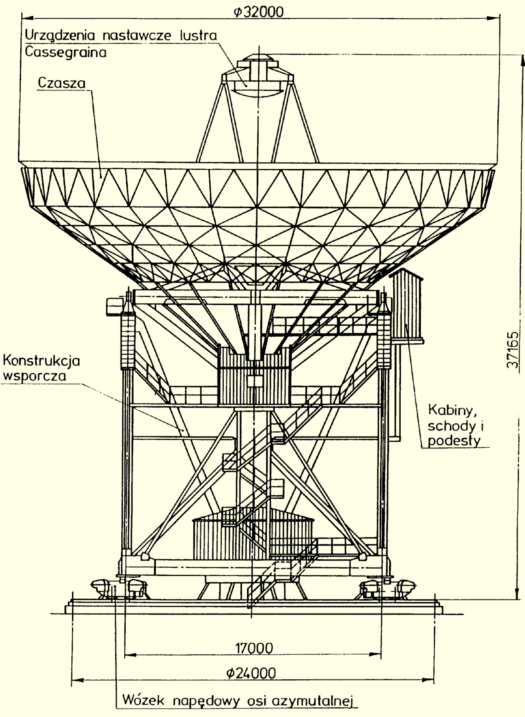
Rys. II.1: Schemat konstrukcyjny radioteleskopu 32-metrowego
– widok w pozycji serwisowej |
Teleskop ten jest w pełni sterowalną anteną o montażu horyzontalnym, z
reflektorem głównym o średnicy 32 m i pracującą w klasycznym układzie
Cassegraina z demontowalnym hiperbolicznym lustrem wtórnym o średnicy 3,2 m.
Na reflektor główny, w kształcie paraboloidy obrotowej, składa się 336
paneli ułożonych w siedmiu koncentrycznych pierścieniach. Wszystkie panele
mają taką samą długość (2,24 m) a szerokość zależną od
przynależności do jednego z siedmiu pierścieni (1,2 ÷ 1,6 m) i
wykonane są z blachy aluminiowej o grubości 2,5 mm przynitowanej do ramy
zbudowanej z aluminiowych teowników. Blasze nadano odpowiedni kształt
(wycinka paraboloidy) wstępnie poprzez mechaniczne naciąganie na specjalne
kopyto, a później za pomocą 39 śrub naciągowych pozwalających korygować
powierzchnię panelu przez
odkształcanie ramy, na której jest zamocowana blacha. Średniokwadratowa
odchyłka powierzchni paneli od paraboloidy wynosi mniej niż 0,35 mm.
Panele są mocowane do konstrukcji teleskopu na czterech regulacyjnych
śrubach umieszczonych w narożnikach panelu. Po ostatecznej justacji
dalmierzem laserowym i metodami geodezynymi pomiary wykazały dokładność
0,2 mm ustawienia paneli względem siebie.
 |
|
Rys. II.2: Schemat konstrukcyjny radioteleskopu 32-metrowego
– widok w pozycji bazowej | |
Sterowanie odbywa się wokół dwóch osi – stałej pionowej i
ruchomej poziomej z absolutną dokładnością 0,001°. Bieżącą
kontrolę położenia anteny oraz prędkości ruchu zapewniają 19-bitowe
przetworniki kąta umieszczone bezpośrednio na osiach obrotu.
Celem wyeliminowania luzów w napędach zastosowano system podwójnych
silników w każdym zespole napędowym, pracujących w trybie
antibacklash, polegającym na tym, że w każdym napędzie są
po dwa silniki, z których gdy jeden napędza, to drugi hamuje
(z siłą ok. 10 % nominalnego ciągu wynoszącego 27,5 Nm).
Z powodu istnienia zmiennych odkształceń grawitacyjnych lustra
głównego wprowadzono dodatkowy ruch kompensacyjny lustra wtórnego.
W sumie sterowanie radioteleskopu oparte jest na 8 silnikach w osi azymutu (ruch wokół pionu), 4 – w osi wysokości (oś pozioma) oraz 5
– w mechanizmach ruchu lustra Cassegraina. System sterowania obejmuje
też komputer nadzorujący (HP435rt), szereg sterowników i kontrolerów
oraz zespoły napędowe (firmy Lenze).
Cała konstrukcja nośna zamontowana jest na czterech dwukołowych
(koła mają średnicę 1,25 m) wózkach napędzanych podobnie jak w
osi wysokości (takie same silniki i kompensacja luzów). Wózki poruszają
się po jezdni – grubej szynie w kształcie dwuteownika
– rozłożonej na kole o średnicy 24 m.
|
|
Charakterystyka techniczna 32 m radioteleskopu
| Typ | sterowalna antena paraboliczna |
|
|
| Optyka do ok. 1 GHz | ognisko pierwotne |
|
| — powyżej ok. 1 GHz | system Cassegraina |
|
| Średnica torowiska | 24,0 | m |
| Największa wysokość (powyżej fundamentu) | 37,6 | m |
| Panele: liczba (7 pierścieni) |
64+64+64+64+32+32+16 = 336 |
|
| — rozmiary | 224×(120 ÷ 160) |
| cm |
| Dokładność wykonania paneli czaszy (rms) | < 0,35 | mm |
| — ustawienia względem wzorca obrotowego (rms) | 1,0 | mm |
| — czaszy po justacji dalmierzem laserowym i teodolitem (rms) | 0,2 | mm |
| — wykonania subreflektora (rms) | 0,05 | mm |
| — ustawienia osi subreflektora względem paraboloidy (max) | 0,1 | mm |
| — poziomowania torowiska (max) | 0,3 | mm |
| — poziomowania osi wysokości (max) | 0,3 | mm |
| Grawitacyjne odkształcenia (brzeg czaszy; max) |
4,2 | mm |
| Odstępstwa od homologii w położeniu zenitalnym (rms) |
0,11 | mm |
| — — — — — horyzontalnym (rms) | 0,14 | mm |
| Zakres obrotu w osi wysokości | +2 ÷ +95 | ° |
| — — — — azymutu (od południka) | ±270 | ° |
| — ruchu subreflektora wzdłuż osi | ±60 | mm |
| — obrotu subreflektora wokół dwóch osi | ±5 | ° |
| Szybkość ruchu czaszy w osi wysokości |
0,004 ÷ 14,7 | °/min |
| — — — — — azymutu |
0,008 ÷ 31 | °/min |
| Dokładność śledzenia (w obu osiach) | 0,002 | ° |
| Blokowanie apertury przez subreflektor i jego podpory | 7,44 | % |
| Obciążenie na torowisku | ~620 | t |
| — na osi wysokości (w tym przeciwwaga: ~90 t) | ~320 |
t |
| Ciężar wyposażenia elektrycznego | ~2 | t |
| — urządzeń w kabinie centralnej (pod anteną) | 9,4 | t |
| — stalowych szyn (o szerokości 180 mm) | 42,5 | t |
| — konstrukcji do montażu i konserwacji subreflektora | ~16 | t |
| Dopuszczalna szybkość wiatru podczas użytkowania | 16 | m/s |
| Graniczna szybkość wiatru grożąca uszkodzeniem | 56 | m/s |
| Dopuszczalna grubość oblodzenia | 2 | cm |
| — zakres temperatur | –25 ÷ +35 | °C |
|
|
Większość prac obserwacyjnych prowadzona jest w systemie
Cassegraina, na co zezwala obecność hiperbolicznego lustra wtórnego
o średnicy 3,2 m umieszczonego między ogniskiem paraboloidy a głównym
reflektorem. Promieniowanie kosmiczne,
po odbiciu od paraboloidy i lustra wtórnego, skupia się w ognisku
wtórnym, gdzie umieszcza się właściwe anteny, tzw. oświetlacze,
i systemy odbiorcze. Ze względu na dużą liczbę pasm używanych w praktyce
VLBI i częste zmiany obserwowanych częstości – nawet w czasie jednej
sesji obserwacyjnej – najważniejsze systemy odbiorcze są na stałe
instalowane w pobliżu ogniska wtórnego. Wybór właściwego oświetlacza
następuje przez odpowiedni przechył lustra Cassegraina. Istnieje też
możliwość obserwacji w trybie ogniska pierwotnego (w zasadzie na
dłuższych falach, λ ≥ 50 cm). W tym celu przewidziano
specjalne urządzenie do demontowania lustra Cassegraina i instalowania
tam urządzeń odbiorczych (w kabinie ogniska pierwotnego).
Niezwykle ważną charakterystyką teleskopu jest dokładność wykonania
reflektorów, gdyż decyduje ona o jego użyteczności na
krótkich falach. Wiadomo, że jeśli błąd średniokwadratowy (rms)
powierzchni luster wynosi σ, to traci się
na skuteczności wykorzystania apertury anteny o czynnik:
Często przyjmuje się, że radioteleskop jest użyteczny do fal λ = 16σ,
kiedy jego skuteczność maleje do 54 % (o czynnik ησ =
0,54)1.
Szacunkowa dokładność głównego reflektora teleskopu 32-metrowego wynosi
0,4 mm, co oznacza dużą sprawność na fali 7 mm i możliwą używalność
na 3 mm (ok. 100 GHz).
II.2 Geometria i inne charakterystyki
Geometrię anteny w pełni określają cztery parametry:
średnica reflektora głównego (d), długość ogniskowej (f),
średnica reflektora wtórnego (subreflektora, ds) i położenie
ogniska wtórnego, np. jego odległość od wierzchołka paraboloidy
(h). Pozostałe parametry można obliczyć z zależności
matematycznych podanych w załączonej tabeli.
|
|
Parametry geometryczne radioteleskopu
| Główny reflektor (paraboloida) |
|
| Średnica d | 32,0 | m |
| Odległość ogniskowa f | 11,2 | m |
| Stosunek ogniskowej do średnicy f/d | 0,35 |
| Głębokość czaszy H = d2/(16f) | 5,7143 | m |
| Kąt rozwarcia 2Θo
= 4arctg[d/(4f)] | 142,1507 | ° |
| Powierzchnia całkowita
8πf2[cos–3(Θo/2)–1]/3 | 899,45 | m2 |
| Apertura (powierzchnia zbierająca) πd2/4 | 804,25 | m2 |
Równanie paraboli†
r = √{4f(f–z)} = 2f tg(Θ/2)
|
|
|
Radioteleskop w układzie Cassegraina |
|
| Średnica hiperbolicznego subreflektora ds | 3,2 | m |
| Wysokość ogniska wtórnego nad wierzchołkiem czaszy h | 1,0 | m |
| Kąt rozwarcia subreflektora
2Φo
= 2arcctg{2[(f–h)/ds
– (f–H)/d]}
| 18,8256 | ° |
| Efektywna ogniskowa F =
d/[4tg(Φo/2)] |
97,1729 | m |
| Powiększenie radioteleskopu F/f |
8,6762 | |
| Odległość ognisk 2c = f–h | 10,2 | m |
| Mimośród hiperboli c/a = (F+f)/(F–f) |
1,2605 | |
| Nachylenie asymptoty
α
= arccos(a/c) = arccos[(F–f)/(F+f)] |
37,5044 | ° |
| Odległość wierzchołka hiperboloidy od ognisk c+a | 9,1459 | m |
|
c–a |
1,0541 | m |
| Odległość ognisko pierwotne – brzeg subreflektora
ρ =
ds/(2sinΘo) |
1.6914 | m |
| Głębokość subreflektora c–a–(f–H)ds/d |
0,5056 | m |
| Różnica dróg optycznych do obu ognisk
(f–h)a/c |
8,0917 | m |
| Całkowita
powierzchnia subreflektora |
| πsinα[(ρ+a)√{ρ(ρ+2a)}–2a2ln | √ρ
+ √{ρ+2a}
√{c+a}+√{c–a} | ]–π(c2–a2) |
|
8.7728 | m2 |
| Powierzchnia cienia subreflektora na aperturze
πds2/4 | 8,0425 | m2 |
| Równanie hiperboli†
r = √{(c2–a2)[(c/a–z/a)2–1]}
= (c2–a2)sinΘ/(a+c cosΘ) |
|
|
† r jest
odległością od osi symetrii radioteleskopu, wzdłuż której mierzona jest
współrzędna z, poczynając od ogniska paraboloidy (pokrywającego się z
jednym z ognisk hiperboloidy) i dodatnio w kierunku czaszy.
Θ jest kątem pomiędzy osią z i promieniem
wodzącym.
|
Własności użytkowe radioteleskopu zależą od częstości obserwacji.
Napięciową charakterystykę kierunkową wyznacza transformata Fouriera
z rozkładu pola elektrycznego na aperturze instrumentu. W przypadku apertury
o symetrii kołowej dwuwymiarowa transformata Fouriera sprowadza się do
transformaty Hankela. Dla teleskopu, którego apertura
ma kształt koła z otworem w środku, znormalizowaną charakterystykę
napięciową można wyrazić w przybliżeniu (dokładne rozwiązanie podano
w
tym dokumencie) wzorem:
|
U(x) = |
2d2
(d2 –
ds2)x |
| { |
J1(x) + |
β
2 – β
|
J3(x)
– |
ds
d
|
| [ |
J1( |
xds
d
| )
+ |
β
2 – β
|
J3( |
xds
d
|
) | ] | } |
, |
| (II.1) |
gdzie:
Jn są funkcjami Bessela pierwszego rodzaju,
x = π(d/λ)sinθ,
λ = c/ν jest długością fali obserwowanego
promieniowania o częstości ν (tutaj c jest prędkością światła),
θ to kąt między danym kierunkiem a osią symetrii,
β charakteryzuje oświetlenie apertury przyjęte w postaci funkcji:
1 – β(2r/d)2,
w której r jest odległością od osi symetrii do danego miejsca na aperturze.
W U(x) składniki z funkcją J1 odpowiadają za równomierny rozkład
pola, a składniki z J3(x) — za rozkład ważony funkcją 1
– β(2r/d)2.
Charakterystykę mocy promieniowania takiej anteny można zapisać w formie
|
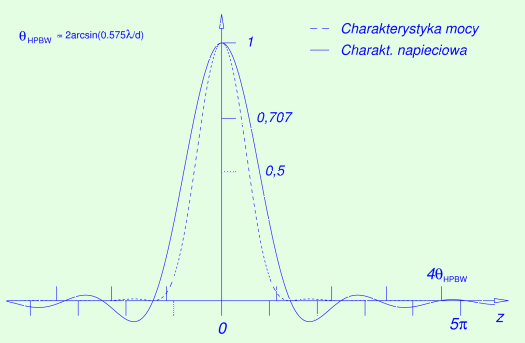
Rys. II.3: Kierunkowa charakterystyka promieniowania apertury w kształcie
pierścienia o średnicy wewnętrznej 10 razy mniejszej od zewnętrznej (d)
oświetlonej słabnąco ku brzegom jak 1 –
3(r/d)2. Charakterystyka napięciowa (krzywa ciągła) ma
postać wzoru (II.1) z β
= 0,75. Linia przerywana przedstawia moc promieniowania — jest to
kwadrat funkcji (II.1).
ΘHPBW
jest oznaczeniem na szerokość połówkową głównego listka
charakterystyki mocy |
Rozdzielczość kątową, czyli szerokość głównej wiązki
charakterystyki kierunkowej na połowie mocy (HPBW), określa
podwojony kąt θ =
arcsin[xλ/(πd)],
przy którym moc P
spada do połowy wartości maksymalnej. Dla paraboloidu o średnicy
d = 32 m z obliczeń numerycznych otrzymujemy:
|
ΘHPBW = 2arcsin(1,80706 |
λ
πd
|
) ≈ 1,15[rad] |
λ
d |
= 1,24' |
λ
[cm] |
= 37' |
[GHz]
ν |
. |
|
Współczynnik liczbowy 3,614/π = 1,15
jest właściwy dla oświetlenia w postaci 1 – 3(r/d)2
(tj. z 12 dB tłumieniem na skraju czaszy), oraz dla
d/ds = 10. Rozdzielczości 32-metrowego teleskopu dla
kilku typowych częstości (ν) zawiera
poniższa tabelka.
Teoretyczna rozdzielczość kątowa
[ΘHPBW = 2arcsin(0,5752λ/d)] paraboloidu
o średnicy d = 32 m
z subreflektorem (o średnicy d/10) oraz jego kierunkowość
|
| ν
[MHz] | 327 | 408 | 610 |
1420 | 1660 | 2290 | 5000 | 11700 |
22 000 | 30 000 | 100 000 |
| λ [cm] |
91,7 | 73,5 | 49,1 |
21,1 | 18,1 | 13,1 | 5,996 | 2,562 |
1,363 | 0,999 | 0,300 |
|
| ΘHPBW
['] |
113 | 90,8 | 60,7 | 26,1 | 22,3 |
16,2 | 7,41 | 3,17 | 1,68 |
1,24 | 0,371 |
| [°] | 1,89 | 1,51 | 1,01 | 0,435 | 0,372 | 0,270 | 0,124 | 0,053 | 0,028 | 0,021 | 0,006 |
|
| D/1000 | 11 | 17 | 37 | 202 | 276 | 526 | 2510 | 13700 | 48500 | 90200 | 1000000 |
|
|
|
|
|
Innymi ważnymi charakterystykami radioteleskopu są jego
powierzchnia skuteczna i kierunkowość. Jeśli
przez kąt bryłowy charakterystyki kierunkowej określimy
wielkość:
|
ΩA= |
∫
4π
|
Pn(θ,φ) dΩ
≈ 2π |
π/2
∫
0
|
|
P(θ)
Pmax
|
sinθ dθ, |
|
gdzie Pn jest mocą
znormalizowaną wartością w kierunku maksimum promieniowania,
Pmax,
to kierunkowość D obliczymy
z zależności:
D wyraża przybliżoną liczbę
radioźródeł, jaką antena może
rozdzielić przy równomiernym ich rozkładzie na niebie
(w praktyce liczba tych źródeł jest o około rząd wielkości mniejsza),
zaś Aeff to skuteczna
powierzchnia anteny, która w danym
przypadku (przy wyżej przyjętym modelu charakterystyki) wynosi:
Powyższa wielkość nie uwzględnia tzw. omowych strat sygnału, strat na
skutek rozpraszania na nieidealnych lustrach i wynikających z cienia
rzucanego przez podpory lustra wtórnego. W praktyce powierzchnię skuteczną
wyznacza się z obserwacji radioźródeł o znanych gęstościach strumienia
promieniowania. Jeśli źródło o gęstości strumienia F wywoła
tzw. temperaturę antenową (patrz rozdz. VII)
TA to:
gdzie k jest stałą Boltzmanna.
II.3 Cienie lustra wtórnego i jego podpór
Od strony długich fal ograniczeniem użyteczności tego teleskopu
jest efekt blokowania (przesłaniania) powierzchni reflektora przez
konstrukcję nośną urządzeń instalowanych w ognisku pierwotnym. Zjawisko
to staje się coraz groźniejsze w miarę jak rośnie długość fali.
Można przyjąć, że oświetlacze są całkowicie przesłonięte przez
podpory, gdy średnia odległość podpór sięga ok. pół długości
fali. To kryterium zezwalałoby na obserwacje nawet na częstościach
znacznie poniżej 100 MHz, ale na dolną granicę przewidziano
najniższą ze standartowych częstości VLBI — 327 MHz.
Czynnik blokowania powierzchni pozostaje jednak ważny z powodu wpływu
na skuteczność wykorzystania apertury. Ocenia się, że skuteczność
anteny maleje o czynnik
|
ηb
= | ( |
1 – |
powierzchnia zablokowana
całkowita powierzchnia apertury |
) |
2
|
. |
|
Na powierzchnię zablokowaną składają się trzy przyczynki: (1) prosty
cień subreflektora, (2) prosty cień jego podpór i (3) przesłanianie
promieniowania już odbitego od zwierciadła głównego na drodze w kierunku
ogniska. Pierwsze dwie składowe jest dość łatwo wyznaczyć, natomiast
trzeci składnik może sprawiać pewne trudności – zwłaszcza w
konstrukcjach, w których podpory nie leżą w płaszczyznach przechodzących
przez oś paraboloidy (tak jest w naszym teleskopie posiadającym 8 podpór
lustra Cassegraina).
Szczegółowe
obliczenia analityczne i w oparciu o graficzne rzutowanie
wykazują w sumie ok. 7,44 % strat apertury, co czyni ok.
14 % strat w skuteczności anteny wywołanych blokowaniem apertury.
|
Składniki cienia na 1/8 apertury |
| Źródło cienia | Rozmiary
[m] | Powierz-
chnia [m2] |
| Lustro wtórne | π×1,62/8 | 1,0053 |
| Ramię ukośne zawieszenia lustra |
~0,150×1,10 |
0,1650 |
| Końcówka ramienia |
0,100×0,42 |
0,0420 |
| Podpora – cieńsza część (rzut prosty) | 0,114×1,97 | 0,2246 |
| Podpora – grubsza część (rzut prosty) | 0,159×2,28 | 0,3625 |
| Podpora – przesłanianie ogniska | obl. analit. | 5,6407 |
| Razem powierzchnia cienia |
| 7,4821 |
|
| W procentach apertury 100×8×7,4821/804,25 = 7,44 |
|
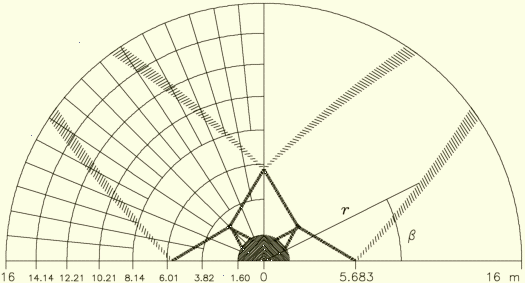
Rys. II.4:
Rozkład
paneli i blokowanie apertury toruńskiego radioteleskopu
32-metrowego. Na rysunku zachowano skalę. Obszar jaśniej zakreskowany
(cień zewnętrzny) ma powierzchnię 22,56 m2, zaś ciemniejszy —
7,62 m2. Krzywe opisujące brzegi zewnętrznego cienia jednej
podpory mają postać β(r) =
βo –
arccos[r/(2ro) –
2f2/(rro)],
gdzie f jest ogniskową (11,2 m), a βo i ro wynoszą
2,3345 rad i 60,987 m dla jednej strony cienia zaś 2,2789 rad
i 62,043 m — dla drugiej |
II.4 Martwy obszar przy zenicie
Montaż horyzontalny ma tę własność, że istnieje pewien niewielki obszar
na niebie w pobliżu zenitu, gdzie azymutalny napęd teleskopu nie nadąża
za ruchem dziennym obiektów niebieskich. Wynika to z faktu, że azymut
każdego obiektu przechodzącego przez sam zenit zmienia się w nieskończenie
krótkim czasie z 270° (albo –90°) na 90°.
Ogólniej: im bliżej obiekt mija zenit (punkt osobliwy), tym szybsze
są zmiany azymutu.
Można
pokazać, że przy szybkości teleskopu w azymucie sięgającej
30°/min owa ,,ślepa plama" w okolicy zenitu, gdzie (azymutalna)
szybkość źródeł przewyższy tę wartość, ma rozmiary ok.
0,5°×1,5°.
|
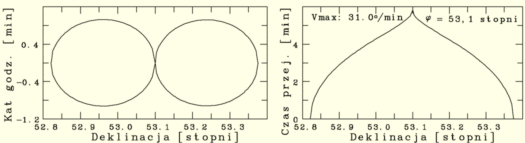
Rys. II.5: Z lewej: wokółzenitalny obszar, w którym
średnia szybkość zmiany azymutu źródeł kosmicznych jest
większa od 31°/min na szerokości geograficznej
φ = 53,1°. Z prawej: czas potrzebny
na dogonienie źródła. Symetrie względem deklinacji równej
φ są tylko pozorne i wynikają z
małości różnic |
Szybkość zmiany azymutu A obiektów poruszających się ruchem
dziennym sfery niebieskiej wynosi:
|
|
.
A
|
= |
sinφ –
sinδ cos z
sin2z
|
= sinφ + cosφ |
cosA
tg z
|
, |
|
gdzie φ jest szerokością geograficzną
(geodezyjną), δ —
deklinacją obiektu, a z — jego odległością zenitalną (tj.
dopełnieniem do π/2 kąta wysokości
albo elewacji). Obszar krytyczny,
w którym teleskop nie nadąży za źródłem, dla
teleskopu o maksymalnej prędkości V — wyrażonej w jednostkach
naturalnych, tj. rad/rad, albo (obroty teleskopu)/(obroty nieba), i
przyjmującej znak minus dla obiektów górujących między zenitem
a biegunem nieba — mieści się pomiędzy okręgami deklinacyjnymi:
|
δ± = φ –
arctg |
cosφ
±V –
sinφ
|
, |
|
a więc obejmuje pas o szerokości ~2cosφ/V.
W szczególności, dla Piwnic i V = 120 (tzn. 30°/min) otrzymujemy
δ– – δ+ = 34,4'.
Kąt godzinny, przy którym śledzony obiekt ucieknie teleskopowi
można obliczyć elementarnie w sposób ścisły (np. równanie (9) w
tej pracy),
ale dla praktycznych zastosowań takie rozwiązanie jest zbyt złożone.
Bardzo dobrze przybliża je jednak następujące proste wyrażenie:
Wielkość Ao ≈ – arccos√{(φ
– δ)
(±V – sinφ)/cosφ}
stanowi odpowiedni kąt azymutu. Oba te kąty opatrzono znakiem
minus, gdyż obiekt znajduje się na wschód od południka.
Przypis:
1Niekiedy
za najmniejszą długość fali bierze się 4πσ,
przy której skuteczność wykorzystania powierzchni wynosi 1/e, tj. ok.
37 %.
File translated from
TEX
by
TTH,
version 3.40 on 04 Aug 2003.