Letter to the Editor

ELP 2000-85 and the Dynamical Time – Universal Time relation

K.M. Borkowski

Torun Radio Astronomy Observatory, Nicolaus Copernicus University,
ul. Chopina 12/18, PL-87-100 Torun, Poland

Received June 21, Accepted July 14, 1988

Summary. The new ephemeris of the Moon, ELP 2000-85, has been used to analyse some of more reliably documented historical eclipses of the Sun. The conclusion is that the presently available expressions of the Dynamical Time – Universal Time (DT – UT) difference are clearly inadequate for the use with this ephemeris for historical studies. The basic reason lies in the difference between mean lunar longitude in the new and older theories of the motion of the Moon. A provisional relation between the two times applicable presumably before about AD 1700 (back to about 2000 BC) reads in seconds of time

DT – UT = 35.0 (t + 3.75)² + 40,

where t is time in Julian centuries elapsed from the epoch 2000.0. This equation includes a magnitude of the secular deceleration of the Earth rotation of 70 s/cy² or, in other units, 22 10^–9 /cy.

Key words: Ephemerides – eclipses – Earth:rotation – time

With the appearance of the new theory of the motion of the Moon worked out in the Bureau des Longitudes (Chapront-Touzé and Chapront, 1983) recently emerged relatively simple, yet very accurate, semianalytical ephemeris of this body named ELP 2000-85 (Chapront-Touzé and Chapront, 1987, 1988), which seems very suitable for studies of historical observations of occultations and solar and lunar eclipses. Over a few thousands of years (since –1500) its internal accuracy is 10" or better, as compared to the JPL numerical integration LE51. Since the authors offer a ready FORTRAN coding of the ELP 2000-85 it may be expected that in the near future this ephemeris will become a sort of standard tool in analyses of ancient astronomical observations. Some of such analyses require the knowledge of the difference between the Dynamical Time (DT), which is the argument of the discussed ephemeris and is a direct extension of the Ephemeris Time (these two times can be considered equivalent for our purposes), and the Universal Time (UT).

The authors of ELP 2000-85 on passing suggested (in Chapront-Touzé and Chapront, 1988) to use the relation DT – UT derived by Morrison and Stephenson (1982), which is based on Babylonian observations of the eclipses of the Moon. I have used this relation in another study (Borkowski, 1988) and I found it to be indeed very acceptable, at least when the solar eclipses are concerned and older theories of the motion of the Moon used. However, in conjunction with the French ephemeris (ELP 2000-85) the suggested relation fails to give satisfactory predictions of ancient solar eclipses (and presumably also other astonomical phenomena, which I did not analyse). In fact, it should not be surprising because this ephemeris uses considerably different expression for the mean lunar longitude than does e.g. the Improved Lunar Ephemeris. In particular, it incorporates the secular tidal acceleration of the Moon of –23.895 "/cy², while more commonly used value reads –26 "/cy².

To estimate the quantity ΔT = DT – UT I have used the solar eclipses recorded in historical times between –2136 and 1715 of the common era, most of which were presented by Stephenson and Clark (1978). Firstly, I analysed in detail each eclipse with the aim to estimate a range of ΔT values that satisfy the stated condition of centrality. In two cases, concerning partial eclipses of 928 at Baghdad and –321 at Babylon, angular (altitude of the Sun) or timing information (duration of eclipse that occurred at sunset) from ancient records were used as landmarks for ΔT estimates. For this purpose I made use of the computer program described in Borkowski (1988) with original less accurate ephemerides replaced by ELP 2000-85 (a FORTRAN programmed version supplied by its authors which I slightly modified to fit my philosophy and to include the nutation theory) and the Stumpff's algorithm for the motion of the Earth (Stumpff, 1979, 1980; also this algorithm I extended by adding the nutation to get the apparent coordinates of the Sun). Then a least squares fit of the estimated ΔT values to the quadratic polynomial in time was performed. The usual method of fit I modified so as to carry minimization of the summed squares of deviations above or below the mentioned range of acceptable ΔT values, rather than deviations from certain point inside the range. This procedure effectively eliminates observations that are not critical for the determination of ΔT curve.

Table 1. Eclipses of the Sun used for derivation of DT – UT difference. The 'fit' denotes values obtained from Eq. (1) and 'res.' stands for the deviation outside the 'min.' (usually the second contact) to 'max.' (usually the third contact) range. The 'computed' data correspond to the 'fit' values of DT – UT. The 'observed' phases of 1 or >1 refer to a totality, while these of the form >0.9... to an annular eclipse

_______________________________________________________________________ Date Place DT - UT [s] Eclipse phase Year M D min. max. fit res. observed computed _______________________________________________________________________ 1715 05 03 England* -23 -11 69 -80 1 0.997/1.003 1567 04 09 Roma 86 158 52 34 1 0.998 1560 08 21 Coimbra -523 179 55 0 >1 1.008 1485 03 16 Melk -4540 2040 108 0 >1 1.020 1415 06 07 Prague -1500 628 194 0 >1 1.016 1406 06 16 Braunschweig -198 1400 207 0 >1 1.014 1267 05 25 Constantinopole -810 736 488 0 >1 1.003 1241 10 06 Stade/Cairo(?) 521 1007 554 0 >1 1.000/1.017 1239 06 03 Southern Europe 718 1200 560 158 >1 0.993-1.036 1221 05 23 Kerulen River <-5400 1043 610 0 >1 1.011 1176 04 11 Antioch -348 1482 745 0 >1 1.022 1124 08 11 Novgorod 837 2571 916 0 >1 1.002 1133 08 02 Salzburg 146 1334 885 0 >1 1.025 975 08 10 Kyoto 954 4295 1516 0 >1 1.007 968 12 22 Constantinopole 1411 4680 1546 0 >1 1.001 928 08 18 Baghdad** 1357 1615 1737 -122 0.218 912 06 17 Cordoba(?) 1007 2453 1817 0 >1 1.022 840 05 05 Bergamo <-3780 6238 2195 0 >1 1.012 522 06 10 Nan-ching(?) 3046 4678 4295 0 >1 1.018 516 04 18 Nan-ching(?) 3146 4730 4343 0 >0.939 0.953 120 01 18 Lo-yang 7604 8474 7967 0 >1 1.014 65 12 16 Kuang-ling 8334 8838 8547 0 >1 1.010 -135 04 15 Babylon 10336 11272 10878 0 >1 1.021 -180 03 04 Ch'ang-an 10990 11932 11441 0 >1 1.020 -197 08 07 Ch'ang-an 5650 11716 11651 0 >0.950 0.951 -321 09 26 Babylon*** 13200 13322 13285 0 0.087 -548 06 19 Chu-fu 15751 19789 16560 0 >1 1.010 -600 09 20 Ying(?) 17323 18105 17357 0 >1 1.001 -708 07 17 Chu-fu 19091 20045 19082 9 >1 0.999 -1374 05 03 Ugarit 30638 31760 31512 0 >1 1.004 -2136 10 22 An-yi**** 49261 50216 49528 0 >0.967 0.976 _______________________________________________________________________

Notes to Table 1: * — at Darrington and Lewes (the path of totality limits); ref.: Morrison et al. (1988) ** — DT – UT estimated from observed altitude of the Sun of about 12 (+/–0.5) deg; computed value is 11.0 deg. *** — DT – UT estimated from observed duration of this eclipse of about 12 (+/–1) min. (till sunset); computed value is 12.5 min. **** — Ref.: Wang and Siscoe (1980) and P.K. Wang (1988, private communication); assumed geographical coordinates were 35.1 (latitude) and 111.2 deg (longitude) ? — uncertain location

As a result of the above described fit the following expression for DT (in seconds) has been established:

DT – UT = 35.0 (t + 3.75)2 + 40,

(1)

where t is time measured in Julian centuries since 2000.0. Table 1 and Fig. 1 contain details of the analysed data and final residuals. Eq. (1) differs from that of Morrison and Stephenson (1982) by varying amount and up to about 25 minutes of time in the considered historical period (the maximum is reached near 700 BC). Though, due to limited observational material, I am not in position to claim this equation to be definite, I believe it is good to a few

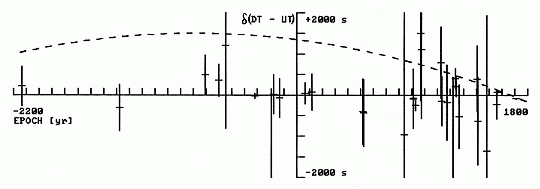Fig.1. Plot of allowed ranges of the DT – UT differences for eclipses of Table 1 relative to the mean ΔT curve [Eq. (1)] represented here by the abscissa axis. The abscissa axis is scaled every 100 years from –2200 to 1800, and the ordinate axis is marked every 500 s between the range of +/–2000 s. Each vertical bar is halved by a short horizontal bar to mark the centre of the allowed range. The broken curve shows the ΔT of Morrison and Stephenson (1982)

minutes over the entire period and thus may prove useful for researchers who need such relation immediately. The numerical coefficient of 35.0 s/cy² in the formula for ΔT is interpreted as one half of the secular deceleration of the Earth rotation. It will be noted that our value of 70 s/cy² or, in relative angular units, 22^.10^–9/cy does not differ much from other authors' determinations which range from about 60 to more than 90 s/cy². In fact, it is enveloped by two recent results of 65 and 72.82 s/cy² (Morrison and Stephenson, 1982, and Li Zhisen and Yang Xihong, 1985). It is difficult to assess accuracy to our result but the two following observations may be of some use. If the first eclipse listed in Table 1 is omitted in the analysis then the deceleration rises to 72.8 s/cy². Judging by the formal standard deviations of the modified least squares fit alone one arrives at the uncertainty of about 1.4 s/cy², which certainly is still too optimistic in view of the assumed modified definition of residua. In any case, the near future requires further work to be done encompassing also other historical eclipses (solar and lunar) and occultations of stars.

L.V. Morrison (1988, private communication) criticized my use of rather unreliable ancient (6th century and earlier) records of total solar eclipses. The reader will observe, however, that of them only the eclipse of –708 (Chu-fu) contributed to the solution described by Eq. (1), the remaining 12 eclipses happened not to be critical.

The ephemeris ELP 2000-85 can be modified to account for other adopted values of the lunar tidal acceleration. For comparison purposes I have used the lunar arguments listed in Table 8 (plus adequately changed expression for their L) of Chapront-Touzé and Chapront (1988) as the replacement of those originally included in the FORTRAN code of the ephemeris. The modification incorporates the tidal acceleration of –26.305 "/cy² and makes the ephemeris to closely agree with the LE51. Then, I have computed the circumstances of all the eclipses listed in Table 1 using different expressions for the ΔT. The expression of Morrison and Stephenson (1982) gave satisfactory predictions only back to 912 (excluding the Baghdad eclipse). Similarly, unsuitable with the modified lunar ephemeris appears Eq. (1) above. In contrast, a 'two-acceleration' model of Stephenson and Morrison (1984) performed much better in this respect. It only failed to predict the 'observed' (Table 1) phases at Kuang-ling, Ugarit and An-yi, which are considered to be less reliable.

Acknowledgements. I would like to thank the authors of the ELP 2000-85 for a copy of their program and associated printed materials, which made this work possible. I am also grateful to Dr Dr L.V. Morrison and M. Chapront-Touzé for helpful criticisms of, and comments on an earlier version of this letter. Prof. S. Gorgolewski kindly corrected my English.

REFERENCES:

Borkowski K.M., 1988, in preparation [Post. Astronaut., 22 (1989), 99 – 130]

Chapront-Touzé, M., Chapront, J., 1983, Astron. Astroph. 124, 50

Chapront-Touzé, M., Chapront, J., 1987, Notes Scientifiques et Techniques du Bureau des Longitudes S021, Paris

Chapront-Touzé, M., Chapront, J., 1988, Astron. Astroph. 190, 342

Li Zhisen, Yang Xihong, 1985, Scientia Sinica, Ser. A 28, 1299

Morrison, L.V., Stephenson, F.R., 1982, in Sun and Planetary System (Astrophys. Space Sci. Lib. 96), eds. W. Fricke, G. Teleki, Reidel, Dordrecht, p. 173

Morrison, L.V., Stephenson, F.R., Parkinson, J., 1988, Nature 331, 421

Stephenson, F.R., Clark, D.H., 1978, Applications of Early Astronomical Records, Adam Hilger, Bristol

Stephenson, F.R., Morrison, L.V., 1984, Phil. Trans. R. Soc. London A 313, 47

Stumpff, P., 1979, Astron. Astrophys. 78, 229

Stumpff, P., 1980, Astron. Astrophys. Suppl. Ser. 41, 1

Wang, P.K., Siscoe, G.L., 1980, Solar Phys. 66, 187