Published in: D. Behrend and A. Rius (eds.):
Proceedings of the 15th Working Meeting on European VLBI
for Geodesy and Astrometry,
Institut d'Estudis Espacials de Catalunya,
Consejo Superior de Investigaciones Científicas,
Barcelona, Spain, 2001.

ITRF2000Positions of Non-geodetic Telescopes in theEuropean VLBINetwork

Patrick Charlot⁽¹⁾, Robert Campbell⁽²⁾, Walter Alef⁽³⁾, Kazimierz Borkowski⁽⁴⁾, John Conway⁽⁵⁾, Anthony Foley⁽⁶⁾, Simon Garrington⁽⁷⁾, Alexander Kraus⁽³⁾, Axel Nothnagel⁽⁸⁾, Ojars Sovers⁽⁹⁾, Corrado Trigilio⁽¹⁰⁾, Tiziana Venturi⁽¹¹⁾, Huang Xinyong⁽¹²⁾
⁽¹⁾Observatoire de Bordeaux — CNRS/UMR 5804;
⁽²⁾Joint Institute for VLBI in Europe;
⁽³⁾Max-Planck-Institut für Radioastronomie;
⁽⁴⁾Nicolaus Copernicus University, Torun Centre for Astronomy;
⁽⁵⁾Onsala Space Observatory;
⁽⁶⁾Netherlands Foundation for Research in Astronomy;
⁽⁷⁾MERLIN/VLBI National Facility, Jodrell Bank Observatory;
⁽⁸⁾Geodetic Institute of the University of Bonn;
⁽⁹⁾Remote Sensing Analysis Systems, Inc. — Jet Propulsion Laboratory;
⁽¹⁰⁾Instituto di Radioastronomia, Stazione VLBI Noto;
⁽¹¹⁾Instituto di Radioastronomia, CNR;
⁽¹²⁾Shanghai Observatory, Chinese Academy of Sciences

Abstract: The European VLBI Network (EVN) has conducted a dedicated non-standard geodetic VLBI experiment in November 2000 with the goal of improving the positions of three non-geodetic EVN telescopes (Jodrell Bank, Torun, Westerbork). The positions of these telescopes were previously known to a few meters only, which is not sufficient for accurate processing of VLBI experiments conducted in phase-referencing mode. The observing frequency was 5 GHz, the highest common frequency available at all telescopes. Observations and data analysis are discussed with special emphasis on the effects of the ionosphere, the dominating error source in this single-frequency experiment. Assessment of the quality of the results indicates that the new estimated telescope positions are accurate to about 5 cm.

1 Introduction

The European VLBI Network (EVN) is an array of radio telescopes spread throughout Europe and Asia, which conducts VLBI observations of radio sources, generally for astrophysical purposes. Some of these telescopes also participate regularly in dual-frequency (S- and X-band) geodetic campaigns [1], and thus have highly-accurate geodetic positions. By contrast, some other EVN telescopes, not equipped with S/X radio receivers, have poorly known positions because they have never participated in such campaigns. The major telescopes in the latter category are located at Jodrell Bank (United Kingdom), Torun (Poland) and Westerbork (Netherlands).

Inaccuracy in the terrestrial coordinates of the above antennas has been a major limitation for EVN observations with the phase-referencing technique. This technique, now commonly used for imaging weak radio sources, alternates observations between a target source and a nearby calibrator, and requires accurate knowledge of the VLBI geometrical model to be successful [2]. To overcome this situation, a dedicated geodetic VLBI experiment was carried out by the EVN in November 2000, with the aim of improving those poorly known telescope positions. The following sections present the design of this non-standard geodetic experiment, the data analysis scheme, and the results of these observations. The accuracy of the new estimated telescope positions is discussed in Section 5.

2 Experiment design and observations

Observations were carried out during a 24-hour period starting at 9:30 UT on November 23, 2000, with a network consisting of four geodetic telescopes (Effelsberg, Medicina, Noto, Shanghai) and five non-geodetic telescopes located at Cambridge, Jodrell Bank, Onsala, Torun, and Westerbork. An additional geodetic antenna (Urumqi) was scheduled but could not observe because of technical problems. At Jodrell Bank, the Mk2 telescope was used, while at Onsala, the 25 m antenna (Onsala85) was employed. The option of observing with a single telescope (antenna 7) at Westerbork was preferred to using the phased-array because the effective phase centre of the array (and therefore the geodetic position) might vary when the array configuration is changed, for example if some antennas are switched in or out of the array.

Unlike standard dual-frequency geodetic observations, this experiment was carried out at the single frequency of 5 GHz, the highest frequency available at all observing telescopes. A specific bandwidth synthesis scheme recording 8 frequency channels, each 8 MHz-wide, spread over 108 MHz was designed for this experiment. This bandwidth was chosen based on the common frequency range between telescope receivers which was about 120 MHz. The individual channel frequencies were 4906.99, 4909.99, 4918.99, 4936.99, 4969.99, 4993.99, 5008.99 and 5014.99 MHz. Data from the MERLIN telescope at Cambridge were recorded at Jodrell Bank via a 200-km 28-MHz microwave link and thus had only a limited bandwidth. Due to this mode of transmission, path length variations between Cambridge and Jodrell Bank could not be measured and removed from the VLBI data in the standard automatic way.

Scheduling was carried out with the NASA SKED program in order to optimize the sky coverage at each telescope as in standard geodetic experiments. A total of 20 strong sources selected from the International Celestial Reference frame (ICRF) catalog [3], well spread in right ascension and between –25° and 80° declination, was observed for this purpose with generally 5 to 15 scans on each of them. Integration times ranged from 1 to 6 min and were set to obtain signal to noise ratios larger than 100. Low elevation observations (< 10°) were avoided to limit systematic errors caused by the ionosphere.

3 Data analysis and modeling

The raw data bits were correlated with the Mark IV data processor in Bonn, Germany, and exported through a geodetic data base file. Further analysis of the bandwidth synthesis delay and delay rate was conducted with the MODEST software [4] after converting the data into NGS format. The overall analysis strategy aimed at fixing all ``known'' parameters of the VLBI model to limit possible biases and systematic errors caused by improper knowledge of the ionosphere, which is the dominant error at this relatively low observing frequency.

Following this scheme, the coordinates of all extragalactic sources were held fixed at their ICRF values. Similarly, the coordinates of the geodetic telescopes were held fixed at their values in the International Terrestrial Reference Frame, namely the ITRF2000. The coordinates of the non-geodetic antenna Onsala85 were derived from those of the nearby geodetic antenna Onsala60 using a local tie measured with X-band VLBI in the early 1980's [5] and were also held fixed. The Earth orientation parameters were adopted from the IERS combined series C04, which is consistent at the sub-centimeter level with the above terrestrial and celestial reference frames. In all, only clocks (using a time-linear model with breaks when needed), tropospheric zenith delays (see below), and the coordinates of the non-geodetic telescopes (except Onsala85) were estimated.

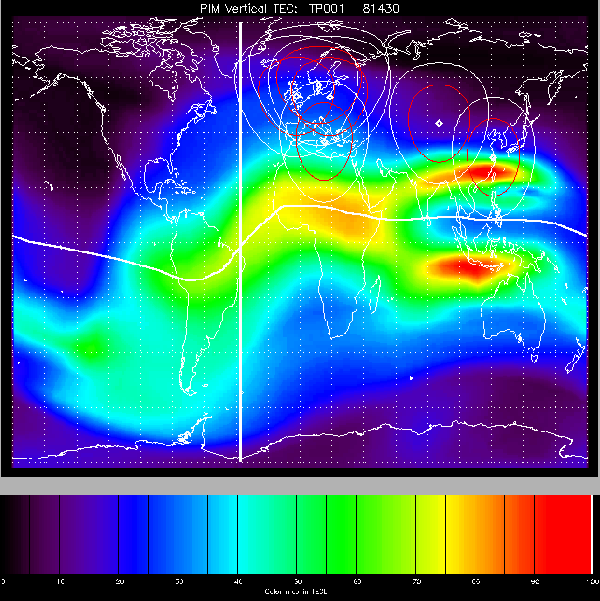
**Figure 1:** Global ionospheric map showing the vertical TEC calculated by PIM at 14:30 UT on November 23, 2000, with color scale in TEC units (1 TECU=10¹⁶electrons/m²). The thick vertical line indicates the longitude of the Sun, while the line orientated East-West represents the magnetic equator. ``Circles'' around selected stations show intersections of constant-elevation lines of sight (0° for white circles, 30° for red circles) with an altitude of 500 km, representing a maximal value for the height of the F₂-layer peak.

The troposphere was modeled using the Niell mapping function [6], estimating one zenith tropospheric delay per station for the whole 24-hour period with a priori values derived from meteorological measurements. This scheme differs from that used in standard geodetic experiments where new zenith troposperic delays are estimated at much shorter time intervals, but was preferred for this specific dataset to limit the number of estimated parameters. The ionosphere was modeled using the Parameterized Ionospheric Model (PIM), which is a theoretical model of ionospheric climatology developed at USAF Phillips Laboratory [7] and freely available. This model determines the electron density at a given point of the ionosphere (defined by latitude, longitude and height) as a function of local time, latitude, season, solar activity, geomagnetic activity, and interplanetary magnetic-field direction. Integration along a given direction then provides the total electron content (TEC), which serves as the basis to calculate the ionospheric delay. For our analysis, ionospheric delays were determined directly along the lines of sight between the stations/observed sources using a specific version of PIM developed for application to VLBI astrometry [8], and added afterwards to the ionospheric-free VLBI model implemented in MODEST. Figure 1 shows a global map of vertical TEC, representative of the ionospheric morphology at 14:30 UT on the day of our observations. Examination of similar maps at various times during the experiment revealed that the ionosphere was relatively stable over Europe on that day, but was significantly disturbed over the eastern part of China where the Shanghai telescope is located (see Fig. 1).

4 New telescope positions

Based on the above analysis and modeling, the post-fit rms residuals were 292 ps for delay with a χ² per degree of freedom of 1.03, and 230 fs/s for delay rate with a χ² per degree of freedom of 1.05. The data from two telescopes, Shanghai and Cambridge, have not been used in the analysis. All baselines to Shanghai showed larger residuals, most probably caused by ionospheric disturbances improperly modeled by PIM (see above). It was also decided to discard the observations from Cambridge because this telescope had usable data in only one frequency channel. This was, however, not a major inconvenience for the project, since the coordinates of Cambridge could be derived from those of Jodrell Bank by using estimates of the Cambridge-Jodrell Bank baseline, measured to a few centimeter accuracy from MERLIN observations of source pairs. Figure 2 shows the rms delay residuals as a function of baseline length with a least-squares linear fit to the data. There is a statistically-significant trend indicating an increase of the residuals with baseline length, which is expected if the ionosphere is the dominating error in the model. For short baselines, mismodeling is attenuated because ionospheric variations are correlated at nearby stations and partially cancel out when calculating the differential delay contribution.

**Figure 2:** Rms delay residuals (in ps) as a function of baseline length (excluding baselines to Shanghai).
$\includegraphics[bb=160 303 469 545,width=14cm,clip]{p197.ps}$

The estimated geodetic positions of Jodrell Bank, Torun, and Westerbork derived from this analysis, are given in Table 1 together with the shifts to the original coordinates (as previously available from the station catalog of the SCHED scheduling software). These shifts are listed for each telescope on the line immediately following its estimated coordinates. For completeness, the coordinates and shifts of the non-geodetic antenna Onsala85 are also listed, although these were not estimated in the analysis (see above). One notes that the corrections to the original coordinates of the four telescopes are as large as several meters. Uncertainties in the individual coordinates (one-sigma error derived from the least-squares fit) range from 1 to 3 cm, which is relatively small for such single-frequency observations. To determine whether these are realistic, alternate analyses estimating ``known'' parameters have been carried out, as described below.

**Table 1:** Coordinates of four EVN telescopes in ITRF2000 (epoch 1997.0) and shifts to original values.
Telescope	X (m)	Y (m)	Z (m)


Jodrell Bank	3822846.76 ± 0.02	–153802.28 ± 0.01	5086285.90 ± 0.02
Jodrell Bank	4.10 ± 0.02	–2.15 ± 0.01	–1.32 ± 0.02
Torun	3638558.51 ± 0.02	1221969.72 ± 0.01	5077036.76 ± 0.03
Torun	0.51 ± 0.02	2.72 ± 0.01	–4.24 ± 0.03
Westerbork	3828651.29 ± 0.02	443447.48 ± 0.01	5064921.57 ± 0.02
Westerbork	4.11 ± 0.02	–2.54 ± 0.01	–1.51 ± 0.02
Onsala85	3370966.126	711465.954	5349664.023
Onsala85	–2.055	1.037	–0.090

5 Assessment of accuracy

Validation of our analysis and results was first considered by estimating the coordinates of the geodetic telescopes. For this purpose, four alternate analyses, each estimating in turn the coordinates of one of the geodetic telescopes (including Onsala85) in addition to those of the non-geodetic telescopes, have been carried out. Results are given in Table 2 in terms of corrections to ITRF2000 coordinates. Since these coordinates are known to sub-centimeter accuracy, any significant correction would have to be attributed to deficiencies of our analysis. Table 2 shows that this is not the case since all estimated corrections are within one-sigma error. This is an indication that our derived uncertainties, although relatively small, are probably realistic.

**Table 2:** Estimated corrections to ITRF2000 coordinates of EVN telescopes at geodetic sites.
Telescope	ΔX (m)	ΔY (m)	ΔZ (m)


Effelsberg	0.00 ± 0.02	0.00 ± 0.01	–0.01 ± 0.03
Medicina	–0.02 ± 0.03	0.01 ± 0.01	0.03 ± 0.03
Noto	–0.01 ± 0.03	0.00 ± 0.01	–0.02 ± 0.02
Onsala85	0.00 ± 0.02	–0.01 ± 0.01	–0.03 ± 0.03

An additional test consisted in estimating the telescope axis offsets. Again, these should be known to centimeter accuracy and no significant deviations should be found. For this test, a single analysis estimating the axis offsets of all telescopes together with the coordinates of the non-geodetic telescopes, was performed. The axis offset corrections derived from this analysis are given in Table 3, also including antenna types and a priori values for completeness. The results in Table 3 show that the estimated corrections are not significant for six of the telescopes, confirming the previous indication that parameter uncertainties derived from our analysis appears to be realistic. For Jodrell Bank, however, a correction significant at the 3-sigma level ( –0.19 ± 0.06 m) is found. It is not yet understood whether this correction might be real or whether it is an artefact from our data. When estimating this parameter, the X and Z coordinates of Jodrell Bank shift by 15 to 20 cm, which is larger than the uncertainties given in Table 1. These coordinates are thus subject to caution (at such a level of accuracy) until the origin of the axis offset correction is understood.

**Table 3:** Antenna types, a priori axis offsets and estimated corrections.
Telescope	Antenna type	Axis offset (m)	Correction (m)


Effelsberg	AZEL	0.00	0.01 ± 0.02
Jodrell Bank	AZEL	0.458	–0.19 ± 0.06
Medicina	AZEL	1.83	–0.01 ± 0.03
Noto	AZEL	1.83	0.00 ± 0.02
Onsala85	EQU	2.15	0.01 ± 0.01
Torun	AZEL	0.00	–0.02 ± 0.06
Westerbork	EQU	4.95	0.02 ± 0.02

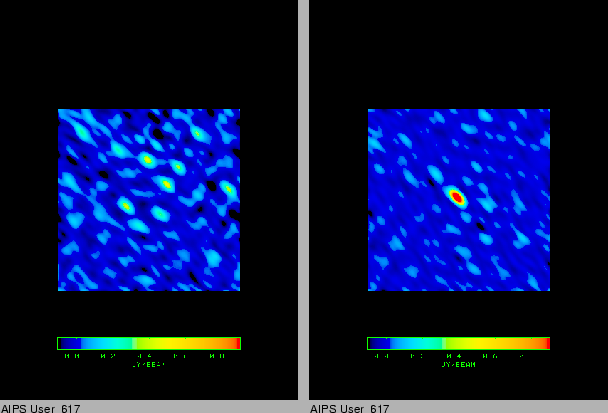
**Figure 3:** Phase-referenced maps of J1635+380 using 3C345 as phase calibrator. *Left:* image made using the original telescope coordinates. Peak flux is 0.49 Jy/beam. *Right:* image made using the newly-derived telescope coordinates in Table 1. Peak flux is 1.55 Jy/beam. Both images are plotted with the same color scale, ranging from –0.1 to 0.9 Jy/beam.

Finally, a qualitative evaluation of our results was accomplished by comparing phase-referenced maps made with the original and newly-derived telescope coordinates. For this comparison, we used data from a 6-cm phase-reference test experiment consisting of 1-hour of interleaved observations on the close pair 3C345/J1635+380 2.25°). Figure 3 shows the maps of J1635+3808 for the two cases. The problems with the phase-reference map using the original telescope positions are evident, as is the improvement in focusing the flux into the source and the reduction of the off-source noise when the newly-derived positions are used. This decisive test validates definitively our estimated telescope positions, and alternately demonstrates that phase-referencing can only be successful if an accurate geometrical VLBI model is available.

6 Conclusion

Based on a non-standard 5 GHz geodetic experiment conducted in November 2000, improved coordinates of three non-geodetic EVN telescopes have been obtained. These newly-derived positions are accurate to about 5 cm, a factor of 100 improvement over previous values. Such improved coordinates will be largely of benefit to VLBI observations with the EVN, especially those conducted with the phase-referencing technique. The new telescope positions, and others derived from these via local ties, have been made available to the EVN users and VLBI correlators that regularly process data from EVN telescopes. Further investigation will continue, in particular to determine the as-yet-unidentified origin of the Jodrell Bank axis offset correction, but also more generally to evaluate the influence of the ionosphere, troposphere and clock modeling on these results.

Acknowledgements

We are indebted to a number of people who have indirectly contributed to the success of this project. Nancy Vandenberg provided us with a version of SKED that can deal with single-frequency setups and made useful suggestions regarding the design of this experiment. Chris Jacobs, Chopo Ma and Dave Shaffer also helped in the initial stages of the experiment design, while Ed Himwich answered last-minute critical questions. The data were exported to a geodetic data base file with help from Arno Müskens and Izabela Rottmann. Special thanks are due to Richard Porcas for stimulating discussions and to Huib Jan van Langevelde for continued interest in this project. The observations and analysis presented in this report were carried out for the benefit of the EVN with support from the European Commission's IHP programme Access to Research Infrastructures under contract No. HPRI-CT-1999-00045.

ITRF2000Positions of Non-geodetic Telescopes in theEuropean VLBINetwork

1 Introduction

2 Experiment design and observations

3 Data analysis and modeling

4 New telescope positions

5 Assessment of accuracy

6 Conclusion

Acknowledgements

Bibliography

Footnotes

ITRF2000 Positions of Non-geodetic Telescopes in the European VLBI Network

Footnotes

ITRF2000Positions of Non-geodetic Telescopes in theEuropean VLBINetwork