Mat. V Kraj.
Symp. Nauk Rad. (URSI)
(Proc. V National Symp. Radio Science),
Toruń, 9–11.II.1987
(red. B. Krygier), Wyd. UMK,
Część I, s. 351–354 & Abstracts p. 86
Andrzej J. Maciejewski,
Kazimierz M. Borkowski*
Uniwersytet M. Kopernika
Instytut Astronomii
*Katedra
Radioastronomii
Toruń.
|
POWIERZCHNIA CIENIA NÓG WSPORCZYCH OŚWIETLACZY NA PŁASZCZYŹNIE APERTURY ANTEN PARABOLICZNYCH |
|
FEED SUPPORT BLOCKAGE AREA IN PARABOLIC ANTENNAS Abstract. Exact analytical solutions for calculating the shape and area of shadows cast by feed support legs which are oriented arbitrarily with respect to the main axis of parabolic antennas are presented. An example is given for the 32 m radiotelescope planned for the Toruń Radio Astronomy Observatory. A full account in English will be published elsewhere |
Jednym z czynników powodujących zmniejszenie wzmocnienia
anten parabolicznych jest przesłanianie odbieranego promieniowania
przez lustro wtórne i jego konstrukcję nośną. Wielkość strat
zależy w pierwszym rzędzie od konkretnego rozwiązania
radioteleskopu, funkcji oświetlenia apertury oraz częstotliwości
roboczej. Nie znamy żadnej teorii, która pozwalałaby na ścisłe
uwzględnienie tych strat [1]. W praktyce,
powierzchnię cienia znajduje się przez rzut graficzny, ważąc
ją funkcją oświetlenia. Procedura ta zawodzi, gdy wymiary
elementów przesłaniających są rzędu długości fali, gdyż wtedy
cień radiowy jest znacząco większy od cienia optycznego.
Jednakowoż, z wielu przyczyn rzutowanie optyczne jest bardzo
wygodne jako pierwsze przybliżenie.
Większość konstrukcji nośnych współczesnych radioteleskopów ma postać trój- lub czteronożnych podpór, których przedłużenia przecinają się nad ogniskiem pierwotnym radioteleskopu. Ruze [2] przedstawił stosunkowo proste wzory przybliżające pole cienia i straty wzmocnienia dla takich właśnie konstrukcji. Ostatnio pojawiły się konstrukcje z podporami ustawionymi skośnie względem osi paraboloidy. Jako przykład podajemy angielsko-holenderski teleskop 15 m na fale milimetrowe
 |
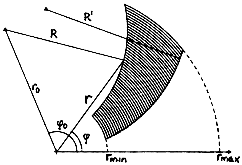
| Rys. 1. Schemat rzutu cienia ukośnej podpory na płaszczyznę apertury. Podpora umocowana jest w odległości rmin od osi parabolicznej czaszy. Rzut ograniczony jest czterema okręgami o promieniach: rmin, rmax, R = 2f/n3 i R' = 2f/n'3 |
Cień optyczny rzucany na płaszczyznę apertury składa się z trzech części [2]. Ograniczyliśmy się do analizy zewnętrznej części cienia, powstającego w wyniku przesłaniania przez podpory sferycznej fali skupianej w kierunku ogniska. Wpływ pozostałych składnik6w można uwzględnić prostymi metodami. Powierzchnia rozważanego przez nas cienia zależy od orientacji podpory względem osi paraboloidy, wymiarów liniowych podpór oraz długości ogniskowej i promienia czaszy teleskopu.
Rozważmy granice cienia rzucanego przez pojedynczą podporę (Rys. 1). Łatwo jest zauważyć, że wyznaczają je przekroje paraboloidy płaszczyznami stycznymi do podpory i przechodzęcymi przez ognisko pierwotne. Niech n oznacza wersor prostopadły do jednej z tych płaszczyzn (przyjmujemy, że n3 > 0). Wtedy na płaszczyźnie apertury we współrzędnych (x,y) o początku w ognisku równanie granicy cienia będzie miało postać
| (x + 2fn1/n3)2 + (y + 2fn2/n3)2 = (2f/n3)2. | (1) |
Jest to równanie okręgu, które we współrzędnych biegunowych można zapisać jako:
| φ(r) = φo – sign(φo) arccos[(r2 – 4f2)/(2 r ro)] | (2) |
lub
| (3) |
|
| (4) |
gdzie f(r) jest funkcją oświetlenia, a rmin — odległością punktu przebicia osi podpory z powierzchnią paraboloidy. Dla prostszych postaci f(r) wielkość (4) można obliczyć analitycznie, jednakże rozwiązania zawierają niewygodne całki eliptyczne. Niemniej, wzór ten jest bardzo użyteczny do zwykłego całkowania numerycznego. Powierzchnia efektywna cienia (4) może być obliczona również w oparciu o parametryzację (3). Po dokładnej analizie okazało się, że końcowy wynik ma postać elementarną. Pomijając szczegóły długich wyliczeń, ostatecznie można dojść do następującego rozwiązania.
Oznaczamy
| U(α,g) = {g P(α,g) + sin[P(α,g)]} 4f2/(g – 1/g), | (5) |
| P(α,g) = α + arcsin[sin(α)/g], | (6) |
wtedy powierzchnia cienia rzutowanego na płaszczyznę apertury (gdy f(r) = 1) wynosi
|
| + U(φ1 – φo',g) + U(φ2' – φo',g') – U(φ1' – φo',g')], | (7) |
gdzie, φ2 = φ(rmax), φ1 = φ(rmin). Przyjmując dość typową funkcję oświetlenia postaci f(r) = 1 – a(r/rmax)2 powierzchnię efektywną określamy jako:
|
| – D(φ2 – φo,g) + D(φ1 – φo,g) + D(φ2' – φo',g') – D(φ1' – φo',g')], | (8) |
|
D(α,g)
= {(g2 + 2)P(α,g)
+ [3g + 1/g + cos(P(α,g))]× ×sin(P(α,g))}(2f)4/(g – 1/g)2. | (9) |
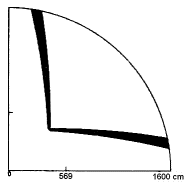 |
| Rys. 2. Zewnętrzna część cienia podpór 32 m toruńskiego radioteleskopu. Na rysunku zachowano skalę. Obszar zakreskowany ma powierzchnię 11,28 m2. |
Wzory (5) – (9) stanowią ścisłe rozwiązanie problemu wyznaczania powierzchni cienia rzucanego przez skośnie ustawione podpory.
Praktyczne testy przeprowadziliśmy na przykładzie projektu toruńskiego radioteleskopu o średnicy czaszy 32 m i ogniskowej 11.2 m. Jego konstrukcja nośna subreflektora składa się z ośmiu cylindrycznych podpór, każda o średnicy 0,159 m i które są zorientowane tak, że ich cienie mają jednakową powierzchnię i są przystających kształtów. Cień rzucany przez jedną podporę, rzutowany na płaszczyznę apertury i obliczony zgodnie z (7) wynosi 5.64 m2, co stanowi 6.42 % jednej ósmej powierzchni apertury na zewnątrz koła o promieniu rmin = 5.6869 m. Jego kształt przedstawia Rys. 2. Dla typowej wartości a = 0.75 względne straty powierzchni są nieznacznie mniejsze (6.31 %). Bliższe dane oraz program pozwalająoy wyliczać efektywną powierzchnię cienia można znaleźć w pracy autorów [3].
LITERATURA
1. Rusch W.V.T., Analysis of Paraboloidal — Reflector Systems, Methods of Experimental Physics, 12B, 29 (1976).
2. Ruze J., Feed Support Blockage Loss in Parabolic Antennas, Microwave J., 11, 12, 76 (1968).
3. Borkowski K.M., Maciejewski A.J., Feed Support Blockage Area in Parabolic Antennas, submitted to Scienific Instrumentation [2, 2, 69–75 (1987)].