Mat. V Kraj.
Symp. Nauk Rad. (URSI)
(Proc. V National Symp. Radio Science),
Toruń, 9–11.II.1987
(red. B. Krygier), Wyd. UMK,
Część I, s. 337–342 & Abstracts p. 76
Kazimierz M. Borkowski
Uniwersytet M. Kopernika
Katedra
Radioastronomii
Toruń.
| OKOŁOZENITALNE OGRANICZENIA OBSERWACJI ASTRONOMICZNYCH DLA TELESKOPÓW O MONTAŻU HORYZONTALNYM |
|
CIRCUMZENITHAL LlMITS FOR ASTRONOMICAL OBSERVATIONS WITH TELESCOPES OF THE ALT–AZ MOUNTING Abstract. All telescopes mounted in the horizon system of coordinates are unable to follow the usual diurnal motion of heavenly bodies in a small region around the zenith. The "blind spot" is normally exclusively due to the limits on maximum usable speed and acceleration of the telescope around the azimuth axis. The azimuth speed of the sky is maximum at the local meridian: A'max = cosδ / sin(φ – δ) in rad/rad or in degrees per 4 sidereal minutes, where φ is the geographical latitude and δ — the declination. For a telescope whose maximum azimuth drive speed is V the spot has the extent equal to arctg[2V cosφ / (V2 – 1)] in declination and at least π/V in the E-W direction (in the hour angle, t). The E-W size (slightly) and shape (strongly) depend on the strategy of driving the telescope through the spot. Arranging the driving to produce the symmetrical spot about the meridian allows one to describe its contour with a simple equation:
|
Ruchy teleskopu zmontowanego w układzie horyzontalnym odbywają
się wokól dwóch wzajemnie prostopadłych osi: pionowej (osi
azymutu) i poziomej (osi wysokości albo kąta elewacji). Ponieważ
sfera niebleska obraca się wokół osi świata, tj. osi obrotu
Ziemi, nie pokrywającej się z żadną z wymienionych dwóch osi
teleskopu, istnieje punkt osobliwy na sferze niebieskiej
(zenit), w którym prędkości i przyśpieszenia zmian azymutu
obiektów astronomicznych osiągają nieskończoną wartość. Ponadto,
w niewielkim otoczeniu zenitu prędkości chociaż skończone, zawsze
przekraczają techniczne możliwości rzeczywistych teleskopów.
Bliższa analiza pokazuje także, że niekiedy ograniczenia
na możliwości prowadzenia obserwacji mogą również dotyczyć sterowania
w osi wysokości oraz kącie paralaktycznym, lecz te w
praktyce na ogół nie są krytyczne, dlatego ograniczę się tutaj
jedynie do osi azymutalnej. Pełniejszą dyskusję tego problemu
przedstawiono w pracach [1] i [2].
Prędkość zmiany azymutu A obiektów poruszających się ruchem dobowym na sferze niebieskiej wyraża się wzorem
| (1) |
gdzie φ jest szerokością geograficzną miejsca obserwacji, δ — deklinacją obiektu, zaś z — odległością zenitalną (dopełnieniem do π/2 kąta elewacji). Ze wzoru (1) wynika, że najszybsze zmiany azymutu towarzyszą przejściom obiektów przez południk miejscowy, na którym kąt godzinny, t, jest zerowy, a azymut przyjmuje wartość 0 lub π:
| A'max = cosδ/sin(φ – δ) . | (2) |
Wzór (2) pozwala ocenić w jakim zakresie deklinacji A'max przewyższa maksymalną dopuszczalną prędkość ruchu teleskopu w osi azymutu, V. Po nieskomplikowanych przekształceniach dostaje się następujące wzory na granice tego zakresu:
| (3) |
gdzie V jest wyrażone w jednostkach naturalnych, tzn. w rad/rad albo (obrotach teleskopu)/(obrót nieba). We wzorze tym znak plus należy wybrać dla obiektów górujących po południowej stronie nieba (gdzie A' > 0, zatem maksymalna szybkość teleskopu wynosi V), zaś znak minus — po stronie północnej (ujemne prędkości azymutalne, –V). Szerokość pasa na niebie, w którym obiekty w pobliżu swego górowania poruszają się szybciej niż V wynosi więc
| (4) |
Na przykład, dla szerokości Torunia (φ = 53,1°) i prędkości teleskopu V = 120 = 30°/min., δ– – δ+ = 34,4'.
Posługując się wzorem (1) można pokazać, że całkowicie niedostępny dla obserwacji typu śledzenia obiektów niebieskich obszar składa się z dwóch owali stycznych do siebie w zenicie ze środkami na południku miejscowym (Rys. 1), które na płaszczyźnie (t cosδ, δ) z dobrym przybliżeniem są okręgami o średnicach D± = cosφ/(±V – sinφ). Ich kontury opisuje ściśle
| tg z = D±cos A. | (5) |
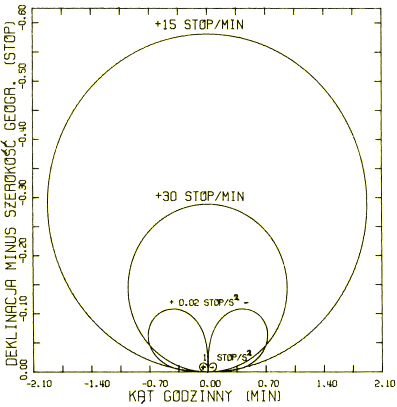
 |
| Rys. 1. Krzywe jednakowych prędkości i przyśpieszeń azymutalnych sfery niebieskiej na południowej stronie zenitu na szerokości geograficznej 53,1°. Krzywe północnej strony, chociaż obejmują nieznacznie mniejszy obszar, są niemal lustrzanym odbiciem, tych wyrysowanych, wokół dolnego obramowania rysunku, z tym że znaki prędkości i przyśpieszeń są tam przeciwne. Wszędzie wewnątrz tych konturów odpowiednie prędkości i przyśpieszenia są w wartościach bezwzględnych większe niż na zewnątrz. |
Kąt godzinny, przy którym teleskop śledzący obiekt z krytyczną deklinacją po wschodniej stronie południka przestanie za nim nadążać, można obliczyć w sposób elementarny ściśle [1], jednak praktyczniej jest posłużyć się prostszym przybliżeniem:
| to ≈ – √[(φ – δ)(δ – φ + Δ±)]/cosδ ≈ –√[(φ – δ)(δ – δ±)]/cosδ. | (6) |
Kątowi temu można przypisać azymut
| Ao ≈ –arccos√[(φ – δ)/D±]. | (7) |
Przybliżenia (6) i (7) nadają się wprost do oceny czasu przejścia obiektu (–2to) i teleskopu (–2Ao) przez ,,ślepy" obszar. Warto tu zauważyć, że dla obiektów górujących w zenicie Ao = –π/2, a zatem — pomimo, że to = 0 — teleskop będzie doganiał obiekt najdłużej. W pierwszym przybliżeniu czas martwego ruchu teleskopu przez zenit wyniesie π/V rad, albo, przy V = 120, 12·60/120 min. = 6 min. Oczywiście, gdy teleskop przebywa drogę –2Ao, obiekt przesunie się nieco dalej. Ścisłe wyznaczenie czasu doganiania wymaga rozwiązania równania tranacendentalnego. Można pokazać [1], że takie rozwiązanie jest optymalnym, tzn. prowadzącym do najmniejszych strat czasowych.
Z pewnych względów uzasadnione może się okazać przyjęcie innej niż ta optymalna strategii obserwacji. Można, na przykład, nie śledzić obiektu aż do samej granicy ślepego obszaru lecz przyśpieszyć teleskop w azymucie nieco wcześniej — tak, by w chwili tranzytu (przejścia przez południk) obserwowany obiekt dogonił teleskop. Oczywiście, obiekt ma w tym miejscu znacznie większą prędkość niż teleskop, ale ten ostatni posuwając się stale z tą samą maksymalną prędkością dogoni obiekt po zachodniej stronie nieba w punkcie dokładnie symetrycznym względem miejsca ucieczki przed ślepą plamą. Przy takiej procedurze powstaje symetryczny martwy obszar, którego kontur ściśle opisuje
|
(8) |
Czytelnik może sprawdzić, że maksymalne rozmiary tego obszaru są zgodne ze wzorami (3) lub (4) w deklinacji i π/V w kącie godzinnym (wszakże nie w zenicie, lecz na deklinacji wynoszącej arctg[tgφ cos[π/(2V)], gdzie kontur ,,+", południowy, przecina kontur ,,–", północny). Owe π/V wymaga jednak używania ujemnych prędkości teleskopu (–V) na południowej stronie nieba (tzn. kątów elewacji większych od 90°) i chociaż jest to na ogół możliwe, jednak z pewnością jest niewygodne, dlatego obszar opisany równaniem (8) będzie miał w praktyce nieciągłość przy δ = φ i rozciągłość w kącie godzinnym nieco większą niż ta teoretycznie możliwa, około π/(V – 2/sinφ).
Zaletą symetrycznej ślepej plamy jest to, że w praktyce pokrywa ona wszystkie pozostałe obszary niewydolności teleskopów, zaś do wad zaliczyć wypada złożony system sterowania. Przyjmując konwencję zliczania azymutu i kąta godzinnego od południka miejscowego na zachód w zakresie od 0 do 2π można zasugerować następujący względnie prosty algorytm dla programu sterującego: Jeśli deklinacja obserwowanego obiektu spełnia warunek δ+ < d < δ–, a ponadto t > 3π/2 oraz t – 1,5π ≥ (A – 1,5π)/±V (gdzie znak V trzeba wybrać zgodnie z aktualną prędkością teleskopu i obiektu), to należy z maksymlną prędkością przestawić teleskop na pozycję znowe = z i Anowe = 2π – A, po czym kontynuować śledzenie.
Są takie miejsca na niebie, w których teleskop przestanie nadążać za śledzonym obiektem nie z powodu ograniczonej szybkości, lecz przyśpieszenia. W bliskim sąsiedztwie zenitu słuszne jest przybliżenie
| A" ≈ –2·(A')2, | (9) |
a kontur jednakowych przyśpieszeń, A" = a, dany jest równaniem
| (10) |
Krzywa ta przecina kontur jednakowych prędkości (5) lub (6) w punktach o współrzędnych
| (11a) |
| (11b) |
Pomiędzy deklinacjami δ* ze wzoru (11a) przyśpieszenie teleskopu będzie ograniczało obszar efektywnych obserwacji astronomicznych. W praktyce jest to jednak tylko teoretyczne ograniczenie. Na przykład, przyśpieszenie toruńskiego teleskopu rzędu 1 °/s2 (a = 3,3·106 rad/rad2) oznacza t* = ±1 s i δ* = φ ± 0,078", co oczywiście jest zaniedbywalnie małym obszarem.
LITERATURA:
[1] K.M. Borkowski, 1986, Acta Astron. (w druku)
[37 (1987), 79–88].
[2] F.G. Watson,1978, M.N.R.A.S. 183, 277.