 |
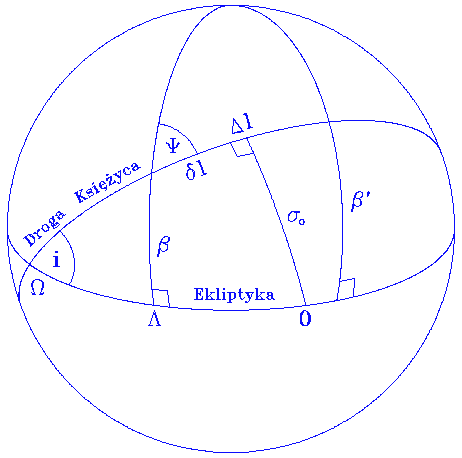
Ryc. 1.
Toruń —
Katedra Radioastronomii UMK
Zaćmienia Słońca i Księżyca
Wielki epos staroindyjski Mahabharata (też Ramajana i kilka puran) tak opisuje genezę zaćmień Słońca i Księżyca: Upragnioną amritę, tj. napój nieśmiertelności, bogowie i asurowie (demony) otrzymali po długotrwałym wspólnym ubijaniu oceanu. Podstępni bogowie zagarnęli jednak ów napój wyłącznie dla siebie przy pomocy fortelu. Kiedy tak się nim raczyli jeden z asurów — smok Rahu (w literaturze wedyjskiej Swarbhanu) — przybrawszy postać boga ukradkiem dołączył do grupy pijących. Szybko jednak rozpoznało go Słońce i Księżyc, a ponieważ dobrze życzyli bogom więc zdemaskowali smoka. Rozgniewany Wisznu odciął smokowi głowę w chwili, gdy ten już rozpoczął picie amrity jednak nie zdążył jeszcze przełknąć pierwszej porcji. W efekcie tego zbiegu okoliczności odcięta głowa Rahu stając się nieśmiertelna wzniosła się do nieba, a reszta śmiertelnego ciała, jak powiadają, runęła w dół aż ziemia zadrżała od upadku. Od tamtej pory Rahu pozostaje na niebie i żywiąc niepohamowaną nienawiść do Słońca i Księżyca prześladuje je nieustannie. Chcąc zemścić się za zdemaskowanie co jakiś czas usiłuje je połknąć, a efektem tych prób są zaćmienia (Erman i Tiomkin, 1987).
W kontraście do powyższego opisu, dzisiejsi astronomowie pojmują te zjawiska zgoła prozaicznie: oto Księżyc w swej comiesięcznej wędrówce wokół Ziemi, gdy znajdzie się na kierunku Słońce — Ziemia przesłania Słońce (w okresie nowiu) bądź zagłębia się w cień Ziemi (w czasie pełni). Nie każdemu obiegowi Księżyca towarzyszą jednak zaćmienia, gdyż orbita naszego naturalnego satelity jest nachylona do płaszczyzny ekliptyki (drogi Słońca na tle gwiazd) pod kątem o rząd większym od widomych tarcz Słońca i Księżyca i kilkakrotnie większym od cienia Ziemi w odległości Księżyca. Jeśli spotkanie (konjunkcja) Księżyca ze Słońcem lub cieniem Ziemi następuje dostatecznie blisko węzłów orbity Księżyca (punktów przebicia płaszczyzny ekliptyki przez orbitę) to niezawodnie mamy zjawisko zaćmienia. Teoria astronomiczna ma tą istotną przewagę nad wedyjską, że pozwala m.in. na dość precyzyjne przewidywanie występowania zaćmień już od czasów starożytności i hen w odległą przyszłość. Tak np., bliższa analiza geometrii zaćmień prowadzi do wniosku, że w ciągu roku musi wystąpić przynajmniej dwa zaćmienia (wtedy oba są słoneczne), a może ich być nawet siedem (4 słoneczne i 3 księżycowe lub 5 słonecznych i 2 księżycowe). Średnio na jedno stulecie przypada około 237 zaćmień Słońca i 154 zaćmienia Księżyca (w tym 71 całkowitych).
Zaćmienia Słońca — zwłaszcza centralne, przy których dysk słoneczny zostaje całkowicie przesłonięty przez Księżyc (zaćmienie całkowite) lub tarcza Księżyca znajdzie się całym obwodem wewnątrz dysku słonecznego (zaćmienie obrączkowe) — należą do najbardziej widowiskowych zjawisk przyrody. Podczas całkowitego zaćmienia w pełni dnia dość nagle na kilka minut (do 7m31s) zapada prawdziwy zmrok, a przy tym zwierzęta reagują niespokojem, ptactwo udaje się na spoczynek, a na niebie pojawiają się planety i najjaśniejsze gwiazdy. Niestety, są to jednak nadzwyczaj rzadkie zjawiska. W określonym miejscu tylko raz na kilkaset lat występuje całkowite zaćmienie Słońca. Dzieje się tak ponieważ cień rzucany przez Księżyc przy powierzchni Ziemi osiąga średnicę co najwyżej kilkuset kilometrów (ściślej: do 270) i chociaż plama taka wędruje tysiące kilometrów (z szybkością pół kilometra na sekundę generalnie ku wschodowi) to zakreślony pas (całkowitego zaćmienia) stanowi zwykle znacznie mniej niż jeden procent powierzchni Ziemi. Dla obserwatorów poza tym pasem zaćmienie — jeśli w ogóle ma miejsce — jawi się tylko częściowym. Ciekawe, że nawet gdy faza zaćmienia częściowego jest względnie duża (sięgająca 98 % przesłoniętej średnicy Słońca, Stephenson i Clark 1978), przy bezchmurnej pogodzie nieprzygotowany obserwator może wcale nie zauważyć zjawiska, gdyż ubytek w jasności otoczenia nie jest alarmująco duży. Z drugiej strony, w pewnych sytuacjach (sprzyjające zachmurzenie lub mgła) zaćmienia nawet o bardzo małej fazie łatwo dają się obserwować.
W odróżnieniu od zaćmień Słońca zaćmienia Księżyca są widoczne na całej półkuli Ziemi, której biegunem jest punkt podksiężycowy (Księżyc jest w zenicie nad tym punktem). Mimo, że pod względem widowiskowości ustępują wyraźnie słonecznym, zaćmienia te są także zjawiskami o wyjątkowym uroku. Oto jeszcze na krótko przed zaćmieniem na niebie obficie okraszonym blaskiem pełni Księżyca widoczne pozostają jedynie najjaśniejsze gwiazdy. W miarę pogrążania się globu księżycowego w cieniu rzucanym przez Ziemię coraz więcej gwiazd pojawia się na niebie. Wreszcie, w czasie pełnej fazy, która może trwać dobrze ponad godzinę (1h40m), niebo znów zapełnia miriady gwiazd. Naturalnie nie wszystkie zaćmienia są całkowitymi. Częściej bywa, że Księżyc tylko muśnie stożek cienia Ziemi i pomknie dalej w swej wędrówce wokół Ziemi. Mówimy wtedy o częściowym zaćmieniu.
Współczesne i historyczne obserwacje zaćmień Słońca i Księżyca, a zwłaszcza zaćmień całkowitych, stanowią unikalne źródło wiedzy o samym Słońcu (np. Sofia i in. 1980), ruchu Księżyca (np. Zawilski 1989) i rotacji Ziemi (np. Borkowski 1988, Pang i in. 1988, Stephenson i Said 1989). Dla historyków stanowią one bezcenną, niekiedy jedyną, informację o datach przeszłych zdarzeń (np. Pang 1987, de Jong i van Soldt 1989). Szczegółową i wyczerpującą dyskusję znaczenia historycznych zapisków obserwacji zaćmień przedstawił Zawilski (1989) w serii artykułów zamieszczonych w Uranii dlatego tutaj nie będziemy tego aspektu rozszerzać.
Istnieje jeszcze trzeci typ zaćmień, nazywanych półcieniowymi, kiedy tarczę Księżyca pokrywa częściowo (rzadziej całkowicie, Meeus 1980) tylko półcień Ziemi. Ten rodzaj zaćmień powszechnie umyka uwadze przygodnych obserwatorów, gdyż osłabienie blasku Księżyca jest w czasie tego zjawiska rzeczywiście niewielkie. Niemniej, również takie zaćmienie może być dość łatwo zaobserwowane nieuzbrojonym okiem jeśli jego faza (ułamek średnicy tarczy Księżyca pokryty półcieniem) przewyższy ok. 0,7 – 0,8 (Sharonov 1952). Obserwacje zaćmień półcieniowych są użyteczne w badaniach rozkładu natężenia światła wewnątrz stożka cienia, który niesie informacje o wyższych warstwach atmosfery Ziemi. W okresie 100 lat mamy średnio około 89 zaćmień półcieniowych. Jeśli w rachunkach uwzględnimy zaćmienia półcieniowe to w roku musi wystąpić przynajmniej 4 zaćmienia: po dwa słoneczne i księżycowe. Maksymalna liczba pozostaje 7, z tym że mogą to być także 2 zaćmienia Słońca i 5 Księżyca lub 3 Słońca i 4 Księżyca (Polozova 1955).
Wprawdzie literatura światowa zawiera bogaty zestaw spisów zaćmień (tzw. kanonów) od czasów historycznych po daleką przyszłość (np. Oppolzer 1887, Mucke i Meeus 1983, Meeus i Mucke 1983, Liu 1983, Stephenson i Houlden 1986, Espenak 1987) w naszym kraju są to publikacje trudnodostępne lub w ogóle nieosiągalne. Do niedawna mieliśmy praktycznie całkowity brak wyczerpujących opracowań dla terenu Polski, szczególnie jeśli chodzi o zaćmienia historyczne. Luki tej nie niwelował wyciąg z Oppolzera (1887) dla XX w. zamieszczony w kalendarzu Janiczka (1962). Cennym wkładem są natomiast niedawne prace Fangora (1990ab) obejmujące lata 1991 – 2200. W tej sytuacji postanowiłem przygotować listy zaćmień Słońca i Księżyca dla Polski dla całej historii naszego kraju w oparciu o własny program, napisany w języku FORTRAN77. Opis tego programu oraz szczegółowe wyniki obliczeń przedstawiłem w pracach Borkowski (1989, 1990a, 1990b). Tutaj podam tylko informacje najistotniejsze (jednak ze szczegółami nowego algorytmu dla zaćmień Księżyca) i niewielką porcję wyników dotyczących ,,polskich" zaćmień w najbliższych kilkudziesięciu latach.
Wspomniany program do obliczania okoliczności zaćmień jest dość
złożony (część kompilowalna zajmuje w pamięci komputera około 50 000
bajtów). Może on dostarczyć
listę zaćmień (jednego z trzech typów) dla zadanego miejsca (lub
kilkunastu miejsc jednocześnie) w zadanym okresie, obliczyć
okoliczności tylko najbliższego zaćmienia albo prześledzić
przebieg zaćmienia z zadanym krokiem (z dodatkową możliwością
graficznego przedstawienia na ekranie PC). Zasadniczym elementem
programu są procedury obliczania pozycji Słońca i Księżyca na
wybrany moment czasu dynamicznego (DT, dawniej znanego jako czas
efemeryd). Wykorzystuje się tutaj algorytmy
dające położenie tych dwóch ciał z dokładnością 2" (opisane są
w pracach: Bretagnon i in. 1986 oraz Chapront-Touze i Chapront 1988).
Oryginalne algorytmy nieco zmodyfikowałem, tak by uwzględnić
nutację i móc dobierać wiekowe pływowe przyspieszenie Księżyca
(standartowo –26 "/wiek/wiek). Wartości DT – UT, używane
do modyfikacji długości geograficznej i zamiany czasu dynamicznego
na uniwersalny (UT), są obliczane zgodnie z opracowaniem
Stephensona i Morrisona (1984). Dla prezentowanych tu wyników po
roku 1990 używam wzoru (w s):
| (1) |
W celu wygenerowania listy zaćmień mój program przeszukuje wszystkie opozycje lub konjunkcje (w długości ekliptycznej) Słońca z Księżycem, poczynając od podanej daty. Kiedy szerokość ekliptyczna w analizowanym momencie jest mniejsza od z góry zadanej wartości (innej dla zaćmień Słońca i Księżyca) wówczas przeprowadzana jest szczegółowa analiza możliwego zaćmienia i badanie czy będzie ono widoczne z określonego miejsca.
Dla zaćmień Słońca analiza ta przeprowadzana jest bezpośrednio na współrzędnych topocentrycznych, a nie — jak to się zwykle robi (np. Explanatory Supplement AENA 1961) — poprzez elementy Bessela. W tym celu w cyklicznym procesie zawężającym przedział czasu w okolicy maksimum fazy do około 4 minut wyznacza się moment maksymalnej fazy przez dopasowanie paraboli do odległości środków tarcz Słońca i Księżyca w trzech punktach na tym przedziale. Następnie, w innym procesie iteracyjnym (metoda Newtona) wyznaczane są momenty kontaktów (zrównanie odległości z sumą promieni tarcz).
W przypadku zaćmień Księżyca (cieniowych i półcieniowych) podobna analiza wykonywana jest także w oryginalny sposób. Ponieważ okazało się, że w istocie będąc prostą jest zarazem bardzo dokładną metodą nie wymagającą żadnych iteracji pozwolę sobie ją tutaj bliżej omówić.
Po wykryciu możliwości zaistnienia zaćmienia Księżyca oblicza
się kątową odległość tego ciała od kierunku środka cienia Ziemi co
pozwala na zgrubną ocenę czasu trwania zaćmienia [korzysta się tu
ze wzoru typu (8) niżej]. Następnie oblicza się współrzędne ekliptyczne
(szerokość β i długość L) dla dwóch momentów (DT i DT'
położonych symetrycznie względem momentu opozycji) odległych o
oceniony czas trwania (jednak nie mniej niż o jedną godzinę).
Dalsze rachunki przeprowadzane są w układzie współrzędnych:
szerokość — różnicowa długość ekliptyczna (ta druga współrzędna,
oznaczmy ją przez Λ, jest różnicą aktualnej długości i długości
środka cienia). Momenty maksymalnej fazy DTo i kontaktów cienia
lub półcienia z brzegiem dysku księżycowego: początek albo tzw.
drugi kontakt (DTo – t/2) i koniec zaćmienia albo tzw. trzeci
kontakt (DTo + t/2), są teraz obliczane w sposób ścisły. Dwa
położenia Księżyca względem cienia, (Λ,β) i
(Λ',β'), określają jednoznacznie chwilową ,,orbitę"
Księżyca (Ryc. 1), którą opisuje inklinacja względem ekliptyki
oraz długość (różnicowa) węzła wstępującego:
| Ryc. 1. |
| (2) |
| (3) |
| (4) |
| (5) |
| (6) |
| (7) |
| (8) |
Na zakończenie procedury oblicza się na nowo współrzędne równikowe Księżyca i cienia dla znalezionych trzech momentów, DTo ± t/2 oraz DTo, w celu obliczenia lokalnych okoliczności zaćmienia, tj. współrzędnych horyzontalnych Księżyca i położenia środka cienia względem środka Księżyca (kąta V mierzonego w lewo od kierunku na zenit). Naturalnie, trzeba tu uwzględnić paralaksę dobową i refrakcję atmosferyczną (do oceny tego ostatniego efektu użyłem formuł zaadaptowanych z Almanac for Computers 1988).
Liniową fazę zaćmienia definiuje się jako zaciemniony ułamek
średnicy D tarczy ciała ulegającego zaćmieniu:
| (9) |
| (10) |
| (11) |
| (12) |
Po wielu testach wykorzystałem opisany program (w wersji z początku 1988 r., kiedy opierał się on jeszcze — jak to obecnie oceniam — na niezbyt udanym algorytmie wyznaczania momentów kontaktów) do obliczenia okoliczności wszystkich zaćmień Słońca widocznych z 10 miast Polski (Warszawa, Toruń, Gdańsk, Szczecin, Poznań, Wrocław, Kraków, Lwów, Pińsk i Wilno) w latach 900 – 2200 (Borkowski 1989). Podobnie postąpiłem z cieniowymi zaćmieniami Księżyca widocznymi z obszaru Europy w tym samym zakresie czasu (Borkowski 1990a). Kolekcję zaćmień Słońca i Księżyca uzupełniłem jeszcze listą wszystkich zaćmień półcieniowych w okresie 300 lat (1900 – 2200; Borkowski 1990b). Dla celów niniejszej prezentacji wykonałem osobne obliczenia, z najwyższą dokładnością na jaką obecnie mój program pozwala, dla geograficznego położenia Warszawy (przyjmując długość geograficzną 21.03°E i szerokość 52.22°N) i w okresie nadchodzącego pół wieku (do 2040 r. włącznie). Te właśnie wyniki zawierają tabele 1 (zaćmienia Słońca), 2 (cieniowe Księżyca) i 3 (półcieniowe Księżyca). Odpowiednio do tabel, rysunki 2, 3 i 4 przedstawiają wygląd Słońca lub Księżyca w czasie maksymalnej fazy zaćmień częściowych (dla oszczędności miejsca w reprezentacji graficznej pominięto trywialny przypadek całkowitych zaćmień Księżyca).
W każdej ze wspomnianych tabel jednemu zaćmieniu odpowiada jeden wiersz rozpoczynający się od daty (rok, miesiąc i dzień miesiąca). W dalszych kolumnach podano momenty kontaktów (początek i koniec zaćmienia) i/lub maksymalnej fazy w czasie środkowo-europejskim (CSE — zimowym w Polsce tj. UT zwiększonym o 1 godz.) i odpowiadające wysokości ciała zaćmiewanego nad warszawskim horyzontem (h, w stopniach) oraz kąt pozycyjny V (też w stopniach). Niektóre momenty są wyrażone godziną przewyższającą 24 co należy interpretować jako odnoszące się do następnego dnia. Dla chwili maksymalnej fazy w tabelach podano ponadto (odpowiednio do rodzaju zaćmienia) azymut Słońca lub Księżyca (a, w stopniach), wartość fazy liniowej i powierzchniowej (F, w procentach) oraz kątowe rozmiary (średnice) dysków Słońca (Ds), Księżyca (Dm), cienia (Du) i półcienia (Dp) Ziemi w odległości Księżyca, wszystkie w minutach łuku. Ostatnia kolumna tabel zaćmień Księżyca zawiera moment (CSE) wschodu lub zachodu Księżyca w Warszawie, który jest najbliższy danemu zaćmieniu.
W przypadku zaćmień Słońca których teoretyczne maksimum
przypada pod horyzontem Warszawy, tabelaryczne maksimum fazy
odpowiada momentowi wschodu lub zachodu Słońca (chwile wschodów i
zachodów Słońca obliczono przy założeniu, że dolny skraj widomej
jego tarczy znajduje się na horyzoncie; podobnie zdefiniowane są
wschody i zachody Księżyca w Tab. 2 i 3).
Roczniki astronomiczne zwykle podają także momenty kontaktów
półcienia Ziemi z tarczą Księżyca w przypadku zaćmień cieniowych.
Wielkości te można odzyskać z Tab. 2 w następujący sposób: Z
danych tej tabeli obliczamy σo za pomocą odpowiednio
przekształconego wzoru (9) oraz czas t trwania zaćmienia z różnicy
jego momentów końca i początku. Wtedy czas upływający od wejścia
Księżyca w półcień przed zaćmieniem cieniowym do wyjścia z
półcienia po zaćmieniu wynosi
Dla zaćmień półcieniowych (Tab. 3) zamiast momentów kontaktów
podano czasy trwania zaćmienia t (w minutach czasu), a dla całkowitych także
czas trwania pełnej fazy T (też w minutach) w kolumnie (i zamiast) fazy
powierzchniowej F (równej wtedy ściśle 100%). Podobnie jak w
sugerowanych wyżej obliczeniach, momenty kontaktów dostaje się z
momentu środka zaćmienia przez dodanie i odjęcie połowy czasu
trwania danej fazy (t/2 albo T/2).
Inaczej niż dla Słońca, tabele 2 i 3 nie podają fazy w chwili
zachodu lub wschodu Księżyca podczas zaćmienia. Można ją obliczyć
ze wzoru (9) podstawiając tam zamiast σo
wartość arccos(cosσocost), gdzie τ = 2t'/t arccos{cos[(Dm + Du)/2]/cosσo}, a
t' jest czasem upływającym między środkiem zaćmienia i
interesującym nas momentem pamiętając dodatkowo, że dla zaćmień
półcieniowych w wyrażeniu na τ bierzemy tabelaryczne Dp zamiast
Du. Jeśli zadowoli nas mniejsza dokładność, to możemy τ (w
stopniach) ocenić na t'/118, gdy t' wyrazimy w minutach czasu.
Np., zaćmienie cieniowe z dnia 1993.11.29 ma środek około 7 minut
po zachodzie Księżyca w Warszawie. Obliczamy, że maksymalnej fazie
1,091 odpowiada σo = 22,11', a τ = 3,32', zatem faza przy
zachodzie wynosi 1,083 (posługując się uproszczonym rachunkiem
dostalibyśmy 1,082 przy τ = 3,56').
Z Tab. 1 i Ryc. 2 (por. też: Borkowski 1989, Fangor 1988,
Wiland i Zawilski 1986) wynika, że w najbliższych latach nie
będziemy w Polsce oglądać żadnego centralnego zaćmienia Słońca.
W istocie będzie tak aż do roku 2075, kiedy to wystąpi obrączkowe
zaćmienie widoczne m.in. z Krakowa, lecz Warszawa będzie musiała
poczekać na podobną okazję ponad 200 lat — do 2195 r. (wspomnieć
warto, że ostatnio Warszawa była świadkiem centralnego zaćmienia
28 lipca 1851 r., a było ono całkowitym).
Dla odmiany, wśród 52 cieniowych zaćmień Księżyca widocznych w
Polsce do roku 2040 będzie aż 33 typu całkowitego (chociaż nie
wszystkie będą widoczne w czasie maksimum ich fazy). Pośród
zaćmień półcieniowych zwracają uwagę 3 całkowite, z tym że to
trzecie (z roku 2017) staje się częściowym jeśli przyjąć francuski
sposób uwzględniania wpływu atmosfery Ziemi na rozmiary jej
półcienia (Meeus 1980).
Almanac for Computers, 1988, 12th edition, p. B14 (Eqs. 1 and 2),
Nautical Almanac Office, USNO, Washington (DC).
Astronomicheskij Ezhegodnik SSSR, 1990, Nauka, Leningrad (1988).
Borkowski K.M., 1987, Post. Astron. 35, 275.
Borkowski K.M., 1988, Astron. Astrophys. 205, L8.
Borkowski K.M., 1989, Solar Eclipses in Poland, 900 – 2200, Post.
Astronaut. 22, Nr 3/4, 99 – 130.
Borkowski K.M., 1990a, Lunar Eclipses in Europe, 900 – 2200,
Earth, Moon, and Planets 49, 107 – 140
Borkowski K.M., 1990b, Lunar Penumbral Eclipses, 1900 – 2200,
Earth, Moon, and Planets 49, 141 – 148
Bretagnon P., Simon J.L., Laskar J., 1986, J. Hist. Astron. 17, 39.
Chapront-Touze M., Chapront J., 1988, Astron. Astrophys. 190, 342.
Dagaev M.M., 1978, Solnechnye i lunnye zatmeniya, Nauka, Moskva.
Dagaev M.M., 1981, w: Astronomicheskij Kalendar' – postoyannaya
chast' (red. V.K. Abalakin), Nauka, Moskva, s. 149.
de Jong T., van Soldt W.H., 1989, Nature 338, 238.
Erman W., Tiomkin E., 1987, Mity starożytnych Indii, Pomorze,
Bydgoszcz.
Espenak F., 1987, Fifty Year Canon of Solar Eclipses: 1986 – 2035,
NASA RP-1178 Revised.
Explanatory Supplement AENA, 1961, Her Majesty's Stationery
Office, London, s. 257.
Fangor R., 1988, Urania (Kraków) LIX (9), 266.
Fangor R., 1990a, Zaćmienia Słońca i Księżyca, 1991 – 2000,
PTMA, Warszawa.
Fangor R., 1990b, Kanon polskich zaćmień Słońca i Księżyca, 2001
– 2200, PTMA, Warszawa.
Janiczek R., 1962, Kalendarz astronomiczny na XX w., PWN,
Warszawa.
Liu Bao-lin, 1983, Canon of Lunar Eclipses from 1000 BC to AD
3000, Publ. Purple Mountain Obs.(Nanjing), vol. 2, No. 1, 1 – 136.
Meeus J., 1980, J. R. Astron. Soc. Canada 74, 291.
Meeus J., Mucke H., 1983, Canon of Lunar Eclipses, - 2002 to
+2526, Astronomisches Buro, Vienna, Austria.
Merletti R.J., 1986, Sky Telescope 72 (5), 515.
Mucke H., Meeus J., 1983, Canon of Solar Eclipses, - 2003 to
+2526, Astronomisches Buro, Vienna, Austria.
Oppolzer T.R.v., 1887, Canon der Finsternisse, Vienna.
Pang K.D., 1987, J. Hydrol. 96, 139.
Pang K.D., Yau K., Chou H.-h., Wolff R., 1988, Vistas Astron. 31,
833.
Polozova N.G., 1955, Bull. Inst. Teor. Astron. 6, 202.
Raab H., 1988, Sky Telescope 75, 640.
Sharonov V.V., 1952, Astron. Circ. No. 130, 12.
Sofia S., Dunham D.W., Fiala A.D., 1980, w Proc. Conf. Ancient Sun
(red. R. O. Pepin i in.), s. 147.
Stephenson F.R., Clark D.H., 1978, Applications of Early
Astronomical Records, Adam Hilger Ltd, Bristol.
Stephenson F.R., Houlden M.A., 1986, Atlas of Historical eclipse
maps. East Asia 1500 BC – AD 1900, Cambridge University Press.
Stephenson F.R., Morrison L.V., 1984, Phil. Trans. R. Soc. London
A313, 47.
Stephenson F.R., Said S.S., 1989, Astron. Astrophys. 215, 181.
Wiland J., Zawilski M., 1986, Urania (Kraków) LVII, 331.
Zawilski M., 1990, Urania (Kraków) LXI, 2, 42, 75, 102,
137 i 177.
Tabela 1
Zaćmienia Słońca widoczne w Polsce w latach 1991 – 2040
obliczone dla geograficznego położenia Warszawy
Data Początek Maksimum fazy Koniec Rok M d CSE h V CSE h a V faza F Ds Dm CSE h V h m ° ° h m °
° ° % ' ' h m ° ° 1993 5 21 1618 27 299 1642 24 93 319 0,061 2 31,6 30,8 1705 20 339 1994 5 10 1838 4 194 1912 0 120 166 0,354 23 31,7 29,5 2014 -8 93 1996 10 12 1423 19 280 1535 10 64 343 0,658 56 32,1 30,7 1642 1 50 1999 8 11 1032 51 294 1151 53 4 195 0,858 83 31,6 32,5 1310 49 96 2003 5 31 327 0 291 424 7 243 17 0,837 77 31,6 29,7 524 16 102 2005 10 3 913 27 297 1021 32 341 232 0,421 30 32,0 30,4 1132 34 164 2006 3 29 1054 40 212 1157 41 6 138 0,537 44 32,0 33,6 1300 39 65 2008 8 1 952 49 4 1050 54 338 41 0,344 23 31,5 32,9 1148 56 75 2010 1 15 702 -6 220 743 0 306 188 0,019 0 32,5 29,5 749 1 183 2011 1 4 813 3 299 936 10 331 8 0,817 75 32,5 30,7 1104 15 74 2015 3 20 947 32 284 1056 37 345 345 0,723 66 32,1 33,8 1207 37 44 2021 6 10 1055 60 320 1154 61 9 340 0,196 10 31,5 30,0 1253 57 2 2022 10 25 1014 24 346 1123 26 1 35 0,521 41 32,2 32,0 1232 24 84 2025 3 29 1150 41 288 1228 40 16 312 0,157 7 32,0 33,7 1306 38 338 2026 8 12 1814 7 249 1902 0 115 192 0,850 82 31,6 32,6 1955 -7 92 2027 8 2 926 46 288 1022 52 328 226 0,413 30 31,5 33,9 1119 55 161 2029 6 12 326 1 358 353 4 236 30 0,122 5 31,5 30,4 420 7 60 2030 6 1 516 15 285 622 25 265 212 0,722 64 31,5 29,6 734 36 136 2034 3 20 1110 37 193 1149 38 2 155 0,147 7 32,1 33,4 1228 37 116 2036 8 21 1811 4 266 1843 0 110 289 0,570 48 31,6 33,4 1947 -9 58 2037 1 16 909 9 309 1036 15 343 6 0,638 53 32,5 29,9 1207 17 60 2038 1 5 1503 3 187 1534 0 52 160 0,215 11 32,5 31,2 1640 -9 93 2038 7 2 1511 41 154 1523 39 77 145 0,013 0 31,5 31,0 1534 37 136 2039 6 21 1826 11 239 1926 4 125 328 0,873 82 31,5 29,6 2022 -3 57
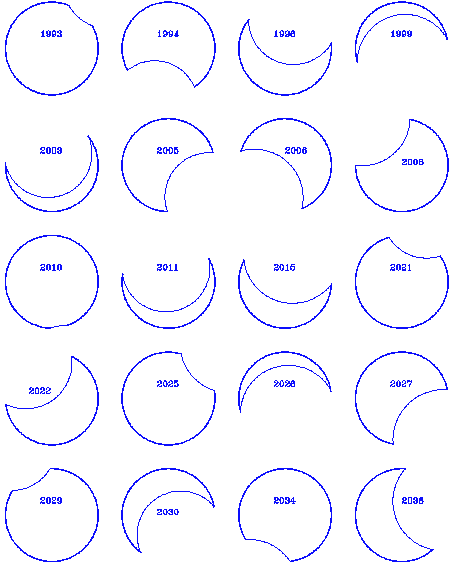
Ryc. 2.
Tabela 2
Zaćmienia Księżyca widoczne w Polsce w latach 1991 – 2040.
Wielkości h, a, V oraz W/Z dotyczą Warszawy
Data Początek Maksimum fazy Koniec W/Z Rok M d CSE h CSE h a V faza Dp Du Dm CSE h CSE h m ° h m ° ° ° '
' '
h m ° h m
1992 12 9 2259 60 2444 57 34 159 1,274 152,4 86,0 31,8 2629 45 3154
1993 11 29 540 13 726 -1 126 324 1,091 146,1 79,8 30,1 912 -12 719
1994 5 25 337 0 430 -8 66 149 0,248 156,7 92,1 33,2 523 -15 333
1996 4 3 2321 31 2510 28 26 2 1,383 149,3 84,0 31,1 2658 17 2908
1996 9 27 212 28 354 15 73 127 1,244 154,7 89,5 32,6 536 0 538
1997 3 24 357 14 539 -1 89 160 0,923 144,1 78,5 29,7 721 -16 534
1997 9 16 1808 3 1947 17 300 15 1,197 157,9 92,9 33,5 2125 28 1748
2000 1 21 402 30 543 15 102 327 1,330 157,3 90,9 33,1 725 1 735
2001 1 9 1942 35 2120 49 304 216 1,194 158,5 92,0 33,4 2259 58 1525
2003 5 16 303 5 440 -8 68 163 1,132 157,5 92,8 33,4 617 -22 343
2003 11 9 032 50 218 39 61 303 1,021 143,4 77,4 29,5 404 24 658
2004 5 4 1948 6 2130 15 330 42 1,308 156,3 91,5 33,1 2312 20 1858
2004 10 28 214 36 404 21 83 116 1,311 147,2 81,4 30,5 554 5 634
2006 9 7 1905 7 1951 13 302 3 0,188 157,7 92,8 33,4 2037 19 1815
2007 3 3 2230 42 2421 44 11 201 1,236 144,3 78,4 29,7 2611 35 3023
2008 2 21 243 35 426 20 80 349 1,109 149,7 83,6 31,1 609 5 641
2008 8 16 2035 13 2210 21 336 169 0,812 147,3 82,8 30,7 2344 24 1851
2009 12 31 1952 38 2022 43 288 230 0,080 157,7 91,2 33,2 2053 47 1509
2010 12 21 732 1 917 -9 149 165 1,260 152,1 85,7 31,7 1101 -15 743
2011 6 15 1923 -4 2112 7 327 199 1,704 151,7 87,4 31,9 2302 13 1954
2011 12 10 1345 -10 1532 1 234 33 1,110 145,9 79,5 30,1 1718 15 1524
2013 4 25 2052 14 2107 15 323 36 0,019 155,0 90,1 32,7 2123 17 1848
2015 9 28 207 28 347 15 71 307 1,282 158,0 92,8 33,5 527 1 536
2017 8 7 1822 -7 1920 2 299 202 0,250 145,6 81,2 30,3 2018 9 1908
2018 1 31 1248 -20 1430 -14 219 34 1,321 157,4 91,1 33,2 1611 -2 1628
2018 7 27 1924 -1 2121 12 326 193 1,612 142,4 78,1 29,4 2319 18 1929
2019 1 21 433 26 612 11 107 148 1,200 158,4 91,9 33,4 751 -2 739
2019 7 16 2101 7 2230 13 343 7 0,658 144,4 80,1 30,0 2360 15 1947
2022 5 16 327 1 511 -13 74 341 1,419 155,9 91,3 33,0 655 -28 337
2023 10 28 2034 39 2114 44 315 181 0,127 154,0 88,2 32,3 2153 48 1604
2024 9 18 312 17 344 13 67 297 0,088 157,7 92,7 33,4 416 9 520
2025 3 14 609 -2 758 -18 119 177 1,182 144,4 78,6 29,8 948 -31 555
2025 9 7 1726 -7 1911 9 293 6 1,366 153,5 88,7 32,3 2056 22 1810
2026 8 28 333 9 512 -5 80 115 0,934 147,0 82,3 30,6 652 -19 442
2028 1 12 444 26 513 22 98 154 0,070 157,5 91,0 33,2 541 17 753
2028 7 6 1808 -15 1919 -5 303 22 0,394 145,8 81,5 30,3 2030 3 2003
2028 12 31 1607 5 1751 19 257 231 1,250 151,8 85,3 31,6 1936 34 1523
2029 6 26 232 4 422 -8 61 140 1,848 152,1 87,8 32,0 612 -23 314
2029 12 20 2155 55 2341 60 4 3 1,121 145,7 79,2 30,0 2528 53 3156
2030 6 15 1820 -12 1933 -3 306 209 0,507 156,9 92,6 33,3 2045 5 1953
2032 10 18 1824 17 2002 31 298 198 1,106 155,5 89,9 32,8 2140 43 1626
2033 4 14 1824 0 2012 14 308 225 1,098 143,6 78,4 29,6 2160 24 1825
2034 9 28 330 17 346 15 70 307 0,019 155,0 89,8 32,7 401 13 534
2035 8 19 131 20 210 17 39 143 0,107 145,4 80,8 30,2 249 13 437
2036 2 11 2130 42 2311 50 345 23 1,305 157,6 91,3 33,2 2453 49 1620
2036 8 7 155 15 351 2 58 136 1,457 142,5 78,0 29,4 547 -14 411
2037 1 31 1321 -18 1460 -10 225 218 1,211 158,2 91,8 33,4 1639 2 1623
2037 7 27 332 2 508 -11 71 314 0,814 144,7 80,3 30,0 645 -25 345
2039 6 6 1823 -11 1953 1 310 222 0,889 157,5 93,1 33,4 2123 9 1948
2039 11 30 1611 6 1755 20 262 26 0,946 143,7 77,4 29,5 1938 36 1526
2040 11 18 1812 23 2003 39 291 199 1,401 148,0 81,9 30,7 2153 53 1532
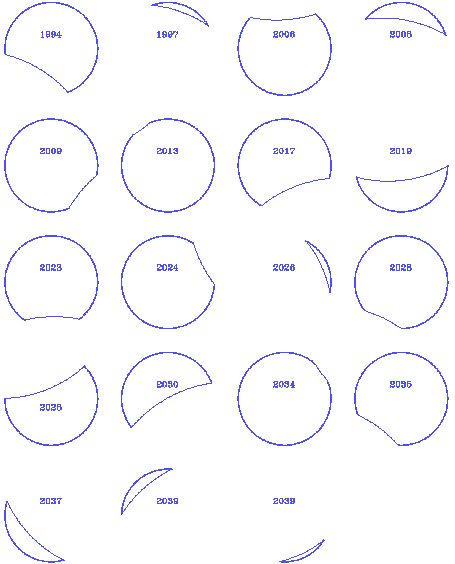
Ryc. 3.
Podobnie obliczylibyśmy czas upływający między wewnętrznymi
kontaktami z półcieniem biorąc w powyższym wzorze Dp
– Dm zamiast Dp +
Dm. Dodając do, i odejmując od, chwili środka zaćmienia
połowę obliczonego upływu czasu otrzymujemy pożądane momenty
kontaktów z półcieniem.
t arccos{cos[(Dp + Dm)/2]/cosσo}/arccos{cos[(Du + Dm)/2]/cosσo}.
Tabela 3
Półcieniowe zaćmienia Księżyca widoczne w Polsce w latach
1991 – 2040. Ostatnie cztery kolumny dotyczą Warszawy
Data Dane odnoszące się
do środka zaćmienia W/Z Rok M D CSE faza F/T t Dp Dm h a V CSE h m %/m m ' ' ° ° ° h m 1991 1 30 658.6 0.907 95% 241.6 155.9 32.8 2 114 345 714 1991 6 27 414.7 0.339 28% 177.1 142.4 29.4 -8 59 317 307 1991 7 26 1907.8 0.281 22% 161.1 143.0 29.6 -3 298 196 1926 1994 11 18 743.9 0.908 95% 276.5 143.3 29.4 -6 129 322 656 1995 10 8 1704.1 0.852 90% 252.2 148.4 30.9 2 262 201 1650 1998 3 13 520.0 0.735 77% 251.7 143.4 29.5 7 87 160 605 1998 8 8 324.8 0.147 8% 106.5 152.3 32.1 7 54 138 418 1999 1 31 1717.4 1.029 40m 265.9 151.4 31.6 7 254 48 1621 2002 6 24 2227.0 0.236 17% 137.2 149.8 31.4 11 344 15 2004 2002 11 20 246.5 0.887 93% 269.2 144.7 29.8 38 69 304 714 2006 3 14 2447.3 1.057 60m 292.1 143.4 29.5 39 20 197 3001 2009 2 9 1538.0 0.926 96% 243.0 156.1 32.8 -9 236 55 1645 2009 8 6 138.9 0.429 39% 196.6 142.9 29.5 17 30 139 419 2012 11 28 1532.8 0.943 97% 280.8 143.3 29.4 0 236 29 1534 2013 10 18 2450.0 0.791 84% 243.8 148.9 31.0 44 32 145 3029 2016 9 16 1954.0 0.934 97% 243.3 155.2 32.8 17 301 14 1751 2017 2 10 2543.6 1.015 28m 263.4 151.7 31.7 44 41 349 3101 2020 1 10 2009.7 0.922 96% 248.8 153.7 32.2 39 285 223 1524 2020 6 5 2024.7 0.594 60% 203.2 153.5 32.4 5 316 219 1941 2023 5 5 1822.5 0.990 100% 261.8 150.2 31.4 -7 291 60 1913 2024 3 25 812.4 0.983 100% 283.9 143.2 29.5 -24 120 177 533 2027 2 20 2412.4 0.953 98% 245.0 156.3 32.9 47 9 21 3038 2030 12 9 2327.1 0.969 99% 284.1 143.4 29.4 59 359 1 1512 2031 5 7 450.3 0.907 95% 241.5 154.6 32.6 -9 71 334 347 2031 10 30 845.0 0.743 78% 236.6 149.3 31.1 -16 142 143 627 2034 4 3 2005.2 0.881 93% 270.4 143.5 29.6 17 303 228 1803 2038 1 21 448.0 0.926 96% 250.0 153.4 32.1 25 92 146 746 2038 6 17 343.1 0.468 44% 181.9 153.8 32.5 -2 54 155 325 2038 12 11 1843.1 0.832 88% 263.5 144.5 29.7 28 270 31 1524
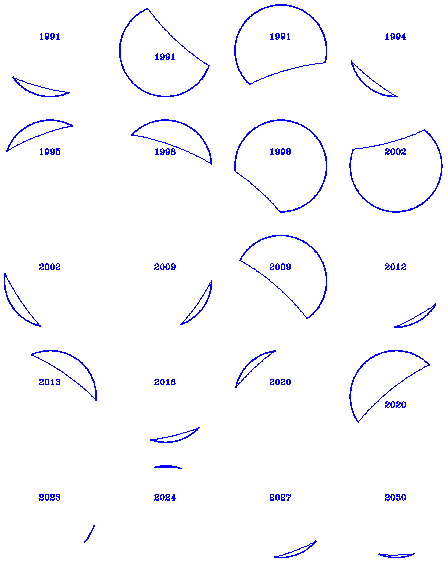
Ryc. 4.
LITERATURA
File translated from
TEX
by
TTH,
version 3.12 on 30 Jul 2002.