VLBI Correlator Can Perform Better

1. Introduction

Very long baseline interferometry (VLBI) is a powerful technique for studying radio source structures, source positions and baseline orientations with accuracies as high as a fraction of milliarcsecond, and in special cases approaching the microarcsecond level. When used as a geodetic instrument a VLB interferometer allows for measurements of baseline lengths of hundreds and thousands of kilometers with uncertainties as small as a few centimeters, what makes it unrivaled by other techniques.

High accuracy measurements are of crucial importance for many problems in different branches of science and technology. Therefore, the range of VLBI applications encompasses such diverse problems as fundamental questions concerning the overall evolution of the universe, the detailed properties and evolution of individual building blocks of the universe (central power houses of quasars and galaxies, cosmic masers, stars etc.), tests of general relativity, terrestrial and celestial reference frames, Earth rotation (time measurements), plate tectonics (drift of the continents), earthquake prediction and space navigation, to name but some.

The success of employing VLBI in each of the addressed field depends to a high degree on ever higher sensitivity and resolution of the technique. The potential accuracies lie still considerably ahead of these achieved so far. Factors that place actual limits on accuracy of VLBI measurements are numerous and generally well documented in literature. Yet, there are also some hidden sources of errors which, apparently, escaped attention of the researchers involved in highly sofisticated and time-consuming analyses of the collected observational material. I am referring here in general to not seldom, less or more open, statements in literature that a given analysis uncovers presence of errors of unknown origin and, to a greater extent, to the particular work of Wilkinson (1983; supplemented by personal communication of 1985). The real basis for this paper comes, however, from my earlier work (Borkowski 1986a, hereafter Paper I). I have demonstrated there that a digital correlator output is generally a strongly nonlinear function of the amplitude (or correlation coefficient) and phase of an input signal. While the output dependence on the amplitude appears basically the result of the infinite clipping of a video signal during recording, the dependence on phase is less fundamental and can be eliminated by improving the correlator alone. Both, when neglected, as in present day practice, necessarily lead to baseline-related errors. One may argue that these unpleasant errors are very small, but let the reader be not mislead by the magnitude since the same correlator is being used for reduction of less demending observations and these of high precision.

Throughout this writing I endeavour to show that relatively small and inexpensive complication of the VLBI correlator would directly repay in quality of its output. The essence of modification required is to make the so called fringe rotation function (hereafter FRF) a better approximation to a sinusoid than is actually practiced, for the sinusoidal FRF does not introduce phase dependent errors nor any additional losses of signal. For the convenience of a newcomer I remind that the aim of the fringe rotation during VLBI correlation process, which itself is an equivalent of a radio frequency conversion in mixers, is to lessen the fringe rate (or frequency), which originally is by far too high for convenient averaging of the correlation product, and is performed with the aid of a three-level approximation to a sinusoid (the levels are –1, 0 and 1). A modified correlator with a 5-level FRF (effective levels being –2, –1, 0, + 1 and + 2) would in turn greatly reduce errors caused by the dependence of the measured observables on the true fringe phase adding to it considerably smaller losses of the signal-to-noise ratio (SNR from now on).

In Sec. 3 I present one of possible ideas relevant to implementation of a multilevel fringe rotator and proceed to demonstrate superiority of such a correlator over the common 3-level one. This idea relies on the fact that VLBI correlators may in practice be faster than the speed they are actually run to cope with slow video recorders. Although most of the available improvement is gained with the 5-level FRF, I discuss first a general multilevel case and do not limit myself by the suggested approach to the implementation.

This final introductory paragraph I have prepared for the sceptic reader who may wonder why do I bother myself with so detailed analyses of the VLBI data processing while there exists such an abundance of literature on the subject. I have the following answer for him. The literature contains in fact much theoretical material related to signal processing. Nevertheless, it should be born in mind that, unfortunately, it is far from consistence and here and there offers different results. My approach being original is also quite simple, thus may serve well for all those who want to know how and why. As regards the 5-level FRF, pros and contras of its implementation have surely been discussed in internal reports in the course of years but, to the best of my knowledge, have never reached the literature. Noteworthy, the only such report I am aware of (1978 report of National Radio Astronomy Observatory by B. Rayhrer, M.J. Reid and D.B. Shaffer) contains serious flaws in part concerning the 5-level FRF. Such a statement is in obvious need of substantiation. The evidence lies in the results and method employed by the authors. Firstly, they have cut the harmonic content of their FRF to the first 14 nonzero harmonics with the effect of an underestimation (by 17%) of the harmonic power. Secondly, they use wrong formulae for the SNR to arrive at 3.8% instead of 2.2% for the loss in SNR. Moreover, their FRF differs significantly from the optimal 5-level FRF which, as will be shown later, guarantees the SNR losses to remain at the level as low as 1.3%. Should all the harmonics be accounted for, their formulae give 4.5% loss in SNR which unfavourably compares with the generally accepted 4% loss of the much rougher 3-level FRF. The following section is provided chiefly to clarify the concept of SNR losses in relation to digital VLBI correlators.

2. SNR loss

It is desired that signal processing be done so as to retain as much as possible of the SNR inherent in the data. When the SNR is high, however, the point is not critical. This alone justifies the SNR optimization considerations to be limited only to the case of small signals. Given a small input signal the expected fringes can be approximated by pure sine waves. The FRF or the weighting function w(φ), where φ stands for the (predicted) phase of the fringes, can be chosen to possess the cosine function symmetry. Fig. 1. illustrates such a function, wherein the 5-level FRF is plotted.

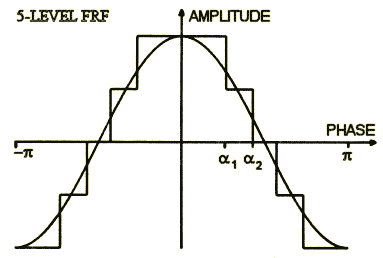Fig. 1.  An approximation of the cosinusoid by a 5-level fringe rotation function. The phase angles α1 and α2 were here chosen to be optimal with respect to the signal-to-noise ratio. Setting α1 = α2 = 3π/8 reduces this function to the 3-level FRF commonly used in practice

Qualitatively speaking, the maximum possible SNR will be achieved when w matches most closely the cosine function. More specifically, it can be shown that the loss factor for SNR due to imperfect shape of w is equal to the ratio of the amplitude of the first Fourier component of the w to the square root of the power (meaning the sum of squared amplitudes) contained in all the w's Fourier components. The harmonic amplitudes of our function w are represented by the following Fourier coefficients:

Ak =   0, for k = 2, 4, 6, ... n, 4 πk   n Σ j=1 (wj – wj+1)sin(kαj), for k = 1, 3, 5, ...,

(1)

where w_n+1 = 0. Thus the SNR loss factor is

L =   2 √ π n Σ j=1 (wj – wj+1)sin(αj) [ n Σ j=1 (wj2 – wj+12)αj ] 1/2   .

(2)

Though we spoke in terms of the harmonics of the weighting function the formula (2) can be derived in different ways not involving harmonic analysis, but here we will not ponder on this point any further (for that matter the interested reader may wish to consult Borkowski (1986b), where the assertion of validity of this approach is aimed upon).

Since we deal with digital correlators it is natural to choose the weights in such a manner that within each quarter of the FRF cycle the neighbouring values differ by one, i.e. |w_j – w_j+1| = 1. Then the nonzero (odd-numbered) amplitudes of (1) become simpler:

Ak = 4 πk Σ j sin(kαj),      k = 1, 3, 5, ...

and also Eq. (2) simplifies to

L = 2 Σsinαj [πΣ(2n – 2j + 1)αj]1/2 .

(3)

Proper choice of each α_j, which defines the range of phase to which the j-th weight is assigned to the synthesized FRF, is done by maximizing the loss factor. This, of course, minimizes losses in SNR.

The assumption of small signal is essential to the above discussion. When it is loosened the loss in SNR becomes fringe amplitude and phase dependent. Even now, however, the presented formulae for the L indicate certain values, that for numerically examined cases (a few tens in number) always were enveloped by the range of true ones. Whether this property holds in general or not remains to be demonstrated.

To have a useful check on validity of formula (3) and an example take n = 1 and w₁ = 1. Then Eqs. (2) and (3) reduce to

L = 2   sin α1 √ πα1 ,

which with the two-level FRF (α₁ = π/2) yields 0.9, and with the three-level FRF (α₁ = 3π/8) — 0.96. These numerical results are well known from literature (e.g. Moran 1976, Rogers 1980, Kawaguchi 1983), although they differ considerably from those given by Fridman (1982; also Gubanov et al. 1983). A critical account of the Fridman's results will be presented elsewhere (Borkowski 1986b).

3. Synthesizing multilevel FRF

To introduce the proposed idea of multilevel fringe rotation let us assume that an existing VLBI correlator (excluding its playback system for reasons of it being slow) can be made to run at the speed of n times the normal operational mode, with additional allowence of fetching n times one and the same pair of input data bits to be correlated. The two original data streams would thus be multiplied in number of bits, though no new information would be introduced since the inserted bits would be just copies of each bit read-in. The increased amount of data would be compensated by increased speed of the correlation process. Running so modified correlator module would give exactly the same output as prior to the modification. But now no further changes in the module hardware are necessary to realize the (2n + l)-level fringe rotation. To this end only the processor's program should be modified so as to generate n times slower FRF than before (to keep pace with the speed the original data bits are read) with the inhibition of correlation occurring many times on one period of FRF rather than twice as in the 3-level FRF. The inhibition or stoppage of the correlator effectively assigns the null weight to the correlation product by ignoring the data bits themselves. The means for this operation are actually built-in and normally used in contemporary correlators. Within the FRF period all n replicas of the fetched two bits which are to be assigned the highest weight, i.e. n or –n, are passed through correlator without inhibition. Of these with weights ±(n – m) only n – m are passed and for remaining m duplicates the correlator is inhibited. The usual accumulation and counting of passed correlated bits and their copies allows for calculation of the correlation coefficient.

Because the phase of fringes cannot be predicted with sufficient accuracy, to be able to detect fringes a correlator must incorporate two parallel channels in which FRFs are shifted in phase relative to each other by π/2. In one of the two quadrature channels the correlation amounts to

r^c =  Σxiyiw(φi) Σ|w(φi)| ,

(4)

where the weights w(φ_i) = FRF(φ_i)Σw^′_j, or the synthesized FRF, take on the values ±n, ±(n – 1), ..., 0 while the original FRF(φ_i) is the 2-level FRF and assumes values +1 and –1 (a digital correlator actually carries these operations on binary one bit values with 0 standing for –1, but this is inconsequential for our analysis). The w^′_j is here 1, if no correlator inhibition takes place and is zero otherwise. The x_i, y_i and φ_i in (4) are the two correlated bit streams and a model (a priori) fringe phase, respectively. Replacing the φ_i with π/2 – φ_i in Eq. (4) yields an expression for the correlation r^{^}_s in the other, sine, channel of the correlator. Note that this kind of the FRF synthesis in its simplest case (with n = 1) is actually performed by the usual 3-level correlator.

The described idea seems impractical for modification of the existing NRAO and Haystack correlators since it would require extensive changes (D. Graham's opinion in correspondence of 1984). Nonetheless, it does deserve due attention when the design of a new correlator is undertaken. Other schemes of the FRF synthesis which also do not involve multibit multiplication and do not rely on higher speed of the correlator module are of course possible and might be preferred from the technical point of view. This, however, will not be our concern here, and in fact the actual design is of minor importance and does not really affect the conclusions of this paper.

4. Response of correlator with multilevel rotator

The expected amplitude and phase of the fringes as measured at the correlator output can be derived in the way described in Paper I. For small signals, i.e. when the correlation coefficient r_o is close to zero, the sine channel output is

rs = E(r^s) = – 2 π q rosinφo,

(5)

where E(...) stands for the expectance operator, φ_o is the true phase of the fringes, and

L = n Σ j=1 (wj – wj+1)sin(αj) n Σ j=1 (wj – wj+1)αj .

(6)

It is due to the symmetry of the FRF that the summations in Eq. (6) could be limited to the indices pertaining only to the first quarter of the FRF.

In the quadrature channel r_c(φ_o) = r_s(π/2 – φ_o), so that the expected amplitude and phase are (here we assume additionally that the SNR after averaging of the two outputs is sufficiently high)

R = (r2s + r2c)1/2 = 2 π q ro,

(7)

Φ = atg rs rc  = φo,

(8)

respectively. The last two results are interpreted to mean that with the small signal approximation the measured phase is unbiased and the amplitude requires multiplication by a factor l/q, apart of the usual Van Vleck correction (π/2), to arrive at the correlation coefficient.

Assuming as before that successive weights drop in steps of 1 in the first quarter of FRF argument, we get this very simple form for the q factor:

q = Σ sinαj  Σ αj .

(9)

This analysis could be extended for the case of large signals. For general multilevel. FRF, however, the analytic description becomes tedious and situation complicates further for arbitrary r_o. Therefore, we will limit ourselves to presenting relevant results for the 5-level FRF only.

5.   5-level correlator response

Let us consider now the 5-level fringe rotator, which requires the doubling (n = 2) of the normal operational speed of the usual correlator if the earlier described synthesis is implemented. In this case from (4) we have:

L =   2 √ π  sinα1 + sinα2 (3α1 + α2)1/2   ,

(10)

which reaches a maximum of 0.9868 at α₁ = 0.8407 and α₂ = 1.3466 rad. Hence the loss in SNR, as compared to the sine wave FRF, is only about 1.3%, that is three times lower than with the 3-level FRF. The maximum of L is relatively flat, so that setting the alphas at values even considerably different from these optimal may still result in insignificant additional losses. The numerical results given in the remainder of this section refer to these angles rounded to 7π/30 = 0.733 and 13π/30 = 1.36, implying L = 0.985. They were chosen solely because of an initial misinterpretation of a promisingly interesting distribution of harmonics, but any set closer to the optimal values would do even better.

For small signals the output of a correlator with 5-level rotator is described by Eqs. (5), (7) and (8) with

q =  sinα1 + sinα2 α1 + α2 ,

(11)

thus the measured fringe amplitude is to be corrected by the factor of 1.2714π/2 = 2.00 while calculating the correlation coefficient. For very large signals, i.e. when r_o ≈ 1, the sine channel output can be shown to be

rs(φo) =  2roφo/(α1 + α2), –α1 ≤ φo ≤ α1, ro(α1+ φo)/(α1 + α2),  α1 ≤ φo ≤ α2, ro, α2 ≤ φo ≤ π/2,

(12)

with the sine function symmetries: r_s(–φ_o) = –r_s(φ_o) = r_s(φ_o ±π). Since here we have also r_c(φ_o) = r_s(π/2 – φ_o), the expected outputs of this correlator can be calculated straightforwardly. Without going into details it is clear that both, the phase Φ and the amplitude R will depend on the true phase φ_o.

In the case of intermediate values of r_o a computer modeling is needed to trace the correlator response. We refer to Paper I for description of such modeling. This shows that with the 5-level FRF the dependence of the fringe amplitude R on the fringe phase φ_o remains below 0.3% of R for r_o < 0.55, thus it may be quite safely neglected in most of the VLBI applications. The correlation coefficient can be calculated from the measured amplitudes with the approximation

ro ≈ sin[2R – (3 – R)R2/5],

(13)

which is accurate to better than 0.3% of r_o for r_o < 0.6, and for all phases. Assumption of small signals allows to reduce Eq. (13) to r_o ≈ 2R, which is consistent with already presented analytical derivation. The measured phases Φ are expected to differ systematically from the true phases φ_o by less than 0.5° for r_o < 0.99, and less than 0.1° for r_o < 0.5. To better appreciate these numbes recall that for the 3-level FRF and r_o < 0.5 the corresponding uncertainties of the amplitude and phase are 1% and 1°, respectively (Paper I), i.e. roughly one order of magnitude worse. Worth noticing is also the closeness of the response of the correlator with the 5-level FRF to that with the perfect sine wave FRF (Eq. (16) in Paper I).

6. Conclusion

Baseline-related errors limit the accuracy of high precision VLBI observations. The errors do not cancel in so called closure observables thus they affect the high dynamics maps as produced through the use of highly perfected image recovery procedures. Similar signature of these errors is expected of the phase referencing techniques used in precision astrometry since these techniques rely on exactitude of error cancelation in differenced observables.

This paper presents an attempt to investigate the feasibility of improving digital VLBI correlators in order to attain higher quality outputs. The attention was focused exclusively on a fringe rotator, which in present-day correlators is too crude to adequately simulate a perfect mixer. The outcome of the oversimplification of the fringe rotation are an extra loss of signal and, more importantly, biases of measured observables. The performance of a correlator with a 5-level rotator have been analysed in respect of signal-to-noise ratio (SNR) losses and quality of its response. This suggests that somewhat greater complexity of the 5-level rotator rewards in significantly better observable estimators.

One approach to implementation of the higher-than-three-level rotator has been detailed. It relies on potentially higher speed of the correlator as opposed to the speed of the video recorders used in the playback system. The latter limits the overall speed of the processing. The only modification required in the processor hardware is one that enables the correlator module a multiple fetching of the same pair of input bits in time normally allocated for one cycle of correlation of that bit pair. The modification now allows the processor to be run at any reasonable speed to yield exactly the same output as prior to the change, provided the accumulation time is not critical, synchronism is kept with the playback system, and the fringe rotation is adequately slowed down. Final modification concerns the software, which now should be able to inhibit the correlator in a defined manner to effectively produce a desired multilevel fringe rotation function.

It was shown that doubling the speed and introducing inhibition pattern corresponding to the 5-level rotator yields outputs that are very close to the case of the perfect fringe rotation for a wide range of the correlation coefficient. As compared to the commonly used 3-level rotation scheme this reduces the losses in SNR by the factor of three (from 4% to 1.3%). Still higher gains result in quality of signal parameter estimators. The maximum bias due to the phase dependence of the output amplitude is reduced by a factor of about 5, while the departures of expected phase from the true values are compressed about 10 times (both these factors refer to the case of relatively strong signal, r_o ≈ 0.5, but presumably are respresentatitve of weaker signals as well). Except for the SNR considerations the quoted gain factors become illusory when signals get very small since then the biases become very small themselves.

Acknowledgements. The study presented in this paper was in part financially supported through the Polish Government research problem RPB Nr RR.I. 11/2. The author thanks dr Z. Turło for pointing out erratic enunciations concerning the harmonic content of the FRF, present in the original version of this work and only touched upon in Sec. 5 here.

REFERENCES

Borkowski, K.M., 1986a, Astron. Astrophys., 157, 91 (Paper I).

Borkowski, K.M., 1986b, Astrophys. Space Sci., 128, 443.

Fridman, P.A., 1982, Astrofiz. Issled., Izv. Spets. Astrofiz. Observ., 17, 95.

Gubanov, V.S., Finkel'shtejn, A.M., and Fridman, P.A., 1983, Vvedenie v radioastrometriyu (Nauka, Moskva), p. 220.

Kawaguchi, N., 1983, J. Radio Res. Lab., 30, 59.

Moran, J.M., 1976, Meth. Exper. Phys., 12C, 174.

Rogers, A.E.E., 1980, in Radio Interferometry Techniques for Geodesy, NASA Conference Publ. 2115, p. 275.

Wilkinson, P.N., 1983, in Very Long Baseline Interferometry Techniques, CNES (Cepadues Editions, Toulouse) p. 375.