Teoretyczne charakterystyki
radioteleskopu RT32
| Theoretical patterns of the RT32 radio telescope.
SUMMARY: General formulae for voltage (cf. Eq. 5) and power
pattern of a parabolic antenna (whose diameter is D) with subreflector (with
the diameter of d) are derived. These are then applied to the Toruń 32 m
radio telescope design assuming
the illumination function of the form
1 - b(2r/D)2, where
b = 0.75 and r is the radial distance from
the paraboloid axis. Detailed structure of main beam and sidelobes
are presented graphically. Numerical values of parameters such as the half
power beamwidth at different frequencies, the telescope directivities and
surface efficiency (or aperture loss factor due to nonuniform illumination)
are given.
|
Wiele z parametrów charakteryzujących 32-metrowy radioteleskop
opisano w fazie projektowania
(zob. też uzupełnienie) tego instrumentu . Niniejszy artykuł jest
poświęcony analizie teoretycznej charakterystyki kierunkowej i parametrów
z nią związanych.
Dla dowolnego układu anten wypadkowa
charakterystyka kierunkowa i widmo częstości przestrzennych tego układu są
parą transformat Fouriera. Innymi słowy, aby wyznaczyć charakterystykę
kierunkową systemu antenowego należy obliczyć dwuwymiarową transformatę
Fouriera z rozkładu powierzchni zbierających tego systemu (ściślej:
rozkładu pola elektrycznego na aperturze).
Jeśli funkcja rozkładu f(x,y) jest kołowo symetryczna, to także jej
widmo ma taką symetrię. W tym przypadku do pary transformat możemy podstawić
współrzędne biegunowe: x = r cosf i
y = r sinf oraz,
w dziedzinie częstości przestrzennych,
u = q cosj i v = q sinj,
uzyskując zależność od jednej
tylko zmiennej (r lub q). Jakobiany tych przekształceń współrzędnych
wynoszą r oraz q. Dla pierwszej z pary transformat mamy kolejno:
Ą
ó
ő
-Ą |
Ą
ó
ő
-Ą
|
f(x,y) e–j2p(ux + vy) dxdy
= |
Ą
ó
ő
0 |
2p
ó
ő
0
|
f(r)e–j2prq(cosfcosj + sinfsinj)r drdf |
|
|
= |
Ą
ó
ő
0 |
f(r) | é
ë |
2p
ó
ő
0 |
e–j2prq
cos(f - j)
df |
ů
ű |
r dr = 2p |
Ą
ó
ő
0 |
f(r)Jo(2pqr)r dr = F(q), |
|
gdzie Jo(z)
= 1/(2p)ň02pexp(–jz cosF)
dF
= 1/pň0pcos(z cosF)
dF
jest funkcją Bessela. Funkcję F(q) nazywa się transformatą
Hankela (zerowego rzędu) funkcji f(r). Podobnie dla transformaty
odwrotnej dostajemy łatwo:
|
f(r) = 2p |
Ą
ó
ő
0 |
F(q)Jo(2pqr)q dq, |
|
co jest odwrotną transformatą Hankela (zauważmy, że obie mają taką samą
formę i jądro).
W szczególności zatem, transformata Fouriera jednostkowego dysku
(równomiernego rozkładu pola promieniowania na aperturze kołowej)
o średnicy D, czyli funkcji P(r/D), ma postać funkcji Bessela
pierwszego rzędu (R. Bracewell, The Fourier Transform and Its
Applications, 1965):
|
2p |
Ą
ó
ő
0
|
P( | r
D
|
) Jo(2pqr)r dr = |
D
2q
|
J1(pDq) = 2p |
ć
č
|
D
2
|
ö
ř
|
2
|
J1(pDq)
pDq
|
, |
| (1) |
a funkcji postaci [1 -
(2r/D)2]P(r/D) —
|
|
J2(pDq)
pq2
|
= |
pDq
4
|
|
J1(pDq) + J3(pDq)
pq2
|
= p |
ć
č
|
D
2
|
ö
ř
|
2
|
|
J1(pDq) + J3(pDq)
pDq
|
|
| (2) |
gdzie skorzystaliśmy z następującej własności funkcji Bessela:
|
|
2n
z
|
Jn(z) = Jn-1(z) + Jn+1(z). |
|
Równomiernie oświetlona apertura kołowa z kołowym otworem o średnicy d w środku,
P(r/D) – P(r/d), odpowiada
zatem charakterystyce:
|
2p |
ć
č
|
D
2
|
ö
ř
|
2
|
|
J1(pDq)
pDq
|
- 2p |
ć
č
|
d
2
|
ö
ř
|
2
|
|
J1(pdq)
pdq
|
= |
pD2
2
|
|
é
ë
|
J1(z)
z
|
- |
ć
č
|
d
D
|
ö
ř
|
2
|
|
J1(z d/D)
zd/D
|
ů
ű
|
. |
| (3) |
Przy nierównomiernym oświetleniu z (2) otrzymamy analogicznie:
|
|
J2(pDq)
pq2
|
- |
J2(pdq)
pq2
|
= p |
ć
č |
D
2
|
ö
ř |
2
|
J1(pDq)
+ J3(pDq)
pDq
|
-
p |
ć
č |
d
2
|
ö
ř |
2
|
J1(pdq)
+ J3(pdq)
pdq
|
. |
| (4) |
W praktyce rozkład pola na aperturze widziany przez urządzenia
odbiorcze nigdy nie jest równomierny, gdyż charkterystyka kierunkowa
oświetlaczy nie jest funkcją stałą. Często przyjmuje się, że oświetlenie
maleje z odległością od środka właśnie jak (r/D)2, do –12 dB na brzegu
dysku w stosunku do jego środka. Dla apertury z otworem taki rozkład pola
opisuje funkcja postaci:
|
(1 - b)[P( |
r
D
|
) - P( |
r
d
|
)] + b[1
– (2r/D)2][P( |
r
D
|
) - P( |
r
d
|
)], |
|
gdzie b = 0.75, co odpowiada wspomnianym 12 dB
[tj. 10lg(0.252)].
W powyższym wyrażeniu lewy składnik w przeciwdziedzinie (tj. po
transformacji) odpowiada przeskalowanej funkcji (3), zaś
składnik prawy — (4).
Charakterystyka kierunkowa takiego rozkładu pola ma więc postać:
p
4 |
D2 |
é
ë |
(1 - b) |
2J1(z)
z
|
+ b |
J1(z)
+ J3(z)
z |
ů
ű |
– |
p
4 |
d2 |
é
ë |
(1 - b) |
2J1(z d/D)
z d/D |
+ b |
J1(z d/D)
+ J3(z d/D)
z d/D |
ů
ű |
|
|
|
= |
p
4 |
D2 |
é
ë |
(2 - b) |
J1(z)
z |
+ b |
J3(z)
z |
ů
ű |
- |
p
4 |
d2 |
é
ë
|
(2 - b) |
J1(z d/D)
z d/D
|
+ b |
J3(z d/D)
z d/D
|
ů
ű
|
|
|
czyli jest proporcjonalna do:
|
(2 - b) |
J1(z)
z
|
+ b |
J3(z)
z
|
- |
d
D
|
|
é
ë |
(2 - b) |
J1(z d/D)
z
|
+ b |
J3(z d/D)
z |
ů
ű
|
|
|
albo
U(z) ~ |
|
J1(z) + |
b
2
– b |
J3(z)
– | d
D |
é
ë |
J1(z d/D) + |
b
2 –
b |
J3(z d/D) |
ů
ű |
z
|
. |
|
(5) |
Ten wynik jest w przybliżeniu równoważny wzorowi podanemu w opracowaniu
RT32 – Podręcznik obserwatora Centrum Astronomii UMK, 1996/2003):
|
U(z) ~ [2bJ2(z)/z + (1 - b)J1(z) - J1(zd/D) d/D]/z. |
|
Przybliżenie bierze się stąd, że we wzorze 'podręcznikowym' zaniedbano
niewielki przyczynek pochodzący od nierównomierności oświetlenia samego
otworu w aperturze.
Wykres znormalizowanych funkcji U oraz
U2
dla d/D = 0.1 i b = 0.75
(Plot of the normalized voltage and power pattern functions)
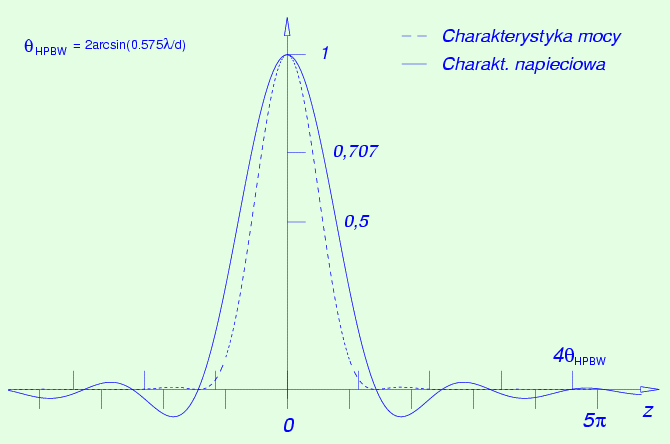
Prawa strona (5) przy z ® 0
zmierza do wartości [1 - (d/D)2]/2,
którą można użyć do znormalizowania charakterystyki. Oto przykład
fortranowskiego programu obliczającego znormalizowaną funkcję U(z):
function chaRT32(z)
c Program liczy napieciowa charakterystyke RT32 w funkcji argumentu
c z = pi*D/lambda*sin(theta). Odbierana moc wynosi chaRT32(z)**2.
c Znormalizowana napieciowa charakterystyka pełnego dysku (bez otworu)
c z oswietleniem slabnacym ku brzegowi czaszy jak 1 - beta*(2*r/D)**2:
dysk(z)=2*( bessj1(z) + beta/(2-beta)*bessj(3,z) )/z
c Uzyte powyzej funkcje Bessela sa dostepne w "Numerical Recipes"
c Charakterystyka dysku z otworem hole = d/D i 12-dB tlumieniem:
beta=0.75 ! taper 12 dB na brzegu czaszy
hole=0.1 ! otwor 0.1 srednicy czaszy
holeSq=hole*hole
chaRT32=( dysk(z) - holeSq*dysk(z*hole) )/(1 - holeSq)
end |
Z teorii anten wiadomo, że jeżeli w argumencie charakterystyki
z = pDq średnicę D wyrazimy w długościach fali,
l, to q jest kosinusem kierunkowym (kosinusem
kąta między kierunkiem na niebie a płaszczyzną apertury). Argument ten
możemy zatem wyrazić w funkcji kąta q liczonego
od kierunku maksimum wzmocnienia (prostopadłego do płaszczyzny apertury):
gdzie l jest długością fali obserwowanego
promieniowania. Dysponując funkcją typu charRT32 łatwo teraz
obliczać kierunkową charakterystykę mocy (kwadrat charakterystyki
napięciowej) w funkcji kąta q.
W Fortranie kod może mieć np. postać prostej statement function:
char2(theta)=chaRT32(pi*Dlambda*sin(theta))**2
|
gdzie theta = q, pi
= p oraz Dlambda =
D/l.
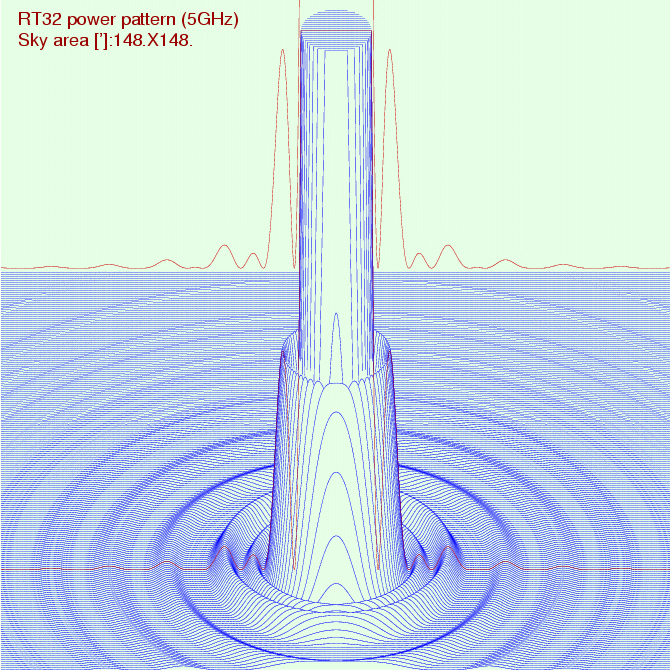
Poniższe trzy rysunki przedstawiają przestrzenny wygląd charakterystyki
radioteleskopu o aperturze kołowej o średnicy D = 32 m z centralnym otworem
(cień lustra Cassegraina) o średnicy 3.2 m we współrzędnych kątowych
obliczonych dla częstości
5 GHz (l = 6 cm) i przy oświetleniu z parametrem
b równym 0.75. Rysunki obejmują kwadratowe
pole o boku 148' w pobliżu maksimum wzmocnienia. Na rysunkach zaznaczano
(innym kolorem) również
pełne (niezacienione) przekroje przez maksimum charakterystyki. Charakterystyki
mocy promieniowania zostały przeskalowane w amplitudzie o czynniki ok. 100 i
ok. 4000 w stosunku do charakterystyki napięciowej, by pokazać strukturę
bardzo słabych listków bocznych.
Teoretyczna charakterystyka napięciowa
RT32 (Voltage pattern)

Teoretyczna kierunkowa charakterystyka
promieniowania RT32 (Power pattern)
Najwyższy pierścień wokół obciętej wiązki głównej, czyli pierwszy
listek boczny,
jest ok. 150 razy niższy od maksimum tej wiązki.
Ta sama charakterystyka mocy
przeskalowana o czynnik 40 (Same pattern rescaled for details)

Numerycznie wyznaczone położenia i poziomy ekstremów charakterystyki
kierunkowej RT32.
W pierwszej kolumnie tabeli (Nr) widnieją numery
kolejnych listków bocznych; 'min' oznacza minimum między listkami;
wiersz oznaczony '0.5' zawiera dane o poziomie połowy mocy głównej wiązki;
kąty q odpowiadające argumentowi z podano
w minutach łuku w siedmiu ostatnich kolumnach, każda dla innej częstości
wymienionej w główce tabeli.
Nr z/p Moc Kąty q ['] na poszczególnych częstościach [GHz]
*106 1.42 1.66 5 11.7 22 30 100
0.5 0.575204 500000 13.0 11.2 3.7 1.58 0.84 0.62 0.19
min 1.43414 0 32.5 27.8 9.2 3.95 2.10 1.54 0.46
1 1.83802 6694.4 41.7 35.7 11.8 5.06 2.69 1.97 0.59
min 2.49654 0 56.6 48.4 16.1 6.87 3.65 2.68 0.80
2 2.84525 460.1 64.5 55.2 18.3 7.83 4.17 3.05 0.92
min 3.27229 0 74.2 63.5 21.1 9.01 4.79 3.51 1.05
3 3.83027 709.6 86.9 74.3 24.7 10.54 5.61 4.11 1.23
min 4.57278 0 103.7 88.7 29.5 12.59 6.69 4.91 1.47
4 4.82960 17.0 109.6 93.7 31.1 13.29 7.07 5.18 1.56
min 5.10604 0 115.8 99.1 32.9 14.06 7.47 5.48 1.64
5 5.80383 255.9 131.7 112.6 37.4 15.98 8.50 6.23 1.87
min 6.67868 0 151.5 129.6 43.0 18.38 9.78 7.17 2.15
6 6.82003 0.5 154.7 132.4 43.9 18.77 9.98 7.32 2.20
min 6.96580 0 158.0 135.2 44.9 19.17 10.20 7.48 2.24
7 7.78250 116.0 176.6 151.0 50.1 21.42 11.39 8.35 2.51
min 8.69320 0 197.3 168.7 56.0 23.93 12.73 9.33 2.80
8 8.81618 0.1 200.1 171.1 56.8 24.27 12.91 9.46 2.84
min 8.94209 0 202.9 173.6 57.6 24.62 13.09 9.60 2.88
9 9.76714 51.9 221.7 189.6 62.9 26.89 14.30 10.49 3.15
min 10.5756 0 240.1 205.3 68.1 29.11 15.48 11.35 3.41
10 10.8130 0.9 245.5 209.9 69.7 29.77 15.83 11.61 3.48
min 11.0613 0 251.1 214.7 71.3 30.45 16.19 11.87 3.56
11 11.7585 20.7 267.0 228.3 75.7 32.37 17.21 12.62 3.79
min 12.4378 0 282.4 241.5 80.1 34.24 18.21 13.35 4.01
|
Jednym z ważniejszych parametrów charakterystyki promieniowania
radioteleskopu jest szerokość połówkowa głównej wiązki
qHPBW,
tj. podwojona wartość kąta q, przy którym
funkcja U maleje do
Ö{0.5} »
0.707 wartości w maksimum. Przekształcając (6) otrzymujemy:
|
qHPBW = 2 arcsin |
ć
č
|
zHPBW
p |
l
D
| ö
ř |
. |
|
W przypadku RT32 z obliczeń numerycznych wynika, że
zHPBW = 0.575204 p.
To wyznaczenie pozwala obliczać spodziewane rozdzielczości kątowe RT32 dla
różnych częstości. W poniższej tabelce zebrano przykładowe wyliczenia
Q =
qHPBW
dla kilku praktycznie użytecznych częstości
(f = c/l, gdzie c – prędkość światła).
f [MHz] 327 408 610 1420 1660 2290 5000 11700 22000 30000 1E5
l [cm] 91.68 73.48 49.15 21.11 18.06 13.09 5.996 2.562 1.363 0.999 0.300
Q ['] 113.3 90.81 60.74 26.09 22.32 16.18 7.410 3.167 1.684 1.235 0.371
Q [°] 1.89 1.51 1.01 0.435 0.372 0.270 0.124 0.053 0.028 0.021 0.006
D/1000 11 17 37 202 276 526 2510 13700 48500 90200 1E6 |
Parametr w ostatnim wierszu tej tabelki jest kierunkowością teleskopu
zdefiniowaną jako
D = 4p/W
= 4pU2(0)/[2pňU2(q)sinq dq],
gdzie całkowanie zostało przeprowadzone w zakresie
0 < q < p/2.
Otrzymany z tego całkowania kąt bryłowy jest też miarą powierzchni
skutecznej teleskopu, Aeff
= l2/W:
Aeff = 716.723 m2.
Liczba ta naturalnie odzwierciedla jedynie straty powierzchni wynikające
z przesłaniania subreflektorem i z nierównomiernego oświetlenia apertury.
Samo nierównomierne oświetlenie w założonej postaci wnosi straty:
804.25 – (716.723 + 8.0425) = 79.4845 m2, tj. 100*79.4845/804.25 =
9.88 % apertury.
— KMB
File translated from
TEX
by
TTH,
version 3.33 on 19 Mar 2003 (modified 2003.04.05).




