Jest też dostępna
druga część tego
raportu
(znacznie ciekawsza i z kolorowymi obrazkami!).
Teoretyczne charakterystyki
radioteleskopu RT32
| Theoretical patterns of the RT32 radio telescope.
SUMMARY: General formulae for voltage (cf. Eq. 5) and power
pattern of a parabolic antenna (whose diameter is D) with subreflector (with
the diameter d) are derived. These are then applied to the Toruń 32 m
radio telescope design assuming
the illumination function of the form
1 – β(2r/D)2, where
β = 0.75 and r is the radial distance from
the paraboloid axis. Detailed structure of main beam and sidelobes
are presented graphically. Numerical values of parameters such as the half
power beamwidth at different frequencies, the telescope directivities and
surface efficiency (or aperture loss factor due to nonuniform illumination)
are given. See also a sequel to this report (still
more interesting and witth color pictures!).
|
Wiele z parametrów charakteryzujących 32-metrowy radioteleskop
opisano w fazie projektowania
(zob. też uzupełnienie) tego instrumentu . Niniejszy artykuł jest
poświęcony analizie teoretycznej charakterystyki kierunkowej i parametrów
z nią związanych.
Dla dowolnego układu anten wypadkowe widmo częstości przestrzennych (które bezpośrednio wiąże się z charakterystyką kierunkową) i apertura tego układu
są parą transformat Fouriera. Innymi słowy, aby wyznaczyć charakterystykę
kierunkową systemu antenowego należy obliczyć dwuwymiarową transformatę
Fouriera z rozkładu powierzchni zbierających tego systemu (ściślej:
z rozkładu pola elektrycznego na aperturze).
Jeśli funkcja rozkładu f(x,y) jest kołowo symetryczna, to także jej
widmo ma taką symetrię. W tym przypadku do pary transformat możemy podstawić
współrzędne biegunowe: x = r cosφ i y = r sinφ oraz,
w dziedzinie częstości przestrzennych, u = q cosψ i v = q sinψ,
uzyskując zależność od jednej tylko zmiennej (r lub q). Jakobiany tych
przekształceń współrzędnych wynoszą r oraz q. Dla pierwszej z pary
transformat mamy kolejno:
∞
∫
–∞
∞
∫
–∞
f(x,y) e–j2π(ux + vy) dxdy
= |
∞
∫
0 |
2π
∫
0
|
f(r)e–j2πrq(cosφcosψ + sinφsinψ)r drdφ | | |
|
|
= |
∞
∫
0 |
f(r) | [ |
2π
∫
0 |
e–j2πrq
cos(φ – ψ)
dφ |
] |
r dr = 2π |
∞
∫
0 |
f(r)Jo(2πqr)r dr = F(q), |
|
gdzie Jo(z)
= 1/(2π)∫02πexp(–jz cosΦ)
dΦ
= 1/π∫0πcos(z cosΦ) dΦ
jest funkcją Bessela. Funkcję F(q) nazywa się transformatą
Hankela (zerowego rzędu) funkcji f(r). Podobnie dla transformaty
odwrotnej dostajemy łatwo:
|
f(r) = 2π |
∞
∫
0 |
F(q)Jo(2πqr)q dq, |
|
co jest odwrotną transformatą Hankela (zauważmy, że obie mają taką samą
formę i jądro).
W szczególności zatem, transformata Fouriera jednostkowego dysku
(równomiernego rozkładu pola promieniowania na aperturze kołowej)
o średnicy D, czyli funkcji Π(r/D), ma postać funkcji Bessela
pierwszego rzędu (R. Bracewell, The Fourier Transform and Its
Applications, 1965):
|
2π |
∞
∫
0
|
Π(r/D) |
Jo(2πqr)r dr = |
D
2q
|
J1(πDq) = 2π (D/2)2 |
J1(πDq)
πDq
|
, |
| (1) |
zaś obciętej funkcji parabolicznej, [1 – (2r/D)2]Π(r/D),
|
|
J2(πDq)
πq2
|
= 4π(D/2)2 |
|
J2(πDq)
(πDq)2
|
| . |
| (2) |
W praktyce rozkład pola na aperturze widziany przez urządzenia
odbiorcze nigdy nie jest równomierny, gdyż charkterystyka kierunkowa
oświetlaczy nie jest funkcją stałą. Często przyjmuje się, że oświetlenie
maleje z odległością od środka właśnie jak (2r/D)2, lecz nie do zera
na brzegu dysku tylko o pewien ułamek, β, wartości w jego środku. Taki rozkład można wyrazić w postaci sumy rozkładu równomiernego (o amplitudzie
1 – β) i parabolicznego (o amplitudzie β):
1 – β(2r/D)2
= [1 – β] + β[1 – (2r/D)2]
A zatem jego transformata Hankela będzie odpowiednio ważoną sumą transformat
powyższych dwóch składników pomonożonych przez funkcję prostokątną, Π(r/D):
|
(1 – β)2π(D/a)2 |
J1(πDq)
πDq
|
+ β4π(D/a)2
J2(πDq)
(πDq)2
|
= |
πD2
2z
|
| [(1 – β)
J1(z)
|
+ | 2β
|
J2(z)
z
| ]. | |
| (3) |
Po znormalizowaniu wyrażenia (3) do jedności w maksimum dostajemy następującą postać charakterystyki kierunkowej prostego paraboloidu:
|
|
Uo(β,z) |
= |
4
(2 – β)z
|
[(1 – β)
J1(z)
|
+ | 2β
|
J2(z)
z
| ] |
. |
| (4) |
Dla podobnie oświetlonej apertury z otworem w środku, tak jak
w przypadku teleskopu typu Cassegraina, charakterystyka kierunkowa jest
różnicą charakterystyk wyżej rozpatrywanego pełnego dysku i podobnego
dysku odpowiadającego wspomnianemu otworowi (cieniowi subreflektora).
Jeśli otwór ma średnicę κ razy mniejszą od D (d = κD),
osłabienie oświetlenia na jego brzegu wyniesie βs = βκ2, a ułamek całkowitego
napięcia pola apertury przypadający na otwór —
u = κ2 (2 – κ2β)/(2 – β).
Znormalizowana charakterystyka napięciowa teleskopu Cassegraina będzie więc
miała postać:
|
U(κ,β,z) = |
Uo(β,z) –
u Uo(κ2β,κ z)
1 – u
|
. |
|
| (5) |
Wydaje się, że jest to oryginalny wynik, gdyż nie ma go w dostępnej literaturze.
Poprawność tego analitycznego sformułowania została sprawdzona przez porównanie
z obliczeniami numerycznymi z wykorzystaniem bezpośredniej transformacji Fouriera
(przykładowe wyniki podano w tym raporcie). Właśnie
takie porównania wykazały, że na pozór oczywiste rozwiązanie przedstawione w
pierwotnej wersji tego dokumentu jest niedobre.
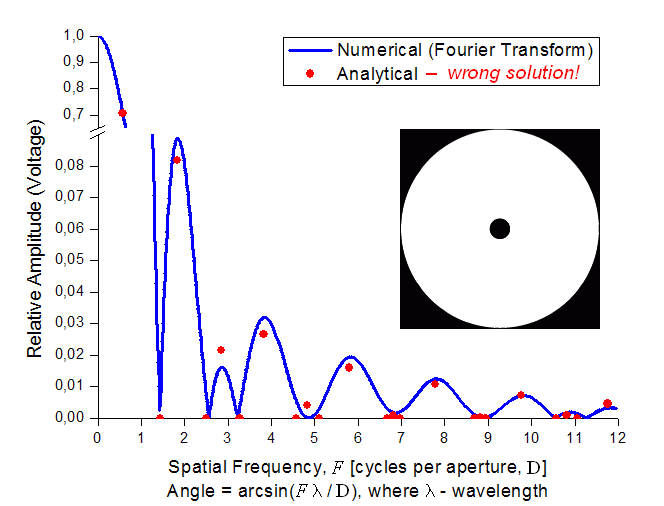
Różnice między poprawnym rozwiązaniem i tym niedobrym pokazuje poniższy rysunek.
| Widmo przestrzenne apertury teleskopu Cassegraina
ze stosunkiem średnic zwierciadeł d/D = κ = 0.1 i oświetleniem parabolicznym
z β = 0.75 (krzywa niebieska) oraz położenie ekstremów wzięte z tabeli opartej na błędnym rozwiązaniu (czerwone punkty).
|
Poniższa ramka zawiera przykład fortranowskiego programu do obliczania
znormalizowanej charakterystyki napięciowej RT32, który został wykorzystany
do wykonania załączonych w tym raporcie rysunków. Jest to funkcja
CharRT32(F) = U(0.1,0.75,π F). Tu i dalej w tym dokumencie
na β będziemy przyjmować wartość 0.75, co odpowiada 12 decybelowemu
[20lg(1 – 0.75)] osłabieniu oświetlenia na skraju czaszy.
function CharRT32(F)
c Napieciowa charakterystyka teleskopu Cassegraina z parabolicznym
c oswietleniem (typu: 1 - beta*(2r/D)^2, gdzie r - promien, beta=0.75)
c i stosunkiem srednic zwierciadel d/D = d_D = 0.1 na czestosci
c przestrzennej F = z/pi = D*q [w cyklach na aperturze D]
data pi/3.1415927/,d_D/0.1/,beta/0.75/
c Znormalizowana charakterystyka teleskopu bez lustra wtornego:
char(b,z) = 4*((1-b)*Bessj1(z) + 2*b*Bessj(2,z)/z)/z/(2-b)
z = max(pi*abs(F),1e-6) ! max, by uniknac dzielenia przez zero
zs = z*d_D
dish = char(beta,z) ! charakterystyka teleskopu bez subrefl.
betas = beta*d_D**2 ! beta na skraju subreflektora
subr = char(betas,zs) ! charakt. teleskopu o srednicy d (subrefl.)
c Czesc calkowitego napiecia przypadajaca na subreflektor:
u = d_D**2*(2 - betas)/(2 - beta)
CharRT32 = (dish - u*subr)/(1 - u)
end |
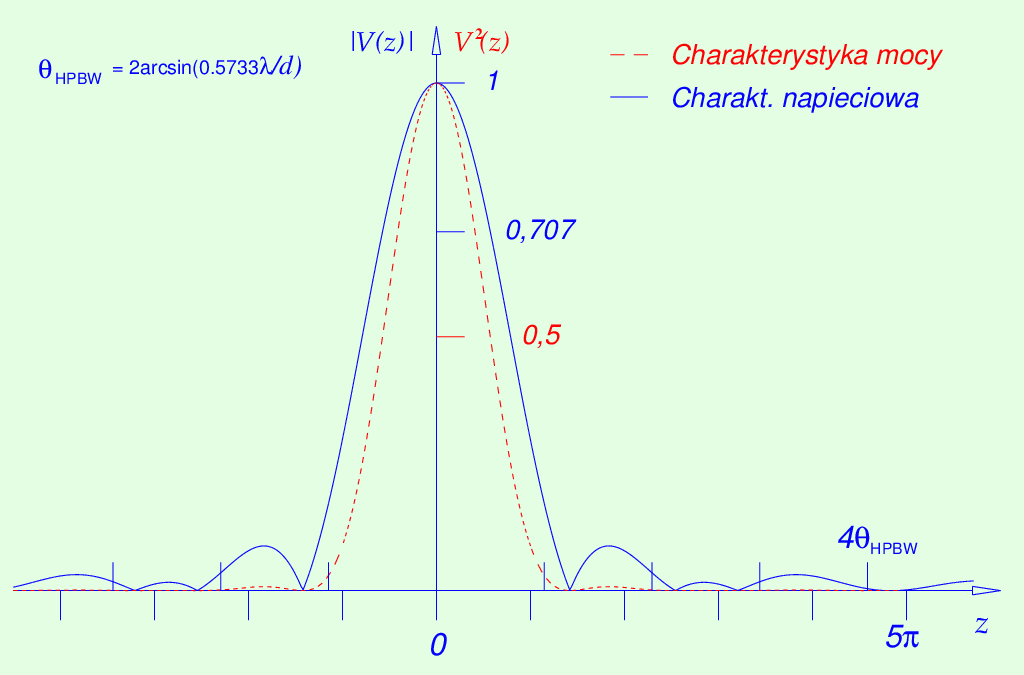
Wykres znormalizowanych funkcji |U| oraz
U2
dla d/D = 0.1 i β = 0.75 [tutaj V(z) = U(0.1,0.75,z)]
(Plot of the normalized voltage and
power pattern functions)
Z teorii anten wiadomo, że jeżeli w argumencie charakterystyki
z = πDq średnicę D wyrazimy w długościach fali,
λ, to q jest kosinusem kierunkowym (kosinusem
kąta między kierunkiem na niebie a płaszczyzną apertury). Argument ten
możemy zatem wyrazić w funkcji kąta θ liczonego
od kierunku maksimum wzmocnienia (prostopadłego do płaszczyzny apertury):
gdzie λ jest długością fali obserwowanego
promieniowania. Dysponując funkcją typu charRT32 łatwo teraz
obliczać kierunkową charakterystykę mocy (kwadrat charakterystyki
napięciowej) w funkcji kąta θ.
W Fortranie kod może mieć np. postać prostej statement function:
char2(theta)=chaRT32(D_lambda*sin(theta))**2 |
gdzie theta = θ
oraz D_lambda =
D/λ.
Poniższe trzy rysunki przedstawiają przestrzenny wygląd charakterystyki
radioteleskopu o aperturze kołowej o średnicy D = 32 m z centralnym otworem
(cień lustra Cassegraina) o średnicy 3.2 m we współrzędnych kątowych
obliczonych dla częstości
5 GHz (λ = 6 cm) i przy oświetleniu z parametrem
β równym 0.75. Rysunki obejmują kwadratowe
pole o boku 148' w pobliżu maksimum wzmocnienia. Na rysunkach zaznaczono
(innym kolorem) również
pełne (niezacienione) przekroje przez maksimum charakterystyki. Charakterystyki
mocy promieniowania zostały przeskalowane w amplitudzie o czynniki ok. 50 i
ok. 4000 w stosunku do charakterystyki napięciowej, by pokazać strukturę
bardzo słabych listków bocznych.
Teoretyczna charakterystyka napięciowa
RT32 (Voltage pattern)
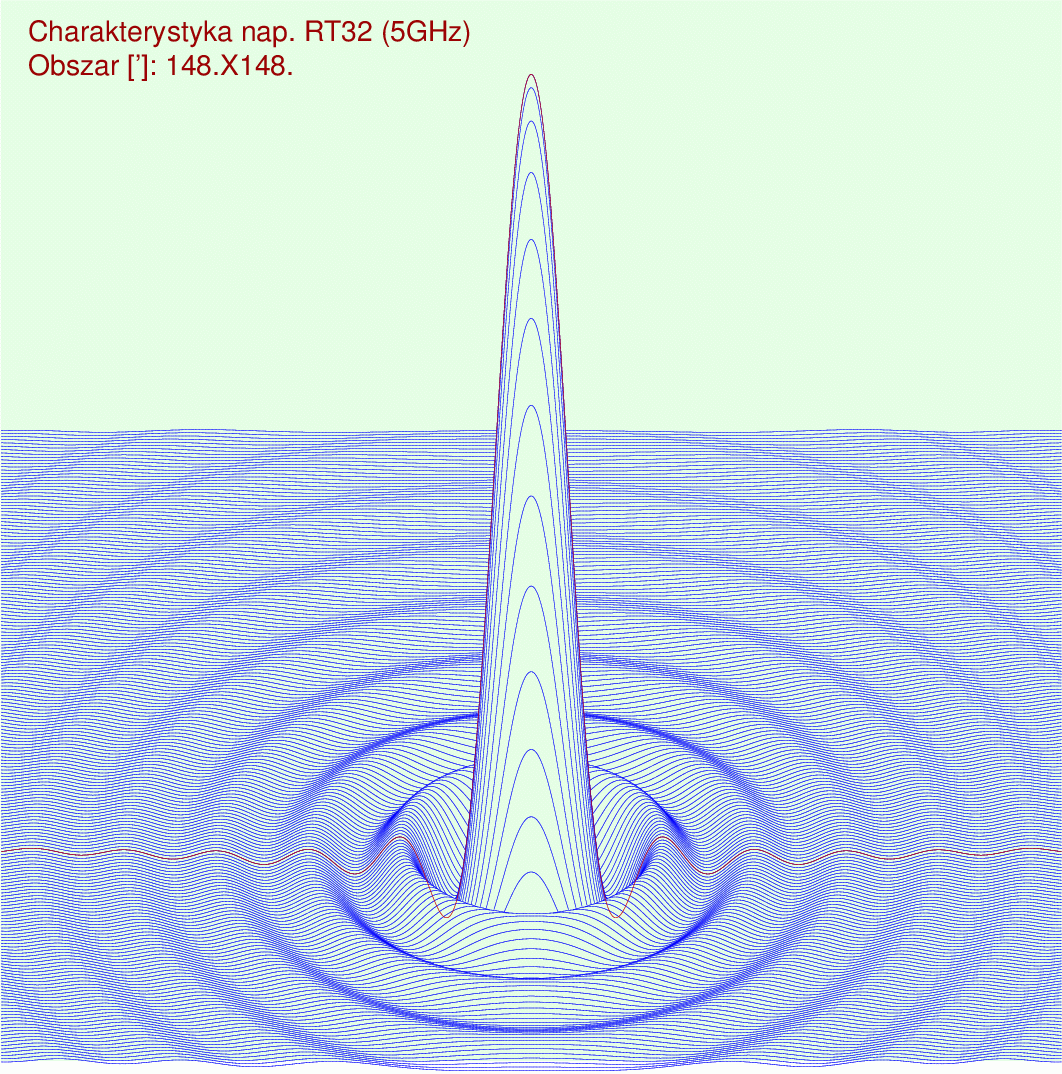
Teoretyczna kierunkowa charakterystyka
promieniowania RT32 (Power pattern)
Najwyższy pierścień wokół obciętej wiązki głównej, czyli pierwszy
listek boczny,
jest ok. 130 razy niższy od maksimum tej wiązki.
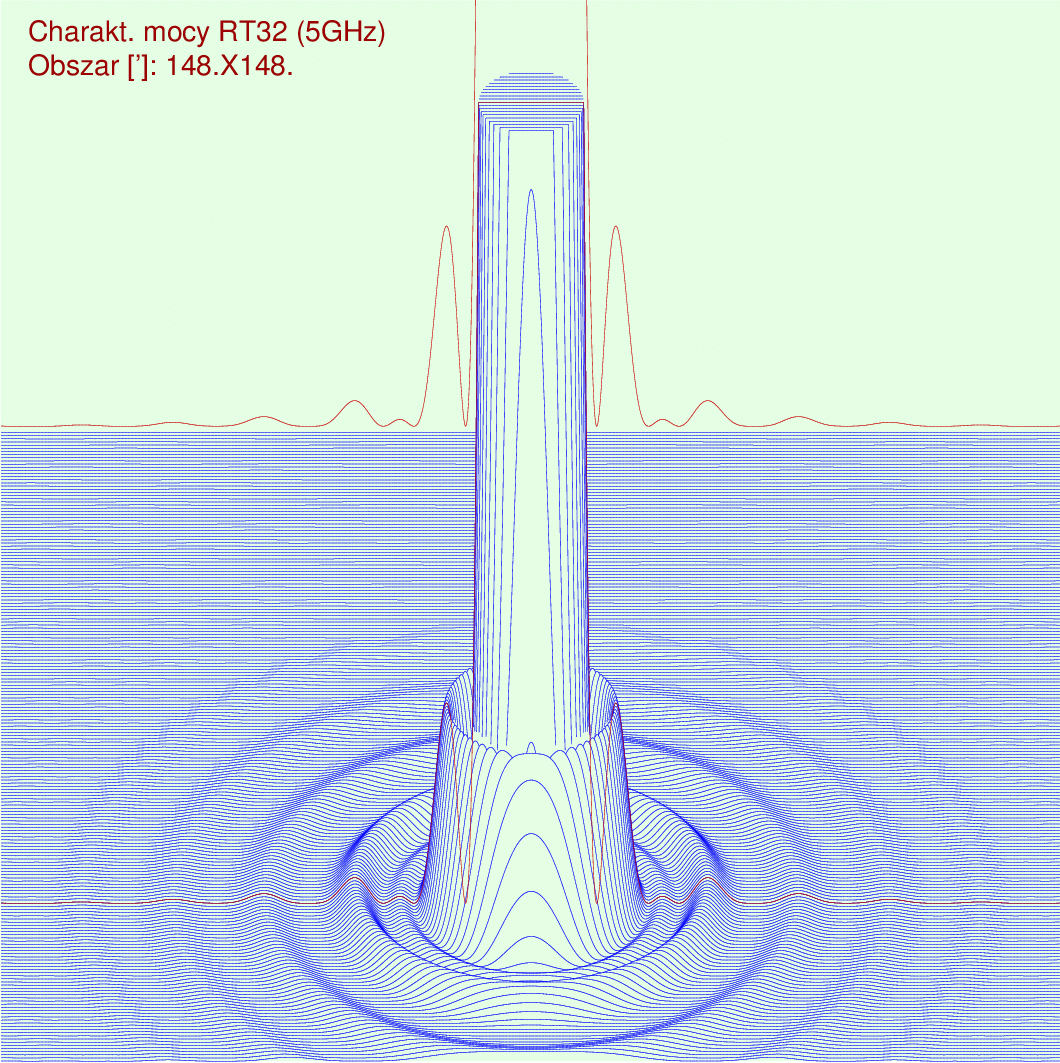
Ta sama charakterystyka mocy
przeskalowana o czynnik 80 (Same pattern shifted and rescaled for details)

|
Numerycznie wyznaczone położenia i poziomy ekstremów charakterystyki
kierunkowej RT32
W pierwszej kolumnie tabeli (Nr) widnieją numery
kolejnych listków bocznych; 'min' oznacza minimum między listkami;
wiersz oznaczony '1/2' zawiera dane o poziomie połowy mocy głównej wiązki;
kąty θ odpowiadające argumentowi z podano
w minutach łuku w siedmiu ostatnich kolumnach, każda dla innej częstości
wymienionej w główce tabeli.
|
Nr z/π Moc Kąty θ ['] na poszczególnych częstościach [GHz]
*108 1.42 1.66 5 11.7 22 30 100
1/2 0.57328 50000000 13.0 11.1 3.7 1.58 0.84 0.62 0.18
min 1.42119 0.0 32.2 27.6 9.2 3.91 2.08 1.53 0.46
1 1.83478 774809.4 41.6 35.6 11.8 5.05 2.69 1.97 0.59
min 2.54375 0.0 57.7 49.4 16.4 7.00 3.72 2.73 0.82
2 2.84691 26630.2 64.6 55.2 18.3 7.84 4.17 3.06 0.92
min 3.20613 0.0 72.7 62.2 20.7 8.83 4.69 3.44 1.03
3 3.82671 99067.6 86.8 74.2 24.6 10.53 5.60 4.11 1.23
min 4.77976 0.0 108.4 92.7 30.8 13.16 7.00 5.13 1.54
4 5.02723 355.6 114.0 97.5 32.4 13.84 7.36 5.40 1.62
min 4.89273 0.0 111.0 94.9 31.5 13.47 7.16 5.25 1.58
5 5.79475 37143.7 131.5 112.4 37.3 15.95 8.48 6.22 1.87
min 6.83215 258.9 155.0 132.6 44.0 18.81 10.00 7.33 2.20
6 7.76764 15231.7 176.3 150.8 50.0 21.38 11.37 8.34 2.50
min 8.83277 9.5 200.4 171.4 56.9 24.31 12.93 9.48 2.84
7 9.74959 5211.5 221.3 189.3 62.8 26.84 14.27 10.47 3.14
min 10.51516 0.0 238.7 204.1 67.7 28.95 15.39 11.29 3.39
8 10.82980 262.6 245.8 210.2 69.8 29.81 15.85 11.63 3.49
min 11.17259 0.0 253.6 216.9 72.0 30.76 16.36 11.99 3.60
9 11.74393 1179.4 266.6 228.0 75.7 32.33 17.19 12.61 3.78
min 12.28627 0.0 279.0 238.6 79.1 33.82 17.99 13.19 3.96
10 12.81732 1007.0 291.1 248.9 82.6 35.28 18.76 13.76 4.13
min 13.44556 0.0 305.4 261.1 86.6 37.01 19.68 14.43 4.33
11 13.75137 95.0 312.3 267.1 88.6 37.85 20.13 14.76 4.43
min 14.05493 0.0 319.2 273.0 90.5 38.69 20.58 15.09 4.53
|
Jednym z ważniejszych parametrów charakterystyki promieniowania
radioteleskopu jest szerokość połówkowa głównej wiązki
θHPBW,
tj. podwojona wartość kąta θ, przy którym
funkcja U maleje do
√{0.5} ≈ 0.707 wartości w maksimum. Przekształcając
(6) otrzymujemy:
|
θHPBW = 2 arcsin |
( |
zHPBW
π |
λ
D
|
) |
. |
|
W przypadku RT32 z obliczeń numerycznych wynika, że
zHPBW = 0.573281 π.
To wyznaczenie pozwala obliczać spodziewane rozdzielczości kątowe RT32 dla
różnych częstości. W poniższej tabelce zebrano przykładowe wyliczenia
Θ =
θHPBW
dla kilku praktycznie użytecznych częstości
(f = c/λ, gdzie c – prędkość światła).
f [MHz] 327 408 610 1420 1660 2290 5000 11700 22000 30000 100000
λ [cm] 91.68 73.48 49.15 21.11 18.06 13.09 5.996 2.562 1.363 0.999 0.300
Θ ['] 112.9 90.51 60.54 26.01 22.25 16.13 7.385 3.156 1.678 1.231 0.369
Θ [°] 1.88 1.51 1.01 0.433 0.371 0.269 0.123 0.053 0.028 0.021 0.006
Δ/1000 11 17 37 200 274 521 2490 13600 48100 89500 994000 |
Parametr w ostatnim wierszu tej tabelki jest kierunkowością teleskopu wyrażoną
w tysiącach. Zdefiniowano ją jako
Δ = 4π/Ω
= 4πU2(0)/[2π∫U2(θ)sinθ dθ],
gdzie całkowanie zostało przeprowadzone w zakresie
0 < θ < π/2.
Otrzymany z tego całkowania kąt bryłowy jest też miarą powierzchni
skutecznej teleskopu, Aeff
= λ2/Ω:
Aeff = 711.27 m2.
Liczba ta naturalnie odzwierciedla jedynie straty powierzchni wynikające
z przesłaniania subreflektorem i z nierównomiernego oświetlenia apertury.
Samo nierównomierne oświetlenie w założonej postaci wnosi straty:
804.25 – (711.27 + 8.0425) = 84.9375 m2, tj. 100*84.9375/804.25 =
10.56 % apertury.
— KMB
Toruń, 2012.06.27 (w pierwotnej formie 19 III 2003 r.)